Horadam四元數關于二項式和的若干恒等式

陳慶華

（福建師范大學 數學與信息學院，福建 福州 350108）

四元數序列是一個數字延伸到復數的數域，其在許多領域分支發揮著重要的作用，如廣泛應用于量子物理和數學等.其中，通過特殊整數序列定義的四元數序列引起了廣泛學者的研究.此外，二項式定理作為初等數學的一個重要定理，是一塊非常熱門的研究內容，其在組合理論、開高次方、高階等差數列求和以及差分法中都有廣泛的應用.本文將四元數與二項式定理結合，探討四元數關于二項式和的有趣的恒等式，不僅是對四元數性質的擴充，也是將二項式和運用到四元數領域，對二項式定理的應用實例研究具有實際意義，凸顯了數學中相關領域的聯系和交叉.

1 Horadam 四元數的介紹

四元數序列是一個數字延伸到復數的數域，它是由實部a0，a1，a2，a3和基1，i，j，k 組成的以下形式的元素：

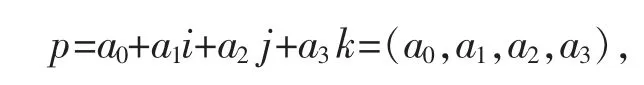
其中i2=j2=k2=-1,ij=k=-ji，jk=i=-kj，ki=j=-ik.

1963年，Horadam[1]定義了系數為Fibonacci 序列和Lucas 序列的四元數

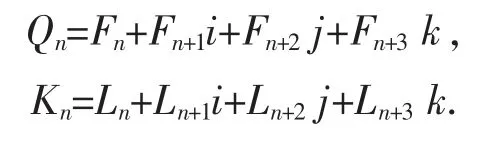
之后，Pell-Lucas 四元數，Jacobsthal-Lucas 四元數等也被學者們廣泛研究.例如，Halici[2]中研究了Fibonacci 和Lucas 四元數的生成函數，Binet 公式和一些組合性質.Ramiz[3]中定義了k-Fibonacci 和k-Lucas 四元數，并得出類似于Cassini 恒等式的一些公式，此外，文獻[4]引入了h(x)-Fibonacci 四元數多項式，推廣了k-Fibonacci 四元數，更多關于四元數的內容可參考文獻[5-8].

近年來，Serpil 等[9]推廣了一種新的四元數序列，即Horadam 四元數.包含了前人所研究的四元數序列，如Fibonacci 四元數、Lucas 四元數、Pell-Lucas 四元數、Jacobsthal-Lucas 四元數.

定義1Horadam 四元數被定義為：

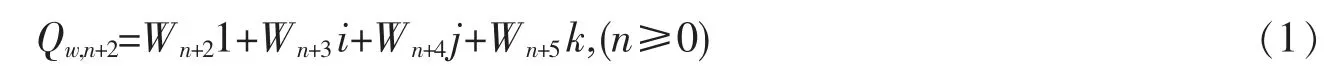
這里Wn是第n 個Horadam 數，其通項公式表示為：

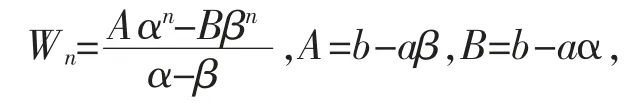
且這個四元數符合如下遞推關系：

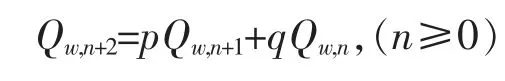
該遞推關系的特征方程的根為：

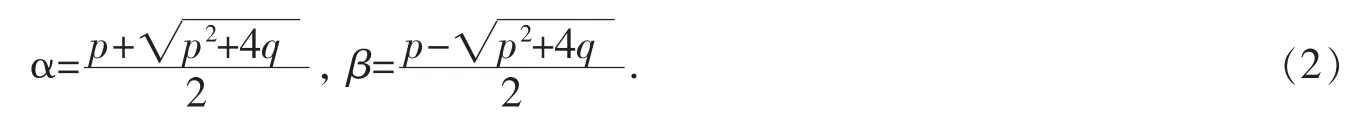
令Δ=p2+4q，即α-β=，得到：

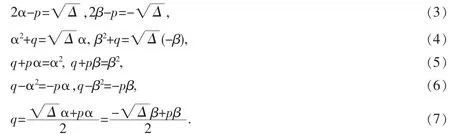
引理1Horadam 四元數的Binet 公式表示為：

基于這些研究，本文推導出Horadam 四元數的一些恒等式.本文第2 節介紹了Horadam 四元數的指生成數型函數.第3 節推導出這個Horadam 四元數關于二項式和的一些恒等式，推廣了對二項式定理的應用.

2 關于Horadam 四元數的結論

2.1 Horadam 四元數的指數型生成函數

不同于普通的生成函數，推導出Horadam 四元數的指數型的生成函數.

定理1Horadam 四元數的指數型生成函數為：

證明將式(8)代入式（9）左邊得由于，因此有，定理得證.

2.2 Horadam 四元數關于二項式和的恒等式

這一部分得出若干關于二項式和的恒等式.首先，回顧二項式系數（）定義為：

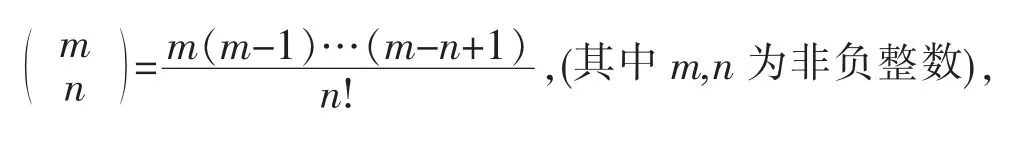
定理2令n 為非負整數，則

定理3令n 為非負整數，則

證明將式(8)代入式（11）左邊得

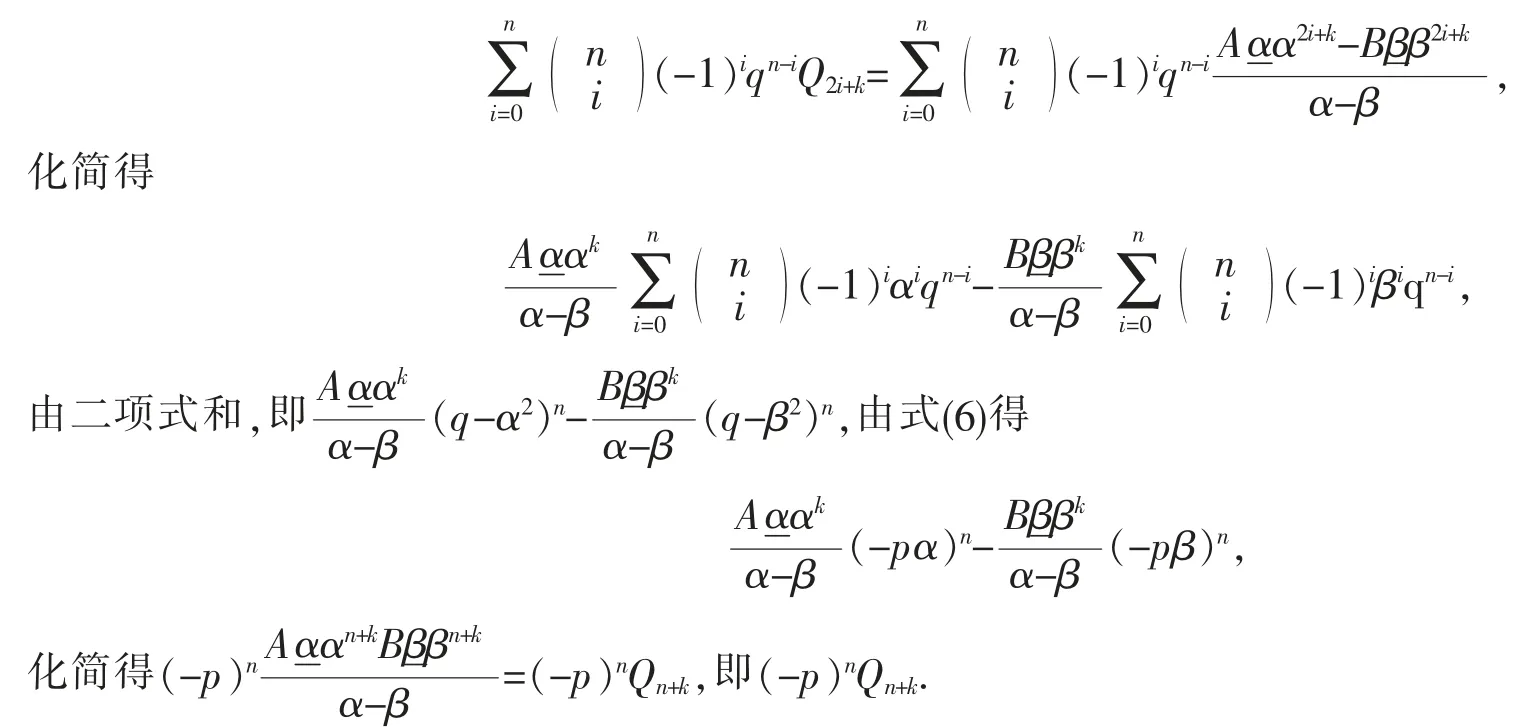
定理4令n 為非負整數，則

證明將式(8)代入式（12）左邊得

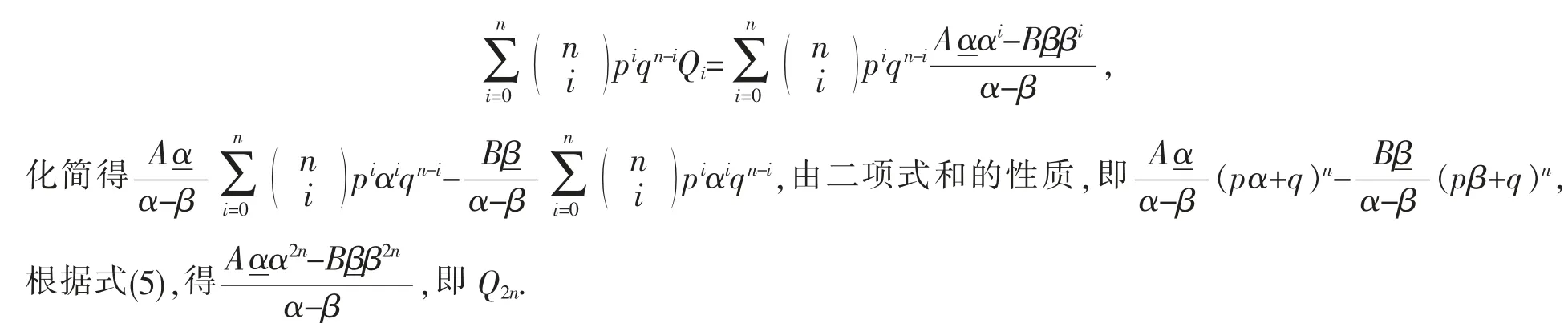
定理5令n 為非負整數，則

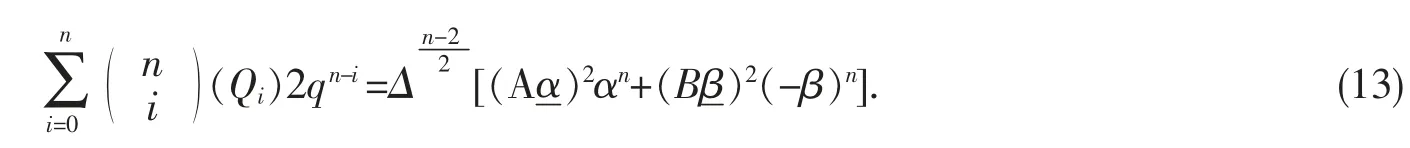
證明將式（8）代入式（13）左邊得

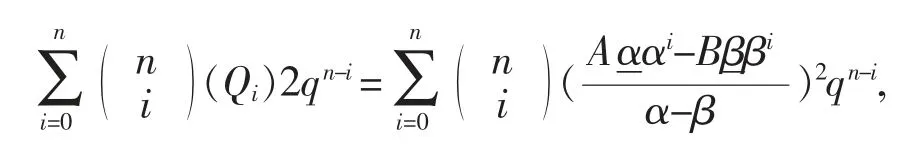
已知(α-β)2=Δ，且四元數不滿足乘法交換律，化簡得

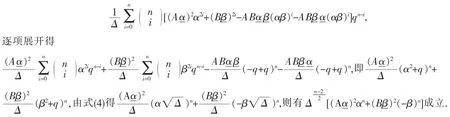
注1若取a=0，b=1，則定理1-5 為文獻[10]中的特殊情況.

定理6令n 為非負整數，則

證明將式(8)代入式（14）左邊得

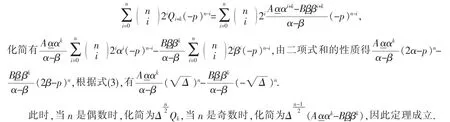
定理7令n 為非負整數，則

證明將式(8)代入式（15）左邊得

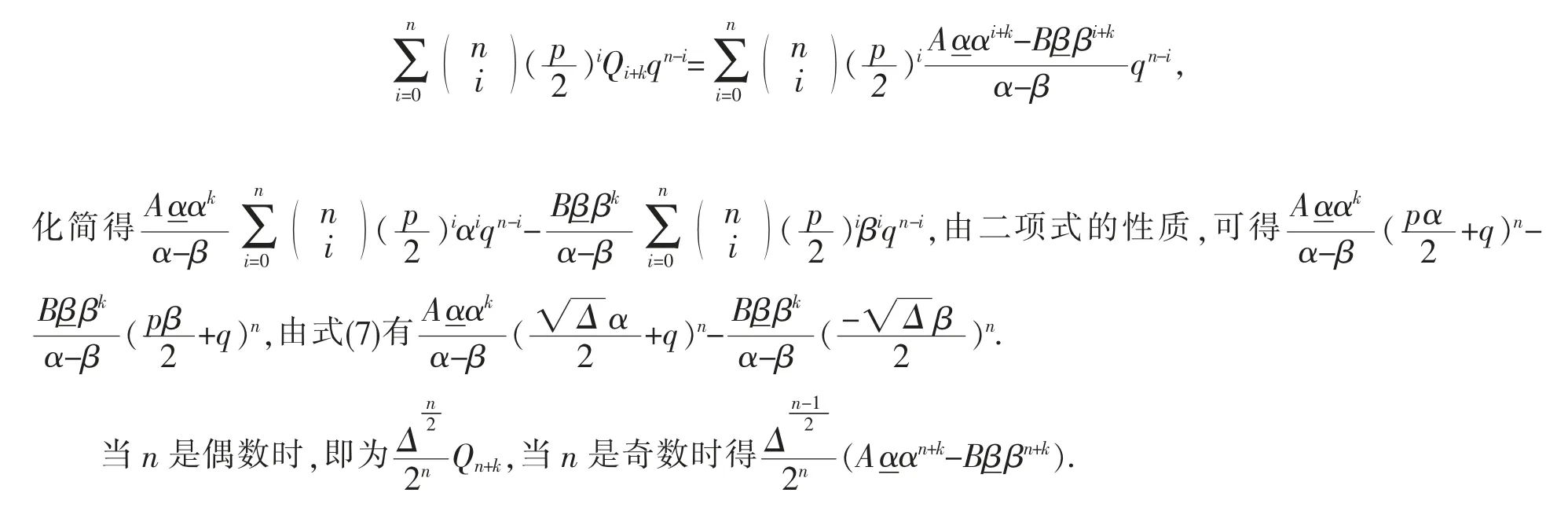
3 總論

本文從特殊的四元數序列，即Horadam 四元數出發，先計算指數型生成函數，其次把二項式和與四元數結合，推導得出若干恒等式，使四元數的性質更加豐富，推廣了二項式定理的應用.