基于柯西型K-積分性質及其應用探討
2021-04-11 05:43:50孟紅軍
紅河學院學報 2021年2期
孟紅軍
(滁州城市職業學院教育系,安徽滁州 239000)
復變函數論是高等數學的重要組成部分。它主要包括單值解析函數理論、黎曼曲面理論、幾何函數論、留數理論、廣義解析函數理論等方面的內容。復變函數論中仍然有不少尚待研究的課題,它將繼續向前發展,并將取得更多研究成果。肖卓峰等[1]提出來通過Clifford分析方法的廣義坐標變換,利用密度行數來測算積分算子的模式。杜爭光等[2]提出利用Beta積分的方式對柯西中值定理進行探討,并確立了定理的漸進性。陳雪等[3]提出利用函數的柯西積分性質來分析柯西積分公式。基于此,可以看出通過復積分的方式研究解析函數,在復積分的研究過程中,延伸出了很多重要的知識。利用柯西型K-積分的相關性質進行研究,可以得到復變函數積分的相關性質在復變函數K-積分中的應用。
1 柯西型K-積分的連續性與解析性
1.1 柯西型K積分的相關定義


1.2 相關引理

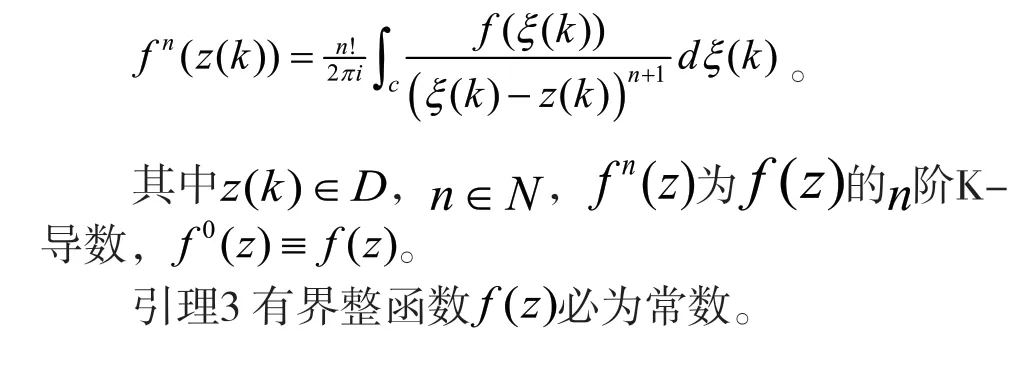
2 柯西型K-積分的連續性、解析性及證明
2.1 定理1證明

2.2 定理2證明

3 柯西型K-積分的相關性質證明
3.1 定理3證明

證:分別作圓心為和的充分小的圓周(如圖1)。
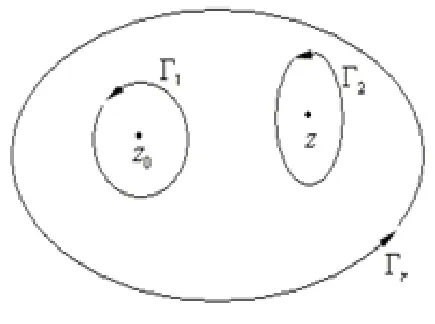
圖1 充分小的圓周,

3.2 定理4證明

3.3 定理5證明



3.4 定理6證明


4 結論
主要研究了柯西型K-積分的相關性質。對柯西積分和柯西型積分、柯西K-積分和柯西型K-積分的區別和聯系做出了簡單的介紹,指出柯西積分(K-積分)是柯西型積分(K-積分)的特例,而柯西型積分(K-積分)就不一定為柯西積分(K-積分)。只有當在上解析(或K-解析)時,柯西型積分(K-積分)才是柯西積分(K-積分)。
首先對柯西型K-積分的連續性和解析性進行討論并證明,然后又對一定條件下的柯西型K-積分的一些相關性質進行討論和證明。研究發現,柯西型K-積分的相關性質是柯西型積分的相關性質在K-積分中的應用,該結論是對復變函數K-積分理論的補充。
猜你喜歡
體育科技文獻通報(2022年3期)2022-05-23 13:46:54
當代陜西(2022年5期)2022-04-19 12:10:18
新世紀智能(數學備考)(2021年9期)2021-11-24 01:14:28
遼金歷史與考古(2021年0期)2021-07-29 01:06:54
中學生數理化(高中版.高二數學)(2021年5期)2021-07-21 02:14:46
湘潮(上半月)(2021年4期)2021-07-20 08:05:28
汕頭大學學報(自然科學版)(2020年4期)2020-12-14 07:05:00
中等數學(2020年6期)2020-09-21 09:32:38
科技傳播(2019年22期)2020-01-14 03:06:54
中等數學(2019年6期)2019-08-30 03:41:46

