基于阻力和伴流不均勻度的多用途船型線優化

魏斯行，馬 寧，顧解忡，王 楠，陸明鋒

(1.上海交通大學海洋工程國家重點實驗室，上海200240；2.上海交通大學船舶海洋與建筑工程學院，上海200240；3.高新船舶與深海開發裝備協同創新中心，上海200240；4.南通中遠海運川崎船舶工程有限公司，江蘇南通226000)

0 引 言

多用途船以其分艙靈活的特點，正逐步成為除集裝箱船、油船和散貨船三大主流船型以外的第4種主流船型。因此針對多用途船進行型線優化設計，以改善多用途船的阻力性能，對節能降耗和增加營運效益來說都具有重要意義。傳統的型線設計模式主要依賴設計經驗以及船舶型線數據庫，耗時耗力，且方案非最優。而近些年提出的SBD(Simulation Based Design)技術，則是結合了最優化技術以及計算流體動力學，使得整個型線設計流程更加高效。

近十幾年來，國內外船型優化尤其在以阻力最優為目標的船體型線優化方面得到了迅猛的發展，主要工作集中在對中高速船的船首或船的中前部型線進行優化，并獲得了較好的減阻效果[1–3]。而對于低速肥大型船舶而言，相較于阻力性能，其尾部流場的品質也越來越受到設計研究者的重視[4–5]。

本文以某低速肥大型的多用途船為研究目標，以其阻力以及伴流場不均勻度為優化目標，通過RBF插值方法實現船體曲面變形，進而采用Shipflow軟件計算船舶的總阻力和伴流場不均勻度，結合非劣分類遺傳算法以及Kriging代理模型快速求解得到性能最優的型線，并通過STAR CCM+對優化結果進行驗證，根據優化結果為該多用途船提出了首尾型線趨勢性建議。

1 船體型線優化

1.1 優化目標

以某多用途船作為研究對象，分別考慮船首和船尾形狀改變對船舶水動力性能的影響。優化工況選取設計航速13.77 kn，吃水11m。船首形狀改變主要影響興波阻力，因此以興波阻力為優化目標；船尾型線優化時，則以總阻力和伴流場不均勻度為優化目標。該船的主尺度信息以及優化時的約束條件見表1。

表1 多用途船參數及約束條件Tab.1 Parameters and restrictions of multipurpose ship

1.2 船體曲面變形方法

基于徑向基函數[6]（RBF）的曲面變形方法屬于船體曲面局部變形方法，該方法主要通過局部控制點的位移實現船體曲面的變形，并保證變形后船體曲面的連續性與光滑性。

船體表面節點的位移可以通過插值函數S(x)描述，其中x=(xj,yj,zj)為船體表面網格節點。插值函數S(x)有如下表述:

式中：xj=(xj,yj,zj) 為徑向基函數中心；p(x)為多項式；N為控制點的個數； ‖x‖表 示歐式距離；?為對應于歐氏距離的徑向基函數。本文選用W end land's方程，其具有2階連續性：

p(x)

式中：多項式 在本文中采用線性多項式以實現旋轉平移，即

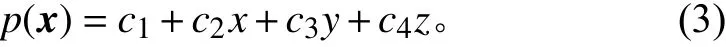
基于上述方法，為了實現船首和船尾的變形，首先需要對可變控制點進行布置。布置的原則是可變控制點可以使得首尾形狀UV度在一個較大的范圍內變化，對于船首型線，可變控制點應該布置在船首的進流段，對于船尾型線，應該布置在船尾的去流段，所有可變控制點的變化方向均為Y方向。為了保證船中型線不受影響，還應在船中部分添加固定控制點。具體布置情況見圖1，可變控制點的詳細布置信息見表2。

圖1 可變控制點的位置Fig.1 Location of variable control points

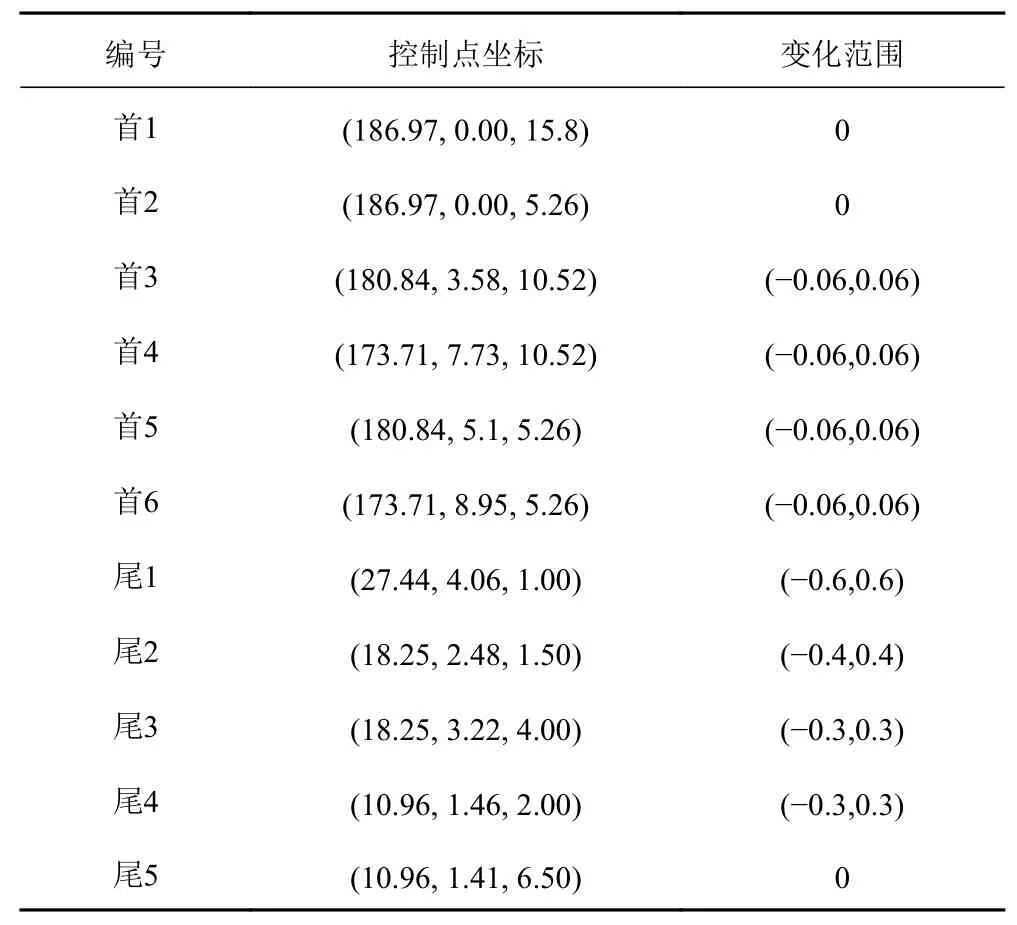
表2 可變控制點的參數Tab.2 Parametersof variable control points

1.3 阻力和伴流場計算方法

圖2 Shipflow計算區域劃分Fig.2 Computational domain in Shipflow

借助流體力學分析軟件Shipflow進行水動力性能快速計算。該軟件對不同的阻力成分，在計算和分析時會采用不同的理論模型：對于興波阻力，計算時采用Rankine源非線性勢流理論方法（船體表面壓力積分和船尾能量法）；對于摩擦阻力，采用邊界層動量積分方法進行求解；對于低速肥大型船中占總阻力成分較小的粘壓阻力，計算分析時采用k?ε湍流模型來求解RANS方程，計算域從船體中部開始。不同方法的計算域劃分如圖2所示。Shipflow通過對不同阻力成分進行分區計算，雖然可以大大縮短計算周期，但和完全基于RANS方程求解的CFD方法相比，計算精度卻下降了。表3為該多用途船的阻力性能實驗結果與Shipflow計算結果和完全基于RANS方法的流體力學計算軟件STAR CCM+的計算結果對比。Shipflow對于總阻力的預報結果誤差在5%左右，STAR CCM+的精度則更高，誤差僅有0.51%。因此，對于船型優化來說，可以采用預報時間更短的Shipflow計算船舶水動力性能，采用預報精度更高的STAR CCM+來驗證優化結果的可靠性。

表3 多用途船阻力數值計算值與試驗結果對比Tab.3 Comparison between numerical simulation and test results of resistanceof multipurpose ship

對于多用途船的尾部伴流品質的評估，本文采用的是荷蘭MARIN水池提出的伴流目標函數WOF(wake object function)[7]。WOF越小說明伴流越均勻，反之則均勻性越差。WOF的計算公式如下：

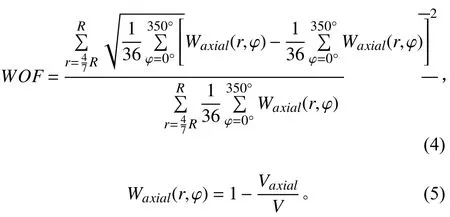
其中：R為螺旋槳半徑；φ值為0°～350°，間隔10°；Vaxial為水流軸向速度。

1.4 優化算法

采用帶精英策略的非支配排序遺傳算法NSGA-II[8]在設計空間搜索滿足排水量約束條件的最優船型。考慮到時間成本與計算精度，船首優化時選取的初始種群個體數為30，迭代次數設置為30；船尾優化時選取的初始種群個體數為50，迭代次數設置為50。

2 Kriging近似模型

通過引入代理模型，可以解決船型優化中傳統CFD計算耗時的問題。首先通過拉丁超立方采樣方法[9]，生成100個樣本集作為輸入值；然后使用Ship flow對這些樣本點所對應的船型進行水動力性能計算，計算結果作為輸出值；最后利用這些輸入輸出值構造Kriging近似模型，并驗證近似模型的可信度。

圖3 為尾部控制點變量1（Y1）和變量2（Y2）在取值范圍內的分布，可以觀察到變量是隨機且均勻分布在取值范圍內的。

圖3 部分變量在二維空間投影Fig.3 Projection of part of variables

K riging[10]代理模型對于待測點的響應預測值表達如下：

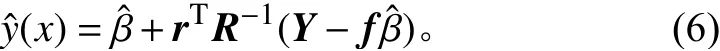
其中：Y為由n個樣本點所組成的n維列向量；f為常值列向量，其元素全部為1；R為n階對稱方陣，其元素為表示任意2個樣本點 (xi,xj)之間空間相關性的相關函數R(xi,xj)；β?為回歸模型參數；r為待測點和樣本點(x,xi) 之間空間相關性相關函數R(xi,xj)所組成的n維向量。

圖4 顯示了船首優化時，K riging模型響應預測值與實際CFD計算結果的對比，同時計算兩者的均方根誤差可以得到RMS=0.0176。可以看出，兩者結果吻合良好。該代理模型可用于船型優化。

3 優化結果分析

3.1 首部型線優化結果

興波阻力對船首形狀變化敏感，因此將興波阻力設為船首優化的目標函數。船首優化過程中興波阻力優化迭代歷程如圖5所示。可以看出，船舶興波阻力在迭代的過程中逐步地減小并逐步收斂至一穩定值。圖6為多用途船船首優化前后船側的波切圖對比，可以觀察到優化船在靠近船首的第一個波谷值的峰值有所下降，這是興波阻力得到改善的原因。

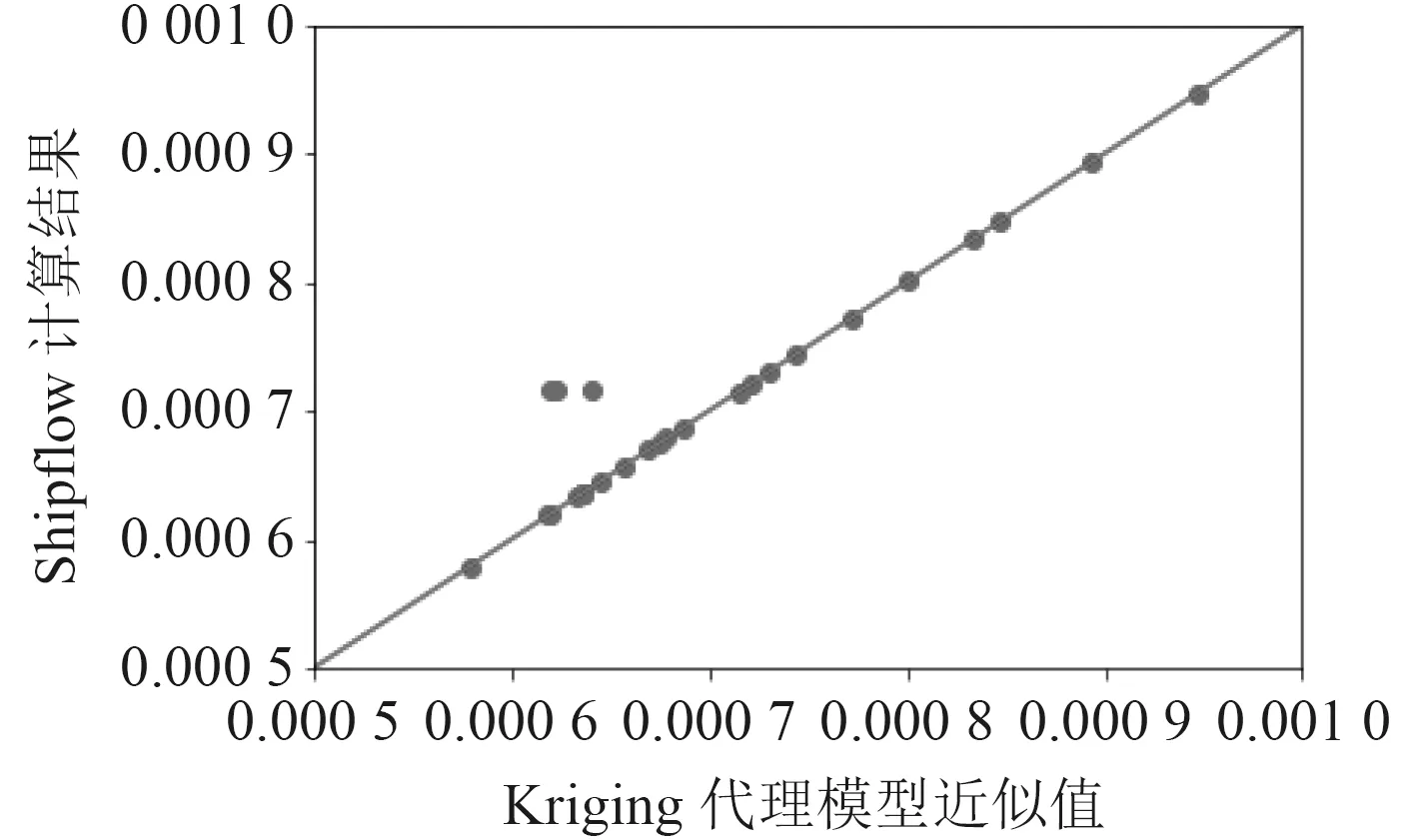
圖4 Kriging近似模型預測值與CFD計算值結果對比Fig. 4 Comparison between Kriging approximation model predictive valueand CFD results

圖5 興波阻力優化迭代歷程Fig.5 Iteration process of wave resistance coefficient

圖6 船首優化前后波切圖對比Fig. 6 Comparison of wave cut profile before and after bow optim ization

根據最終的Pareto解，得到4個可變控制點的變化值，從而得到了優化后的型線。通過對新的型線重新建模，并在高精度的CFD求解器STAR CCM+中進行驗證，驗證后的阻力成分對比見表4。結果顯示，阻力優化趨勢與Shipflow中的計算結果基本一致，其中剩余阻力減少2.47%，摩擦阻力減少0.37%，總阻力減少0.80%。

表4 船首優化結果的STAR CCM+驗證Tab.4 STAR CCM +verification of bow optimization results

船舶型線的變化如圖7所示。從型線變化的趨勢來看，船首橫剖線的形狀由U型過渡為V型，V型船首較于U型船首濕面積小，因此可減小摩擦阻力。同時V型艏水下部分較瘦，易于使水流沿著縱剖線方向流動，從而減少舭部產生的旋渦，所以對剩余阻力性能也是有利的。

圖7 船首優化前后橫剖線對比Fig.7 Cross-section lines beforeand after bow optim ization

因此對該多用途船來說，在保證排水量前提下，為了獲得更好的阻力性能，首部橫剖線形狀應該更趨向于V型。

3.2 尾部型線優化結果

船尾形狀改變主要影響船舶粘性阻力以及尾部伴流場，因此船尾優化時以總阻力以及槳盤處伴流不均勻度作為優化目標。船尾優化過程中船舶總阻力與槳盤面伴流不均勻度迭代歷程如圖8所示。從優化結果上來看，船尾型線變化導致總阻力和艉部伴流場變化，且總體上呈現負相關的趨勢，即船舶總阻力越小，伴流不均勻度越大。

圖8 船尾優化結果Pareto解集Fig.8 Pareto solution of Stern optim ization result

從圖8 Pareto解集中挑選出2組具有代表性的解，對K riging近似模型得到的優化結果進行驗證，通過Shipflow計算結果見表5?？梢杂^察到，當尾流場不均勻度大大減少了近29%時（opt1），船舶總阻力卻增加了4.27%，這顯然不是希望得到的優化船型。而方案opt2中的WOF值減小23.53%，同時總阻力也減小了2.79%。因此選擇op t2中的優化船舶進行模型重建，并在STAR CCM+中進行驗證。

STAR CCM+驗證后的阻力成分對比如表6所示。結果顯示，船舶總阻力增加了0.89%，其中剩余阻力增加了5%左右，摩擦阻力減少了0.16%。這說明船舶阻力的改變主要是因為剩余阻力的變化引起的。

船舶型線的變化如圖9所示。從優化結果來看，船尾型線在接近推進器時，形狀逐漸由V型朝著U型變化。圖10為尾部型線優化前后槳盤處速度云圖。原始船V型尾的存在使得船底下部的流體順著船體舭部流向螺旋槳盤面，由于邊界層的影響，在螺旋槳盤面的中心垂直平面易形成高伴流區；優化船所對應的U型尾，在靠近尾軸處上方型線呈現“內凹”狀，船尾舭部半徑變小，因此水流在舭部更容易發生邊界層分離，形成舭渦，從而削弱了槳盤面上部產生的伴流峰值，從而使得伴流場均勻性得到改善。但由于舭渦的存在會造成能量損失，因此優化船的粘壓阻力較之前會有所增大。這正是優化船槳盤面處不均勻度得到改善，但總阻力有所增大的原因。

表5 優化方案及總阻力與伴流不均勻度變化Tab.5 Optimization scheme and variation of total resistance and wake non-uniformity

表6 船尾優化結果的STAR CCM+驗證Tab.6 STAR CCM + verification of stern optimization results

圖9 船尾優化前后橫剖線對比Fig.9 Cross-section lines beforeand after stern optimization

圖10 船尾優化前后槳盤面處速度分布對比Fig.10 Velocity distribution at propeller disk before and after stern optim ization

因此對該多用途船來說，為了獲得更均勻伴流場，同時阻力不至于惡化太多，可以使船尾型線在接近推進器時，形狀逐漸由V型朝著U型變化。

4 結語

本文將多用途船作為研究對象，采用徑向基函數插值方法實現船體曲面變形，利用Kriging近似模型替代耗時的CFD計算以提高優化效率，分別對多用途船船首和船尾形狀進行優化。優化結果表明：對于該多用途船船首形狀，采用V型船首可以獲得更好的阻力性能；對于船尾形狀，由于尾部伴流場不均勻度與阻力性能呈現矛盾的關系，因此為了獲得更均勻的伴流場同時阻力不至于惡化太多，可以使船尾橫剖線在接近推進器時，形狀逐漸由V型朝著U型變化。