借助極限思維法巧解高中物理題

周學曄

【摘 要】極限思維法是指運用極限概念分析與解決問題的一種方法。在分析相關問題時應用極限思維可從較為抽象的情境中迅速找到相關規律，找到問題答案。眾所周知，高中物理習題靈活多變，解題時應注重根據題型特點，采用高效的解題思維，尤其是在解答高中物理選擇題時運用極限思維法可獲得事半功倍的效果。教學中為使學生能夠靈活運用極限思維法解答物理習題，既要注重相關理論的教學，又要為學生展示極限思維法的具體應用。

【關鍵詞】極限思維法;高中物理;巧解;習題

應用極限思維法解答高中物理習題時要將某一參數向極限方向考慮，如趨于零、趨向無限大、趨向無限小等，并將其帶入給出的選項中，如在極限情況下選項正確，這個選項也就是正確答案。當然需要注意的是運用極限思維法時，極限情境應滿足題干情境，不能主觀臆斷，盲目地使用極限思維法。

1? ?借助極限思維法，巧解上拋類的習題

運動學是高中物理的重要構成部分，涵蓋的運動類型較多，主要包括勻加速直線運動、平拋運動、圓周運動等。其中，豎直上拋運動屬于勻加速直線運動的特例，物體在上升的過程中受到其自身的重力和空氣阻力的影響，兩者的方向均是豎直向下;在下落的過程中，物體受到的重力向下，受到的空氣阻力向上。一些高中物理習題常以豎直上拋為背景，考查學生對勻加速直線運動的認識與理解程度。解題時應具備靈活的思維，具體問題具體分析，尤其是要借助極限思維法，實現高效解題[1]。如對下題采用極限思維法進行分析，幾乎不需要進行計算便可選出正確答案。

將一物體以初速度 v1 豎直上拋，重新落到拋出點的末速度為 v2 ，且=K，若物體在整個運動過程中受到的空氣阻力f不變，則f和物體所受的重力 G 的大小之比為（? ）。

該題創設的運動情境雖然較為簡單，但分析起來較為抽象。如果采用常規的解題思路，則需要設出一些參數，解題過程較為復雜，不易得出正確結果。而采用極限思維可大大縮短解題時間，即在物體運動的過程中可將空氣的阻力f看做無限接近于零，則，此時K的值趨向于1。考慮到該題為選擇題，因此可將 K = 1 代入四個選項，看哪個選項的值為0。顯然四個選項中只有D項的值為0，因此正確選項為D。

2? ?借助極限思維法，巧解彈簧類的習題

彈簧是高中物理習題中經常出現的事物，其既能考查學生對受力分析知識的掌握情況，又能考查學生對能量方面知識的掌握情況。因彈簧不同的形變會產生不同的力的效果，因此，學生在分析相關問題時常常感覺不知如何入手。為使學生掌握解題的技巧，教學中既要注重運用多媒體技術為學生直觀展示不同形變狀態下彈簧力的情況，使其切實夯實基礎，又要注重為學生講解極限思維法在解題中的應用，不斷鍛煉學生思維的靈活性，使學生在以后遇到類似問題時能夠另辟蹊徑，迅速找到正確答案[2]。如下題：

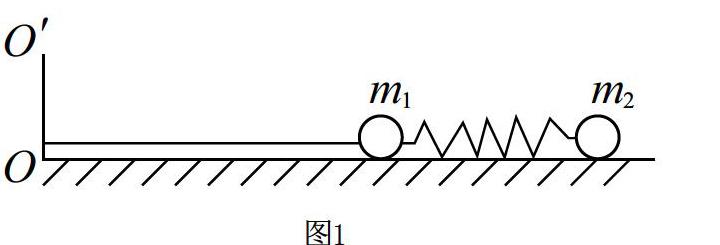
如圖1所示，一輕質彈簧連接兩個小球，小球的質量分別為 m1 、m2 ，并使用一細線 L1 將 m1 連接到 OO' 軸上。若兩個小球均以角速度繞軸在光滑的水平面上轉動，且兩球間的距離為 L2 。若在某一時刻細線突然斷開，則斷開的瞬間兩球的加速度分別為（? ）。

A.a1=L1，a2=（L2+L1），方向相同

B.a1=（L2+L1），a2=（L1+L2），方向相反

C.a1=（L1+L2），a2=L2，方向相反

D.a1=L1，a2=（L1+L2），方向相反

如果采用常規解法，需要分別對 m1 、m2 進行受力分析，再應用圓周運動列出相關的方程，進行計算。這樣雖然能夠得出正確結果，但花費的時間較長，在考試中不可取。而使用極限思維可不用列出方程，結合彈簧的受力特點便能很快找到正確答案。由于兩個小球的質量為 m1 、m2 ，可假設m1 無限趨近于 m2 ，反之亦可。再假設細線斷裂瞬間彈簧兩端的受力大小相等，方向相反，則小球的加速度也應大小相等，方向相反。將 m1 = m2 代入四個選項，發現只有B項滿足兩個小球的加速度相等，因此選擇B項。

3? ?借助極限思維法，巧解電場類的習題

高中物理電場方面的知識較為抽象，學生需要深入理解與掌握相關規律，在解題中才能以不變應萬變。對此，教師應引導學生做好解題思維的積累，尤其應注重結合學生所學設計相關習題，與學生一起分析如何運用極限思維法解答電場類的習題，在深化其對電場知識理解的同時，使其更好地把握運用極限思維法解題的細節以及注意事項，在分析問題時能透過現象看本質，借助極限思維法，迅速破題[3]。如下題：

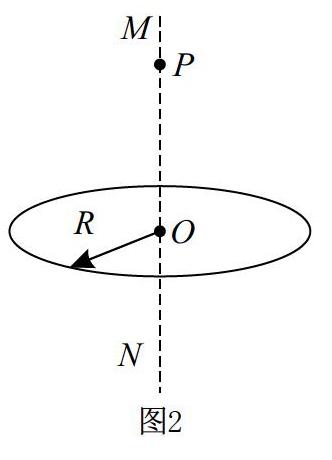
如圖2，一帶正電的圓板半徑為 R ，中心 O 帶有一小孔，水平放置，MN 為過 O 點的豎直軸線。另有一帶正電的微粒由靜止從 P 點釋放，微粒下落穿過 O 點，則從 P 運動至 O 的過程中，以下說法正確的是（? ）。

A.微粒的加速度減小

B.微粒的速度增大

C.微粒的電勢能減小

D.微粒的電勢能先增大后減小

通過認真審題可知， P 點和 O 點的距離并未明確告知，因此需要運用極限思維進行分析。設 P 點和 O 點的距離為 r ，則當 r 趨向于無窮遠時，場強 E 趨向于0。而在 O 點，由對稱性可知，在該點的場強 E =0 ，因此，從 P 點到 O 點的場強可能一直減小，也可能先增大后減小。因微粒剛開始下落，因此其重力大于電場力，則a=，因此 a 可能一直增大，也可能先減小后增大，故A選項錯誤。但其有加速度表明其速度是一直增大的，所以B選項正確。距離正電荷越近，正電荷的電勢能越大，因此C、D兩選項錯誤[4]。

4? ?借助極限思維法，巧解星球類的習題

萬有引力定律是解答行星運動的重要理論。將其與圓周運動知識結合起來，可求解很多的參數[5]。但部分習題采用常規解法并不可取，尤其在測試中會浪費大量時間，因此在教學中應引導學生使用極限思維法求解，尤其是在解答相關選擇題時，應注重應用極限思維法，將不符合實際的選項快速排除[6]。課堂上應注重與學生一起分析如下類型的習題，使學生親身體會極限思維法在解題中的妙用。

將地球看作質量均勻的球體。已知地球表面的重力加速度在兩極的大小為 g0 ，在赤道的大小為 g ，地球自轉的周期為 T ，引力常量為 G ，則地球的密度=（? ）。

很多學生看到該題時應用萬有引力定律，列出相關的方程進行求解，計算較為繁瑣，容易出錯，而使用極限思維法進行簡單的分析便能很快得出正確答案。若地球不自轉，此時 g=g0 ，T 趨向于無窮大。但地球的密度不可能為零。A項，→0，→0，乘積為0，錯誤。B項，→0，→+∞，乘積可能為常數，正確。C項，→0;D項，→0，=1，乘積為0。綜上，B項正確。。

5? ?總結

高中物理教學中為提高學生的解題能力，應從總體上把握教學內容，對基礎知識做好細致深入的講解，同時應注重讓學生掌握極限思維法，優選、精講有代表性的例題，使學生體會到極限思維法在解題中的妙用，養成運用極限思維法解題的意識與習慣。教師還要鼓勵學生在學習上多做總結，真正吃透、理解極限思維法，從而在解題中能夠融會貫通，舉一反三。

【參考文獻】

[1]夏光輝.極限思維法在高中物理教學解題中的應用分析[J].數理化解題研究，2020（28）.

[2]林興貴.極限思維法在高中物理解題中的應用[J].中學生數理化（自主招生），2020（6）.

[3]史洪星.高中物理解題中極限思維法的應用探究[J].數理化解題研究，2020（9）.

[4]管士成.探討極限思維法在高中物理解題中的應用[J].試題與研究，2020（6）.

[5]張甲申.極限思維法在高中物理教學解題中的應用分析[J].高考，2020（4）.

[6]馮翠萍.極限思維法在高中物理教學解題中的應用分析[J].當代教研論叢，2019（11）.

[7]鄭建平.解析高中物理解題中極限思維法的實踐[J].中學生數理化（教與學），2019（10）.