顆粒形態對粗粒土滲透系數影響的數值模擬研究
駱莉莎,周 昕,林 軍
(江蘇開放大學,江蘇 南京,210000)
1 引言
在地下空間開發中,工程降水是必不可少的工程環節;在于土石壩工程、邊坡工程、道路工程中,土體滲流特性也是關系工程穩定性和安全性的關鍵因素。土體滲透系數是描述地下水在土體孔隙中滲流特性的關鍵參數,也是決定工程降水設計的關鍵。目前確定土體滲透系數的方法包括經驗法、室內試驗法,原位抽水試驗法。由于影響
土滲透性的因素非常多,經驗法往往難以準確獲得滲透系數;室內試驗法很難制備與原位場地具有相同微觀結構的土樣,因而試驗結果準確性不夠,而且對于粗粒土試樣必須足夠大,常規試驗設備不滿足要求。原位抽水試驗法是確定現場滲透系數的最可靠方法,然而由于對地下地層結構掌握不全面,地下水連通性無法準確揭示,根據抽水試驗得到的滲透系數也存在影響因素多、準確性無法保證的缺陷。
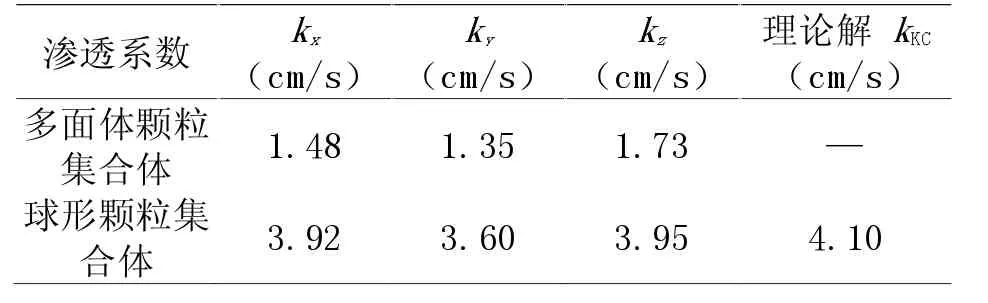
對影響土體滲透性的各因素的作用機理開展理論研究是當前研究的重要方面。李云川等[1]基于計算流體動力學與離散元耦合的數值模擬方法,研究了土壤滲透系數隨土層深度的變化規律。焦浩然等[2]從室內試驗和數值模擬兩個方面探討了細粒土在考慮應力作用下滲透特性研究進展。李華等[3]通過試驗發現黃土中孔徑為1.3μm 上述研究表明,土體的滲透受很多因素復雜影響,尋找定量的預測模型成為理論研究實用化的關鍵步驟。例如,包孟碟等[7]研究了級配與滲透系數的關系,建立了考慮級配曲線面積的滲透系數經驗公式;曹志翔等[8]根據水頭損失細觀機制推導了滲透系數理論計算公式,公式以孔隙率和等效粒徑為基本參數,具有明確的物理意義。Liu 和Jeng[9]以及劉一飛等[10]模擬了不同形態顆粒構成的土體的滲透系數,并修正了Kozeny-Carman 滲透系數公式;饒云康等[11]基于近百組粗粒土的滲透系數試驗數據,以全級配和土樣孔隙比作為神經網絡的輸入變量,利用遺傳算法訓練得到了粗粒土滲透系數預測模型。 上述擬合公式考慮的因素各有差異,預測結果精度各有不同,這是由于各個影響因素往往具有耦合影響。整體而言,目前對土體滲透性與顆粒形狀關系的系統研究還較少,綜合考慮各因素相互耦合的作用成果也較少。為此,本文采用數值模擬方法,探討顆粒形狀以及密實程度對粗粒土滲透特性的影響規律,以促進對土體滲透性的理論認識深度。 首先建立孔隙比為0.69 的球形顆粒和多面體顆粒集合體(相當于數值土體試樣),如圖1 所示。其中,孔隙比的計算公式為 式中,V 為顆粒集合體的總體積,Vs為所有顆粒體積之和。 圖1 數值土體試樣 顆粒集合體試樣中,球形顆粒粒徑在1.8mm到2.2mm 范圍均勻分布。多面體顆粒形狀共有6種,如圖2 所示,這些顆粒的最長軸與最短軸之比在1 到1.4 之間。多面體顆粒的等效粒徑為 式中,Vp為多面體顆粒的體積。 為與球形顆粒對比,多面體顆粒集合體中的顆粒等效粒徑也在1.8mm 到2.2mm 范圍均勻分布,6 種形狀顆粒的數量相同。 圖2 多面體顆粒的形狀 圖1 中同時給出了試樣在三個正交方向的切面。可以看到,在每個切面上固體部分(顆粒切面)排列非常不規律,使得流體在流經這些切面時受到不同程度的阻礙。此外,同一個試樣三個切面上的顆粒排列不盡相同。 采用Avizo 軟件的滲透特性模擬(Absolute Permeability Experiment Simulation)功能測試兩個試樣的沿三個正交方向的滲透系數。模擬方法為在兩相對面上分別施加不同的孔隙水壓力,兩相對面上孔隙水壓相差30kPa,其余四個面為不透水邊界。通過模擬一定時間內由高水壓面向低水壓面流動的水流量,即可由下式估算滲透系數: 式中,Q 為體積流速,?w為水的重度(10kN/m3),L 為流動距離,S 為垂直流向的橫截面積, ?p為壓力差(本文中為30kPa)。 孔隙穩態流場通過有限體積法求解簡化的NS 方程得到,假定流體不可壓縮,且為牛頓流體,處于層流狀態,流體和固體界面不可滑動。 圖3 為穩定流動時,孔隙內流體壓力的空間分布。整體上,孔隙流體壓力沿流動方向降低,在同一垂直流動方向的界面上,孔隙壓力分布并不均勻;孔隙連通性較好、顆粒稀疏的局部區域,流動阻力較小,孔隙壓力較低,是流體滲透的優勢通道。而對于孔隙連通性較差、顆粒密集的區域,流動阻力則較大,孔隙壓力較大。盡管多面體顆粒的等效粒徑與球形顆粒一致,但從圖1 及圖3 可以看到,多面體顆粒試樣中的孔隙被顆粒分割得更加零碎,流通孔道尺寸明顯小于球形顆粒試樣,定性上預示著流體更難通過多面體顆粒試樣,即它的滲透系數更小。 圖3 孔隙流體壓力分布 數值模擬得到的三個方向滲透系數結果如表1 所示。Kozeny-Carman 公式可用于估算球形顆粒集合體的滲透系數: 式中,? 為動力粘滯系數(0.001Pa·s),d 為平均粒徑(本文取2mm),n 為孔隙率,可由孔隙比算得: 表1 數值模擬結果與理論解 表1 中數值模擬的滲透系數在礫石、粗砂的常見滲透系數范圍內,說明了數值模擬的可靠性。從表1 可以看出,球形顆粒集合體三個正交方向的滲透系數相差不大,且與理論解結果基本吻合。而多面體顆粒集合體三個正交方向的滲透系數相差較大,這主要是由于多面體顆粒的排列整體上具有一定各向異性,特別是長、短軸差別較大的顆粒,其取向對滲透系數影響較為明顯。此外,多面體顆粒集合體的滲透系數僅為球形顆粒集合體滲透系數的40%;這是由于多面體顆粒試樣中的孔隙被顆粒分割得更加零碎,流體在孔隙中流動受到的阻力因而更大,滲透性因而降低。 圖4 進一步給出了本研究模擬的不同孔隙比試樣三向滲透系數平均值隨孔隙比的變化。如圖所示,滲透系數隨孔隙比增加而非線性增長,增加速率也隨孔隙比增大而增大。球形顆粒集合體的滲透系數始終小于理論解,但二者差別逐漸減小。多面體顆粒集合體的滲透系數受孔隙形狀的影響非常明顯,即使孔隙比達到0.85,其滲透系數也明顯小于球形顆粒集合體,兩者比值在35%到50%之間。 圖4 滲透系數隨孔隙比的變化 本文采用數值模擬方法研究了不同顆粒形狀的粗粒土滲透特性,獲得了滲透系數數值解。結合本文模擬結果和滲透系數理論公式可知,粗粒土的滲透系數與流體粘滯性、土體密實程度(孔隙比)、顆粒粒徑、顆粒形狀有關。本文模擬的球形顆粒和多面體顆粒分別代表了磨圓度很好的粗粒土和磨圓度很差(棱角分明)的粗粒土兩種特殊情況。結果表明,顆粒形狀越復雜,孔隙形狀的復雜程度越高,流體滲透越困難,滲透系數因而越低。多面體顆粒集合體的滲透系數明顯小于球形顆粒集合體,兩者比值在35%到50%之間。2 數值模型與模擬方法





3 模擬結果與討論

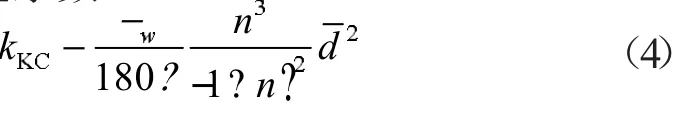


4 結論

