自然和諧授知識 水到渠成育素養
——“基本不等式的教學設計與反思

龐 燕

(江蘇省常州市田家炳高級中學 213000)

一、 基本情況

1.教材分析

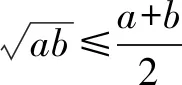
2.學情分析

學生有了不等式的基本知識作為鋪墊，對不等式的學習已具備基本的認識，而基本不等式來自生活，是從生活中抽象而來的，只要我們選材得當，能夠激發學生的學習興趣，學生也能夠較容易理解基本不等式的推導，且達到滲透數學思想、關注數學文化的目的．

3.目標設計

(1)學會推導并掌握基本不等式，理解基本不等式的幾何意義，并掌握定理中的不等號“≥”取等號的條件.

(2)探索并了解基本不等式的證明過程，在基本不等式的證明過程體會從特殊到一般的思維過程，領悟數形結合思想的應用．

(3)培養學生生活問題數學化，并注重運用數學解決生活中實際問題的意識.

4.教學重難點

本節課教學重點是應用數形結合的數學思想理解基本不等式，并從不同角度探索不等式的證明過程．

教學難點是基本不等式等號成立條件．

5.教學策略

本課在設計上采用了由特殊到一般、從具體到抽象的教學策略．利用數形結合、類比歸納的思想，層層深入，通過學生自主探究，分析、整理出推導公式的不同思路．同時，借助多媒體幾何畫板、視頻的直觀演示，幫助學生理解，并通過教師的點撥引導，師生互動、講練結合，從而突出重點、突破難點．

教法:問題引導、啟發探究和歸納總結相結合

學法:自主學習與合作討論相結合

教學手段:黑板板書為主結合多媒體輔助教學

二、 教學過程

1.創設情境，引入課題

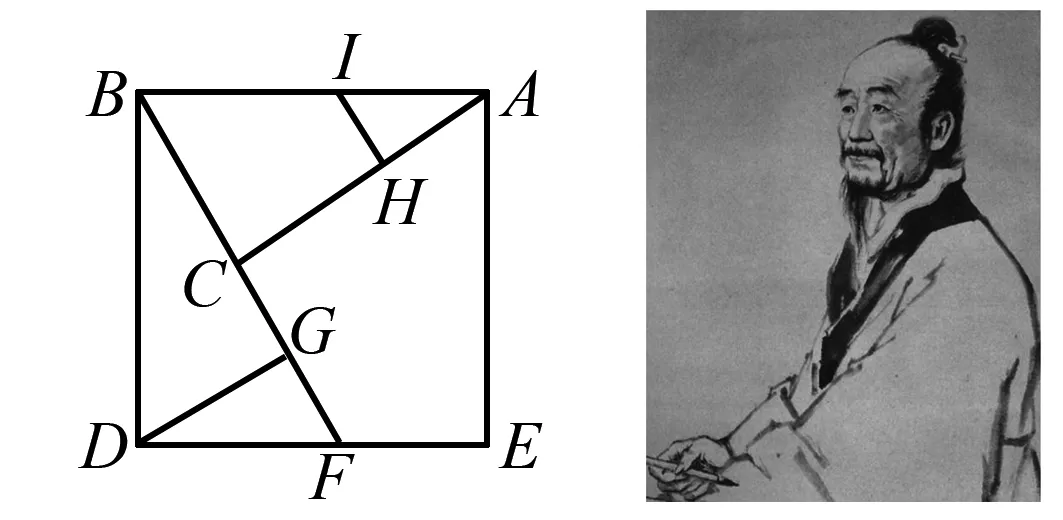
圖1 圖2

情境1 (展示并介紹古代弦圖)同學們現在看到的是中國古代數學中著名的一副圖，叫做弦圖．它是由我國三國時期的數學家趙爽設計的．早在1300多年以前，這位數學家就巧妙的利用弦圖中的面積關系證明了勾股定理，這是世界上最早證明勾股定理的方法之一．弦圖不僅造型美觀，而且蘊藏著很多玄機．

情境2 (展示24屆國際數學家大會會標)大家現在看到的是2002年在我們北京召開的第24屆國際數學家大會的會標．這個會標設計源于古代弦圖．它的色調明暗相間，使它看上去象一個風車，這不但象征中國人民的熱情好客，同時也充分展現了中國古代數學對世界所做出的重大貢獻．今天咱們也來研究一下弦圖．

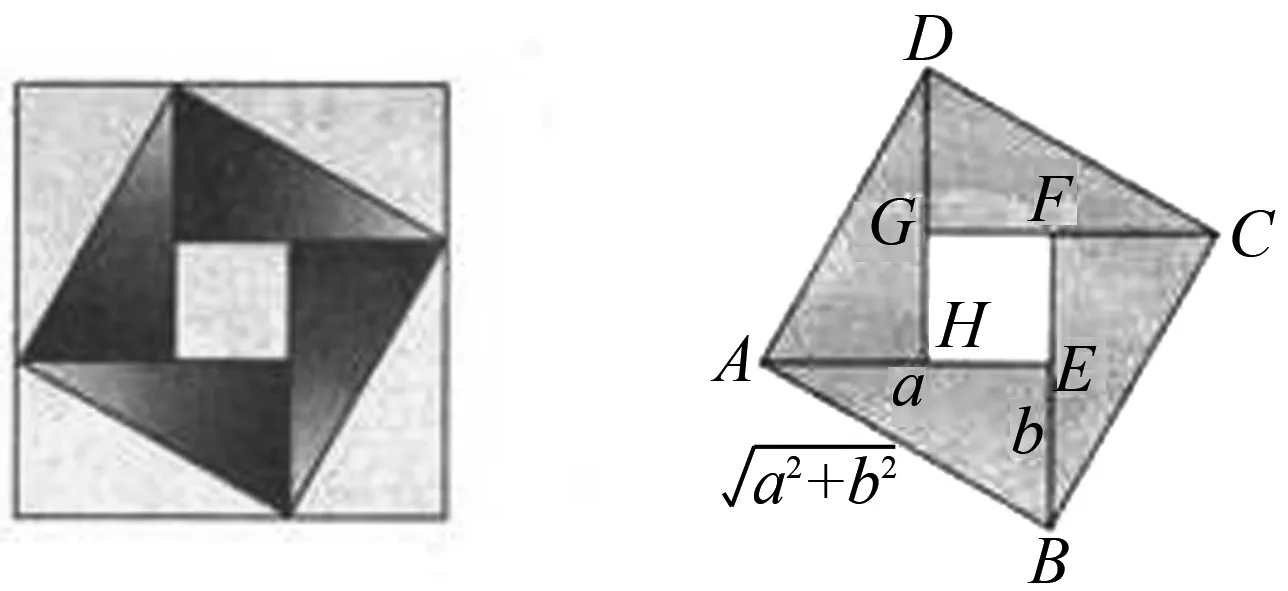
圖3 圖4

教師引導學生從面積的關系去找相等關系或不等關系．

(1)探究圖形中的不等關系

問題1 請觀察會標圖形，圖中有哪些特殊的幾何圖形?它們在面積上有哪些相等關系和不等關系?

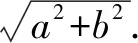
問題2 大家看，這個圖形里還真有點奧妙．我們從圖中找到了一個不等式．這里a、b的取值有沒有什么限制條件? 不等式中的等號什么時候成立呢？

當直角三角形變為等腰直角三角形，即a=b時，正方形EFGH縮為一個點，這時有a2+b2=2ab．

(2)得到結論：一般的，如果a,b∈R,那么a2+b2≥2ab(當且僅當a=b時取“=”號)

(3)思考證明：你能給出它的證明嗎？

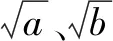
設計意圖通過問題情境的設計激發學生學習的積極性，培養學生的探究能力；其次，簡略介紹中國古代數學家趙爽的生平，滲透數學思想、關注數學文化．

2.深入探究，理解概念

填寫下表，教師結合幾何畫板計算并展示下面過程；

ababa+b2ab與a+b2的大小關系 121841622……

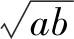
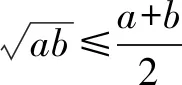
問題4 你能給出它的證明嗎？

證法1 用比較法證明.

證法2 用分析法證明.

設計意圖:通過引導，讓學生去證明猜想的結果，進一步鞏固比較兩個代數式大小的方法，并讓學生明白歸納、猜想、證明是我們發現世界、認知世界的重要的思維方法．

3.自主探究，深化認識

問題3能否給基本不等式一個幾何解釋呢？

探究：課本第98頁的“思考”

圖5

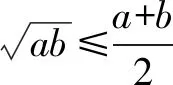
設計意圖:通過展示均值不等式的幾何直觀解釋，培養學生數形結合的意識，并使抽象的問題更加直觀、形象，使學生進一步加深對均值不等式的理解．

4.實際運用，強化新知

例題(1)用籬笆圍一個面積為100m2的矩形菜園，問這個矩形的長、寬各為多少時，所用的籬笆最短，最短的籬笆是多少？(2)一段長為36m的籬笆圍成一個矩形菜園，問這個矩形的長、寬各為多少時，菜園的面積最大．最大面積是多少？

設計意圖:讓學生初步運用基本不等式解決實際問題, 通過對實際問題的解決讓學生體會數學來源于生活，同時又服務于生活．

三、教學反思

1.融入數學史，讓學生親歷感受新知的建構過程和應用價值，體會數學的自然、合理，有價值

2.讓核心素養融入數學的概念教學，培養學生思維的創造性和嚴謹性

3.以學生已有的經驗為基礎設計問題，充分調動每一位學生的積極性