基于神經網絡的電子戰人力資源規劃分析

劉歌聲，趙祿達，沈從勇

(國防科技大學，安徽 合肥 230037)

0 引 言

電子戰越來越成為現代局部戰爭中的決定性、制勝性力量，在近期的美伊、美俄中東局部沖突中都發揮出左右戰爭結果的巨大作用。而電子戰在實際作戰過程中需要大量電子戰人員的參與，包括電子戰軍官、士官、技師以及文職人員等。

隨著現代智能化戰爭的迅速發展，第4代、第5代電子戰裝備陸續問世，各國電子戰能力的大幅提高，電子戰人員的需求量也出現了大幅的增長。這樣，電子戰人力資源規劃問題就顯得格外重要。目前，國內外對電子戰的研究主要集中于政策、體制編制方面[1-2]，而對電子戰人力資源規劃的研究還不廣泛，按照現代戰爭的發展趨勢對電子戰人員需求變化趨勢進行研究還很少。

本文研究基于神經網絡理論的電子戰人力資源規劃方法，通過建立兵力需求規劃模型、神經網絡預測模型和電子戰k級人員補充模型，為電子戰人力資源規劃提供了一種有效的思路和方法。

1 電子戰人力資源規劃思路分析

軍事人員的人力資源規劃主要是軍事人員系統狀態分析。系統狀態隨時間的演變主要與內外的人員流動有關。系統內部流動有晉升、降級、平調等；內部與外部之間的流動有招募(入伍、調入、提干等)、退休、轉業、復原、調出和其他減員等[3]。

本文研究電子戰人員規劃的思路和方法主要是分為3個過程，即首先按照總體兵力，根據國內外形勢變化，確定電子戰兵力比例，得到電子戰兵力，其次通過若干間隔時間計算的電子戰兵力數據代入神經網絡模型，推測下一階段的電子戰兵力數量，最后通過推測的電子戰兵力數量對電子戰人員補充系統進行人員數量信息的確定。通過以上步驟，將電子戰人力資源規劃從頂層到底層進行連貫分析，可以為決策者提供很好的決策輔助。電子戰人力資源規劃過程如圖1所示。

2 電子戰人力資源規劃模型構建

2.1 電子戰兵力需求規劃模型

一般而言，兵力規劃對于某個國家的軍隊來說屬于戰略層級的任務。但電子戰兵力的規劃有靈活、多變的特點，隨著戰場和階段任務的實時變化會產生很多無法預測的情況，所以電子戰兵力規劃一般需要結合戰略、戰役層級以及國家發展需求等實際情況共同考慮[4]。

首先，基于國家軍事戰略、國內外政治、經濟、外交等情況和重大突發性事件影響(戰爭突然爆發、發生大型自然災害以及重大衛生防疫事件等)因素，保證部隊正常運轉的條件下，兵力規劃目標為打贏隨時可能發生的局部沖突和戰爭。其次，綜合考慮以上因素后，根據可能對手的電子戰兵力數量，依據專家經驗以及敵我兵力數量、狀態比等因素，確定電子戰兵力需求比n。最后，再根據國家部隊總員額得出各個時期電子戰兵力的數量。那么，在模型1中總共需要確定以上4個具體數值ni(i=1,2,3,4)。

2.2 神經網絡預測模型

神經網絡理論是根據現代人類神經系統的研究慢慢發展而來的，是一種通過模擬人類神經活動和神經信息傳遞方式對數據信息進行處理、練習，產生一定的處理信息規律，對未知信息進行進一步處理、預測和分類。經過50多年的發展，神經網絡理論被各行各業認同和廣泛運用，可分為前饋網絡(多層感知機)和反饋網絡(Hopfield網絡)。其中，比較著名的是BP神經網絡(NN)、RBFNN、GRNN、PNN、支持向量機等。本文主要以BP神經網絡和RBF神經網絡2種算法對電子戰人員進行數據處理和預測。

2.2.1 BP神經網絡預測模型

BP人工神經網絡模型一般有3個基本要素：輸入層(Input)、隱含層(Hidden)以及輸出層(Output)。數據需要在網絡中進行不斷的迭代和訓練，從而找到一套合適的連接權值，對數據可以進行預測和分類。

BP神經網絡作為反饋型神經網絡的代表，具有很好的系統魯棒性。網絡連接示意圖如圖2所示。

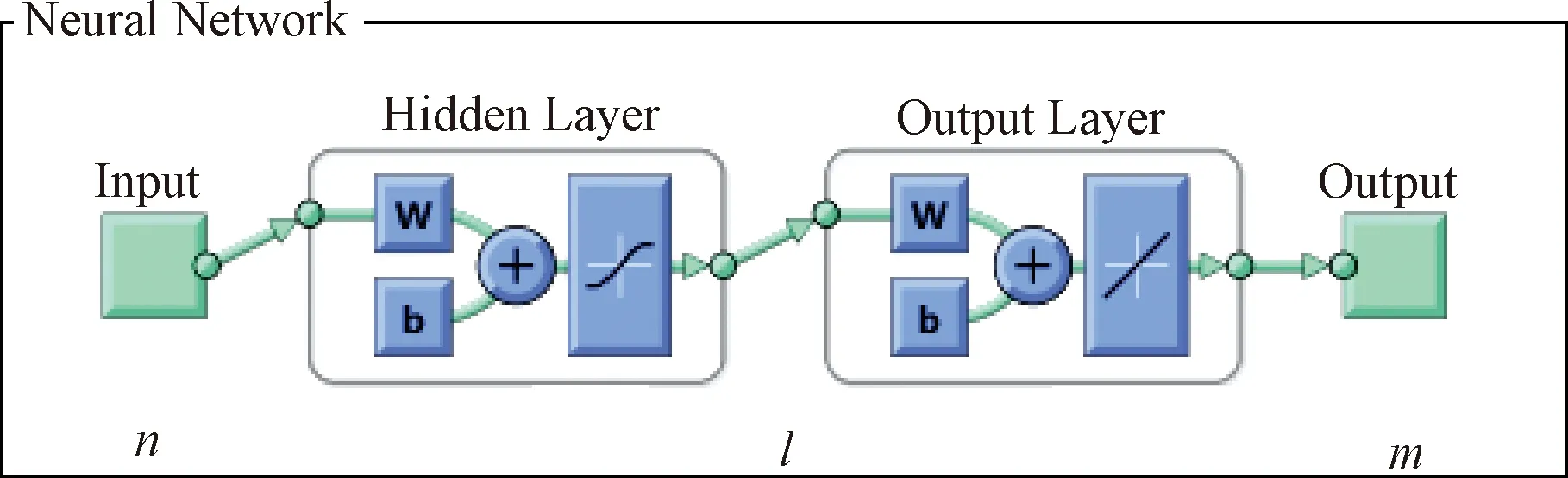
圖2 BP神經網絡連接示意圖

其具體步驟如下：

Step1：網絡初始化。確定必要的網絡參數，一般有輸入層節點數、隱含層節點數、輸出層節點數、連接權值和閾值、傳遞函數種類等;

Step2：根據步驟1確定的各項參數，進行隱含層輸出計算;

Step3：同上，進行輸出層輸入計算;

Step4：計算網絡誤差=期望輸出-網絡預測輸出;

Step5：根據網絡誤差和網絡學習速率，更新連接權值和閾值;

Step6：判斷算法是否結束，若未結束，返回步驟2繼續進行網絡訓練。

需要說明，一是傳遞函數有很多種，一般選用閾值型傳遞函數(hardlim)；二是網絡數據在訓練過程中需要的是歸一化后的數據，這就要求在數據輸入前進行(0，1)的數據歸一化，在數據輸出時再進行數據還原；三是一般來說，隱含層節點數需要人為確定，設輸入層節點數為n，隱含層節點數為l，輸出層節點數為m，滿足以下關系：

(1)

2.2.2 RBF神經網絡預測模型

進一步，由于BP神經網絡在連接權值上一般需要反復迭代進行確定，對于大量數據處理過程會產生比較大的時延。而RBF徑向基神經網絡通過求輸入樣本和隱藏層點(中心點)的范數，將其代入徑向基函數(高斯函數，二次函數，逆二次函數等)得到一個數值，再與之后的權值相乘加和，就得到了相應的輸出，其網絡簡單，學習收斂速度很快。其總體的表達為：

(2)

式中：ω為連接權值，可通過最小二乘法迭代得到，計算式為：

i=1,2,…,h;p=1,2,…,P

(3)

具體的學習算法步驟如下：

Step1：使用K均值聚類方法求解徑向基函數中心，一般經過網絡初始化、將輸入數據按照最近鄰規則分組、重新調整聚類中心3步完成；

Step2：求解RBP神經網絡徑向基函數方差；

Step3：使用最小二乘法計算隱含層和輸出層間的權值。

M國、E國和Z國從2009年至2019年電子戰人員變化曲線如圖3所示。可見，電子戰人員的需求量隨著現代戰爭發展以及國際形勢變化會呈現出非單調的擺動發展序列或者具有飽和狀態的S形序列，使用神經網絡對其進行數據預測比較恰當。

圖3 M、E、Z國2009～2019年電子戰人員變化趨勢圖

2.3 k級人員補充模型

對于電子戰人員系統，一定是不斷有人從中離開，因而要保持各類人員的數量必須進行人員補充(如招收新的人員以及人員的晉升等)。k級人員補充模型就是根據當前的人員分布、將來希望的人員分布以及離開人員的數量(比例)，計算晉升和招收的各類人員的數量。

用ni(t)表示在時刻t，i級的人員數；nj(0)表示在當前時刻j級的人員數；mij(t)表示在區間(t-1,t]內從i級轉移到j級的人員數；ri(t)表示在區間(t-1,t]內從外部招收到i級中的人員數；mi0(t)表示在區間(t-1,t]內從i級離開系統的人員數(i=1,2,…,k；j=1,2,…,k；t=1,2,…)。

在此考慮具有k級的嚴格等級人員系統。由人員流動的平衡關系，由k-1級向k級晉升滿足：

mk-1,k(t)=nk(t)-nk-1(t)+mk0(t)

(4)

在每級之間的mij(t)由各級間的晉升比例確定(編制、戰斗力需求等因素影響)，則mk-1,k(t)與mk-2,k-1(t)均為已知量，可以得出遞推關系：

(5)

可以發現，在調整i-1級人員比例時出現本級人員積壓過多的現象，導致該級流出(包括離開機構以及向上級晉升)人員小于希望本級減少的人員數量，向i級的晉升m(i-1)i(t)會產生負值，顯然不符合實際，對式(5)做出如下改進：

(6)

同樣地，如果i-1級人員數量過小，需要晉升的人員數比原有數量還要多時，對式(6)做出如下改進：

(7)

這樣，通過模型1將各個階段電子戰兵力大致數量確定，代入模型2中，將未來需要了解階段內的電子戰兵力人數進行預測，在模型3 中對電子戰人員系統進行人員增減的具體討論，就可以對電子戰人力資源規劃提供一個清晰的思路流程。

3 電子戰人員補充算例預測與分析

以Z國電子戰人員數據為例，進行電子戰人員補充算例預測與分析。下面按照電子戰人力資源規劃流程，將原始數據(2009～2019)分為兩部分，前10年數據為基礎數據，第11年數據為驗證數據，進行3個模型的求解，進而預測后一階段的電子戰人員數量，求解人員補充模型具體解。

3.1 Z國電子戰兵力整體需求

在第1個模型中，首先將原始數據(2009～2018年Z國軍事人員數量)進行初始化，按照軍事戰略發展和世界軍事發展趨勢等因素確定電子戰兵力各階段初始化數據，并且電子戰兵力序列為(12.6,15.4,17.44,23.76,28.1,31.1,34.42,28.14,33.35,44.35,35.8)。如表1所示。

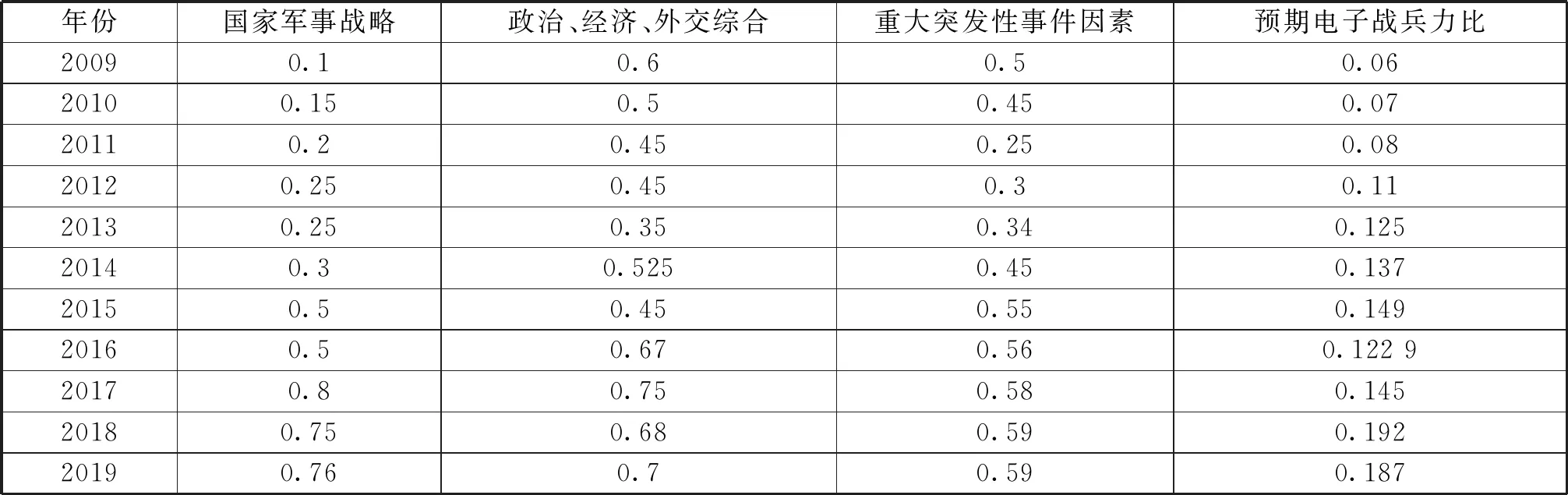
表1 Z國電子戰兵力各階段初始化數據

3.2 Z國電子戰兵力神經網絡模型預測

3.2.1 BP神經網絡預測[5-6]

按照BP神經網絡建立步驟，首先建立4-9-1結構的BP神經網絡，如圖4所示。

在結果的討論中，我們加入決定性系數來討論相對誤差的大小。

設相對誤差：

(8)

圖4 Z國電子戰BPNN模型結構

式中：Tsim為兵力預測結果；Ttest為兵力實測結果。

決定性系數為：

(9)

3.2.2 RBF神經網絡預測

按照RBF神經網絡的建立步驟，同BP神經網絡數據處理相類似建立模型。

節點的徑向函數φ為高斯函數：

(10)

式中：‖·‖取歐式范數;c為函數中心;σ為函數方差，求解方法為：

(11)

通過以上方法，代入模型1求的相關數據，得到表2結果。

表2 Z國電子戰人員神經網絡預測數據

在BP神經網絡預測的訓練測試誤差和總體誤差(9組數據)進行誤差分析，其決定性系數擬合值變化圖像如圖5所示，圖中橫縱坐標分別表示輸入樣本數據和預測數據的誤差值，若以Y代表預測誤差，兩者的誤差擬合方程分別為：

Y1=0.92·A+0.041

(12)

Y2=0.83·A+0.12

(13)

式中：A為當前樣本在總樣本中所占比例。

圖5 誤差決定性系數變化

可見，2種神經網絡在具體算例計算過程中相對誤差比較相近，但對于遇到大數據樣本時，BP神經網絡由于反饋迭代連接權值過程比較耗時，此時RBF神經網絡就會更節約時間。

3.3 Z國電子戰兵力k級人員補充需求

按照模型2預測出Z國2020年度電子戰兵力數量取45.065 0萬人，代入模型3中進一步求解人員補充需求。

假設Z國電子戰兵力系統有4級，各級之間人員需保持3∶1的數量關系，則可得出各級人員序列為nj(t)=(30.417 4,10.139,3.380,1.127)，模型3滿足：

(14)

解得:m10(t)=47.36,m20(t)=21.43,m30(t)=8.91，m40(t)=3.86，r1(t)=74.86。

這樣，就得出了Z國在2020年電子戰兵力的預期需求，獲得了實際電子戰兵力結構中各級的晉升、退役大致人數，可以為兵力整體規劃提供很好的決策依據。

3.4 幾點說明

通過以上算例，說明整個電子戰人力規劃十分有效，可以為指揮員提供很好的決策依據。但還存在幾點不足：一是整體規劃流程在模型1中考慮了突發事件的影響，在另外2個模型中考慮的還不夠細致；二是k級人員補充模型中表示的嚴格等級系統只允許第1級直接從外部招收人員。而實際上等級系統也需要在其他級直接招收新的人員(比如對特殊電子戰人才的招收和戰時的緊急動員)，這樣進入某級的人員就會分為下級晉升和外部招收兩部分，等級就會拓展為非嚴格的等級系統，可運用各級之間的人員轉移矩陣進行關系表示，運用馬爾科夫轉移網絡也可以得出相應結論，有待進一步討論。

4 結束語

在未來智能化聯合作戰中，電子戰必定是左右戰爭勝負的關鍵一環，而電子戰人力資源規劃就顯得尤為重要了。而目前對于這方面的研究很少，基本停留在定性分析上。本文立足于以往人員數據和經驗結論，運用2種神經網絡進行模型分析和數據預測，為電子戰人力資源規劃提供了一個切實可行的定量分析方法。經實際數據演算，該方法的確能夠對電子戰人力資源規劃起到輔助決策的作用。