基于卡爾曼濾波的IFM系統測量LFM信號載頻方法

張 雷，李廣強

(1.解放軍95865部隊，北京 102218； 2.空軍預警學院，湖北 武漢 430019)

0 引 言

比相法瞬時測頻接收機，簡稱瞬時測頻(IFM)接收機，是一種通過頻率-相位變換實現頻率測量的間接測頻系統，不僅具有體積小、頻帶寬、截獲概率高的特點，而且較好地解決了截獲概率和頻率分辨力之間的矛盾，是機載雷達告警器和雷達對抗偵察設備中經常采用的技術。線性調頻(LFM)信號是現代雷達廣泛采用的一種脈沖壓縮信號，也是雷達對抗偵察重點分析的信號樣式之一。但是傳統的IFM系統在一個脈沖信號持續時間內，通常只在脈沖前沿進行一次頻率測量，因此無法準確獲取線性調頻信號及其脈內調制信息[1]，從而限制了IFM接收機的使用。

文獻[2]采用了模數轉換(ADC)和線性回歸的方法，估計出LFM信號的載頻和調頻系數，但是只能在全部采樣點的頻率估值完成后，才能估算調頻系數，實時性不夠好，因此需要研究更合適的方法。傳統IFM系統的微波鑒相器通常輸出I、Q兩路正交電壓，之后采用極性量化或AD量化的方法得到頻率數據。根據文獻[3]的分析，IFM系統具備測量LFM信號的潛力，本文在此基礎上展開研究，對I、Q信號進行AD量化后，通過卡爾曼濾波方法實現IFM系統對LFM信號頻率參數的估計。

1 IFM系統原理及測量LMF信號分析

1.1 傳統IFM系統基本原理

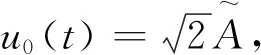
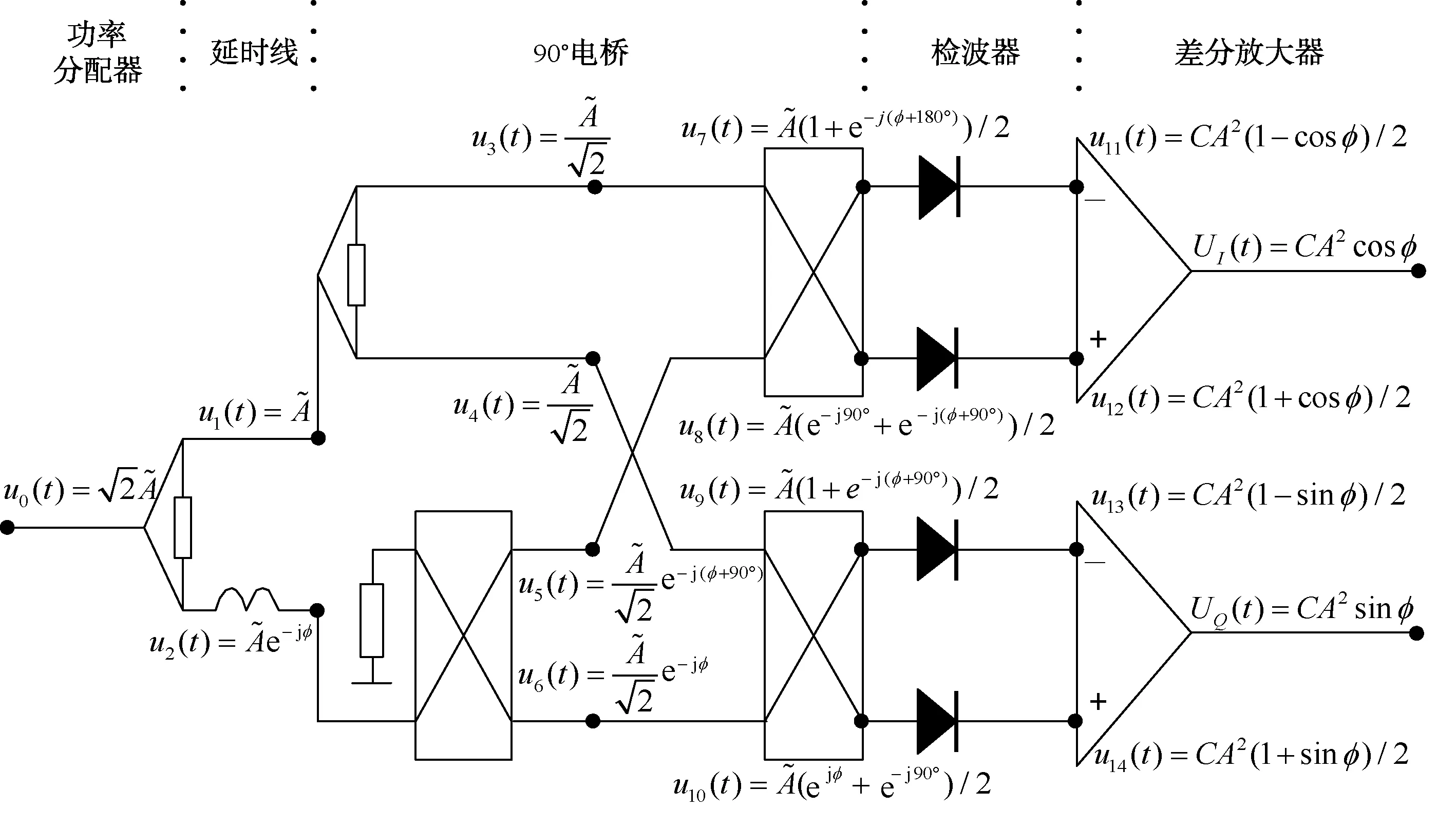
圖1 一種實用的微波鑒相器原理圖

為了解決測頻范圍和頻率分辨力的矛盾，實際中一般將多個鑒相器并行使用，短延遲線用于擴大測頻范圍，長延遲線用于提高頻率分辨力。圖2為k路鑒相器并行使用的IFM系統組成和原理圖，相鄰鑒相器延遲時間比為n，各鑒相器輸出的相位值為φi，i=1,2,3,…,k，最短延遲時間不存在測頻模糊，則逐級迭代解模糊和相位校正的計算公式如下[4]：

(1)

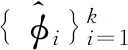
為提高測頻精度，之后一般用所有鑒相器的相位輸出對頻率進行最小二乘估計[4]：

(2)

式中:T為最短延遲線的延遲時間;n為相鄰2路鑒相器的延遲時間比;k為鑒相器路數；f0為無模糊測頻范圍內滿足f0T乘積為正整數的最小頻率值。

在實際工作中，通常k的取值為3或4，n的取值為4或8[4]。

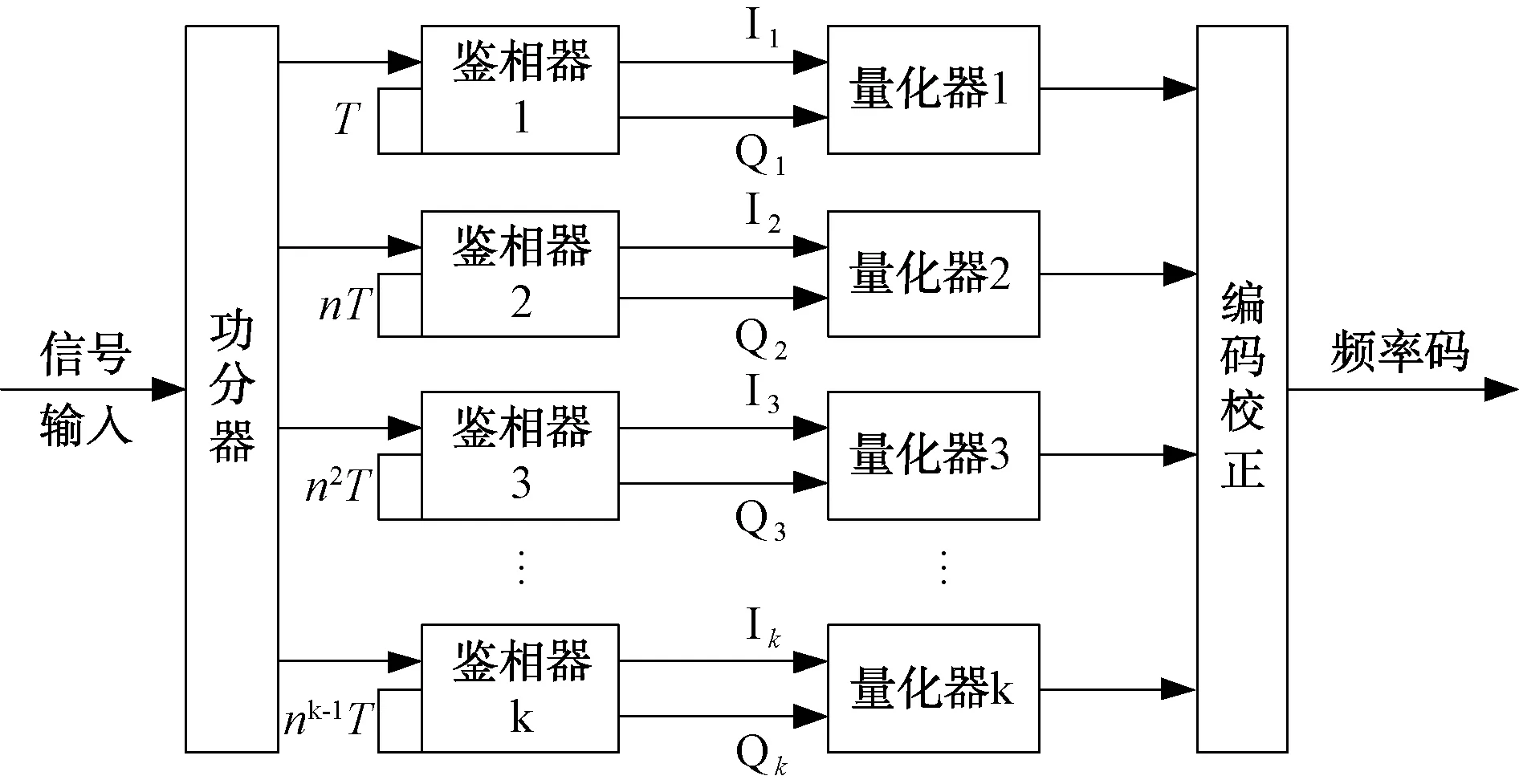
圖2 k路鑒相器并用IFM系統組成和原理圖

1.2 傳統IFM系統對LFM信號處理模型

首先從理論上分析IFM系統對LFM信號的響應情況，假設圖1中輸入信號u0(t)為一線性調頻信號，即:

(3)

式中:f0為信號載頻(即起始頻率);K為調頻系數。

則1～14節點的信號分別為[3]:

(4)

(5)

(6)

(7)

(8)

由于T為ns量級，K為幾十到幾百MHZ/μs，所以2πf0T?πKT2，因此式(8)可近似簡化為：

(9)

通過式(9)可得到相位差φ。多路鑒相器并用時，不同延遲時間的其他路相位差φi同理可得到，再根據式(2)可得到載頻的估計值，重復間隔、脈寬等參數值仍按照原方式測量。由此可見，IFM系統在理論上具備測量LFM信號頻率的能力，但需要對后續的信號處理方式進行改進。

2 改進IFM系統測量LMF信號方法

通過上一節分析可知，LFM信號進入傳統IFM系統，經過微波鑒相器也輸出I、Q兩路正交電壓，由于傳統IFM系統在脈沖持續時間內只進行一次時間采樣，所以只能得到一個載頻值。如果對鑒相器輸出的時間連續信號UI、UQ進行AD量化，根據式(2)得到載頻估計值序列，再將估計值進行卡爾曼濾波，經過遞推運算，在脈沖持續時間內能夠得到精度較高的載頻值和調頻系數，從而可以實現IFM系統對LFM信號的實時測量。

2.1 卡爾曼濾波模型

卡爾曼濾波是一種時域濾波方法，利用含有噪聲的觀測值對動態系統的當前狀態進行最優估計，采用了狀態空間的方法描述動態系統，算法則采用了遞推的形式，便于計算機編程實現，數據實時更新，對數據存儲量的要求低，既可以處理平穩隨機過程，也可以處理多維和非平穩過程，廣泛使用于導航、制導、全球定位、目標跟蹤等領域。

假如有一個線性的動態系統，該系統可以表示為Xt=AXt-1+BUt-1+W，即系統當前時刻的狀態可以根據上一時刻的狀態和控制變量來推測，其中Xt為系統在t時刻的狀態，A為狀態轉移矩陣，Ut-1為t-1時刻系統的控制量，B為控制矩陣，W為系統過程噪聲。如果可以使用某種傳感器觀測系統的狀態值Xt或與Xt相關的其他參數，則卡爾曼濾波器的計算過程如下[5]：

(1) 觀測方程

Zt=HXt+V

(10)

式中:Zt為系統在t時刻的觀測值;H為觀測矩陣;Vt為觀測噪聲。

(2) 狀態預測方程

(11)

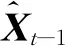
式(10)和(11)中X、U、W、Z、V均為多維向量，W和V一般假設為均值為0、協方差矩陣分別為Q和R的不相關高斯白噪聲，Z的維數等于或小于X。

(3) 協方差矩陣預測方程

Pt|t-1=APt-1AT+Q

(12)

式中:Pt-1為t-1時刻的協方差矩陣;Pt|t-1為根據t-1時刻的協方差矩陣Pt-1計算的t時刻的協方差矩陣預測值。

(4) 濾波增益矩陣方程

Kt=Pt|t-1HT[HPt|t-1HT+R]-1

(13)

式中：Kt為t時刻的濾波增益矩陣。

(5) 狀態更新方程

(14)

(6) 協方差矩陣更新方程

Pt=(I-KtH)Pt|t-1

(15)

式中：I為單位矩陣。

2.2 采用卡爾曼濾波的改進IFM系統

圖2中雖然含有非線性器件，但整體是一個對線性信號相關參數進行測量的系統，因此可以認為是一個線性系統，根據LFM信號載頻表達式f=f0+Kt推導系統的狀態方程，將式(9)作為觀測方程，從而采用卡爾曼濾波得到LFM信號的估計參數。

需要估計的LFM信號參數主要是載頻f和調頻系數K，則系統的狀態Xt為：

(16)

設Δt為時間間隔，根據LFM信號載頻表達式，有ft=ft-Δt+KΔt，調頻系數K為常量，且該系統中無控制量，所以狀態轉移矩陣為A=[1,Δt;0,1]，系統狀態方程為：

(17)

令Q為W的不相關協方差矩陣，由于式(17)描述的系統狀態是準確的，影響因素是雷達發射機性能，所以認為過程噪聲為0，即Q=[0,0;0,0]。IFM系統只能測量信號的頻率，所以觀測矩陣為H=[1,0]，觀測方程為：

(18)

IFM系統的測頻誤差為時間誤差與相位誤差之和，其中時間誤差是由延遲線的物理特性引起的，相位誤差包括鑒相器誤差、量化誤差、系統噪聲誤差以及式(9)的截斷誤差等。其中鑒相器誤差服從高斯分布，各誤差變量的影響因素不同，可以認為是相互獨立的，因此可假定IFM系統測頻誤差服從均值為0、方差為σ2的高斯白噪聲，則V的方差R=[σ2]。至此，卡爾曼濾波模型建立完成。

圖3為采用了多路ADC和卡爾曼濾波器的改進IFM系統，多路ADC的相位采樣輸出首先按照式(1)和式(2)解算載頻值，然后經卡爾曼濾波器輸出降噪后的載頻值和調頻系數，輸出顯示部分將載頻和調頻系數的數值以及載頻曲線直觀地顯示出來。卡爾曼濾波近似實時進行，可以認為延時為0；轉換時間短的ADC可達幾十ns量級，因此經過改進的IFM系統測量信號的延遲時間仍為ns級，不影響IFM系統對實時性的要求。

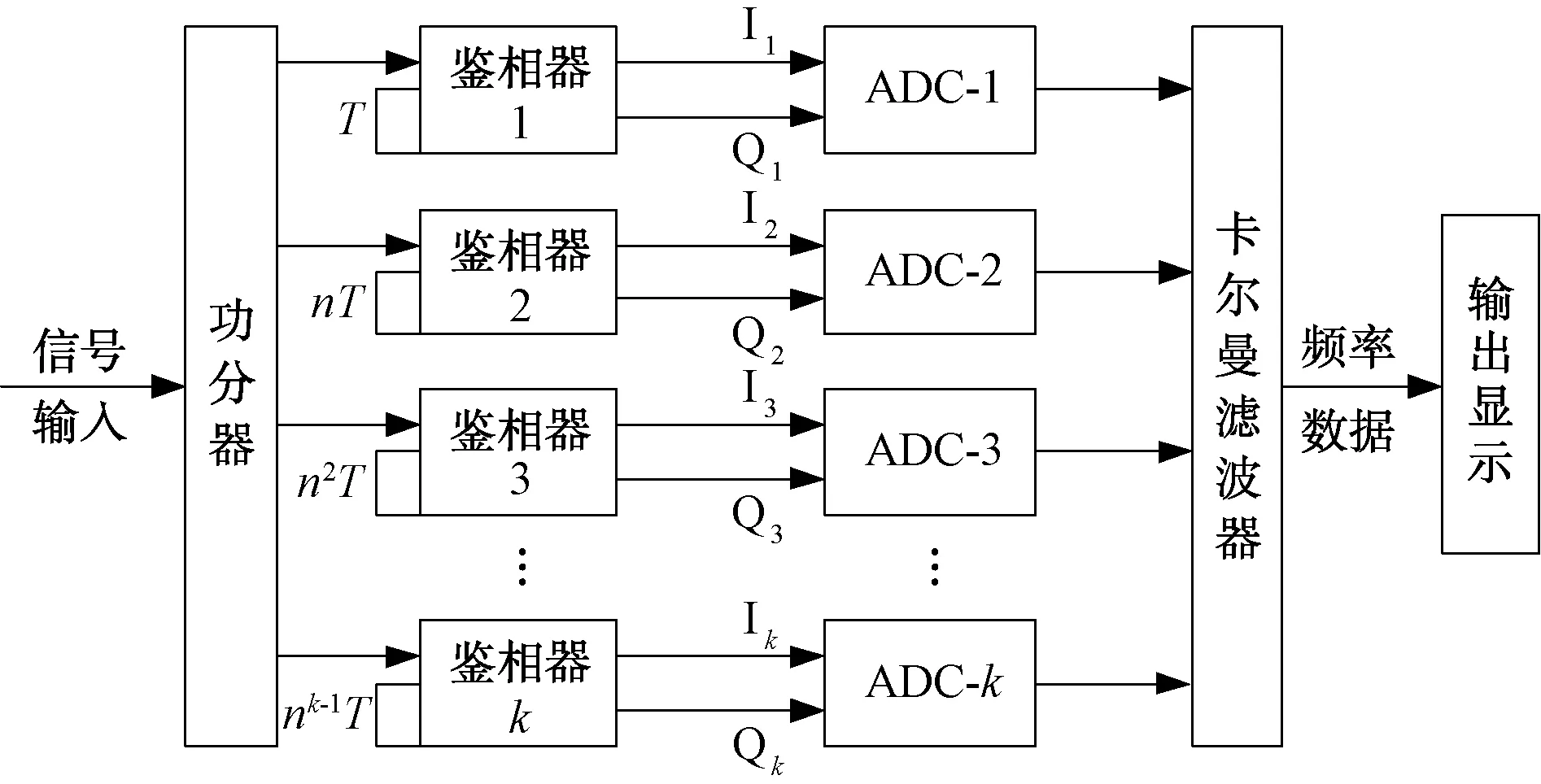
圖3 改進的k路鑒相器并用IFM系統

3 仿真及分析

為驗證改進IFM系統的有效性，采用文獻[2]中的線性調頻信號參數，使用MATLAB進行仿真。假設采用4路鑒相器并用的改進IFM系統，基本延遲線延遲時間為50 ns，延遲時間比為4，即k=4，T=50 ns，n=4；線性調頻信號的起始頻率為4 000 MHz，終止頻率為4 200 MHz，脈寬為10 μs，即f0=4 000 MHz，τPW=10 μs，K=20 MHz/μs；傳統IFM接收機測頻誤差為2 MHz，即σ=2 MHz；模擬采樣點數為1 000點。在卡爾曼濾波初始化時，將第1個觀測值設置為第1個卡爾曼估計值f1，初始調頻系數設置為1 MHz/μs，初始協方差矩陣設置為[σ2,0;0,1]，從第2個采樣點開始進行迭代運算。

3.1 采用卡爾曼濾波的改進IFM系統輸出

采用以上數據進行仿真，得到采樣后未經卡爾曼濾波和經過卡爾曼濾波的LFM信號時間-載頻圖，如圖4和圖5所示。在圖4中，雖然可以觀察出信號的載頻值近似呈線性變化，但存在較大的誤差噪聲，而且無法直接得到調制系數的準確估計值；在圖5中，載頻的誤差噪聲明顯減小，測得終止頻率為4 199.7 MHz；每一個采樣點的載頻和調頻系數估計值都可實時給出，在第800到1 000個采樣點處(即8～10 μs)，調頻系數約為19.98 MHz/μs，較文獻[2]中測得的調頻系數19.87 MHz/μs，精度進一步提高；根據終止頻率和調頻系數，計算得到初始頻率f0為3 999.9 MHz。

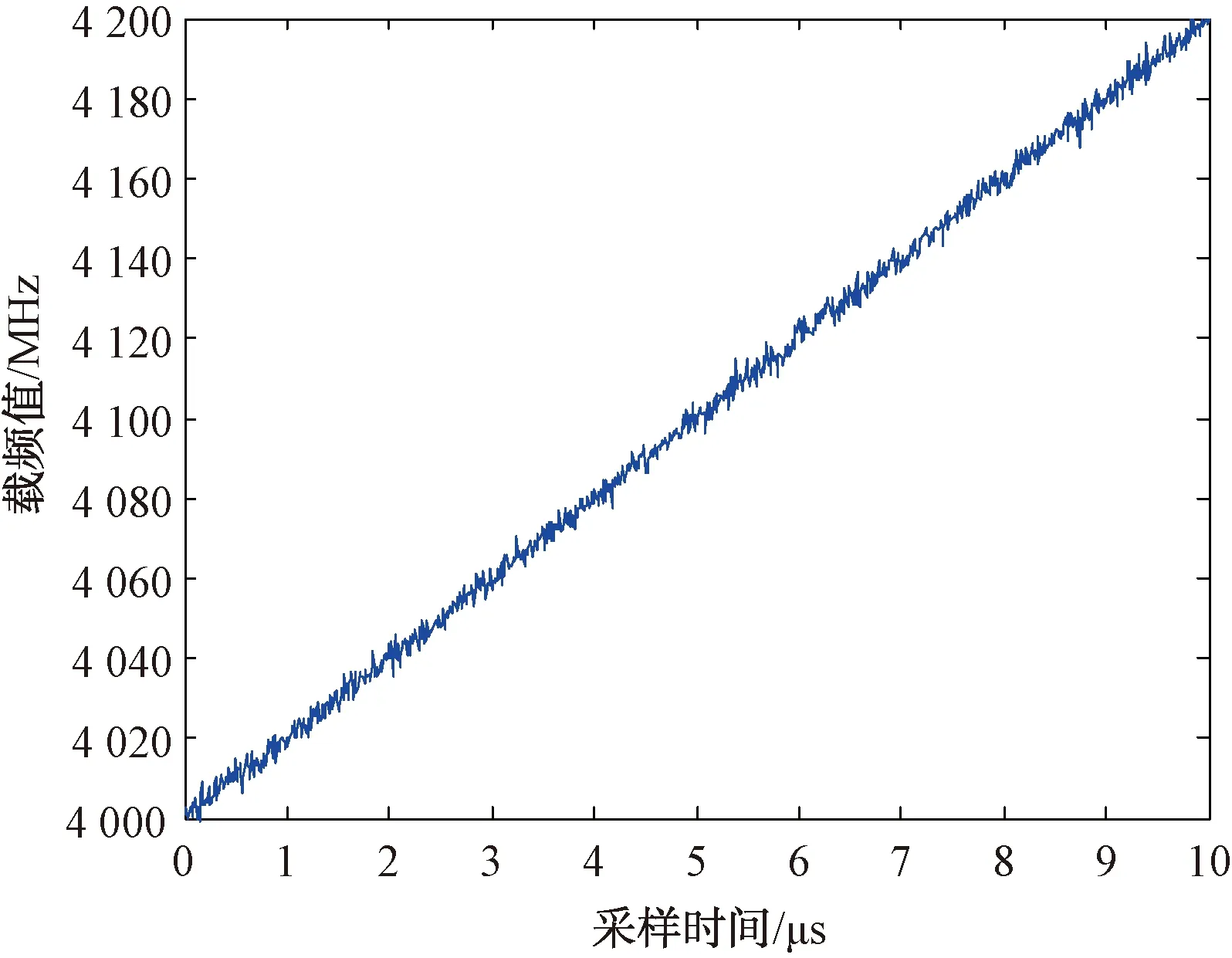
圖4 未經卡爾曼濾波的LFM信號時間-載頻圖

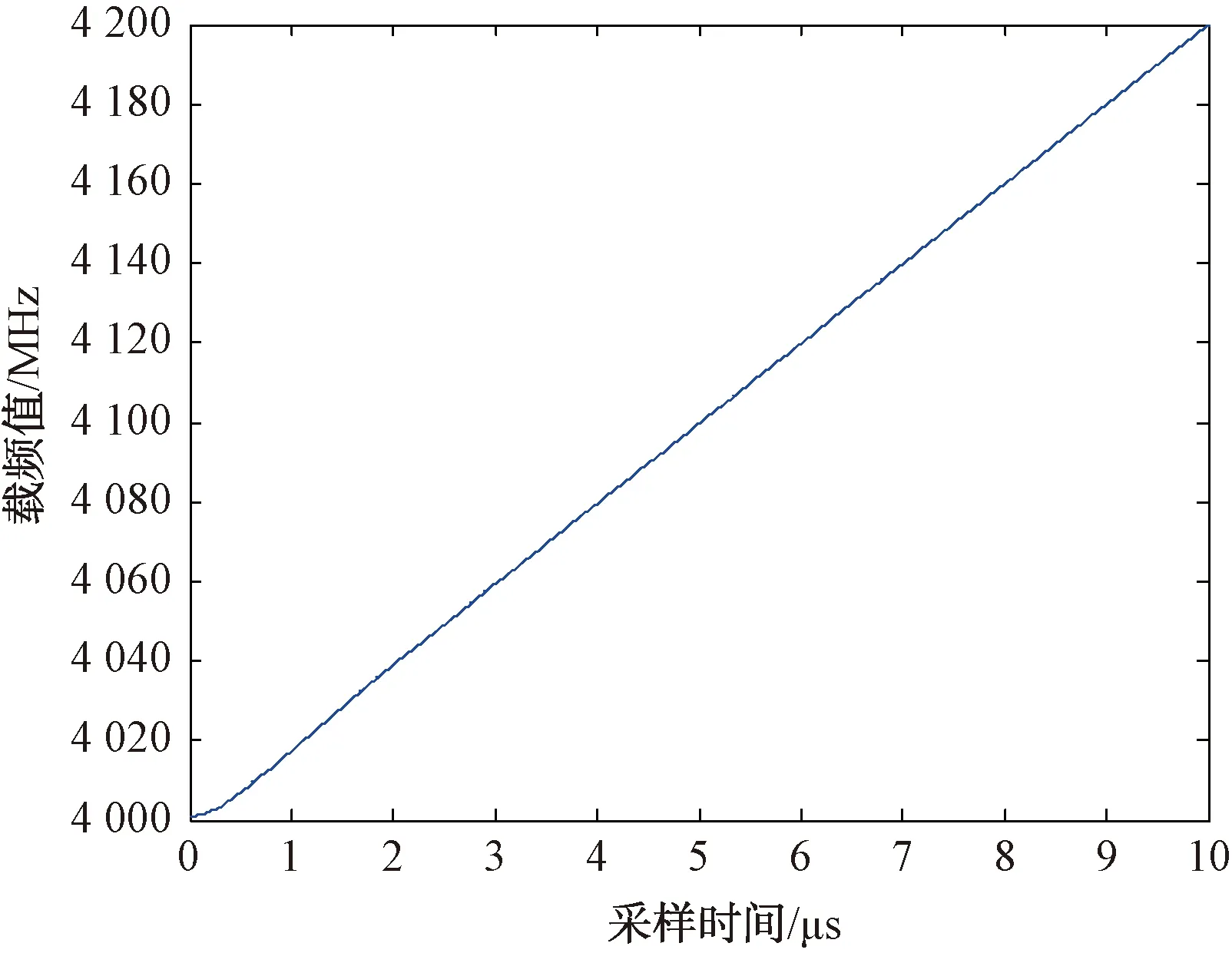
圖5 經過卡爾曼濾波的LFM信號時間-載頻圖

3.2 誤差分析

圖6和圖7分別為卡爾曼濾波后的LFM信號的載頻誤差曲線和調頻系數誤差曲線，從圖中可以看出，在脈沖持續時間末段，載頻誤差和調頻系數誤差都近似為0，但測頻誤差經過約2.2 μs的震蕩后才趨于穩定，最大誤差達到了4.1 MHz。但是該震蕩誤差并不會影響對信號的實時判讀，而且可以在事后分析信號時，使用終止頻率和調頻系數反推前段的載頻數據，從而消除震蕩誤差的影響，獲取整段脈沖的載頻精確值。總體來看，經過卡爾曼濾波，IFM系統的測量精度明顯提高。

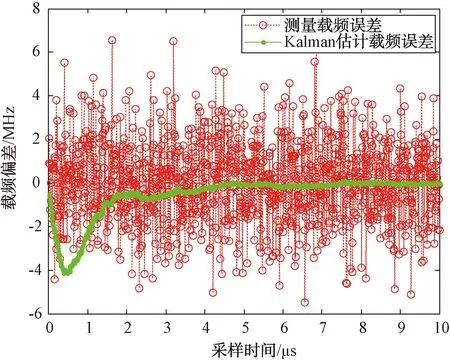
圖6 經過卡爾曼濾波的LFM信號載頻誤差曲線

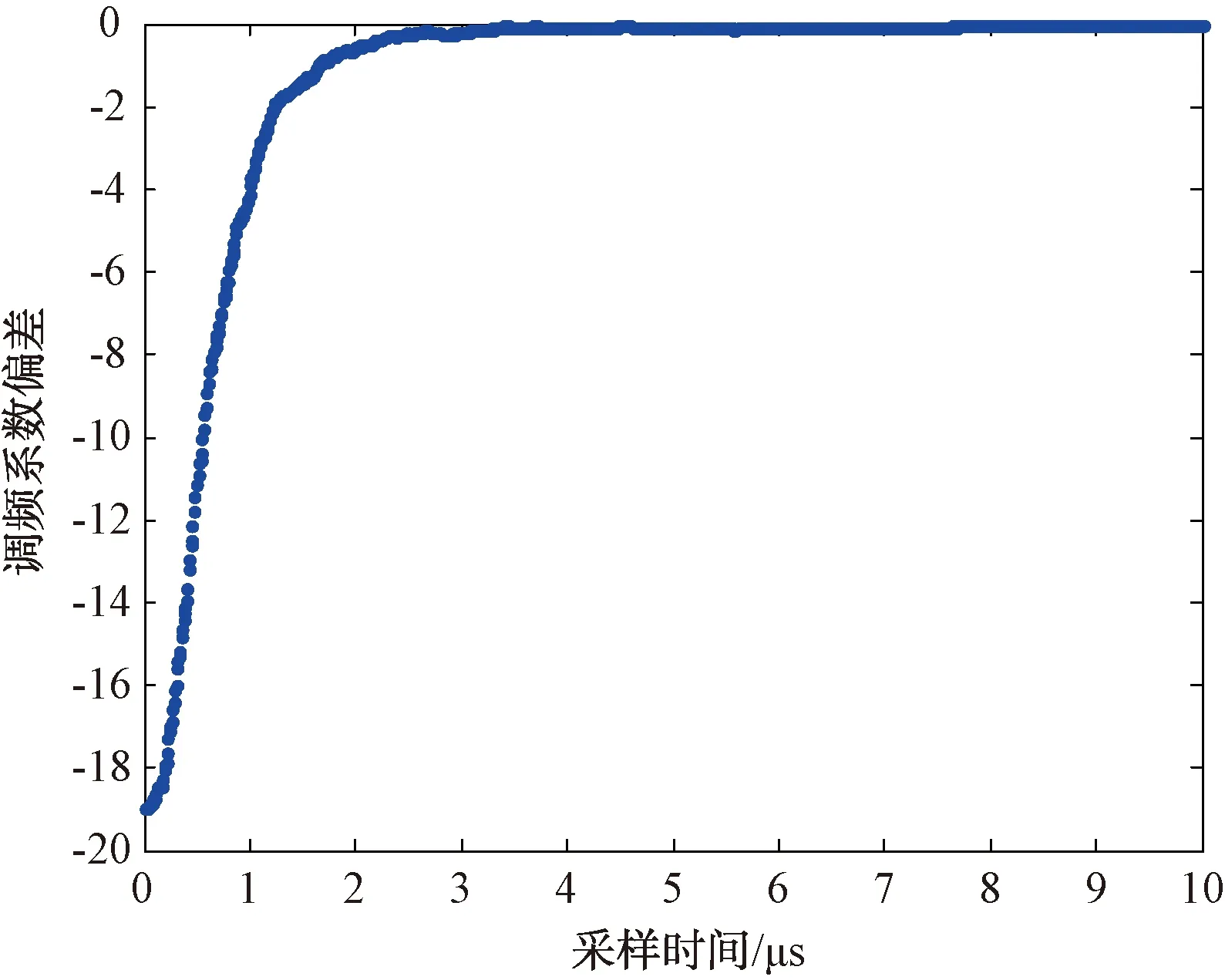
圖7 經過卡爾曼濾波的LFM信號調頻系數誤差曲線

通過以上仿真還可以看出，隨著迭代次數的增多，估計值的誤差將減小，即誤差隨著脈寬增加而減小。LFM信號的脈寬一般大于5 μs，對信號的采樣點數為1 000個以上即可確保測量精度，所以應選擇采樣頻率為500 MHz以上的ADC。對于固定載頻的雷達脈沖信號，可以看作是調頻系數K=0的特殊情況，因此改進的IFM系統也能夠對固定載頻信號進行測量。

4 結束語

通過對基于卡爾曼濾波的改進IFM系統的仿真和分析，表明該方法可以有效測量LFM信號的載頻和調頻系數，并且具有參數估計精度高、實時性好的特點；由于卡爾曼濾波的特性，在脈沖前段存在一定的震蕩，造成了較大測頻誤差，但是可以通過事后的信號數據整理分析來消除震蕩噪聲，不會影響對信號特征的判斷。但在建模過程中，沒有考慮信噪比和同時到達信號的影響，這是下一步需要研究完善的內容。