基于采樣數據的一階多自主體系統的平均一致性跟蹤

顧曉雨,李 力

(中國船舶重工集團公司第七二三研究所，江蘇 揚州 225101)

0 引 言

作為多自主體系統分布式協調控制中的最重要和基礎的問題，多自主體系統的一致性問題因為其在多個領域的廣泛應用而備受關注。多自主體系統的一致性問題主要應用于分布式估計、傳感器網絡的數據融合、無人機的編隊控制、計算機網絡的資源分配[1]等。一致性，即自主體通過與鄰居自主體相互通信交換信息，最終所有自主體的狀態都達到一致。已有的文獻從自主體的模型、時延、拓撲結構、控制策略等角度研究了多自主體系統的一致性[2]。

本文中研究的平均一致性跟蹤問題要求所有自主體的最終狀態跟蹤自主體參考輸入的平均值。平均一致性跟蹤問題顯然不同于平均一致性問題，傳統的平均一致性問題要求自主體最終狀態收斂到自主體初始狀態的平均值。Freeman[3]等分別比較了針對解決靜態平均一致性跟蹤問題的比例平均一致性算法和解決動態平均一致性跟蹤問題的比例積分平均一致性算法，并得出結論：比例積分算法對于常數參考輸入和變化緩慢的參考輸入具有更好的效果。受文獻[3]的啟發，Bai[4]等分析了針對常數參考輸入的比例積分平均一致性跟蹤算法的結構特點，并利用內部模型原理將比例積分平均一致性算法拓展到更一般的情況，使自主體可以跟蹤幾類時變的參考輸入。對于具有常數參考輸入的一階多自主體系統，Shan和Liu[5]考慮了部分自主體缺少參考輸入的平均一致性跟蹤問題，并給出了相應的算法。利用廣義奈奎斯特判據，分別給出了在對稱連通拓撲下，自主體有無通信時延的收斂條件。Shao和Tian[6]針對具有非匹配參考輸入的一階多自主體系統提出了平均一致性跟蹤算法，但是該算法要求所有自主體知道自主體的數量以及所有的參考輸入。

在實際應用場景中，自主體常常因為間歇通信和受限的感知能力而只能周期性地相互通信，最終導致離散或者采樣數據的情況。基于采樣數據的一致性問題引起了研究者的廣泛興趣，并應用代數圖論、矩陣論和隨機矩陣的性質等方法研究了各種限制情況下的一致性問題。現有的研究結果表明，采樣數據控制策略不僅可以極大地減少通信損耗，還可以提高系統對于由系統連接故障和傳輸時延引起的切換拓撲的魯棒性。然而，基于采樣數據的一致性跟蹤效果與采樣間隔密切相關。

受前人研究的啟發，我們提出并分析了2種情況下的基于采樣數據控制的比例積分平均一致性跟蹤算法。第1種情況是所有自主體都具有常數參考輸入，第2種情況是部分自主體有常數參考輸入而剩下的自主體沒有常數參考輸入。利用矩陣論的知識，給出了第1種情況在平衡拓撲下收斂到平均一致性跟蹤的充要條件。相應地，針對第2種情況，運用頻域分析的方法給出了連接拓撲為無相連通拓撲下漸進達到平均一致性跟蹤的充分條件。

1 問題描述

1.1 自主體模型

本文研究的一階自主體系統的模型如下：

(1)

式中：xi(t)∈R和ui(t)∈R分別是自主體i的狀態和控制輸入。

本文的目標就是設計一種控制算法，使得對于任意的參考輸入φi,i=1,2,…,n，有：

(2)

即所有自主體漸進達到平均一致性跟蹤。

1.2 需要引理

引理1：對于n階方陣M，N，P，Q，如果MP=PM，那么：

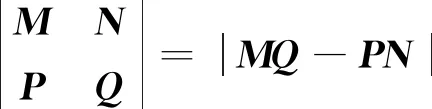
(3)

引理2：對于如下的復系數多項式：

g(s)=s2+(ξ1+iσ1)s+ξ0+iσ0

(4)

式中：ξ1，σ1，ξ0和σ0為常實數。

當且僅當ξ1>0和ξ1σ1σ0+ξ12ξ0-σ02>0成立時，g(s)是穩定的。

2 主要結論

2.1 匹配參考輸入的平均一致性跟蹤

在許多應用場景中，因為數字傳感器和基于計算機的控制，盡管自主體的模型是連續的，自主體的控制器只有在離散采樣時刻獲得采樣數據。為了實現平均一致性跟蹤，考慮一種在離散采樣時刻獲得采樣數據并且控制輸入是基于零階保持器的平均一致性跟蹤算法。假設采樣周期是T=tk+1-tk，提出如下的分布式算法：

(5)

式中：φi∈R和ηi∈R是自主體i的常數參考輸入和內部狀態；在平均一致性跟蹤算法(4)中，ηi(t)的作用是消除自主體的跟蹤誤差；γ>0，kP>0和kI>0是控制增益；xi(tk)和xj(tk)均為在采樣時刻tk獲得的狀態信息。

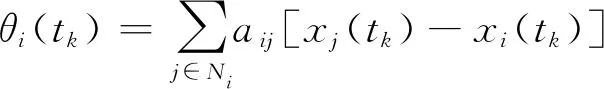
(6)

其中f(t)定義如下:

f(t)=kIθi(tk)(t-tk)+ω

(7)

通過計算得到在算法(4)下的多自主體系統(1)的閉環形式為：

(8)

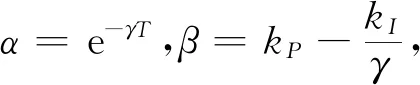
(9)

接下來,針對基于采樣數據的模型(8)，給出相應的結論。

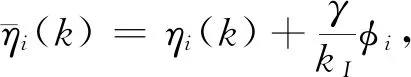
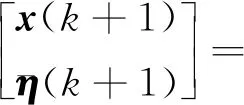
(10)

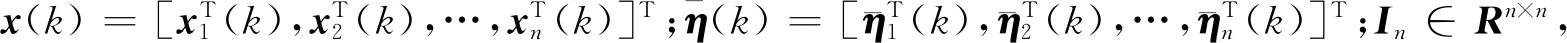
接下來，推導多自主體系統在平衡且強連通拓撲下達到平均一致性跟蹤的條件。

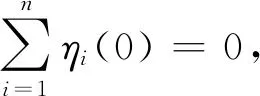
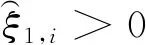
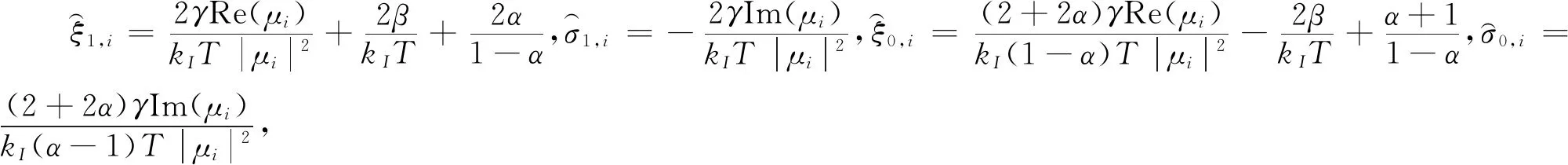
證明：首先分析一階多自主體系統(9)的收斂性。

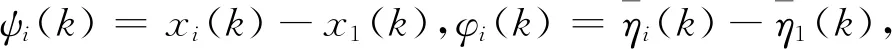
令ψ(k)=[ψ1(k),…,ψn(k)]T，φ(k)=[φ1(k),…,φn(k)]T，z(k)=[ψT(k),φT(k)]T，可得：

z(k+1)=Δz(k)

(11)

式中：

對拉普拉斯矩陣L進行基本行變換和列變換：

(12)

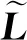
下面分析下列方程的根的情況:

det(λI2n-2-Δ)=0

(13)

根據引理1，式(12)等價于：

det{(λ-α)(λ-1)In-1+[β(λ-1)·(1-α)+

(14)

方程(14)等價于：

(1-α)+kIT(λ-1)+kI(1-α)T]}=0

(15)

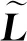
接下來，考察下列方程的根：

(λ-α)(λ-1)+[β(λ-1)(1-α)+

(16)

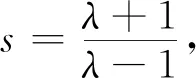
(17)

根據引理2，當且僅當定理1中的(1)和(2)成立時，方程(17)的根都在左半復平面，即在連接拓撲滿足假設1的情況下，一階多自主體系統漸進達到平均一致性跟蹤。

第2步，證明最終達到一致的決策值是常數參考輸入的平均值。由先前的證明可知，一階多自主體系統已經漸進達到了一致，即當k→∞時，x1(k)=x2(k)=…=xn(k)，對于i=1,…,n，有：

(18)

即:

(19)

可以得到：

(20)

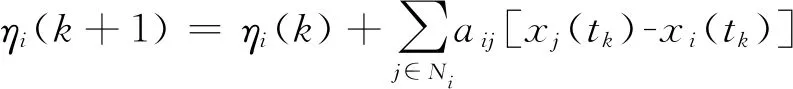
η1(k)+η2(k)+…ηn(k)=η1(0)+η2(0)+…ηn(0)

(21)

2.2 非匹配參考輸入的平均一致性跟蹤

在實際工程應用場景中，多自主體系統中只有部分自主體獲得了參考輸入，而剩余的自主體沒有參考輸入。Shan和Liu[5]研究了連續通信中一階多自主體系統的平均一致性跟蹤問題，所以我們在這部分研究了在采樣數據控制下的情形。

針對第2種情況，將算法(4)修改成了如下形式：

(22)

其中當i=1,…,m時，δi=1；而當i=m+1,…,n時，δi=0。控制目標表示如下：

(23)

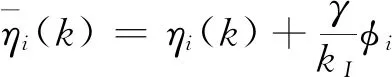
(24)

(25)

得到上述系統的特征方程：

(26)

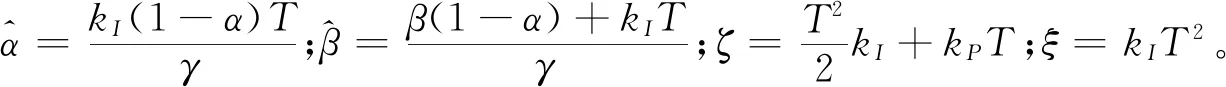
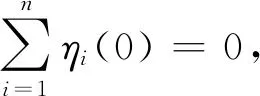
(27)

(28)

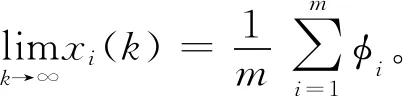
證明：根據引理2和文獻[5]中定理1的證明，方程(19)在z=1處有1個單根。當z≠1時，通過計算可得：

令：

(29)

需要證明F(z)根的模都小于1。根據文獻[7]中的廣義奈奎斯特判據，如果對于ω∈(0,π)，ρ(L)Co(0∪gl(ω),l=1,2)沒有包含(-1,j0)點，則F(z)的零點都在以原點為中心的單位圓內。對于對稱圖，根據拉普拉斯矩陣的定義，可知L=LT≥0。根據文獻[8]中的引理4，可以得到：

ρ(L)Co(0∪gl(ω),l=1,2

(30)

如果ρ(L)Co(0∪gl(ω),l=1,2)沒有包含(-1,j0)點，F(z)的零點除了1個在z=1以外，其余的根都在以原點為中心的單位圓內。剩下的證明過程類似于定理1，在此不再贅述。

3 仿真實例

在這部分，提供了數值仿真以驗證前面得到的理論結論的有效性。

首先考察了第1種情況由4個自主體構成的一階多自主體系統，其通信拓撲是平衡且強連通的，如圖1所示。

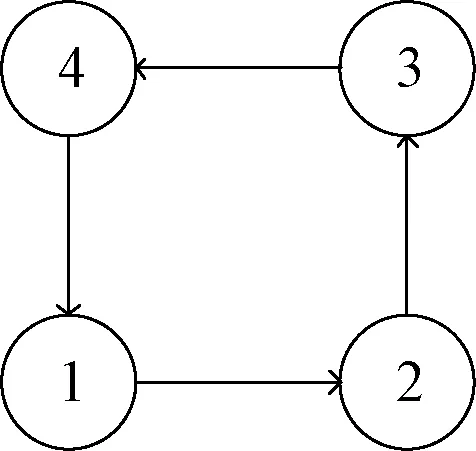
圖1 平衡且強連通拓撲

圖2 自主體的位置

接下來考察第2種情況中由4個自主體構成的多自主體系統，其通信拓撲是對稱連通拓撲，見圖3。

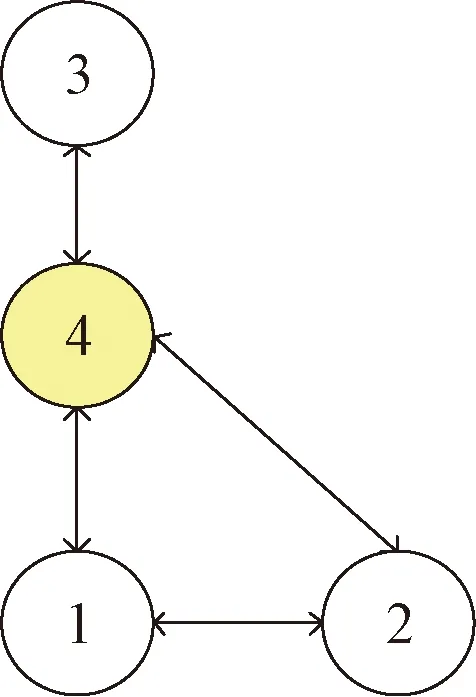
圖3 對稱連通拓撲

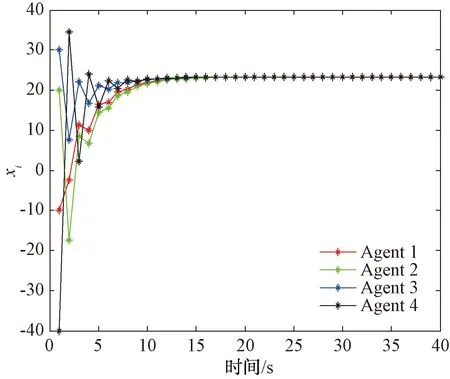
圖4 自主體的狀態

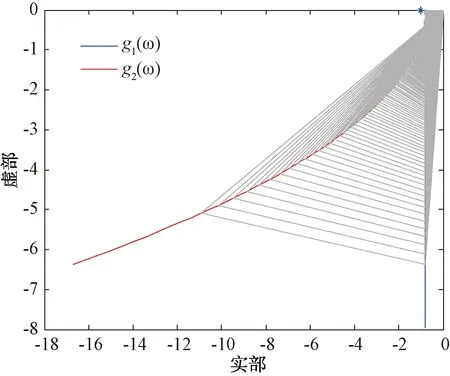
圖5 奈奎斯特曲線ρ(L)Co(0∪gl(ω),l=1,2)

4 結束語

本文對于具有常數參考輸入的一階多自主體系統提出了基于采樣數據的比例積分平均一致性跟蹤算法。首先運用矩陣論和圖論的知識論證并給出了多自主體系統在平衡且強連通拓撲下達到平均一致性跟蹤的充要條件。然后針對部分自主體缺少參考輸入的情況，提出了改進的平均一致性跟蹤算法，并根據頻域分析方法給出了多自主體系統在對稱連通拓撲下達到平均一致性跟蹤的充分條件。