排水泵站整流底坎參數優化

李志祥，馮建剛，錢尚拓，徐 輝,

（1. 河海大學水利水電學院，南京 210098；2. 河海大學農業科學與工程學院，南京 210098；3. 西藏農牧學院水利土木工程學院，林芝 860000）

0 引 言

排水泵站易受地形地質條件限制和周圍建筑約束，進水建筑物布局緊促，難以達到泵站設計規范要求的占地面積和布置形式。緊湊的布置方式使得泵站進水建筑物內常常存在回流、漩渦、偏流等不良流態，進而影響水泵進流條件，引起水泵性能下降，造成汽蝕、機組振動等問題，嚴重影響泵站的安全穩定運行[1]。為此，在排水泵站前池設置整流措施，改善進水建筑物內的不良流態，對保障泵站安全運行具有重要意義。

底坎作為廣泛應用的整流措施，能夠有效改善前池流態，通過挑流及坎后的漩滾作用，破壞前池兩側回流形成條件，促進水流充分紊動擴散，從而在進水池入口處獲得滿意的流速分布[2]。該措施施工簡單、經濟易行、效果顯著。曾昊等[3]在泵閘工程應用一字型底坎，討論一字型底坎對出流流態的影響，分析其參數變化的影響效果；羅燦等[4]采用計算流體力學（Computational Fluid Dynamics，CFD）數值模擬技術研究前池底坎整流措施，探討了底坎位置、高度及頂寬對整流效果的影響，提出前池底坎設置方案；馮建剛等[5]針對泵站前池的布置特點，提出了導流墩結合底坎的組合式整流措施，對正向、側向進水泵站前池流態均有較好的改善效果。目前，研究者對前池底坎整流措施水力優化設計研究較少，且通常采用控制變量法比較設計參數對流場水力特性的變化，略去底坎設計參數同時變化對三維流場水力特性的耦合作用。

響應曲面模型能通過試驗獲得響應變量與設計變量之間的多項式函數關系，從而提高優化效率[6]。即通過擬合目標變量與設計變量之間各種階數的模型，描述二者之間存在的未知、復雜函數關系，由此作為二者之間真實函數關系的一種近似，并對其進行模型分析[7-9]。資丹等[10]將其應用于泵站進水池垂直吸水管布置優化分析中，給出淹沒深度、最優懸空高、后壁距的最優組合；高學平等[11]應用響應曲面法建立以抽水蓄能電站進/出流時的流量分配等多個水力指標作為目標函數，擬合了以擴散段長度等作為設計參數的響應模型。因此，可以考慮將響應曲面優化設計方法應用到前池整流措施參數優化分析中，利用其可以給出設計變量與目標值之間函數關系的優勢，找出最優設計，降低數值計算工作量，提高計算效率。

針對底坎整流措施體型及布置參數多目標優化問題，本文擬考慮坎高、坎距的耦合影響，提出結合信息量權數法的響應曲面模型，并對整流底坎的高度和布置位置進行參數優化。建立表示流場水力特性的綜合目標函數與整流底坎設計參數的多項式函數關系式，得出最優底坎體型及布置參數，改善泵站進水建筑物內流場流態，以期為同類泵站的整流措施設計和優化提供參考。

1 排水泵站數值模型與驗證

1.1 排水泵站計算模型建立

圖1是典型的排水泵站結構圖[12-13]，泵站結構設計參考上海新宛平泵站及文獻[12]中的泵站布置形式，其典型特征表現為水流正向進流，前池擴散角大，水泵機組對稱布置。泵站進水建筑物總長4.1 m，包括引渠段、擴散段、前池、進水池、喇叭口和吸水管。引渠段長度為2.0 m，前池擴散角為44°，吸水管喇叭口直徑為97.5 mm，單個機組進水池寬度D為270 mm。前池水位H為300 mm，單泵排流量為5 L/s。

1.2 排水泵站水力性能的數值模擬方法

基于雷諾時均納維-斯托克斯方程（Navier-Stokes equations，N-S方程）和剪切應力傳輸模型（Shear Stress Transfer，SST），對泵站進水建筑物內水流流動情況進行模擬。SSTk-ω模型能預測泵站內部在逆壓梯度作用下出現的水流分離流動現象及回流區范圍[14]。控制方程基于有限體積法進行離散，計算時離散格式對流項采用二階迎風格式，擴散項和源項采用中心差分離散格式，數值求解方法采用半隱式方法SIMPLEC算法[15-16]。自由液面采用剛蓋假定法，數值計算的定解條件如下：泵站引渠進口設置為正交速度進口，計算域出口設置在吸水管末端，采用自由出流的方式，進水建筑物內自由液面處設為剛蓋假定法的對稱邊界，其他固體邊界設置為標準式壁面函數下的無滑移壁面邊界。為保證網格質量，采用ICEM CFD（The Integrated Computer Engineering and Manufacturing code for Computational Fluid Dynamics）對泵站進水建筑物進行六面體結構化網格劃分，對比5套粗細不同網格方案（網格總量為62～285萬），綜合考慮計算效率和精度，最終選取網格數量為1 363 996[17]。圖2為泵站數值模擬的計算模型示意圖。

1.3 排水泵站計算模型驗證方法與結果

1.3.1 排水泵站物理模型試驗方法

針對泵站進水建筑物無整流措施計算結果，通過對比數值模擬和物理模型試驗的表面流線及流速分布結果，分析本文構建的泵站數值模型及模擬方法的可靠性。

圖3是泵站試驗模型照片，物理試驗模型按照圖1泵站結構圖1:1建立，采用全透明泵站進水建筑物自循環開敞式系統，包括引渠段、前池、進水池、吸水管、出水池、管道離心泵、回水管、進水箱、整流柵等。圖1所示的流速測點由光電流速儀進行量測，光電流速儀的精度為1.0%。泵排流量由安裝于水泵出水管上的轉子流量計進行量測，精度為±2%。試驗中，前池進水池水位由水位測針量測，水位測針采用南京水科院制作的高精度復式測針，測針讀數誤差為±0.1 mm。

1.3.2 結果與分析

圖4是數值模擬和物理試驗獲得的表層流線圖。從試驗流線可知，前池兩側存在大范圍回流區，其回流范圍從擴散段中部延伸至進水池入口，回流中心點位于擴散段末端附近，與外側邊壁的垂直距離約為0.8D。此外，邊緣進水池隔墩背水側也存在著較大范圍的漩渦，漩渦分布在隔墩頭部和吸水管間。數值模擬所得的流線圖反映的前池兩側回流范圍、回流中心、形態及進水池隔墩背水側漩渦與試驗現場觀測的流態吻合度很高，表明數值模擬能很好預測到前池、進水池內存在的回流、漩渦等不良流態。

圖5為擴散段末端面層的流速分布圖。為了方便比對，將擴散段末端位置各點x方向流速u與引渠段進口平均流速um相除，實現流速無量綱化，并作為縱坐標；橫坐標為y/D，D是進水池寬度，中間位置y/D=0，左側邊壁橫坐標為-2.28。由圖可知，u/um在y/D=0附近有較大值，數值模擬與試驗測得的較大流速均出現在前池中部。數值模擬結果能夠預測到水流受到逆壓梯度力的影響在前池兩側形成較大范圍的回流區，總體流速分布規律與試驗值所示基本一致。擴散段末端面層流速分布模擬值和試驗值的R2為0.98，均方根誤差（Root Mean Square Error，RMSE）為0.06，進一步表明本文泵站數值模型及其水力特性數值模擬方法的可靠性，可以用于后續的整流底坎參數優化計算。

2 基于數值模擬方法的泵站整流底坎參數優化

2.1 泵站底坎整流參數設計

底坎整流作為流體分離流動理論在水利工程上的應用，泵站進水建筑物內流場流態復雜，存在高曲率大變形的流動，在既定泵站設計尺寸和運行條件情況下，底坎的整流效果主要受坎高、坎厚和底坎的位置影響[18]。而前人的研究成果表明[2-4,18]，當整流底坎厚度在坎高某倍數范圍變化不會對流態產生顯著影響。所以，本次數值方案僅考慮泵站固定流量下，底坎的坎高和布置位置對泵站進水建筑物水頭損失、渦量、流速分布的影響。

為詳細研究坎高、布置位置取值對目標函數的影響，依據前置試驗[19]，對兩者最優范圍進行適當的縮小，坎高、布置位置的取值范圍：坎高h取0.1H～0.34H，底坎布置位置d取4.5D～6.5D。這里底坎布置位置即坎距，指底坎迎水面到吸水管中心線的水平距離，如圖1和圖2所示。樣本空間采用析因設計獲得，相比其他試驗設計方法，析因設計在參數取值范圍內采樣更加均勻且獲得信息量巨大，能準確估計出坎高、布置位置的主效應及交互影響。如果采用Design-Expert自帶的外切中心復核設計等試驗設計方法，系統會根據研究因素數目（本文為2），自動給出13組樣本，其中有4組樣本為重復樣本，此時，因為計算樣本較少而難以建立精度較高的響應曲面模型。更多水平數的設計會使得優化工作量呈現指數式增長，而計算精度得不到顯著地提升。綜合考慮優化計算的成本及效率，在坎高、坎距的取值范圍均勻選取5個點，進行二因素五水平自由組合，得到25個樣本空間，如表1所示。采用本文構建的數值模型和數值模擬方法對該設計樣本，進行CFD數值計算，得出整個泵站進水系統計算域的水力損失系數、控制斷面的流速不均勻系數和喇叭口渦量特征值。

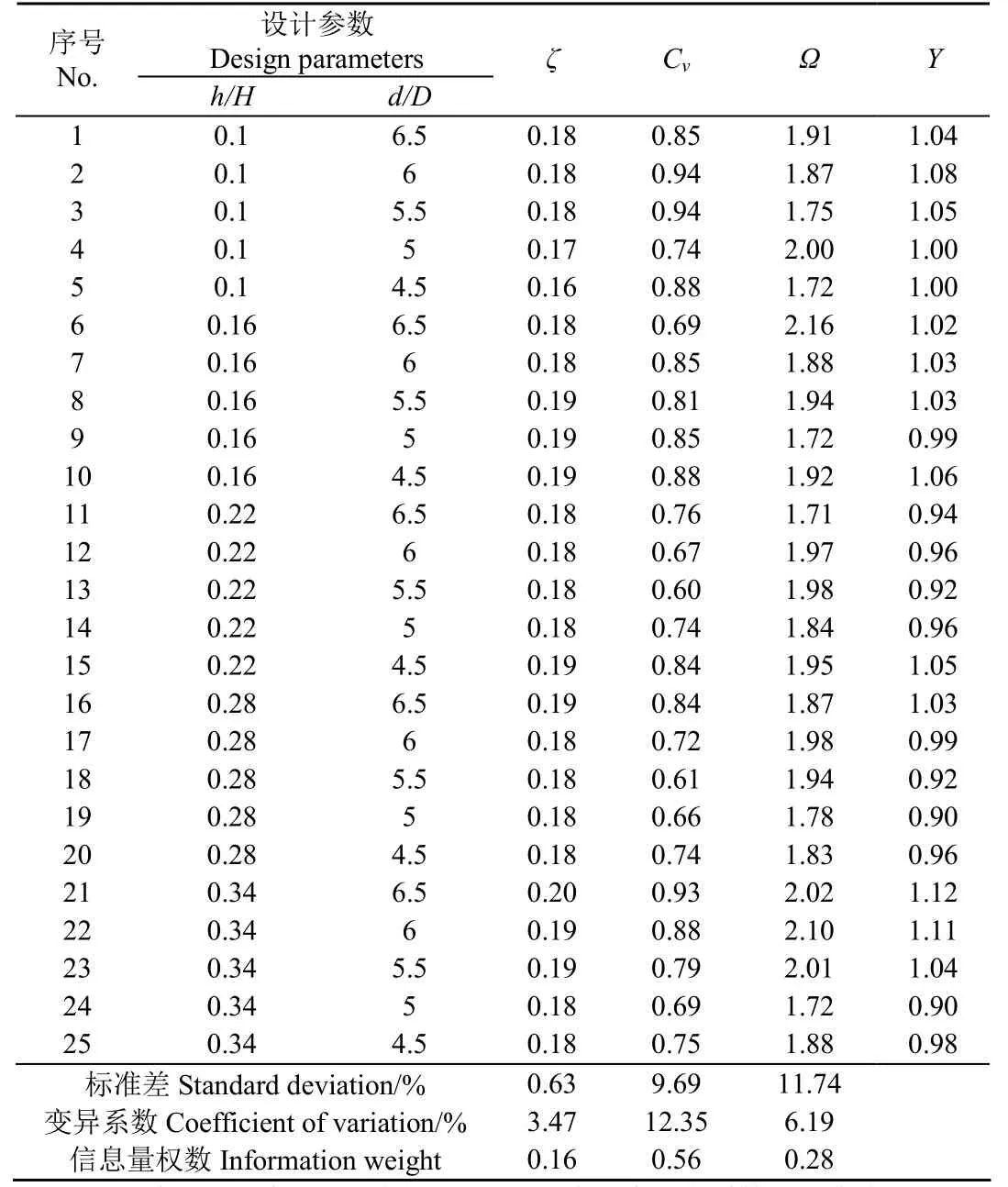
表1 泵站底坎整流參數設計及整流效果數值模擬結果Table 1 Parameter design of rectification bottom sill in pumping station and numerical simulation results of rectification effect

2.2 水體流態評價指標計算方法

泵站實際運行狀態中，進水系統內通常會存在回流、漩渦等不良流態，各個進水池進流不夠均勻平順，會對水泵機組的高效穩定運行造成影響。水力損失、流速均勻度、速度加權平均角度等常作為定量描述泵站進水系統流態的評價指標[10,16]。本文對這3個指標作部分修改。

水力損失系數可以表征泵站運行效率，高效率運行的泵站水力損失較小。采用水力損失系數無量綱數（ζ）定量描述泵站效率，其計算公式如下[11]：

式中hw為水力損失，m；z為計算斷面的位置水頭，m；為計算斷面平均壓力，Pa；為計算斷面平均速度，m/s；ρ為20℃液態水的密度，kg/m3；g為重力加速度，m/s2；其下標數字1和2分別代表計算域吸水管進口和出口。

流速不均勻系數（Cv）為進水池入口流速標準差與平均流速的比值，常用于評價進水池入口流速分布均勻性的指標。本文采用Cv定量表征泵站進水系統的流場均勻性。優良的泵站進水建筑物水力設計，其前池能夠平順均勻地將水流輸送至各個進水池，進水池入口流速大小相近，流速方向均為入口截面法方向，此時流速不均勻系數接近0。Cv計算公式如下[10]：

式中m為進水池進口截面的選取單元個數；ui為各單元i的法向速度，m/s。

漩渦是泵站進水建筑物內流場常見的不良流態，可利用渦量描述漩渦運動。在直角坐標系下，渦量可分為x、y、z3個方向分量，許多學者往往選取某一最能反映該流場特征的漩渦運動分量來分析渦量場特點[10]。使用分渦量就會略去其他方向的渦量值，不能很好反映真實的渦量場信息，為此選用合渦量ω（s-1）表示某處的渦量值大小。環量計算可以描述閉合曲線內的水流旋流程度，而且可以反映該處的漩渦運動強度和漩渦核心大小[20]。本文選取喇叭口截面計算合渦量的平均值，選取其進口圓周線作為積分曲線，計算喇叭口水流預旋及漩渦強度情況。為突出吸水管喇叭口附近渦量特征，將喇叭口合渦量均值與速度環量相乘，采用無量綱形式分析喇叭口附近的漩渦分布特點。本文的評價渦量場優化程度的量化指標可采用式（4）進行計算。

2.3 基于信息量權數法的多目標優化求解方法

底坎的整流效果評價指標有水力損失系數、流速不均勻系數和喇叭口渦量特征值3個目標，對于該類多目標優化求解主要有2種：1）以約束法、權重法或隸屬度法將多目標問題轉化為單目標進行求解；2）采取多目標進化算法進行求解，生成一系列非劣方案[21]。多目標進化算法往往會伴隨著優化對象的大量迭代計算，每次的迭代都需要研究人員重新建模計算，整個優化過程將變得繁雜，耗時過長。所以本文這3個評價指標揉合在一起，賦予不同的權數，凝練為單個綜合目標，使得問題變得簡單易行[8-10,22]。其中權數的確定是多目標優化方法最為關鍵的一環，直接影響綜合評價的結果，改變目標優劣順序[23]。信息量權數法[24]是根據評價指標分辨信息多少，將評價目標的這種差異加以量化來確定的權數，可以比較不同評價指標間的優劣，用于處理多目標決策問題。因此，本文采用信息量權數法，將水力損失系數、流速不均勻系數和喇叭口渦量特征值3個評價指標的變異系數歸一化處理，確定權數。具體步驟如下：

1）設評價體系里包含K個指標Xk（k=1,2,3,…,K）；每個指標含有n個樣本。

2）計算標準差

3）計算各指標的變異系數

4）將Vk歸一化處理得到各個指標的信息量權數

5）最終形成綜合目標函數形式為

式（5）～式（9）中n為樣本個數；為n個樣本指標Xk的平均值；Sk、Vk和Wk分別為指標的標準差、變異系數和信息量權數；Y為綜合目標函數，由ζ、Cv和Ω三者乘以各自不同的權數形成。理想的整流效果是泵站進水系統水力損失系數極小，水流進流平順均勻，吸水管喇叭口不存在預旋，進水池不存在附壁渦、附底渦等不良水力現象。Y值越小，泵站前池底坎整流效果越好，泵站運行效率越高。

2.4 靈敏度分析

Sobol’法的中心思想是將函數分解為遞增項之和，通過采樣計算其總方差和各項偏方差，以求得各參數靈敏度[25]。相比直接求導法等局部靈敏度分析方法，Sobol’法作為全局靈敏度分析方法，不僅可以檢驗單個參數變化對模型結果的影響，還可考察多個設計參數同時變化對模型的影響。因此，本文基于Sobol’法對建立的響應曲面模型進行全局靈敏度分析，確定設計參數間交互作用。

3 結果與分析

3.1 綜合目標函數構建

不同坎高和坎距設計下，整個泵站進水系統計算域的水力損失系數、控制斷面的流速不均勻系數和喇叭口渦量特征值如表1所示。h/H為底坎高度與前池水深的比值，d/D為底坎到吸水管中心線的水平距離與泵站進水池單個水泵機組進水池寬度的比值。根據上文信息量權數的求算辦法，對表1中數據進行計算，確定變異系數及相應的信息量權數，最終形成加權函數如下：

式中Y為綜合目標函數；ζ為水力損失系數；Cv為流速不均勻系數；Ω為喇叭口渦量特征值。

3.2 綜合目標函數的響應曲面模型構建

前池底坎的設置改變泵站進水系統的流態，產生的漩滾和挑流作用，使得前池水流紊動劇烈且存在高扭曲大變形的流動，目標函數與影響因素之間的關系因而反映為高度非線性。如果采用一階或二階多項式擬合這種非線性關系，則難以反映真實關系，擬合精度難以保證，而更高階數的多項式雖然在計算域內可能會有更好的擬合效果，但是計算量顯著增大，形式復雜，故不采用。本文應用響應曲面模型對表1中的數據進行擬合，建立反映相對坎高、相對坎距與Y之間影響關系的三次多項式數學方程如式（11）所示，為方便起見，采用x1代替h/H，x2代替d/D。

式中x1為相對坎高；x2為相對坎距。

響應曲面模型的誤差分析見圖6，圖中各點分布均貼近1:1線，表明其擬合效果較佳。綜合目標函數的R2為0.86，RMSE為0.02，可知響應曲面模型精度較高，擬合的三階多項式能較好地預測底坎坎高、坎距與目標函數的關系。

3.3 泵站整流底坎參數靈敏度分析

響應曲面模型設計參數的靈敏度分析結果見表2。一階及總體全局靈敏度系數較大，系數范圍為（0.42～0.58），可知建立的響應曲面模型受兩個設計參數的變化影響大。其中，相對坎高的一階全局靈敏度系數大于相對坎距，說明相對坎高對模型影響程度高于相對坎距。一階全局靈敏度與總體全局靈敏度系數差值大，兩設計參數所求得的系數差值均超過其一階全局靈敏度系數的20%，表明設計參數間存在顯著的交互作用。

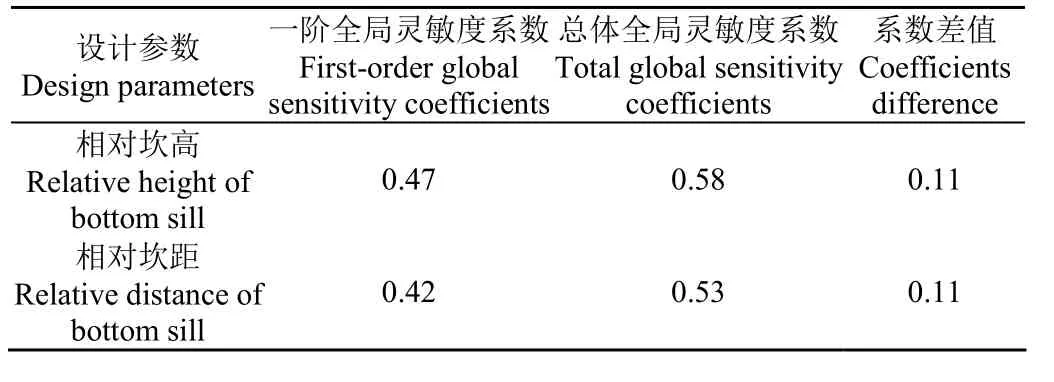
表2 泵站整流底坎參數靈敏度分析Table 2 Sensitivity analysis of design parameters of bottom sill in pumping station

3.4 基于響應曲面模型分析坎高和坎距對綜合目標函數的影響

圖7為坎高、坎距對目標函數的響應，整流底坎的高度、距離對泵站進水系統三維流場的速度場和渦量場的影響顯著。由圖7a三維曲面云圖可知，總體而言目標函數Y隨著相對坎高x1的增大和相對坎距x2的減小，先快速減小后略增大，在研究范圍內存在著最小值。x1在0.26～0.32，x2在4.8～5.2之間時，Y有較小值，泵站進水系統流態有明顯改善。當x1在0.22以下時，目標函數Y隨著x2的變化反應較為平緩，表現為隨著x2的增加，先緩慢下降后緩慢增加；當x1在0.22以上時，目標函數Y隨著x2的增加先緩慢下降后快速增加。反映為當底坎高度小于0.22H時，流場的流態隨坎距的增加先改善后惡化；當底坎高度大于0.22H時，流場的流態隨底坎距離的增加先略有改善后急劇惡化。圖7b顯示相對坎高、相對坎距對目標函數的耦合影響。這2個參數同時變化其耦合效果顯著，兩者交互影響大。如果坎高和坎距這兩個因素之間沒有交互影響，則在響應等高線云圖上，等高線呈現為一族同心圓。反之，如果響應等高線云圖上，等高線發生強烈扭曲，表明二因素交互作用強烈。可見實際上，坎高和坎距同時變化對流場流態的交互影響作用是不可忽視的。

3.5 底坎參數優化

本文以底坎相對高度、相對坎距為優化設計自變量，以綜合函數Y作為目標，利用最速下降法求解綜合目標函數在計算區域內的最小值。目標函數Y在某點的梯度表示在此處的函數值上升速度最快，則該點的負梯度表明在此處的函數值下降速度最快，最速下降法是使用負梯度搜尋函數在某區域的最小值。通過計算，得出目標函數預測值Y=0.90，此時x1=0.29而x2=5.02。根據上述求解的優化參數，進行CFD數值模擬對比有無整流措施對泵站水力性能的影響，如表3所示，采用底坎整流措施后泵站流速不均勻系數減小19.28%，計算域水力損失系數減小5.26%，喇叭口渦量特征值降低了5.76%，3個定量評價指標均有所減小，說明采用該優化設計方法可大大提高流場內的流態。響應曲面模型與CFD數值模擬所得綜合目標函數值的相對誤差為1.30%，可認為得到的響應關系式能滿足精度要求，能反映底坎高度、坎距對泵站進水系統流場流態的影響。

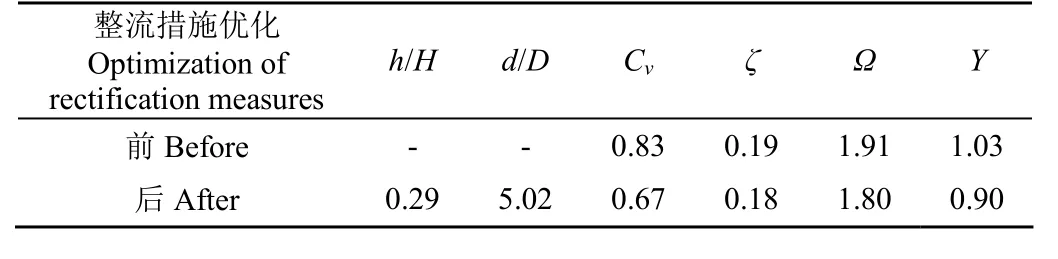
表3 泵站前池整流參數優化前后水力性能對比Table 3 Comparison of hydraulic performance before and after optimization of rectification parameters in the forebay of pumping station

圖8為原始方案和優化方案的中層水流x方向流速云圖。由圖8a可知，水流自引渠流入前池，由于前池擴散角較大，過流面積增大，流速減緩，產生較大的逆壓梯度，使得主流與邊壁脫流，在擴散段邊壁與主流之間形成回流區，回流區甚至延伸至進水池入口。前池回流區的存在會進步壓縮主流真實過流面積使得該處的局部流速甚至大于引渠流速，另一方面，主流收到壓迫集中直沖中間兩個進水池，兩側進水池進水不夠順暢，隔墩處存在明顯背水側漩渦，不利于水泵吸水。從8b圖可知，優化后的底坎整流措施，顯著改善泵站進水建筑物內的不良流態，前池兩側的大范圍回流區顯著縮小，隔墩背水側漩渦完全消失。水體在底坎作用下，相互碰撞、混摻，使得紊動能進一步向前池兩側低動能水體傳遞，該區域的水體獲得相近的流速，促使水流平順均勻地流向進水池。

圖9為機組縱剖面渦量圖，這里渦量為合渦量。無論原始方案還是優化方案的最大渦量值出現在喇叭口內側壁面下方，這是因為進水池內水流從四周繞流進入吸水管，流線彎曲程度大，在流過喇叭口尖端時會產生很強的渦量。對比圖9a和圖9b，優化后的底坎整流措施，有效削弱了喇叭口下方附底渦強度，高渦量區域明顯縮小，且減小了后壁面產生的附壁渦。

4 結 論

應用計算流體力學（Computational Fluid Dynamics，CFD）技術，基于響應曲面模型研究了底坎相對高度、相對距離與泵站進水流態之間的函數響應關系得出以下結論：

1）信息量權數法可對泵站進水系統內速度場和渦量場的多個評價指標進行賦權，形成綜合目標函數來定量表示底坎整流措施對泵站流態的改善效果。

2）以底坎相對高度、距離為設計參數，進行響應曲面優化分析，擬合三次多項式響應面模型的函數關系式，綜合目標函數的R2為0.86，均方根誤差為0.02，模型具有較高精度。基于響應曲面擬合結果，采用最速下降法求解的底坎整流措施最優參數組合的相對坎高為0.29，相對坎距為5.02，所計算的綜合目標函數實際值與估算值相對誤差為1.30%，表明所采用的三次多項式響應面模型能準確描述底坎整流措施設計參數與綜合目標函數之間的關系。

3）基于最佳參數組合對底坎坎高和坎距進行優化，并模擬泵站水力性能，結果表明，優化后泵站流速不均勻系數減小19.28%，計算域水力損失系數減小5.26%，喇叭口渦量特征值降低了5.76%。底坎優化方案前池兩側回流區基本消失，各個進水池水流進流平順，吸水管附近漩渦強度明顯減小，進水建筑物內流態得到顯著改善。表明響應曲面模型可用于泵站整流措施參數優化設計，改善前池、進水池流態，提高泵站的水力效率和運行穩定性。

本文僅以整流底坎的坎高和坎距2個設計參數進行優化，但是，前池整流措施形式多樣，且存在組合應用，后續可對其他組合形式的整流措施進行更多設計參數的優化分析。