流體懸浮及其穩定性探究
劉鎧銘,周亞杰,趙述敏,王紅理
(西安交通大學 物理學院,陜西 西安 710049)
輕質物體能在向上噴射的自由射流柱的邊緣部分處于穩定的懸浮狀態,并在懸浮的同時開始旋轉,稱此現象為流體懸浮. 物體在流體中的懸浮現象是目前備受關注的新興的物理問題,此問題涉及流體力學前沿的相關研究,如Navier-Stokes方程、邊界層理論等. 流體懸浮的應用也很廣泛,比如核領域中國內液體懸浮式非能棒控制系統[1]和國際上較為成熟的液體懸浮式非能動停堆系統[2],現代工業中液質懸浮式永磁多自由度電機,等等.
1 流體懸浮模型
1.1 實驗裝置
由水龍頭接軟管構成供水系統,將軟管出水端固定,固定裝置由2個相同的鐵三角和鐵桿作為支撐,用可轉動的十字夾固定出水口,由磁鐵和鐵塊作為十字夾的穩定裝置,使噴水的角度固定.
1.2 實驗現象
實驗中,將圓柱體靜止地放在自由射流邊緣,脫手后在1 s內,圓柱體會開始旋轉,高度趨于固定值,轉速基本保持恒定.
1.3 模型構建及理論分析
懸浮模型如圖1所示,其中G為圓柱體重力,F1為水流沖力,F2為壓強梯度力,M1為水流黏滯力矩,Mf為空氣黏滯力矩.
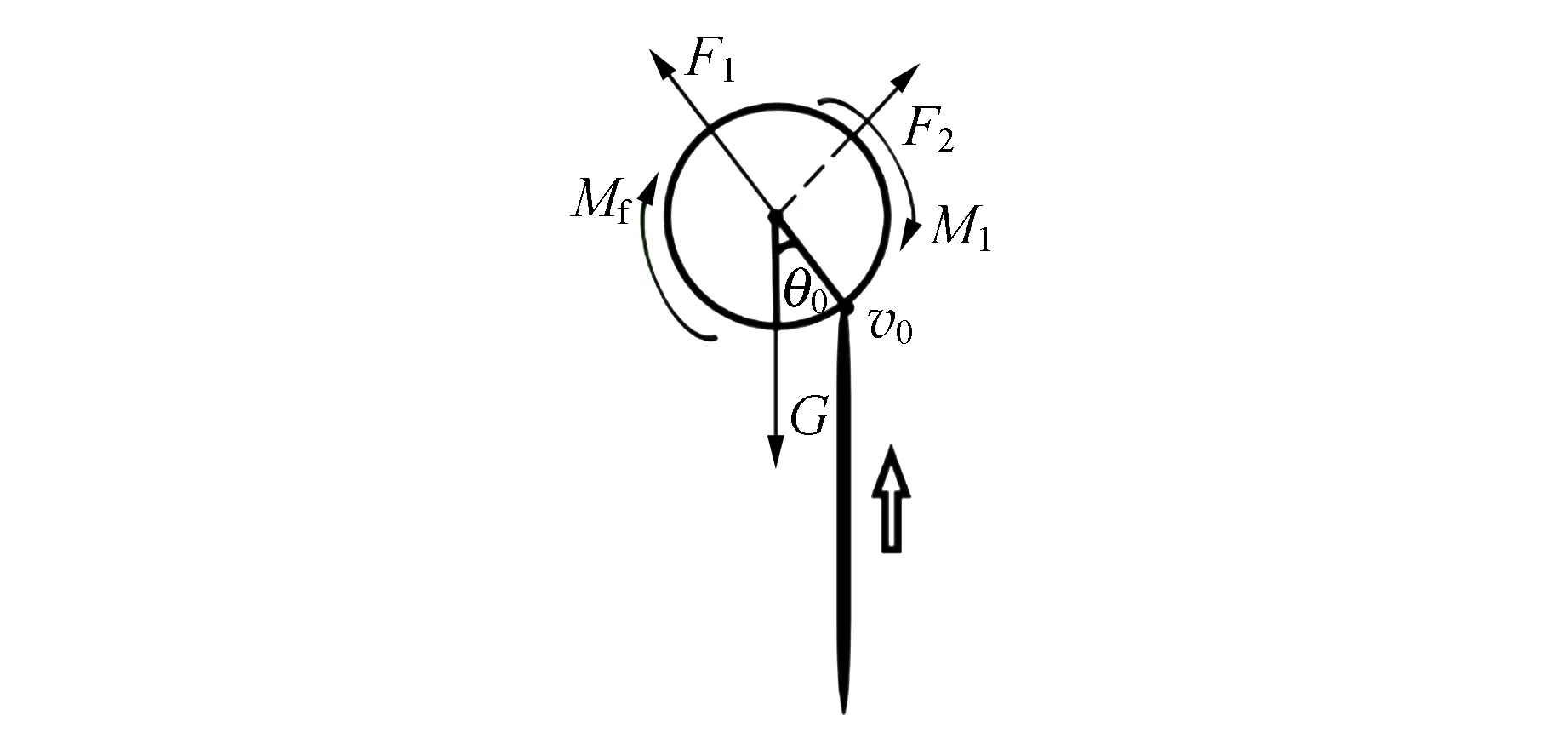
圖1 圓柱體的懸浮模型
圓柱體懸浮時會圍繞平衡點輕微上下振動,振幅近似不變,定義該點為輕質物體的穩定懸浮高度,此時圓柱體受力平衡:
F1+F2+G=0,
(1)
圓柱體穩態轉速近似恒定,圓柱體受到的合力矩
M1+Mf=0,
(2)
無物體懸浮時,水柱的高度為h0. 每秒噴水質量為mt,水流初始速率為vb,懸浮高度處水流速率為v0,由于過輕的物體無法懸浮,而稍重的物體懸浮高度h較低,所以實驗中的vb與v0較為接近,可近似認為水柱的半徑Rw等于水管的半徑Rl,在水柱擊打在圓柱體側面的瞬間,其動量可以分為沿圓柱體橫截面的徑向和法向,其中沿圓柱體徑向的沖量全部轉化為對圓柱體的沖擊力F1,其大小為p0cosθ0,θ0為沖擊面中心點與圓柱體軸心的連線與豎直方向的夾角,稱為偏心角.
F1=p0Scosθ0,
(3)
將p0和S表達式代入(3)式,得:
(4)
式中h為穩定懸浮高度,由于康達效應,圓柱體側面形成繞流,繞流在向上的過程中由于黏滯阻力和重力作用速率會逐漸衰減、寬度增加、厚度逐漸變薄,繞過最高點后速率又逐漸增加、寬度增加、厚度繼續變薄,形成繞流.
先求解二維的速率分布(繞流范圍為平面不規則圓環),由于圓柱體側面左右對稱性,可以近似認為處在同一高度、同一角度、同一厚度處的繞流速率相等,于是可以將二維模型拓展到三維. 設繞流覆蓋角度θ的范圍為2π,寬度為a,達到穩定時,視其為定常流動,任取一流體微元,其所處的厚度為d(θ),速度為v(d,θ),如圖2所示.
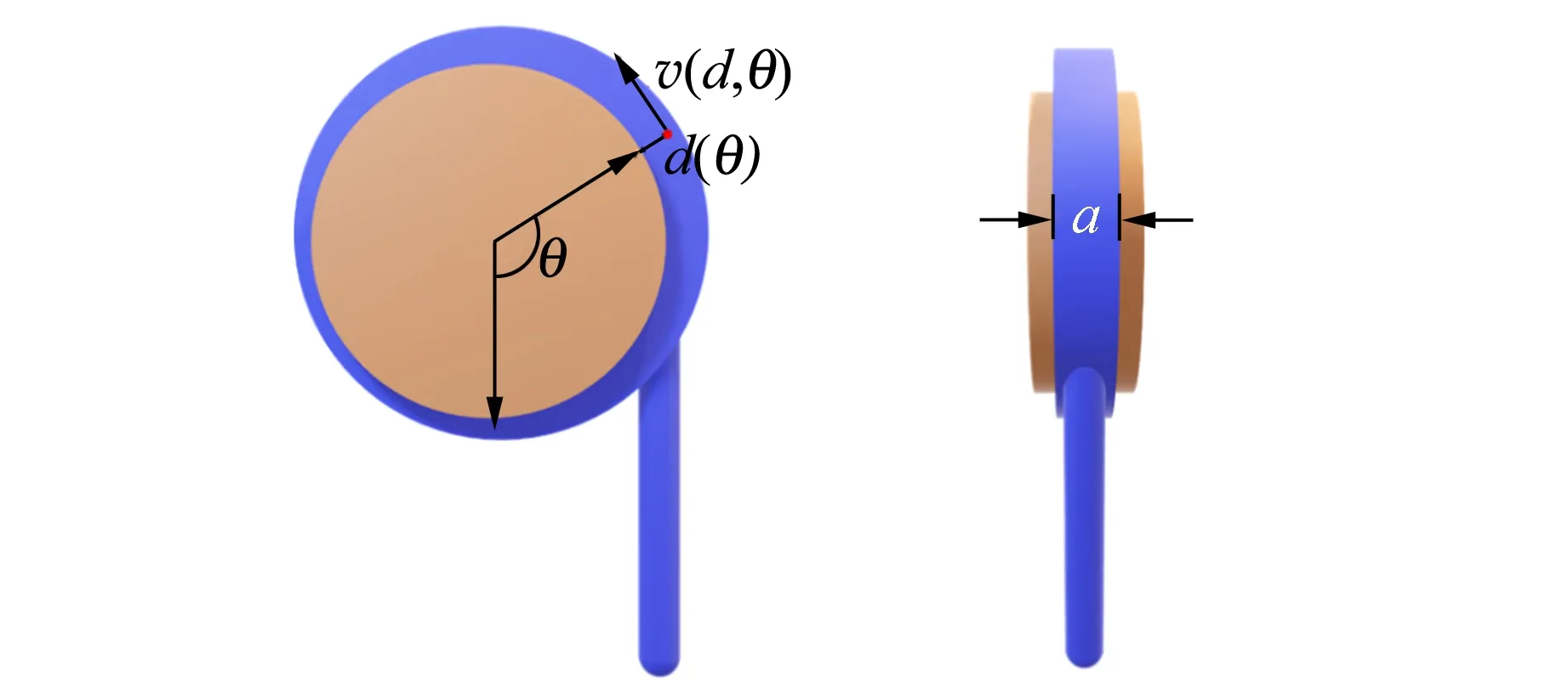
(a)側視圖 (b)俯視圖圖2 圓柱體的懸浮
當整個系統到達穩態時,圓柱體側面任意位置處流體微元的速度和繞流的厚度不隨時間變化,用N-S方程描述繞流系統:
(5)
聯立連續性方程:
引入邊界層理論[1]描述繞流系統,不考慮外層黏滯阻力和無滑移條件,N-S方程可簡化為
使用有限差分法得到微分方程組的數值解,時間步長取0.1 s,空間步長取10-5m,角度步長取2π/100 ,確認初始條件后對時間進行迭代. 當相鄰兩代之間的數據相差小于1%時停止迭代.
對于邊界層內的流動,其雷諾數[2]的數值為
式中,ρ為水流密度,取103kg/m3;v為繞流速度,v<10 m/s;L為特征長度,這里指柱體的直徑,L在10-2m量級;μ為水的動力黏度,在20 ℃時取1.01×10-3Pa·m. 由于雷諾數小于5×105,則可以將邊界層內的流動當作層流來分析,δ表示邊界層厚度,則y處的速度可以寫成
泰勒展開并取一階近似,得:
V(y)=a0V.
將邊界層繞流與外層繞流速率分布結合得到完整的側面水流繞流速度場,如圖3所示.
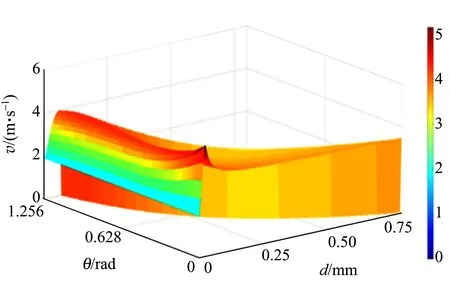
圖3 水流繞流的速度場
圖3中緊貼圓柱體側面的1層水流速度降低不明顯,但水膜的厚度隨圓柱體旋轉變薄,動量和能量的傳遞體現為水流動量層厚度的損失,這部分水的動量和能量變成圓柱體旋轉的角動量和能量. 通過流速場求解壓強分布,邊界層內壓強在垂直于壁面方向存在梯度,滿足動量積分方程[3]:
使用思韋茨解法[1]求解,動量厚度為t,則
U(x)為繞流流速分布,通過前面的有限差分法即可解得. 定義量綱為1的動量厚度
結合流速分布和動量厚度求解出各流體微元的黏滯力分布
對所有與圓柱體直接接觸的流體微元求和,得到黏滯力矩為
(6)
當邊界層非常薄時,可忽略垂直于固體邊界的流速,則邊界層內的N-S方程可以簡化為
(7)
可得圓柱體側面的壓強分布p*(并且考慮繞流附加重力),對所有微元求和得到壓強梯度力為
(8)
通過水流速度場可以求解得到空氣流速場.
圖4是空氣流速場在5 min內變化趨勢,空氣黏滯力矩在10-9N·m量級,圓柱體轉動慣量在10-5kg·m2量級,因此可忽略空氣黏滯力矩.
平衡方程可以寫成:
F1+F2+G=0,
(9)
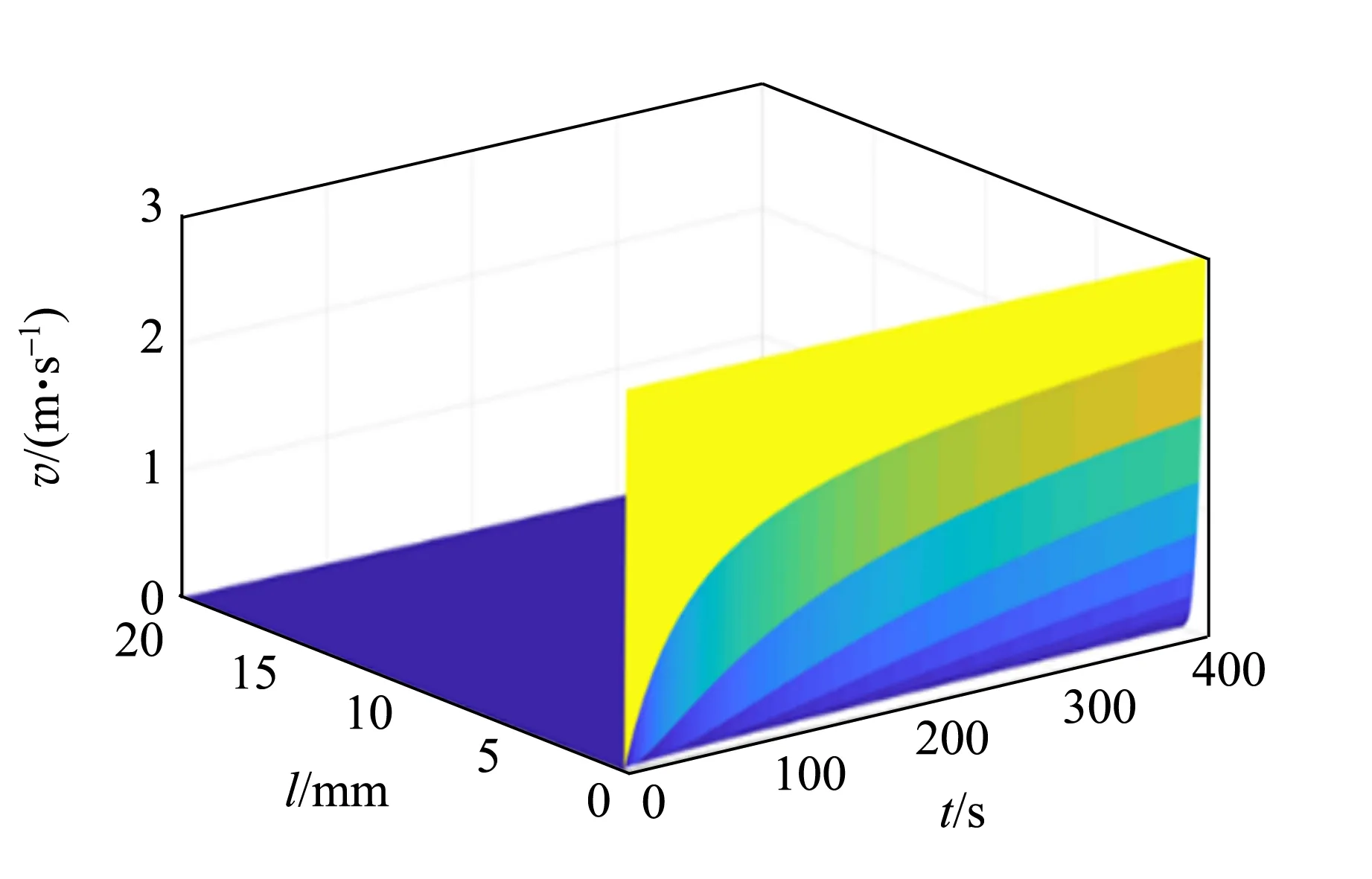
圖4 空氣速度場
1.4 數值模擬
設初始數組(ω,h)為(0,0),分別以0.1 r/s和0.01 m為步長增加(ω,h),求出每個數組對應的流速場,求出合力與合力矩,取合力與合力矩最接近0的數組,此時(ω,h)就是給定圓柱體的理想轉速和理想懸浮高度,如圖5所示. 初始條件:高3 cm,直徑12 cm,質量4.63 g,水柱初始高度設置為1.60 m. 數值模擬結果:理論轉速為5.33 r/s,理論懸浮高度為1.09 m.
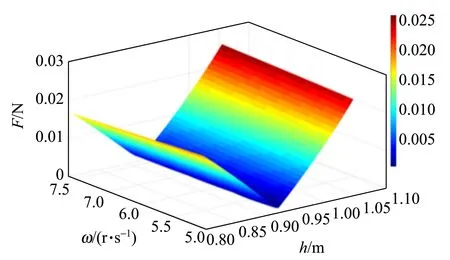
圖5 理論穩態轉速和懸浮高度
2 懸浮高度和轉速的測定
用Tracker軟件測量圓柱體穩態懸浮高度he和穩態轉速ωe,得到he,ωe與圓柱體直徑D和厚度l的關系,并與理論懸浮高度ht、理論穩態轉速ωt對比.
2.1 ω和l的關系
實驗測得ω與l如表1和圖6所示,ωt與l呈二次函數關系,二次項系數小于0,且ω″<0,實驗曲線與理論曲線吻合較好.
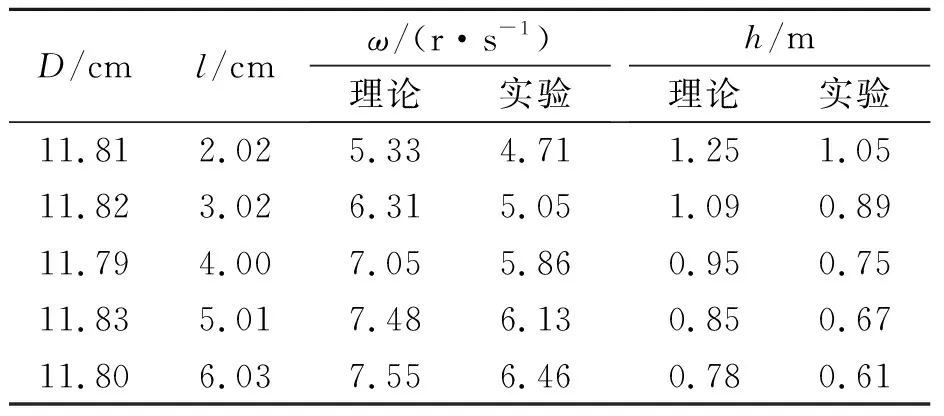
表1 ω,h與l的數據
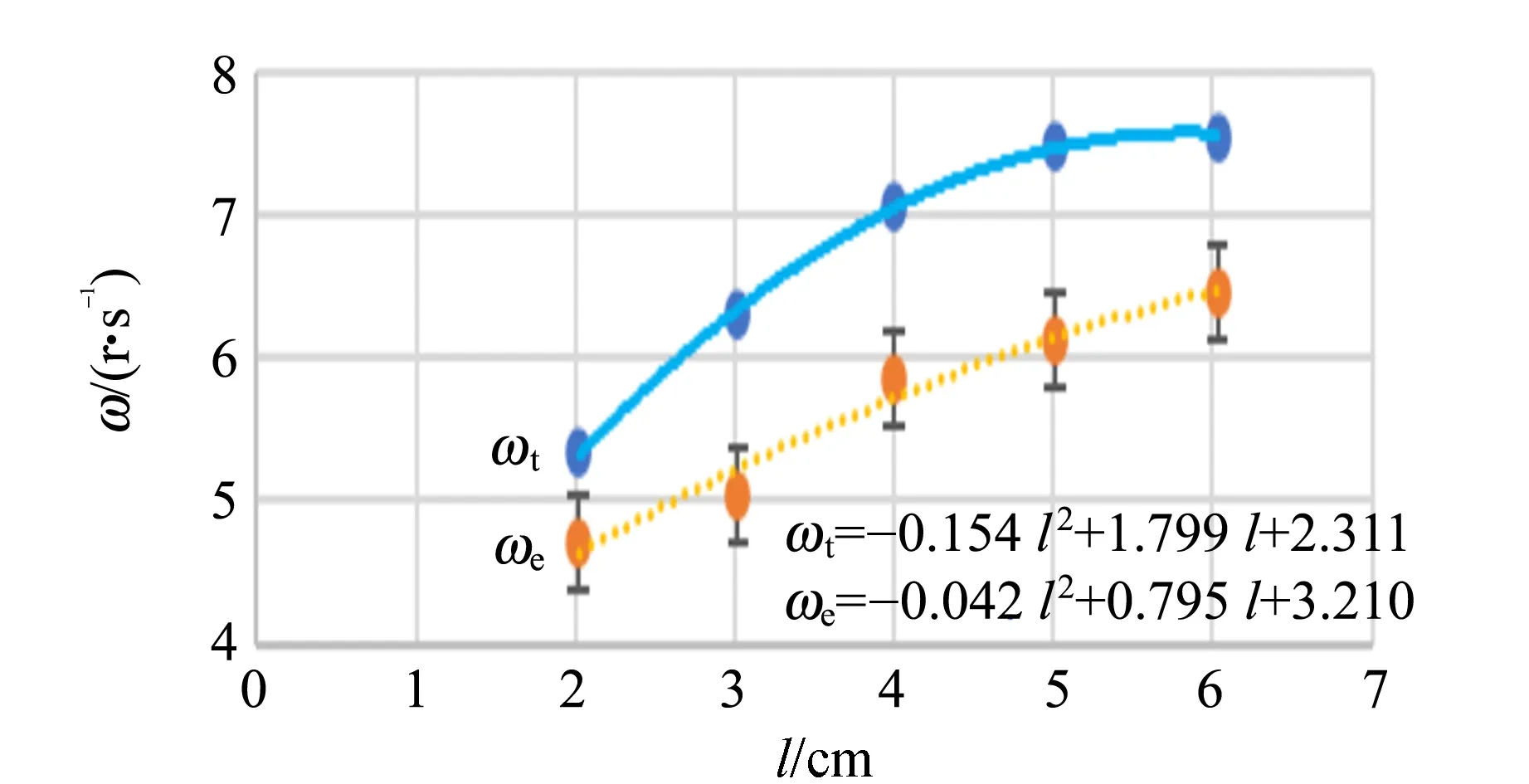
圖6 轉速ω和厚度l的關系
2.2 ω和D的關系
實驗測得ω和D如表2和圖7所示,ωt與D呈二次函數關系,二次項系數大于0,且ω″>0,實驗曲線與理論曲線吻合較好.
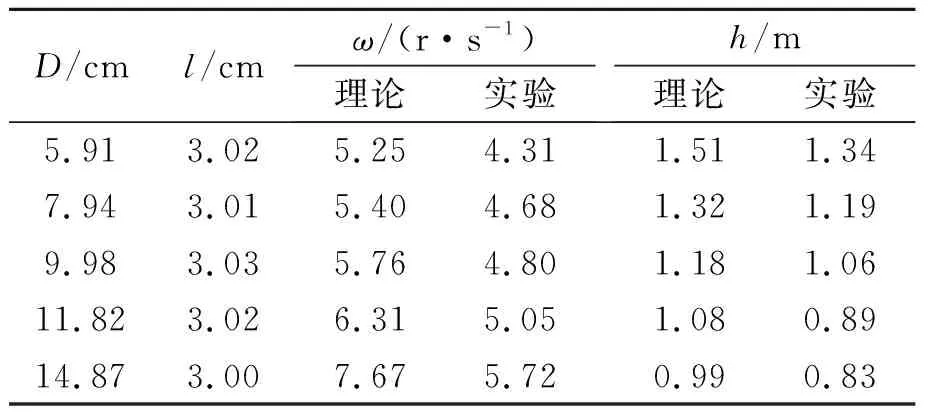
表2 ω和h與D數據
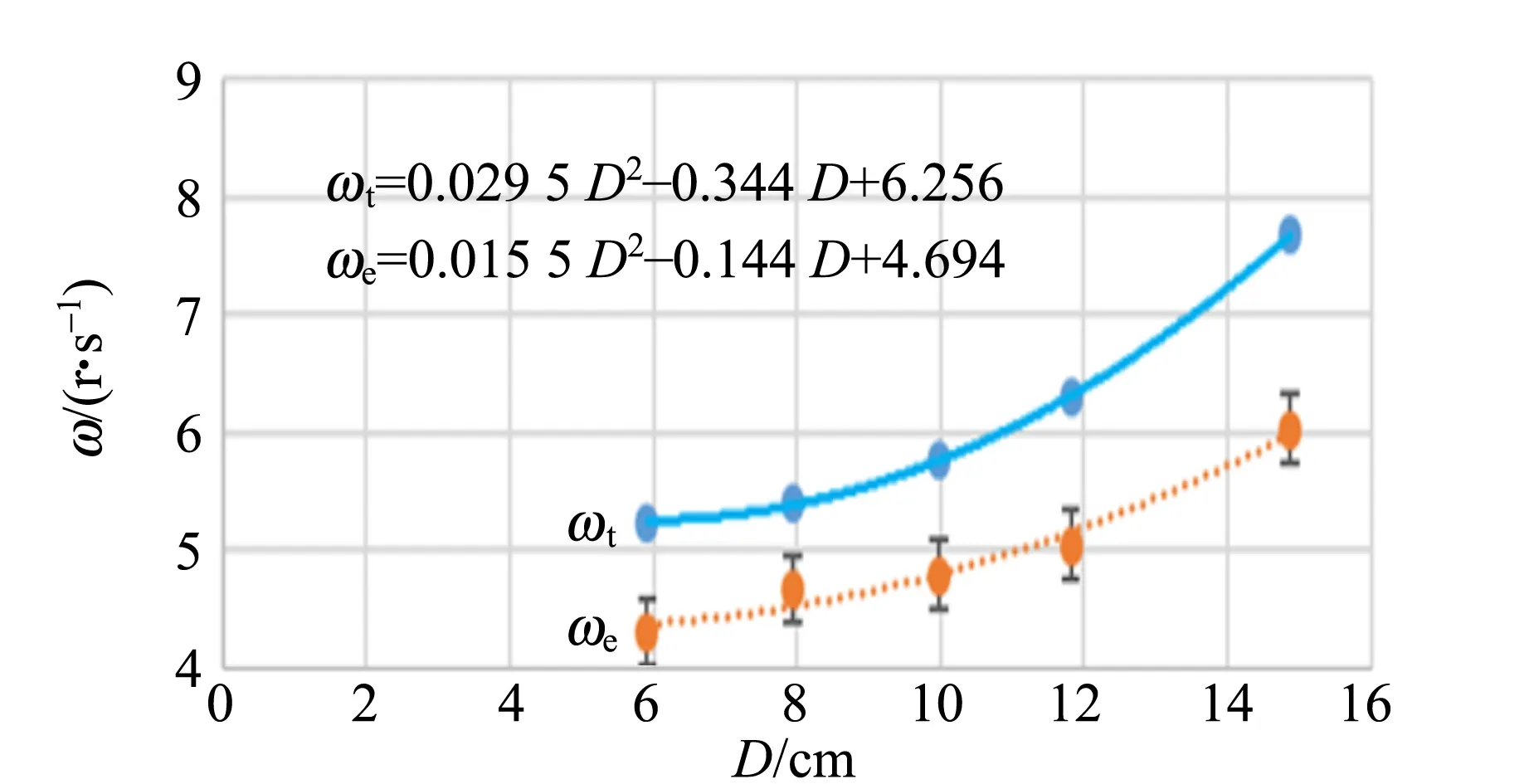
圖7 轉速ω和直徑D的關系
2.3 h和l的關系
實驗測得h與l如表1和圖8所示,ht與l呈二次函數關系,二次項系數大于0,且h″>0,實驗曲線與理論曲線吻合較好.
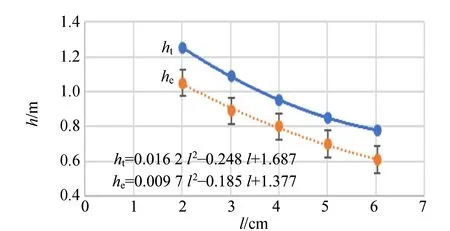
圖8 懸浮高度h和厚度l的關系
2.4 h和D的關系
實驗測得h和D如表2和圖9所示,實驗測量ht與D呈二次函數關系,二次項系數大于0,且h″>0,實驗曲線與理論曲線吻合較好.

圖9 懸浮高度h和直徑D的關系
3 流體懸浮的穩定性
3.1 穩定性的實驗探究
懸浮物體的穩定性和生態系統的抵抗力穩定性和恢復力穩定性特征十分契合,都與自身的結構特征和外界的干擾強度有關[7],所以引入生物學的概念,探究懸浮物的抵抗力和恢復力穩定性.
3.1.1 抵抗力穩定性
懸浮物體受到持續性擾動,強度不斷增大,將其能承受的最大擾動強度作為衡量抵抗力穩定性的標準. 水柱初始高度為h0,懸浮物體質量m,緩慢改變水柱與地面夾角θ,隨著水柱與豎直方向的夾角增大,擾動的強度也逐漸增大. 當水柱與豎直方向的夾角增大到一定值時,物體恰好到達平衡極限掉落,立刻停止改變水柱與豎直方向的夾角,測量射流出射點和落點的水平距離δx,δx與δθ關系為
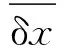
1)圓柱體
圖10是圓柱體從穩定懸浮到平衡極限過程. 實驗測量δx和l,如表3和圖11所示,圓柱體抵抗力穩定性在l=3.02 cm時最強.

(a)增大出射角 (b)臨界角 (c)掉落 圖10 改變出射角(圓柱體)

D/cml/cmδx/cmθs/(°)11.812.0243.312.511.813.0267.618.311.794.0049.515.411.835.0135.310.611.806.0327.39.4
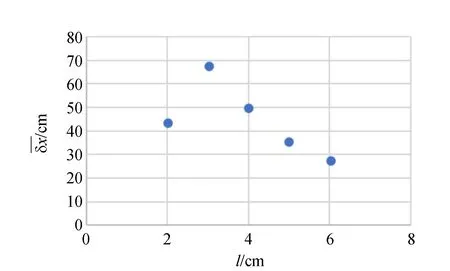
圖和l的關系
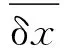

表和與D數據(圓柱體)
圖和D的關系(圓柱體)
2)球體

(a)增大出射角 (b)臨界角 (c)掉落圖13 改變出射角(球體)

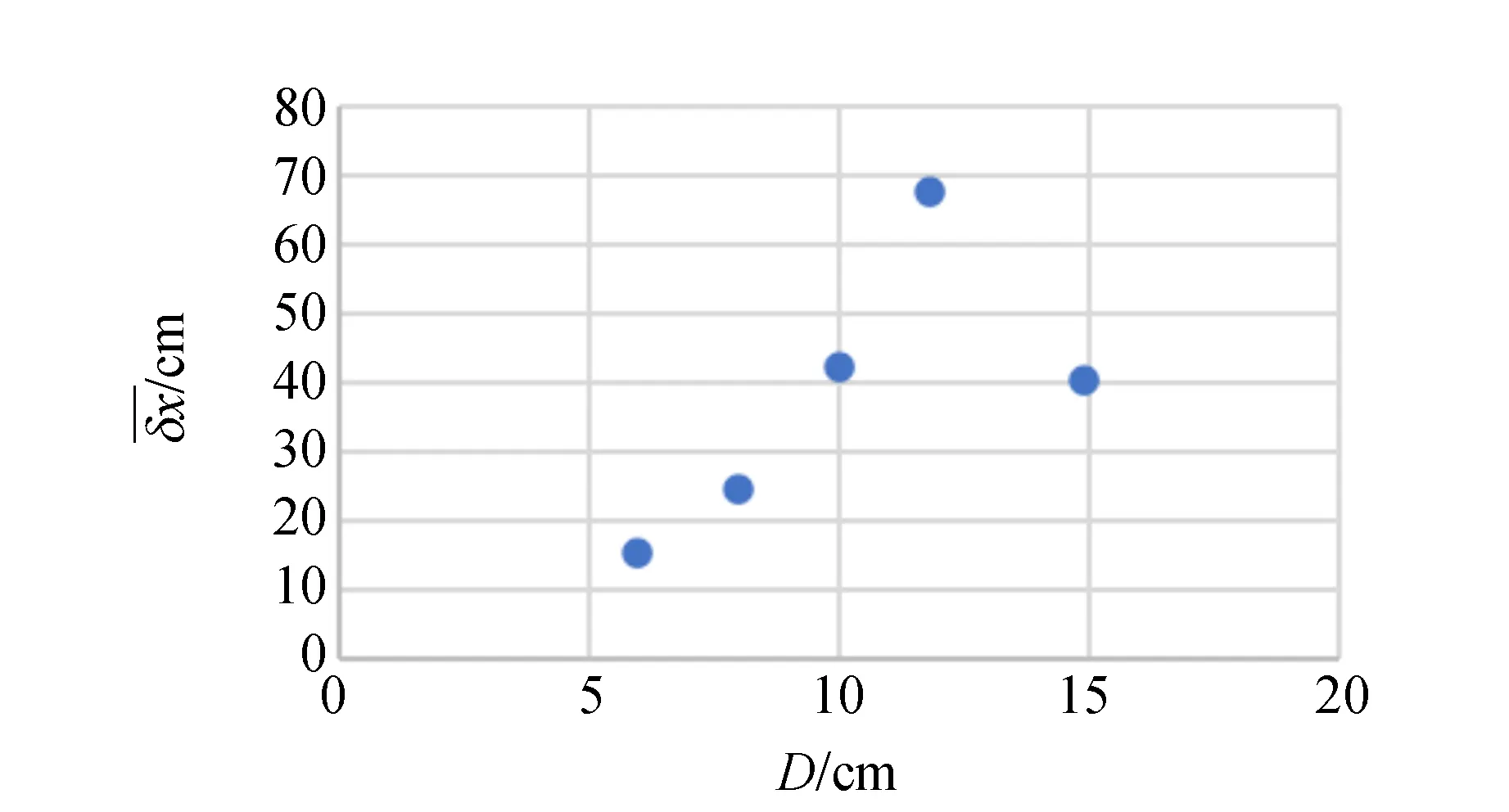
表和與D數據(球體)
圖和D的關系(球體)
3.1.2 恢復力穩定性
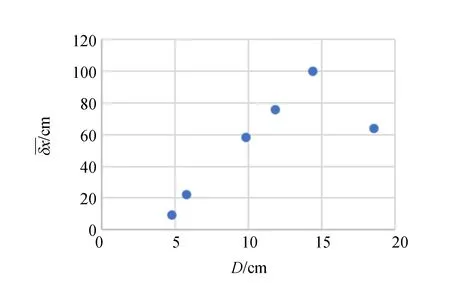
懸浮物經過瞬間擾動后,能重新回到懸浮狀態,稱其為恢復力穩定性. 將砝碼用輕質細線系在懸臂上,懸線長度L=1.000 m,懸線與豎直方向夾角為5°,靜止釋放砝碼撞擊懸浮物側面,若物體未掉落,則增大懸線與豎直方向的角度θs,步長5°,砝碼儲存的重力勢能轉化成的撞擊能量增大,當釋放角度增加到一定值時,物體被撞擊后無法恢復到平衡狀態,將此角度稱為臨界角度θl. 砝碼釋放角度與重力勢能Eg、撞擊能量Ek的關系(忽略空氣阻力影響)為
Eg=mgsinθs,Ek=ηEg,
其中η可近似認為是常數,其與碰撞過程中能量損耗有關.
Ek=ηmgsinθs,
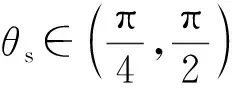
1)圓柱體
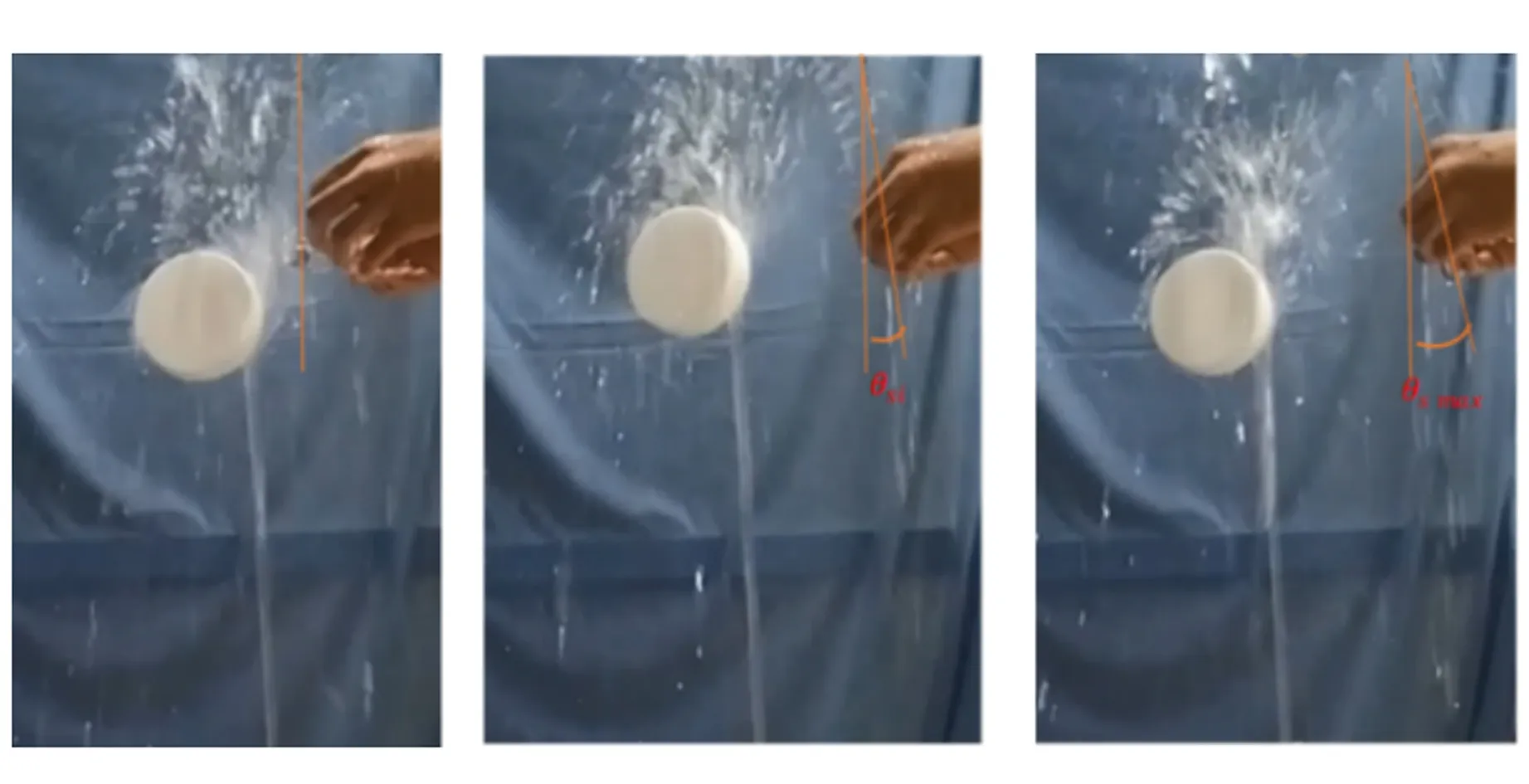
(a)靜止 (b)拉開砝碼 (c)臨界釋放角圖15 砝碼撞擊(圓柱體)
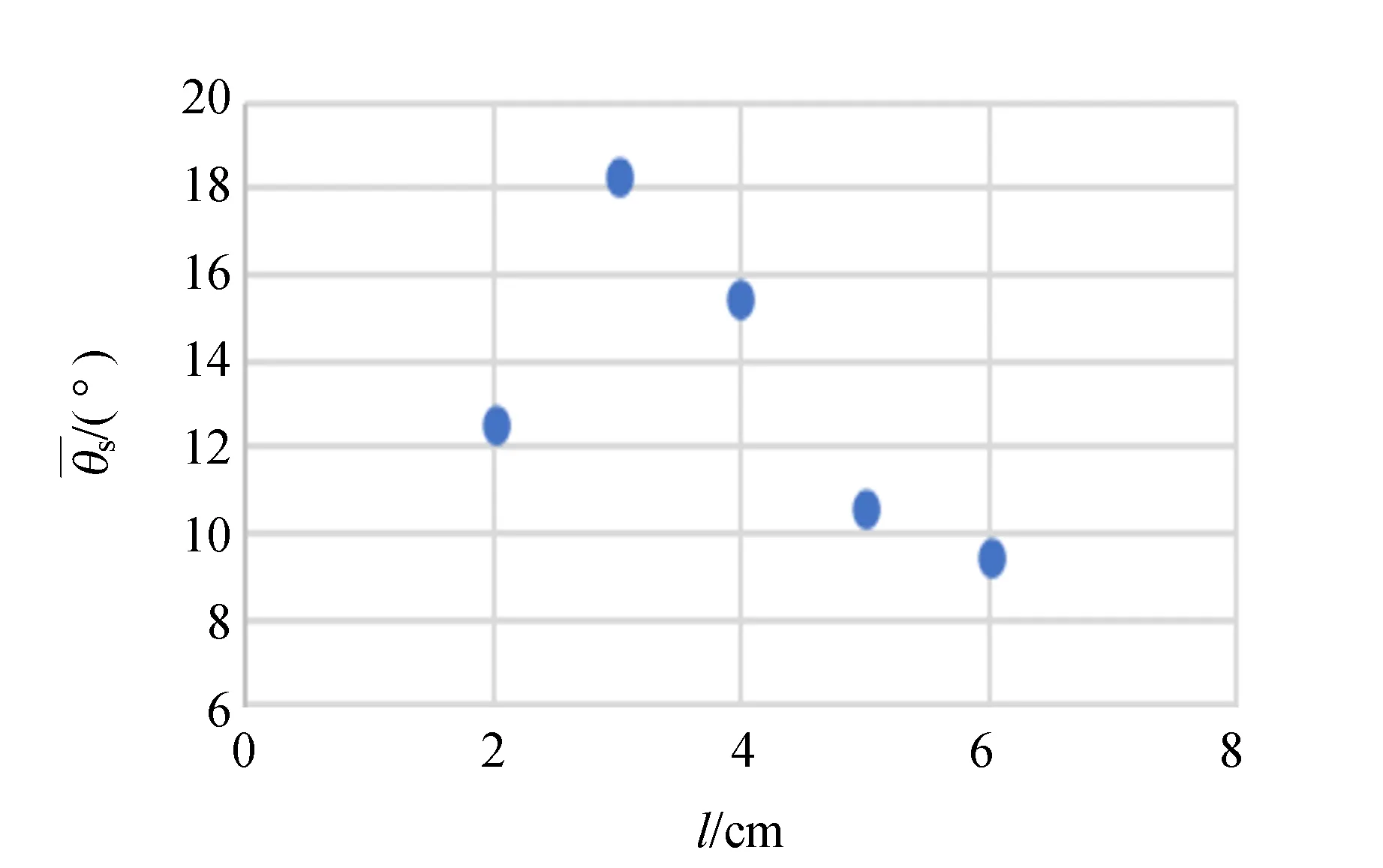
圖和l的關系


圖和D的關系(圓柱體)
2)球體

(a)靜止 (b)拉開砝碼 (c)臨界釋放角圖18 砝碼撞擊(球體)
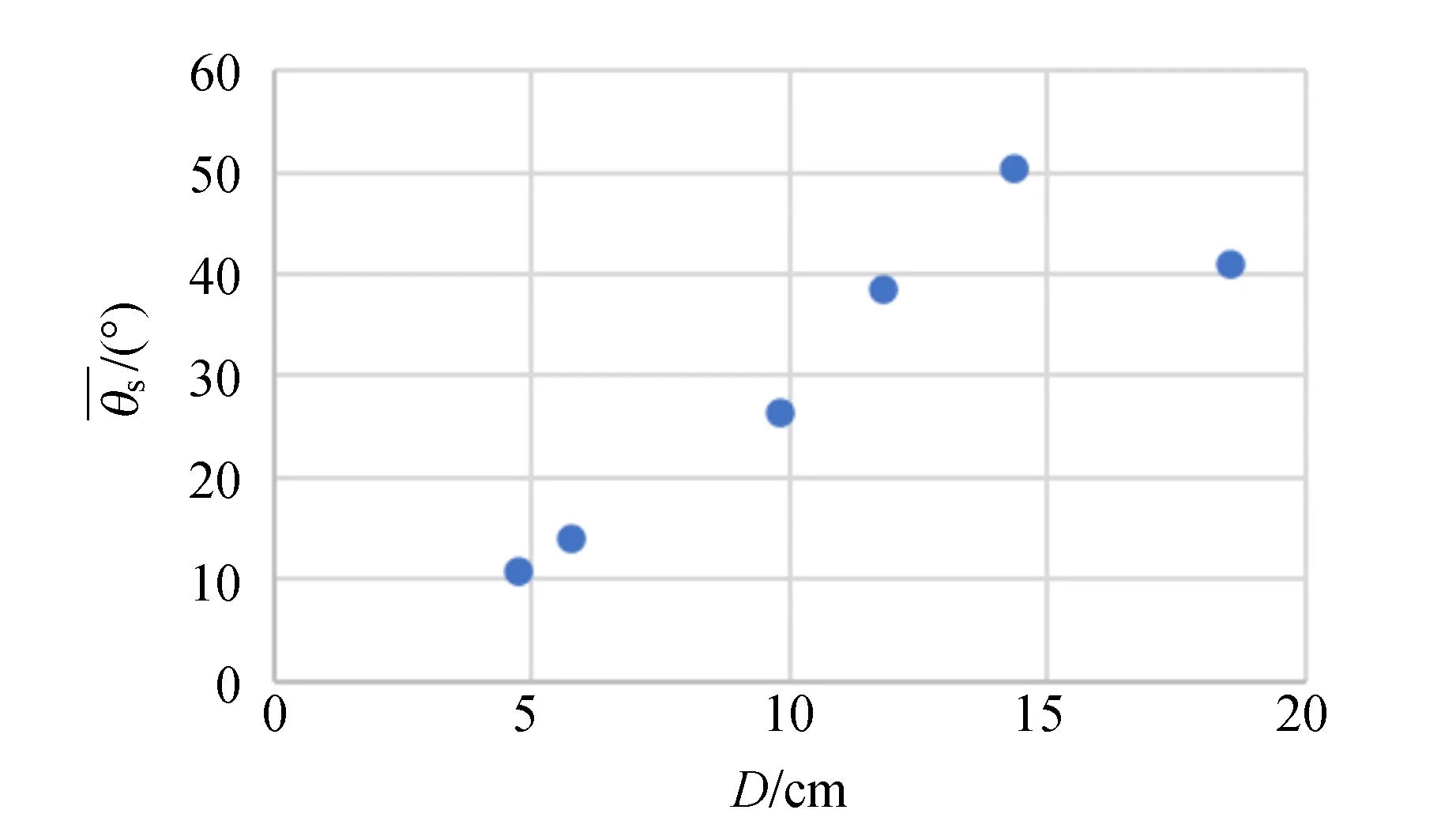
圖和D的關系(球體)
對比2種穩定性的實驗,發現球體和圓柱體的抵抗力穩定性和恢復力穩定性具有一致性,即抵抗力穩定性越強,恢復力穩定性也越強,則綜合穩定性越強.
3.2 穩定性的解釋
圓柱體和球體在受到擾動后,必然會發生豎直方向和水平方向的偏移,側面繞流產生的壓強變化會給圓柱體水平方向的回復力,水柱沖量的變化會給圓柱體豎直方向的回復力,
3.2.1 水平方向的回復力
伯努利方程適用于理想流體的穩定流動,當圓柱體最終處于穩定懸浮的狀態時,其側面的水流可以視為穩定流動:
(10)
式(10)中,C為常量,將圓柱體拿掉時水柱的最高高度為h0,則
C=ρgh0,
(11)
對于同一圓柱體,當其水平偏移量不同時,受到的水平回復力大小也不同,分為2類情況討論:
圖20表示水柱在不同時刻沖擊圓柱體的點不同,導致在圓柱體側表面形成不同的繞流,(a)和(b)情況都不是穩定情形,由式(10)和(11)得:
(12)
(13)

(a)向左 (b)向右圖20 水平回復力
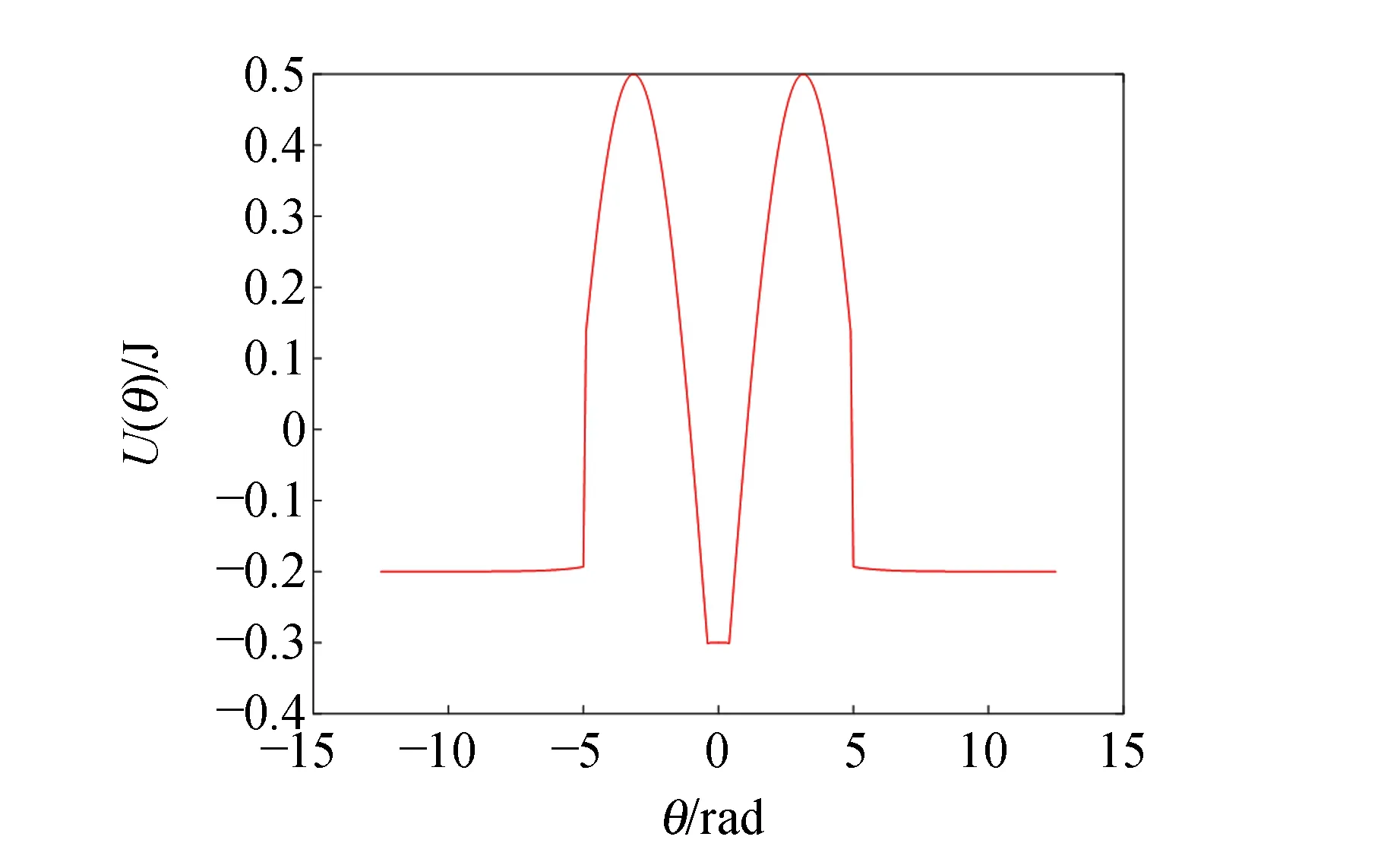
水柱到達A點和B點的能量損耗主要包括重力勢能損耗、黏滯阻力損耗和轉化為沖擊力的損耗,重力勢能損耗相同,黏滯阻力和轉化沖擊力損耗且都是點A大于點B,所以剩余動能EkA pA>pB. (14) 考慮圓柱體側面的總體壓強分布結合大氣壓,最終得到壓強梯度力方向向右,為 dFA=[p0-(p0-pA)]dS, dFB=[p0-(p0-pB)]dS, 其中,FA為圖20(a)情況由壓強分布產生的水平回復力 FB為圖20(b)情況由壓強分布產生的水平回復力 結合式(14)得到: FA (15) FA和FB方向向右,形象地說,在一定范圍內,偏心角越大,圓柱體受到被水柱吸附的力越大. 再考慮沖擊力沿水平方向的分力,由式(4),得到沖擊力F1的表達式,此時偏心角θ是時變的: 沖擊力沿水平方向的分力F1x為 再考慮圖20中2種情況,FAx為圖20(a)情況下沖擊力沿水平方向的分力(起到的作用與回復力相反): FBx為圖20(b)情況下沖擊力沿水平方向的分力: FAx>FBx, (17) 結合式(15)和式(16)得到 FAxback=FA-FAx<0 (16) 圖20(a)中偏心角較大,圓柱體受到的水平回復力向左,圖20(b)圓柱體受到向右的水平回復力,由零點存在定理,一定存在讓圓柱體剛好達到平衡的點,不受回復力,即?θ∈(θA,θB),使 F(θ)xback=0. 3.2.2 豎直方向的回復力 由式(4)得到沖擊力F1沿豎直方向的分力 h表示實時的懸浮高度,是時變量.FAy為圖21(a)情況下沖擊力沿豎直方向的分力: FBy為圖21(b)情況下沖擊力沿豎直方向的分力 顯然FAy FAyback=FAy-G<0; 圖21(b)中豎直回復力為FByback,方向向上: FByback=FBy-G>0, 由零點存在定理,一定存在使圓柱體剛好達到平衡的點,不受回復力,即?h∈(hA,hB),使 F(h)yback=0. (a)向下 (b)向上圖21 豎直回復力 3.2.3 勢能最低點 勢能最低點(θ,h),其物理含義是圓柱體受到擾動后所趨向的點. 數值模擬使用迭代試探的方法,得到圓柱體穩定時的懸浮高度和轉速. 對于受到擾動后的圓柱體,其周身水流速度場是時變的,所以無法求出勢能最低點的具體位置. 但是不影響理論上存在勢能最低點,此點的存在對圓柱體受到擾動后能回歸穩定點提供了合理解釋. 如圖22所示,對于抵抗力穩定性和恢復力穩定性的一致性,也可以從勢能的角度解釋,由于勢能最低點(θ,h)的存在,并且勢能曲線是連續的,導致勢能曲線存在低谷區,谷的深度與勢能最小值U(θ,h)負相關,懸浮時的勢能最小值越小,谷越深. 物體掉落后,其勢能為外部環境的勢能,即從峰頂掉落到外側的平直的勢能曲線上. 圖22 勢能曲線圖(定性) 為了理解方便,可以類比谷底有一小球,抵抗力穩定性的實驗是不斷增大射流偏轉角,等同于勢能最低點不斷變大,即谷底緩慢抬升,如圖23所示,當谷底上升到超過峰頂后,懸浮物掉落到外界環境中. 圖23 勢能最低點的抬升 恢復力穩定性實驗是對小球進行撞擊,而整個懸浮系統是不變的,所以谷底的深度不變,而是把小球緩慢地從谷底拉到峰頂,小球到達封頂后,即懸浮物掉落到外界環境中. 所以谷底的初始深度越深,懸浮物的抵抗力穩定性和恢復力穩定性都越大,論證了抵抗力穩定性和恢復力穩定性具有一致性. 定解了圓柱體繞流的流速場,求出圓柱體的理論懸浮高度和理論轉速,實驗與理論符合程度良好. 探討了懸浮物體的穩定性,研究了影響球體和圓柱體穩定性的因素,實驗結果表明:轉速與厚度l、直徑D呈正相關,懸浮高度與厚度l、直徑D呈負相關,對于泡沫材質的圓柱體,抵抗力和恢復力穩定性具有一致性,其在l=3.02 cm,D=11.81cm時穩定性最強.對于泡沫材質的球體,抵抗力和恢復力穩定性也具有一致性,在D=14.37 cm時最強,直徑相同的球體比圓柱體恢復力穩定性強.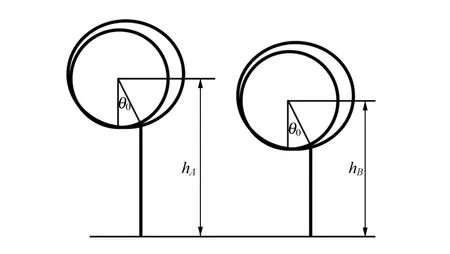

4 結 論

