濕蒸汽激勵下圍帶碰撞-摩擦阻尼計算方法

聶凡茹，唐委校

(1.山東大學機械工程學院，山東 濟南 250061) (2.高效潔凈機械制造教育部重點實驗室(山東大學)，山東 濟南 250061) (3.機械工程國家級實驗教學示范中心(山東大學)，山東 濟南 250061)

具有復雜結構特點(長軸系、大柔性葉片和Z形圍帶等)的大型汽輪機轉子系統在轉速和濕蒸汽激勵下會被誘發強非線性振動，直接影響整個汽輪機組的運行安全。目前工程上廣泛采用圍帶來抑制轉子系統振動響應和消耗振動能量。很多學者對裝備圍帶的轉子系統進行了動力學特性研究：蔣愛華[1]建立了基于Hertz接觸理論的彈簧阻尼圍帶碰撞模型，數值分析了初始間隙和轉速對轉子系統主共振響應的影響規律；能海強[2]考慮摩擦系數、接觸剛度、初始間隙、接觸角及轉速的影響，建立了彈簧碰撞-Sgn摩擦的平行四邊形圍帶碰撞-摩擦模型，數值分析了升降速工況下接觸角和初始間隙對轉子系統響應特性的影響規律；何冰冰等[3]基于離心剛化效應建立了非線性彈簧-指數衰減Sgn平行四邊形圍帶碰撞-摩擦模型，數值分析了非線性剛度比和初始間隙對振動位移響應的影響規律。劉錦[4]基于遲滯摩擦模型提出轉速激勵下平行四邊形圍帶摩擦阻尼的計算方法，定量分析了接觸角、初始間隙、摩擦系數和接觸剛度對圍帶摩擦阻尼和系統振動特性的影響規律。郭冰[5]基于遲滯摩擦模型提出轉速和濕蒸汽多頻激勵下平行四邊形圍帶摩擦阻尼的計算方法，數值分析了不同流量下進氣參數和不同轉速對系統振動響應的影響規律。

針對現有Z形圍帶阻尼模型未能考慮圍帶間相對滑動速度影響，計算方法無法定量計算出考慮圍帶間相對滑動速度影響的Z形圍帶碰撞-摩擦阻尼等問題，本文以大型汽輪機Z形圍帶為例，建立在轉速和濕蒸汽激勵下考慮圍帶間相對滑動速度影響的Z形圍帶彈簧碰撞-指數衰減遲滯摩擦模型，提出一種圍帶碰撞-摩擦阻尼計算方法，定量計算圍帶阻尼對轉子系統振動特性的影響。

1 Z形圍帶碰撞-摩擦阻尼模型及其計算公式

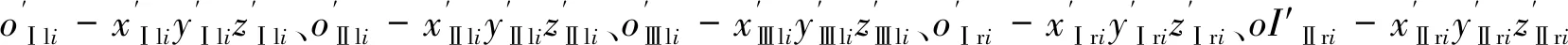
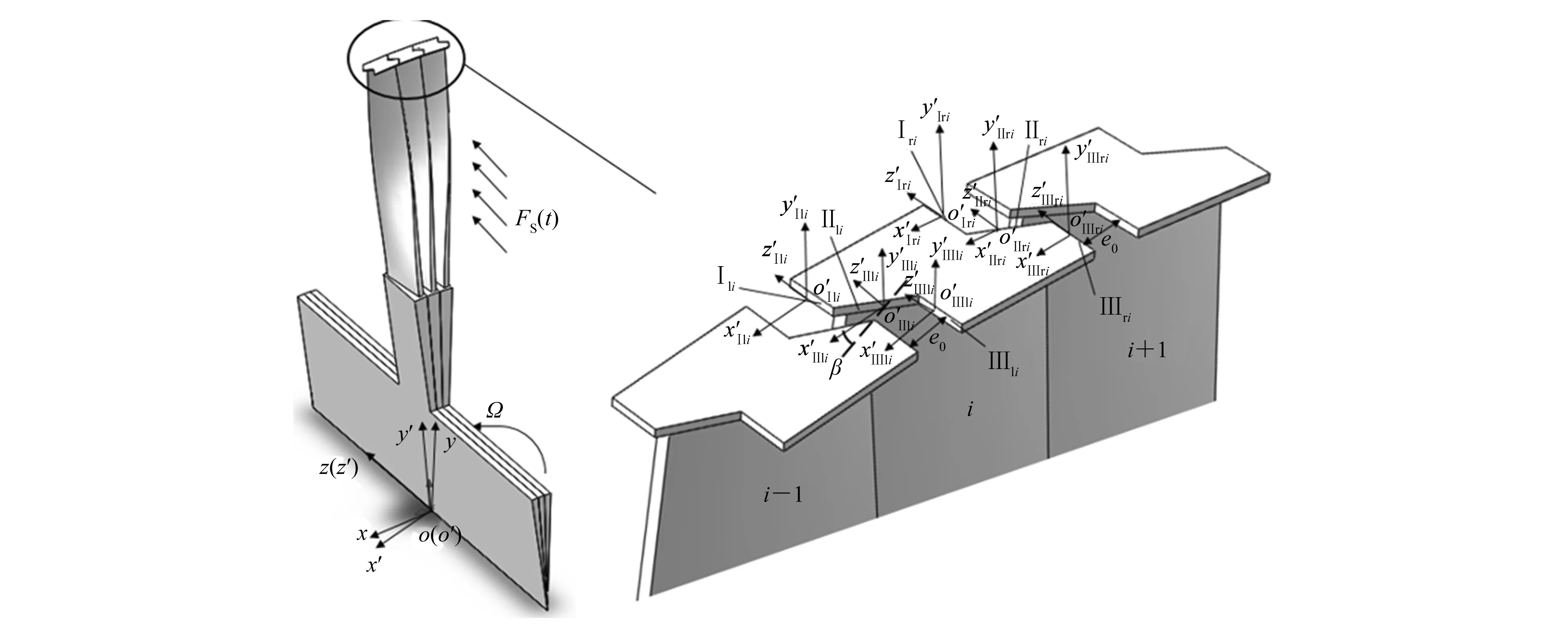
圖1 末級轉子的Z形圍帶

1.1 轉速和濕蒸汽激勵下圍帶碰撞-摩擦阻尼模型

采用快速傅里葉變換(fast Fourier transform，FFT)可將包含轉速等效離心激勵FΩ(t)和濕蒸汽激勵FB(t)的外部激勵FS(t)表示為若干個諧波激勵分量的疊加[5]，即：

(1)

式中：Fa(y′)為第a階諧波激勵分量的幅值；ωa和φa為激勵分量的頻率和相位角；t為時間；D為諧波激勵最大階數。

基于Rhee等[6]的假設，按時間順序將圍帶間運動簡化為如下循環運動過程：碰撞—黏滯—滑動摩擦—黏滯—分離—再碰撞。區別于平行四邊形圍帶，Z形圍帶在一個運動周期的不同時間段內有不同的接觸面間發生接觸運動。本文用彈簧模型[2]來描述相鄰圍帶間的法向碰撞力fim(t)，用指數衰減[7]遲滯摩擦模型描述相鄰圍帶間的切向摩擦力fif(t)，建立彈簧碰撞-指數衰減遲滯摩擦模型來描述Z形圍帶間運動。

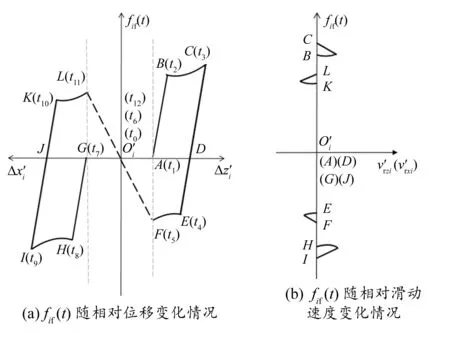
圖2 fif(t)變化回線

t6至t7，Ⅱli面與Ⅱr(i-1)面間相對法向位移從0逐漸增大，增大到e0tanβ時(即t7時刻)相鄰圍帶開始接觸，t7時刻圍帶接觸面間無作用力；t7至t11，這對接觸面切向經歷“黏滯—相對滑動—黏滯—反向相對滑動”運動過程；從t11開始，相鄰圍帶分離，fif(t)和fim(t)突降為0。隨著葉片振動，相鄰圍帶再開始新一輪循環運動過程。上述一個循環周期“t0—t6—t12”中，fif(t)和fim(t)可表示為：

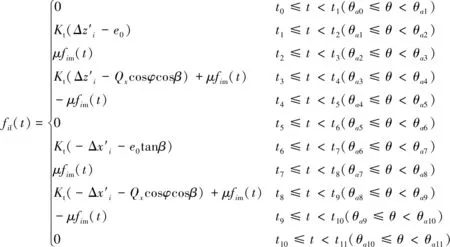
(2)

(3)

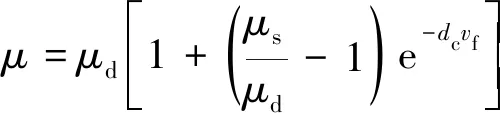
(4)

式中：Kt和Kn分別為圍帶接觸面的切向接觸剛度和法向接觸剛度；μ為指數衰減模型中的摩擦系數[7]；vr為圍帶間相對滑動速度；μd為動摩擦系數；μs為靜摩擦系數；dc為衰減系數；φ為轉子轉角，φ=Ωt；Qx和Qz為o-xyz下Z形葉片圍帶振動位移分量；t0～t11為各個狀態的轉換時刻點；θai為各個時刻點對應的振動相位角。

θa0=-π/2

θa1=arccos[e0/R(t1)]

θa2=arccos{[e0/R(t1)]+μ[KnR(t4)tanβ+KnQzsinβ-Kne0]/[KtR(t2)]}

θa3=0

θa4=arccos{1-2μ[KnR(t4)tanβ+

KnQzsinβ-Kne0]/[(Kt+2μKntanβ)R(t4)]}

θa5=-θ1

θa6=π/2

θa7=arccos[e0tanβ/R(t7)]

θa8=arccos{[e0tanβ/R(t7)]+μ[KnR(t10)-KnQzcosβ-Kne0tanβ]/[KtR(t8)]}

`θa9=π

θa10=arccos{1-2μ[KnR(t10)-KnQzcosβ-Kne0tanβ]/[(Kt+2μKn)R(t10)]}

θa11=2π-θ7

θa12=3π/2

式中：R(t)=Qxcosφcosβ。

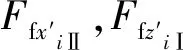
(5)

(6)

(7)

(8)

式中：

綜上可知，已知Z形圍帶接觸面間切向力和法向力的各段起止時間及Z形圍帶的瞬時振動響應位移即可求得Z形圍帶碰撞-摩擦阻尼，但只通過式(1)～(8)無法對其求解，因此本文提出一種圍帶碰撞-摩擦阻尼的計算方法。

1.2 圍帶碰撞-摩擦阻尼計算公式及方法

轉子系統的質量矩陣Ms、剛度矩陣Ks、轉子系統圍帶碰撞-摩擦等效剛度矩陣Mfm、等效阻尼矩陣Cfm和轉子系統位移矢量Q(t+τ)關系為：

(9)

(10)

(11)

(12)

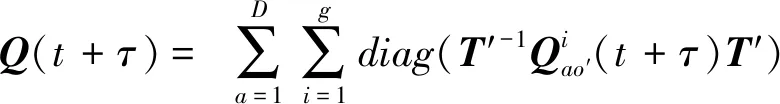
(13)

其中：

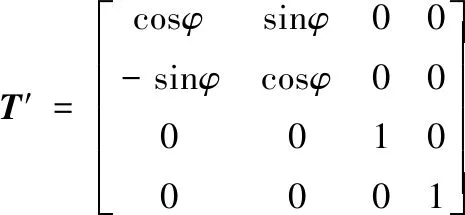
(14)

式中：g為系統葉片數；Msi，Ksi，Kifm和Cifm為第i個帶圍帶葉片及其對應角度下輪轂及軸的質量矩陣、靜剛度矩陣、圍帶碰撞-摩擦等效剛度矩陣和圍帶碰撞-摩擦等效阻尼矩陣；τ為遲滯時間；T′為o′-x′y′z′與o-xyz的變換矩陣。

考慮圍帶碰撞-摩擦阻尼的轉子系統振動微分方程為：

(15)

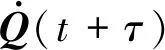
轉子系統臨界阻尼ccri的表達式為：

ccri=2msωnfm

(16)

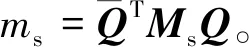
(17)

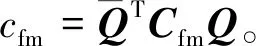
(18)

式中：Ast/Ast+T為系統振幅比，Ast和Ast+T分別為t時刻和(t+T)時刻系統在不同工況激勵下振動位移響應幅值；T為系統振動周期。則轉速和濕蒸汽激勵下圍帶碰撞-摩擦阻尼cfm為[4]:

(19)

由式(18)和式(19)可知，為了求解圍帶碰撞-摩擦阻尼，需要利用模態分析確定系統模態質量和固有頻率；需要利用瞬態響應分析得到系統在不同工況激勵下振動位移響應幅值。據此，本文建立轉速和濕蒸汽激勵下圍帶碰撞-摩擦阻尼計算方法，具體步驟如下：

1)用三維建模軟件建立相鄰Z形圍帶間法向初始間隙為e0、接觸角為β的轉子系統三維幾何模型，然后導入ANSYS中進行離散，得到有限元模型；

2)用ANSYS模態分析模塊對有限元模型施加轉速，得到系統模態質量ms和固有頻率ωnfm；

3)用ANSYS建立并離散包含靜葉和動葉的流體計算域，導入CFX中，進行流場仿真得到壓力分布載荷，用FFT變換得到濕蒸汽激勵FB(t)；

4)用ANSYS Explicit Dynamics 模塊對有限元模型做前處理，設置接觸條件中的摩擦系數μd及μs、衰減系數dc和接觸剛度Kt及Kn，施加Ω和FB(t)，調用ANSYS LS-DYNA求解器LS-PrePost做后處理，得到系統最大振動位移響應曲線，代入式(18)和式(19)計算可得Cfm。

2 實例計算分析

以某1 000 MW大型汽輪機低壓末級轉子系統為例，Z形圍帶參數為β=30°，e0=0.5 mm，μs=0.05，Kn=0.2，葉片長度L=1 400 mm，采用軸向對稱性、相對柔度法和CN群論法縮減轉子系統至包含3個帶Z形圍帶的葉片及其對應角度下輪轂和軸的基本扇區，采用本文提出的圍帶碰撞-摩擦阻尼計算方法定量計算圍帶碰撞-摩擦阻尼及其對轉子系統振動特性的影響，并用本文提出的圍帶阻尼計算方法計算得到的文獻[8]中實驗葉片組的振動響應振幅比與文獻實驗數據進行對比。

2.1 Z形圍帶碰撞-摩擦阻尼及其對系統振動特性影響

采用本文提出的圍帶阻尼計算方法中步驟1)和步驟2)對轉速Ω=1 500 r/min下的轉子系統進行模態分析，得到表1中系統前5階的固有頻率。

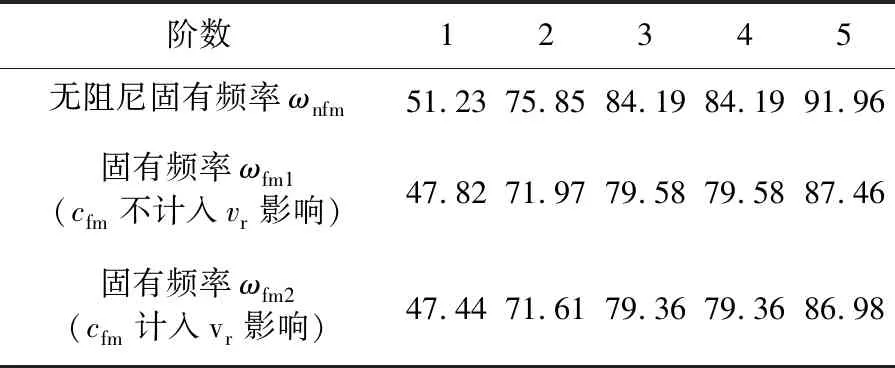
表1 轉子系統的前5階固有頻率 單位:Hz

由表可知，Z形圍帶碰撞-摩擦阻尼使系統第一、二階固有頻率均遠離轉速激勵倍頻，影響較大，且忽略vr影響的cfm1比考慮vr影響的cfm2對系統固有頻率的降低效果差但差別不大。

采用圍帶阻尼計算方法中步驟3) 和步驟4)對額定流量工況下的轉子系統進行瞬態響應分析，得到系統振動響應位移曲線及振幅比，計算得到的cfm列于表2。

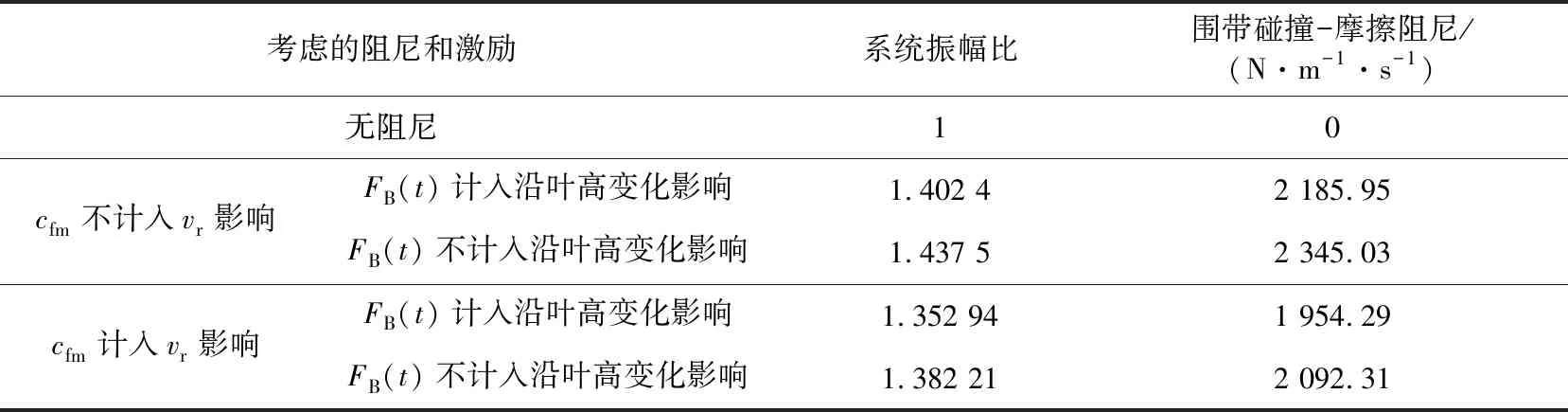
表2 轉子系統的圍帶碰撞-摩擦阻尼

由表可知，Z形圍帶碰撞-摩擦阻尼降低了系統振動位移響應幅值，影響較大，考慮vr對cfm的影響和FB(t)幅值變化的圍帶接觸模型的cfm比不考慮上述影響的cfm對系統振動響應特性影響小。

2.2 阻尼模型及計算方法的驗證

本文采用圍帶阻尼計算方法對文獻[8]中不同初始間隙e0下帶Z形圍帶的實驗葉片組建模，施加實驗激勵進行瞬態響應分析得到振動位移響應，所得振幅比與文獻[7]實驗數據中的響應振幅比的誤差見表3。

由表可知，兩者誤差小于13%，證明本文提出的Z形圍帶碰撞-摩擦阻尼模型及其計算方法是可行的。分析可知，小初始間隙區間的轉子系統圍帶碰撞-摩擦阻尼較大，圍帶碰撞摩擦運動減振效果也較好，且Z形圍帶碰撞-摩擦阻尼隨著初始間隙的增加呈現出先降低再升高后降低的變化趨勢。

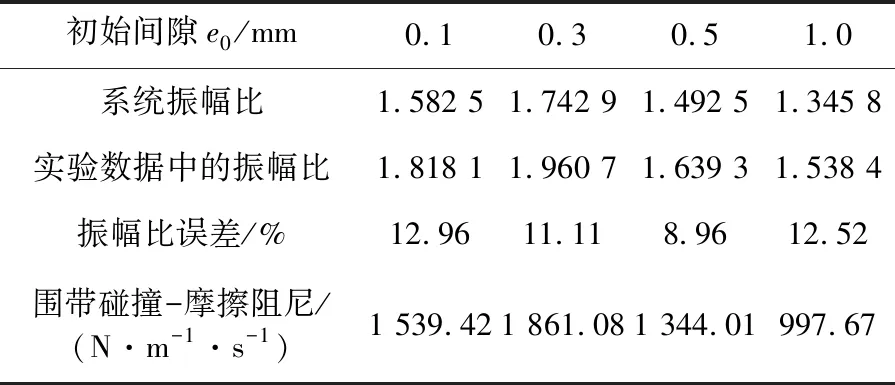
表3 計算得到不同e0下文獻[8]中帶Z形圍帶的

3 結論

針對大型汽輪機末級轉子系統Z形圍帶阻尼模型未能考慮圍帶間相對滑動速度影響、現有計算方法無法定量得到考慮圍帶間相對滑動速度影響的Z形圍帶碰撞-摩擦阻尼等問題，本文建立了在轉速和濕蒸汽激勵下考慮圍帶間相對滑動速度影響的Z形圍帶彈簧碰撞-指數衰減遲滯摩擦模型，并提出一種Z形圍帶碰撞-摩擦阻尼計算方法，由計算結果可得如下結論：

1)Z形圍帶碰撞-摩擦阻尼降低了轉子系統的固有頻率和振動位移響應幅值，對系統振動特性的影響不可忽略；

2)Z形圍帶碰撞-摩擦阻尼中的圍帶間相對滑動速度因素對系統固有頻率的降低效果影響不大，考慮圍帶間相對滑動速度和濕蒸汽激勵幅值沿葉高變化的Z形圍帶碰撞-摩擦阻尼比不考慮上述影響的圍帶阻尼對系統振動響應特性影響小；

3)Z形圍帶碰撞-摩擦阻尼隨著初始間隙的增加呈現出先降低再升高后降低的變化趨勢，將采用此計算方法得到的文獻中帶Z形圍帶葉片組的振動響應幅值比與文獻實驗數據進行對比，誤差小于13%，驗證了本文提出的阻尼模型及計算方法，為工程通過調節影響參數抑制轉子振動提供了理論依據和實施方法。