應急裝備制造網絡的動態資源配置

裴 植 戴 旭 袁依輪 易文超 陳 勇

浙江工業大學機械工程學院，杭州，310023

0 引言

裝備制造業的發展水平是國家制造能力和科技實力的體現，在當前生產網絡化大背景下已形成了以核心制造企業為主導，協同上下游企業和其他服務外包企業的網絡結構[1]。面對突發公共衛生事件，管理部門及相關企業需要快速響應，包括及時分配應急裝備物資、合理制定生產計劃來控制傳染病擴散[2]，關鍵的應急物資包括呼吸機、防護服等醫療裝備以及余氯快速測定儀等監測裝備。在裝備生產過程中,系統狀態、質量和關聯關系存在隨機性，制造服務信息具有時變性[3]。應急裝備的制造需求呈現出實時性強和波動性高的特征，從而實時影響著所對應任務之間的功能需求和流程需求[4]，使得動態資源的有效配置成為應急裝備制造服務網絡中亟需解決的問題之一。

為提高制造企業的競爭力，孫林巖等[5]提出融合制造與服務的服務型制造(service-oriented manufacturing, SOM)新模式，其整合、增值和創新等特點可促進制造業結構升級和區域經濟的均衡發展。近十余年來，服務型制造作為一種新型制造模式越來越受到國內外企業界和學術界的重視[6]，制造型服務商和服務型制造商組成的服務型制造網絡可整合資源、協同制造以及共享利益。服務型制造企業為簡化生產環節以增強企業競爭力，會模塊化分解生產工序，并將非核心制造業務外包給網絡中其他節點企業，或在市場直接采購原材料或半成品[7]。基于服務型制造網絡云結構，單子丹等[8]構建了服務型制造網絡流程的優化模型，其研究結果表明，客戶需求的不確定性會影響服務型制造網絡(service-oriented manufacturing network, SOMN)的制造流程。

原毅軍等[9]指出，裝備制造業的網絡結構中存在耦合關系，不同企業在制造網絡中需要共享信息、相互協調，為核心制造企業提供支持。為定量化解決不確定需求下的應急裝備制造網絡節點設計問題，向峰等[10]制定了服務水平等級協議以對制造服務能效進行評估。在應急裝備生產過程中，生產數據信息具有隨加工過程的時變特性，這對跨企業間的數據、信息和知識的協同與交互效能提出了更高的要求，針對此，WU[11]將排隊網絡模型應用于制造服務網絡的性能分析。針對由制造集成商、服務承包商與需求市場組成的產品服務供應鏈，彭永濤等[12]借助變分不等式探討各節點的最優決策與均衡條件，分析產品服務關聯度、客戶異質性偏好和服務水平對供應鏈網絡中自營和外包服務流的影響。針對具有排隊現象的服務型供應鏈，SCHONLEIN等[13]利用近似流體排隊模型分析了網絡結構的穩定性。在制造車間層級，NEGRI等[14]基于開環排隊網絡和近似參數分解算法權衡生產資源投資成本和在制品的庫存成本，可有效求解作業網絡的資源分配。考慮供應鏈網絡中商品的變質具有不確定性，HANUKOV等[15]利用排隊模型減少產品在配送中心的駐留時間，并構建了針對運營成本與碳排放的多目標魯棒優化模型。由于應急裝備訂單的到達具有高度動態性和不確定性，故本文假設制造服務網絡的產品流具有時變函數形式，KIM等[16]的研究曾證明該函數形式的到達過程符合非齊次泊松過程(NHPP)的性質。

應急裝備制造服務網絡的節點設計包括設施布局、資源配置以及資源調度等問題。為解決裝備制造服務中的資源建模、資源需求、資源搜索、資源匹配和資源響應等問題，沈磊等[17]建立了面向裝備制造行業的云制造服務需求與資源響應模型，并采用直覺梯形模糊集匹配算法進行求解。針對應急裝備的制造網絡設計需要同時考慮需求的不確定性和時效性，制造等待時間過長將會導致客戶撤銷訂單，故應急裝備制造具有產品交貨期短、生產加工和運輸時間短等苛刻的服務要求。針對有高時效性要求的制造服務網絡，ASKIN等[18]結合時變的制造需求分析系統的性能指標，通過仿真方法驗證近似算法的有效性。

現有文獻鮮有涉及在外部需求符合NHPP時，考慮帶有系統性能約束的制造服務網絡資源配置優化問題。為此，筆者首先建立一個三層級制造服務網絡，據此構建四個節點的排隊網絡模型；然后在滿足制造服務網絡的服務水平下分別考慮每個環節的資源動態配置問題，提出基于排隊論的近似公式；最后通過數值算例分析與仿真驗證檢查算法的有效性。本研究可為面向應急裝備的制造服務網絡提供資源配置的理論依據和管理建議。

1 問題描述與模型構建

面向應急裝備的制造服務網絡的動態資源配置需考慮客戶需求到達的高波動性及客戶需求的時效性特點。應急裝備制造服務網絡的耦合性質使得每個制造服務環節的資源配置存在較大難度。本節將基于時變排隊網絡理論對應急裝備制造服務網絡進行分析，針對服務資源動態配置問題構建數學模型并提出求解算法。

1.1 問題描述

考慮一個以應急裝備核心制造商主導上下游企業的外包型制造服務網絡，其中核心制造商包含收貨理貨、加工制造以及包裝運輸三個環節，首先由核心制造商收貨理貨，再根據生產計劃聯合生產承包商執行制造服務，最后由核心制造商集中完成包裝運輸。

當客戶隨機產生制造需求后，會由下游制造商向核心制造商訂貨，訂單資金流由下游制造商指向核心制造商；核心制造商會將原材料需求發送至上游制造商，訂單資金流由核心制造商指向上游制造商；同時核心制造商為了提高自身效益會將非核心業務外包給生產承包商，訂單資金流由核心制造商指向生產承包商。信息流存在于兩兩交互的制造網絡各成員企業之間。上游制造商為下游制造商提供制造服務，其間原材料和在制品等產品方向則與訂單資金流方向相反，如圖1所示。

為有效控制制造服務網絡的運營成本，制造商會提高資源利用率，不會超額配置制造服務資源數量。當制造服務環節資源不足時，產品會出現等待現象從而在緩存區內滯留，而產品等待時間過長會導致客戶取消制造需求，即產生客戶放棄制造服務的行為。為滿足每個制造服務環節的服務水平，即客戶放棄比例不超過管理人員設置的目標值，筆者構建優化模型并設計求解算法來最優化配置制造服務資源。

1.2 模型描述

由于應急裝備制造網絡下游的訂單需求符合NHPP的性質，因此產品流從上游制造商向下游制造商的傳輸過程也具有相應的隨機波動性，每個制造服務環節在滿足服務水平的要求下都需最優化安排各自資源。當下游制造商有銷售需求時，會向核心制造商訂貨。核心制造商根據下游制造商的訂單信息向上游制造商購買原材料半成品等產品。核心制造商從上游制造商處將原材料等收貨理貨后，將非核心業務的生產環節外包給生產承包商，由其完成后再交回包裝運輸環節，產品經包裝運輸后送至下游制造商，每一個環節均存在緩存區供待加工產品暫存。

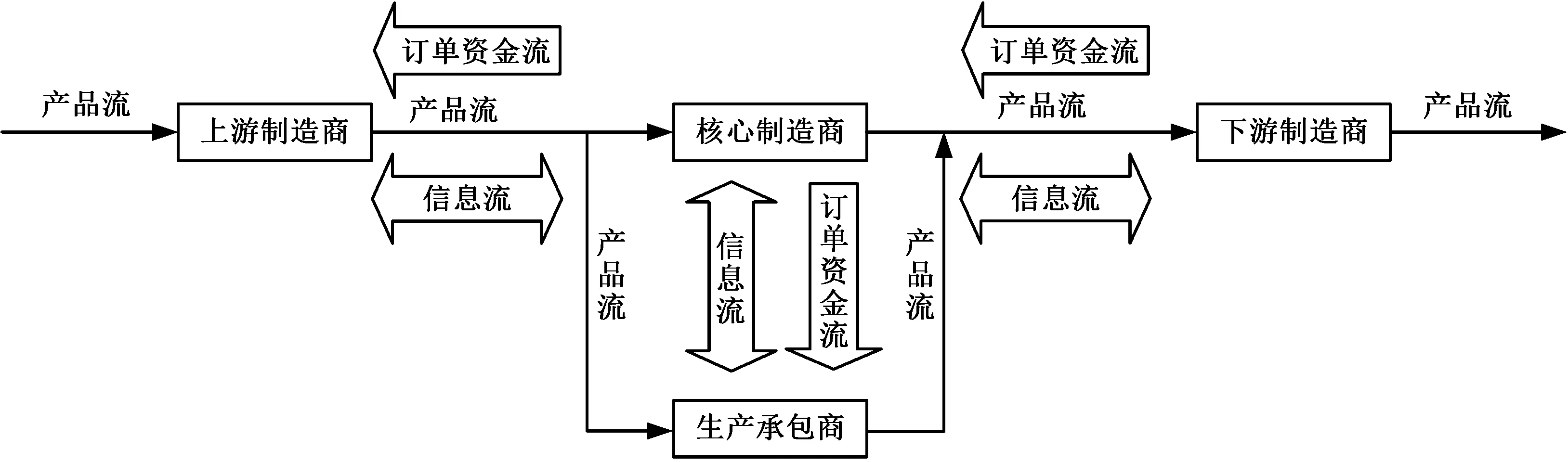
圖1 應急裝備SOMN結構Fig.1 Structure of SOMN for emergency equipment

結合圖1應急裝備SOMN中核心制造商和生產承包商的產品流，組成收貨理貨、自營制造核心業務、生產外包非核心業務和包裝運輸四個環節，構建如圖2所示的排隊網絡模型。圖2中，λi(t)為產品在時刻t到達制造服務環節i的速率函數；ξi(t)為時刻t客戶在緩存區i實際放棄的速率函數；σi(t)為時刻t產品在制造服務環節i完成后離開的速率函數；Qi(t)為時刻t產品在緩存區i的等待的產品函數；Bi(t)為時刻t產品在制造服務環節i所需的繁忙服務資源函數；p為概率。其中，i=1,2,3,4。i=1表示收貨理貨環節；i=2表示自營核心制造服務環節；i=3表示生產外包的承包服務環節；i=4表示包裝運輸服務環節。為使模型貼合實際應急裝備的加工過程，通過建立通用排隊網絡模型來表達服從一般分布的服務時間，并將排隊模型近似為8個無窮服務器(infinite server, IS)所組成的延遲服務器網絡(delayed infinite server network, DISN)模型。上游到達的產品承擔客戶的角色，核心制造商和生產承包商組成的4個環節所需配置的制造服務設施分別承擔服務器的角色。每一個環節的制造服務設施數量都是有限的，因此存在緩存區承擔隊列的角色，從而緩存區中的應急裝備超過一定時間將會導致制造需求的撤銷即客戶放棄現象。

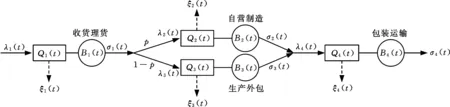
圖2 應急裝備制造排隊網絡結構Fig.2 Structure of emergency equipment manufacturing queueing network

服務型制造網絡中由核心制造商和生產承包商中的收貨理貨、自營制造、生產外包和包裝運輸4個環節組成了Mt/(GI,GI,GI,GI)/(st,st,st,st)+(GI,GI,GI,GI) 排隊網絡模型，前面4個GI分別表示4個環節的制造服務時間滿足一般獨立累積概率分布，后面4個GI分別表示顧客放棄等待時間服從一般獨立累積概率分布，4個st分別表示4個制造服務環節所配置的服務資源數量。產品流進入核心制造商的收貨理貨環節為到達速率函數λ1(t)服從NHPP，因等待時間超過耐心范圍后客戶的放棄速率函數為ξ1(t)，產品在收貨理貨環節完成服務后的離開速率函數為σ1(t)，假設自營核心業務進入核心制造環節的概率為p，即外包非核心業務進入生產承包商的概率為1-p。由此，產品進入核心制造環節的到達速率函數為λ2(t)=pσ1(t)，因等待時間過長造成客戶放棄的放棄速率函數為ξ2(t)，產品在核心制造環節完成制造服務后的離開速率函數為σ2(t)，隨即進入包裝運輸環節。產品進入生產承包商的到達速率函數為λ3(t)=(1-p)σ1(t)，因等待時間超期產生放棄的放棄速率函數為ξ3(t)，產品在生產承包商完成制造服務后的離開速率函數為σ3(t)，隨即進入包裝運輸環節。產品進入包裝運輸環節的到達速率函數為λ4(t)=σ2(t)+σ3(t)，客戶放棄速率函數為ξ4(t)，產品在包裝運輸環節完成服務后的離開速率函數為σ4(t)。

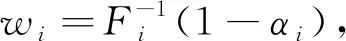
1.3 模型構建

基于1.2節建立的應急裝備制造排隊網絡模型，在不超過目標放棄比例的前提下，構建最小化制造服務資源配置數量的優化模型：

(2)

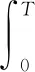
(3)

si(t)∈N0≤t≤T

(4)

i∈I,I={1,2,3,4}

式(1)表示目標函數為制造服務最小化配置數量；式(2)表示產品在緩存區中的放棄數量不能超過目標值εi，不等式左邊積分項為產品在緩存區中放棄事件的累計過程；在式(3)中由給定每一類緩存區中的目標放棄比例αi可算得目標放棄數量εi，不等式右邊λi的積分項為產品在制造服務環節i到達的累計過程；式(4)表示4個制造服務環節的資源配置數量均為非負整數N，時間取值范圍為0≤t≤T。

2 模型求解

由于1.3節的優化模型難以直接求解，可采用流體近似算法[19]進行分析。針對Mt/G/∞排隊模型，最早由EICK等[20]提出無限服務器(IS)近似算法計算繁忙服務器數量。針對考慮客戶放棄行為的Mt/GI/st+GI排隊模型，為了穩定隊列性能，LIU等[21-22]提出DIS流體近似算法求得服務器配置策略。針對核心制造商和生產承包商組成的服務型制造網絡模型，本文將收貨理貨環節構建為Mt/GI/st+GI排隊模型，而將自營制造環節、生產外包和包裝運輸環節均構建為·/GI/st+GI排隊模型，符號“·”表示到達過程是上游制造服務環節的離開過程。因此提出網絡結構的DISN近似算法分別對4個制造服務環節使用流體近似算法求解。

2.1 DISN近似算法

根據前文的應急裝備制造網絡結構，提出基于排隊網絡模型的DISN算法求解每個制造服務環節的資源配置數量。

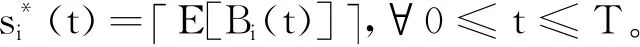
證明：

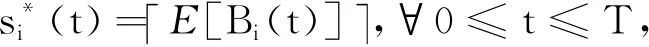
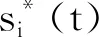
2.2 低QoS下的DISN-OL近似算法

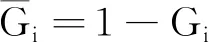
對于一個非負隨機變量Z，其均值為E[Z]，累積概率分布函數為H，H(x)≡P(Z≤x)。令Ze為服從He函數的隨機變量，He為H函數對應的剩余生命周期的累積概率分布函數，即

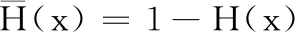
其中，隨機變量Ze滿足

E[Ze]=E[Z2]/(2E[Z])

定理2 對于應急裝備制造網絡結構為Mt/(GI,GI,GI,GI)/(st,st,st,st)+(GI,GI,GI,GI)的排隊網絡模型，產品到達速率為λi(t)。低服務水平即高目標放棄比例αi>0，則對應目標等待時間為wi>0，使用DISN近似算法求解制造服務環節所需配置的繁忙資源數E[Bi(t)]和緩存區中應急設備數量E[Qi(t)]的期望值：

(5)

(6)

證明：基于IS和DIS流體近似算法，提出的DISN近似算法用于求解排隊網絡結構的制造服務所需資源配置和緩存區中應急裝備產品的數量。構建Mt/GI/st+GI模型來近似處理·/GI/st+GI排隊模型。又將Mt/GI/st+GI模型拆成兩個Mt/G/∞串聯的排隊模型進行近似分析，因此在不同制造服務環節i的資源配置和對應緩存區內的應急裝備產品數量具有相同形式。

制造服務環節i的期望繁忙服務資源數量為

緩存區i內的應急裝備數量的期望值為

推論1制造服務資源可加性結合定理2可以推出核心制造商在包裝運輸環節的期望運輸設備數量可拆分成兩類不同產品分別計算，與直接計算聚合后所需期望繁忙運輸設備數量一致，即

E[B4(t)]=E[B41(t)]+E[B42(t)]

(7)

證明：核心制造商完成自營制造核心業務后產品離開的速率函數為σ2(t)，結合定理2計算自營制造完成后需要包裝運輸環節的期望繁忙設備數量E[B41(t)]；生產承包商完成生產外包非核心業務后產品離開的速率函數為σ3(t)，結合定理2計算生產外包完成后需要包裝運輸環節的期望繁忙設備數量E[B42(t)]，即

其中，(t-w4)+表示若t-w4小于0則取0，否則取正值。同時可得λ4(t)=σ2(t)+σ3(t)，即產品到達包裝運輸環節的速率函數等于核心制造商完成自營制造核心業務后產品離開的速率函數加上生產承包商完成非核心業務后產品離開的速率函數。

針對低服務水平QoS下即高放棄比例αi的應急裝備制造服務網絡的動態資源配置問題，本文提出DISN-OL網絡近似算法。由管理人員設置每個制造服務環節顧客的目標放棄比例αi>0，則對應緩存區內應急裝備產品的目標等待時間為wi>0。每個制造服務環節i的期望繁忙資源的數量為

(8)

對應緩存區i內的產品數量的期望值為

(9)

其中“∧”表示取小運算。當制造服務資源和對應緩存區內產品的數量在初始時刻t=0都為0時，利用定理2可求解每個制造服務環節的期望繁忙資源配置數量以及對應緩存區內的產品數量，其中，核心制造商在收貨理貨環節的期望員工數量為

(10)

核心制造商在收貨理貨環節的員工配置策略為

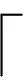
(11)

核心制造商在收貨理貨環節緩存區內產品數量的期望值為

(12)

核心制造商在自營制造環節的期望繁忙生產設備數量

(13)

核心制造商在自營制造環節的生產設備配置策略為

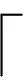
(14)

核心制造商在自營制造環節緩存區內產品數量的期望值為

(15)

生產承包商在生產外包非核心業務環節的期望繁忙制造設備數量

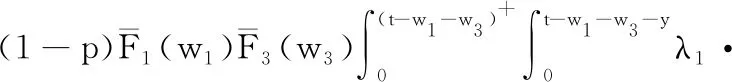
(16)

生產承包商在生產外包非核心業務環節的制造設備配置策略為

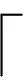
(17)

生產承包商在生產外包非核心業務環節的緩存區內產品數量的期望值

(18)

核心制造商在包裝運輸環節期望繁忙運輸設備數量

(19)

核心制造商在包裝運輸環節的運輸設備配置策略

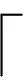
(20)

核心制造商在包裝運輸環節的緩存區內產品數量的期望值

(22)

DISN-OL近似算法對低服務水平QoS的求解非常有效，且具有數學解析式，但對高服務水平QoS下應急裝備制造網絡的資源配置問題用DISN-OL求解的效果并不理想，因此繼續用修正的DISN-MOL近似算法以滿足低目標放棄比例。

2.3 高QoS下的DISN-MOL近似算法

考慮應急裝備制造網絡的動態資源配置問題中帶有高服務水平QoS約束即低目標放棄比例αi，筆者進一步開發了DISN-MOL近似算法，該算法結合了單節點DIS-MOL近似算法和網絡結構DISN-OL近似算法。分別先由DISN-OL算法推出每個制造服務環節i所需的服務資源E[Bi(t)]，再轉化得到各制造服務環節的修正到達率

(23)

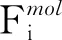
(24)

其中，δk表示當緩存區中有k個顧客時的放棄率，πj表示隊伍中有j個顧客的穩態概率。對于任意時刻t，遍歷搜索制造服務資源的最優配置數量，尋找最小非負整數si使得顧客的期望等待時間E[Wsi(∞)]≤wi。同時緩存區i內應急裝備數量的期望值為

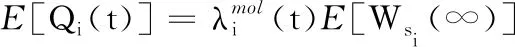
(25)

3 算例驗證

新型冠狀病毒肺炎(以下簡稱“新冠肺炎”)COVID-19在2020年爆發，引發了全球公共衛生重大事件。為防止疫情擴散，不同國家和地區分別采取居家辦公學習、減少公共出行、擴大核酸檢測等應對措施。隨著生產生活的逐步恢復，Morgen Stanley預測美國將在2021年春季爆發第二波疫情，如圖3所示，新冠肺炎患者確診人數具有時間波動性。在常態化疫情防控措施下，醫療衛生物資等應急裝備的需求呈現出相應的時序性特征，符合NHPP的假設。

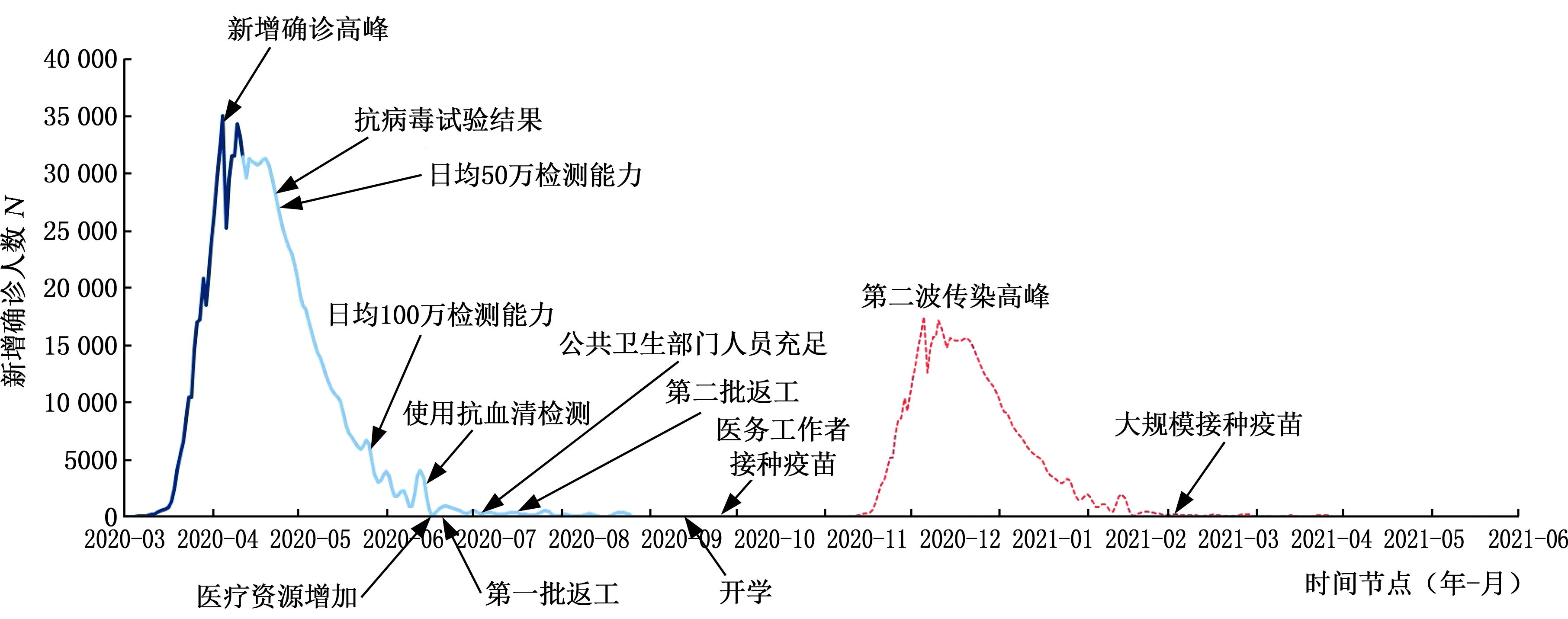
圖3 Morgen Stanley預測COVID-19在美國確診趨勢Fig.3 Diagnosis trend of COVID-19 in the US by Morgen Stanley prediction

在應急裝備制造服務網絡EE-SOMN中，相應的產品到達當前制造服務環節的過程服從NHPP。應急裝備產品到達的速率函數為正弦函數λ1(t)=a+bsin(c(t-φ))，表示在不同的時間范圍內產品到達的波動性[16-18]，T為計劃時間，φ為相位差。

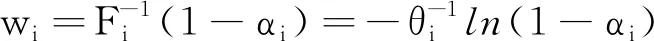
3.1 低QoS下的EE-SOMN系統

結合圖2的排隊網絡模型，研究低服務水平QoS下EE-SOMN系統。制造服務環節的目標放棄比例α1=0.15,α2=0.12,α3=0.12,α4=0.1，外部產品到達收貨理貨環節的速率函數參數為a=100,b=20,c=1,φ=π/2，每個環節的制造服務速率μ1=5,μ2=3,μ3=2,μ4=4,，每個環節的客戶放棄率θ1=1,θ2=1.5,θ3=1.5,θ4=2，自營制造核心業務的比例為p=0.6，則生產外包非核心業務的比例為1-p=0.4，四個制造服務環節分別為i=1,2,3,4，T=13表示最大計劃期為13個月。

假設外部產品到達收貨理貨環節的速率函數λ1(t)為正弦函數，每個制造服務環節的資源配置數量為si(t)。在圖4中，藍色實線si-alg(t)表示制造服務環節i資源配置數量的DISN-OL近似算法值，紅色虛線si-sim(t)表示在仿真中的實際取值。s1(t)表示在收貨理貨環節的員工配置策略，s2(t)表示自營制造核心業務環節的生產設備配置策略，s3(t)表示生產外包非核心業務環節的制造設備配置策略，s4(t)表示包裝運輸環節的設備配置策略。

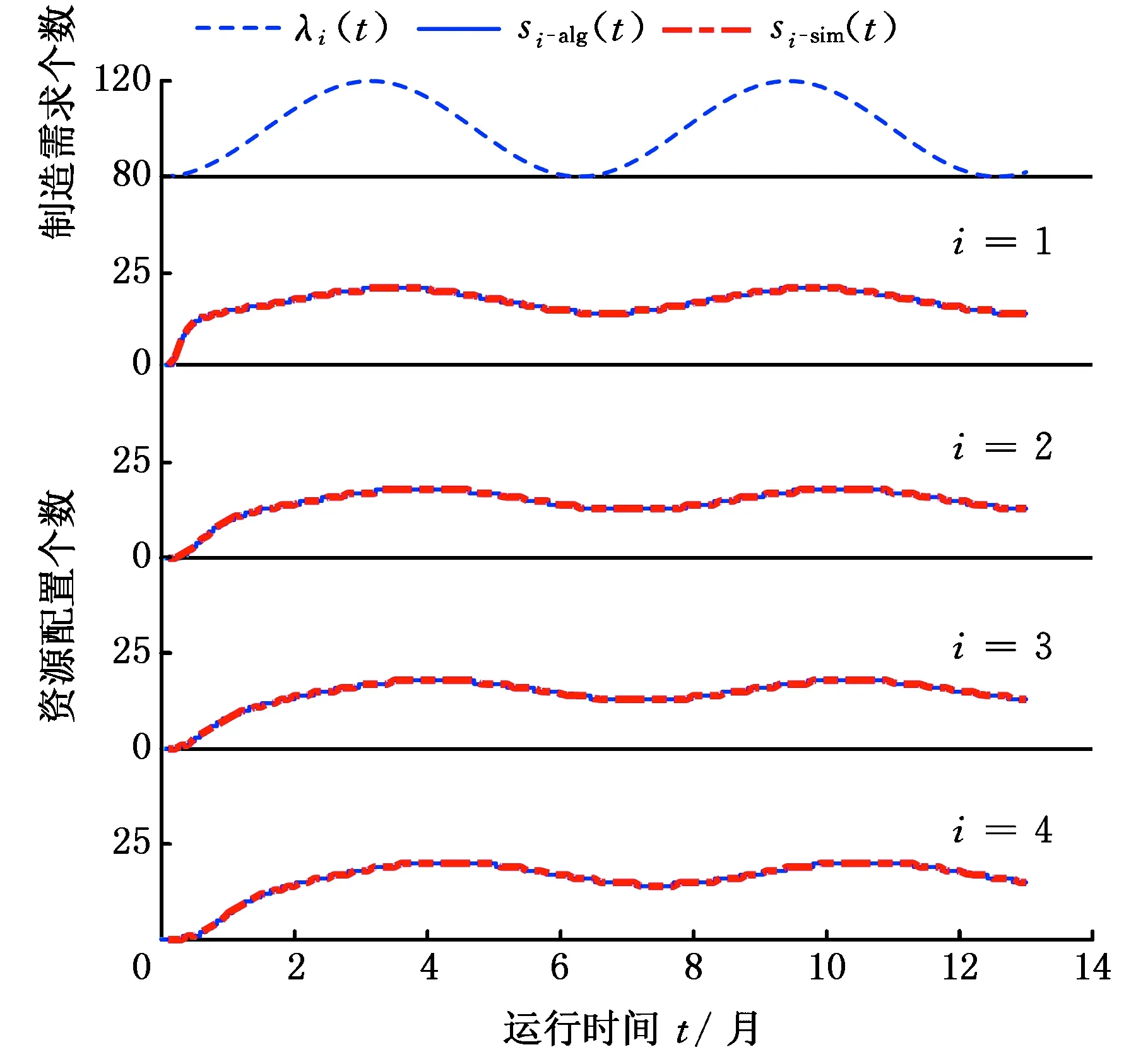
圖4 低QoS下資源配置數量Fig.4 Resource allocation under low QoS

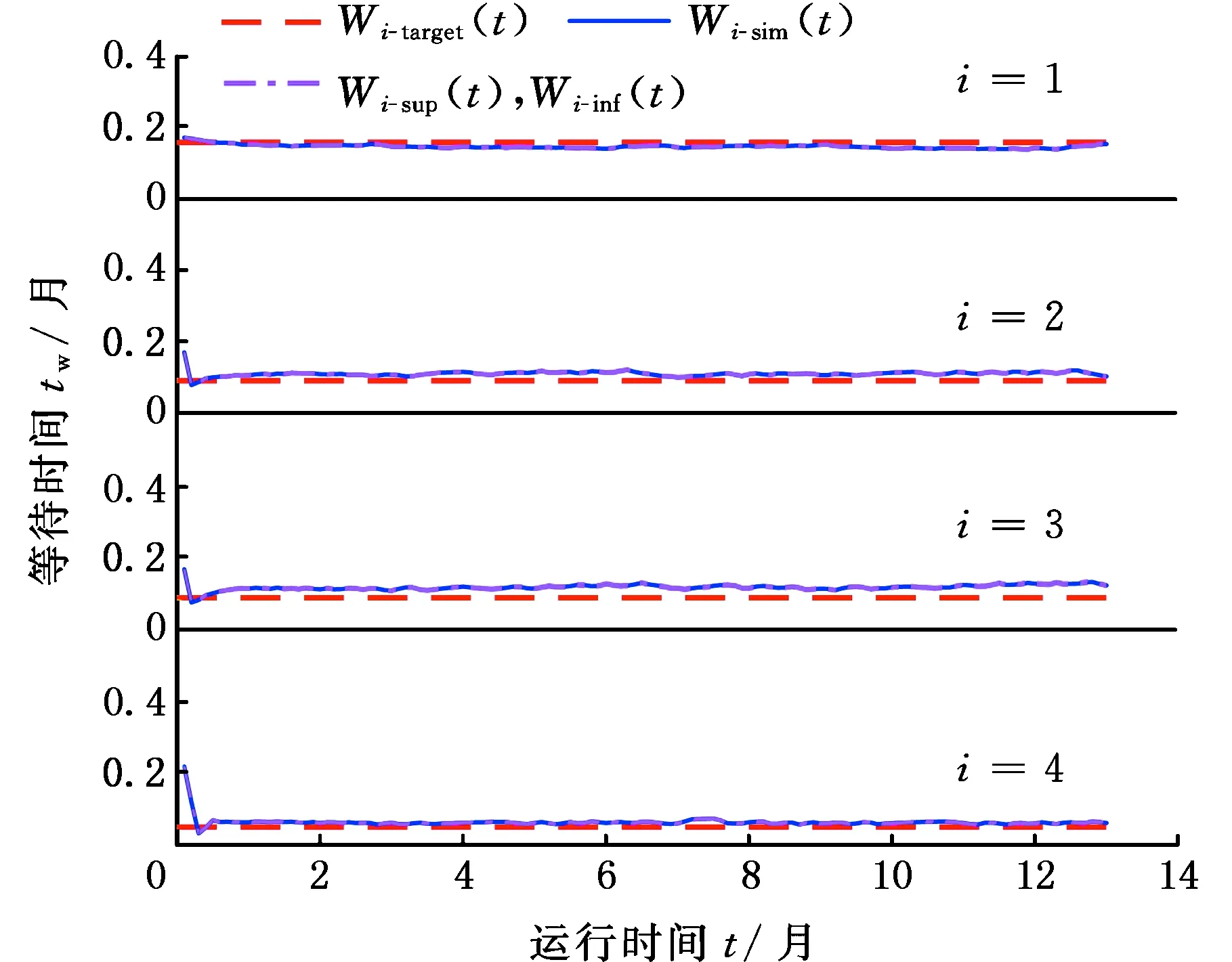
圖5 低QoS下顧客的期望等待時間Fig.5 Expected delay of customer under low QoS

針對低服務水平QoS下的應急裝備制造服務網絡，通過DISN-OL近似算法求解各制造服務環節的資源配置策略。圖5中對應緩存區內產品實際的等待時間Wi(t)都近似逼近目標等待時間wi，有效驗證了DISN-OL算法。在圖5的數值結果中存在初始下降現象，因為四個制造服務環節分別在時刻t=w1，t=w1+w2，t=w1+w3，t=w1+w4+min(w2,w3)開始配置資源，故算法仍然具有有效性。

通過DISN-OL近似算法求解各制造服務環節的資源配置策略，圖6中對應緩存區i內應急裝備產品實際的放棄比例PoAi都趨向穩定于目標放棄比例α1=0.15，α2=0.12，α3=0.12,α4=0.1，有效驗證，DISN-OL算法。

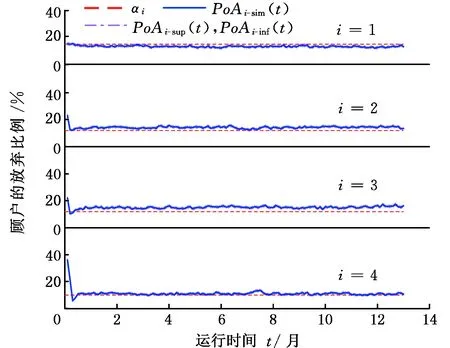
圖6 低QoS下顧客的放棄比例Fig.6 Abandonment probability under low QoS

3.2 高QoS下的EE-SOMN系統

結合圖2的排隊網絡模型，考慮高服務水平QoS下的EE-SOMN系統。四個制造服務環節的目標放棄比例分別為α1=0.05，α2=0.02，α3=0.02，α4=0.01；其他系統參數均同3.1節。

假設外部產品到達收貨理貨環節的速率函數同為λ1(t)，每個制造服務環節的資源配置數量為si(t)。圖7中紅線si-sim(t)和藍線si-alg(t)完全重合，說明制造服務資源在仿真中的實際取值由DISN-OL算法得到的資源配置近似值嚴格決定，從而驗證了在給定目標放棄比例αi下筆者提出的DISN-MOL算法的有效性。

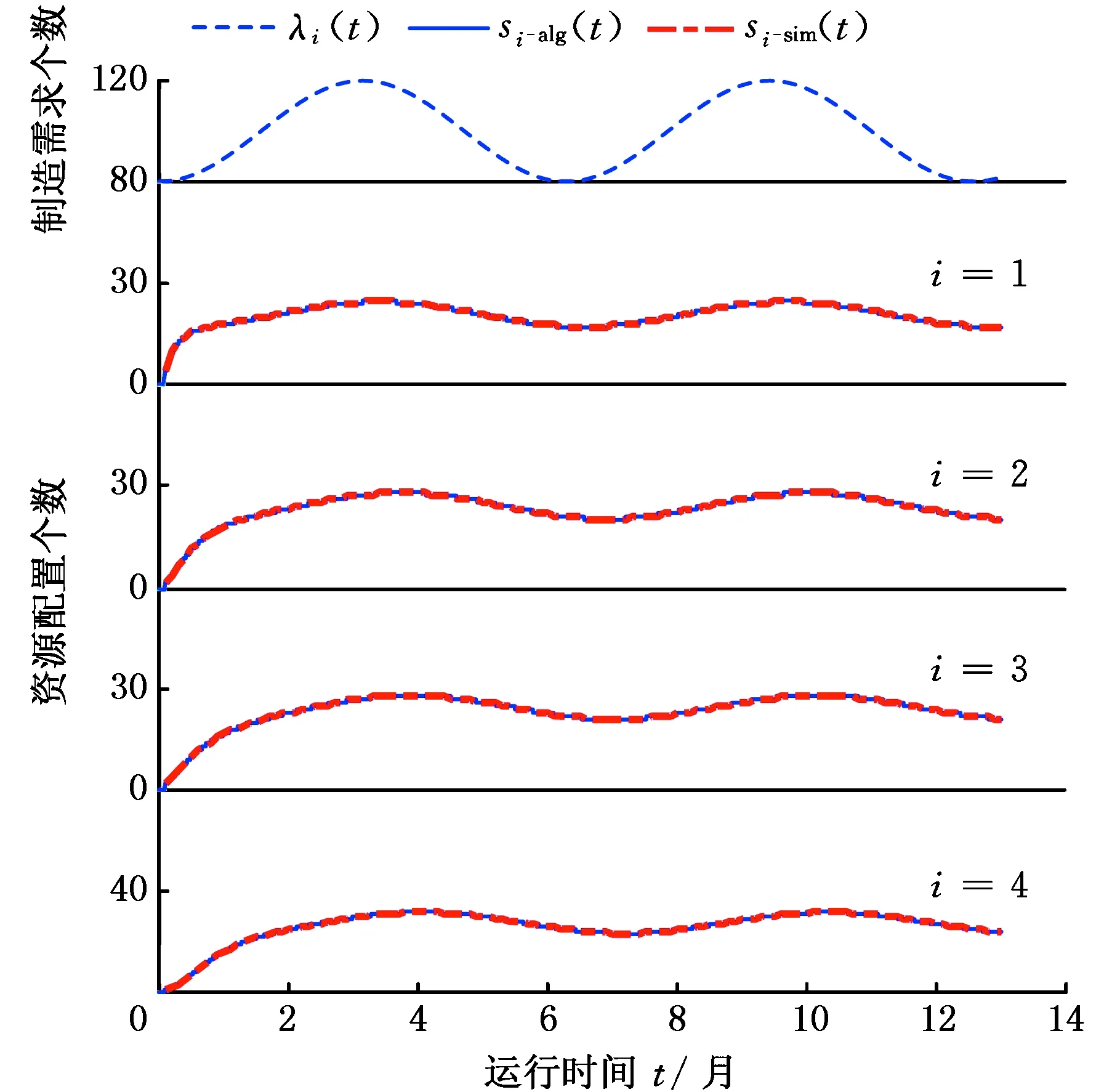
圖7 高QoS下資源配置數量Fig.7 Resource allocation under high QoS

針對高服務水平QoS下的應急裝備制造服務網絡，通過DISN-MOL改進算法求解各個制造服務環節的動態資源配置策略。圖8中緩存區內的產品實際等待時間Wi(t)都實現了不超過目標等待時間wi，有效驗證了DISN-MOL改進算法。因假設系統初始狀態為空，后3組曲線的開始階段實際等待時間先上升再穩定逼近目標等待時間，驗證了改進算法能有效配置資源。

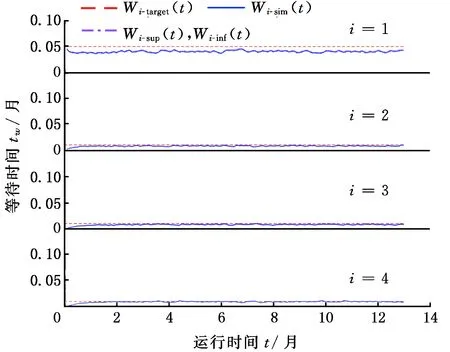
圖8 高QoS下客戶的期望等待時間Fig.8 Expected delay of customer under high QoS

通過DISN-MOL改進算法求解動態資源配置策略，圖9中每個緩存區內客戶實際的放棄比例PoAi(t)分別趨向穩定于目標放棄比例(α1=0.05,α2=0.02,α3=0.02,α4=0.01)，從而有效驗證了DISN-MOL改進算法。

圖9 高QoS下客戶的放棄比例Fig.9 A bandonment probability under high QoS

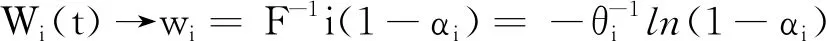
4 結束語

根據應急裝備制造網絡的高波動性和高時效性，本文建立了有客戶放棄的時變排隊網絡模型。基于排隊理論構造各制造服務環節的最小化資源配置策略，同時控制應急裝備的實際放棄比例低于目標放棄比例。針對低服務水平的應急裝備制造網絡提出DISN-OL算法，以及針對高服務水平的應急裝備制造網絡提出改進DISN-MOL算法，分別得到相應的制造服務資源配置策略。在數值算例中通過離散事件仿真驗證了兩種網絡近似算法的有效性。