基于脈沖漏磁暫態特征的缺陷量化評估方法

許 鵬 方 舟 王 平 耿 明 許 勇

1. 南京航空航天大學自動化學院，南京，211106 2. 工業和信息化部高速載運設施的無損檢測和監控技術重點實驗室，南京，211106 3. 中鐵第四勘察設計院集團有限公司，武漢，430063

0 引言

我國鐵路高速、高載和行車密度大，軌道安全問題日益突出。為了保障鐵路運行的安全，需對鋼軌缺陷進行長期、及時、高效的檢測與評估，而無損檢測技術具有非破壞性、包容性和動態性等特點，對鋼軌缺陷的檢測與評估有著至關重要的作用。目前，無損檢測技術已經從無損探傷(NDI)階段發展到無損檢測(NDT)階段，并逐步向無損評估(NDE)階段進行過渡，人們不僅希望能夠準確地對鋼軌缺陷進行識別，而且希望能對裂紋參數進行定量評估, 從而對鋼軌的運行狀態進行有效監測, 對損傷鋼軌進行相應的維護。 目前常見的鋼軌無損檢測方法有超聲檢測、渦流檢測、磁粉檢測和漏磁檢測等。超聲檢測是利用超聲波對金屬構件內部缺陷進行檢查的一種無損檢測方法,其穿透能力較強，能夠清晰有效地識別鋼軌的缺陷細節[1]，并對缺陷的縱向長度、傾角、深度等參數進行評估[2]，但存在需要耦合劑、直觀性差以及對近表面缺陷不敏感等缺點。渦流檢測[3]是一種基于法拉第電磁感應定律的電磁檢測方法，具有不需要耦合劑、檢測速度快的優點，但是只適用于金屬導體淺表面缺陷的檢測。磁粉檢測以磁粉做顯示介質對缺陷進行觀察，其檢測結果直觀，檢測成本較低，但需要磁懸液，目前磁粉已逐漸被磁敏傳感器所取代。相比于磁粉檢測，漏磁檢測精度高、速度快，操作簡便且無需耦合劑，在鐵軌、管道、鋼材等的缺陷檢測中得到了廣泛的應用。高運來等[4]、ANTIPOV等[5]通過漏磁檢測對鋼軌缺陷進行了量化評估。

脈沖漏磁(pulsed magnetic flux leakage，PMFL)檢測結合了渦流檢測和漏磁檢測技術的優點，采用脈沖信號作為激勵信號。經過傅里葉變換，脈沖信號可以分解為基波和一系列諧波信號之和，其中,低頻成分適用于檢測深層缺陷而高頻成分適用于檢測表面和近表面缺陷，因此脈沖漏磁檢測可以獲得豐富的缺陷信息[6]。目前，對缺陷的定量評估大多是對表面開口缺陷的寬度、深度和角度等參數進行評估[7]，很少有針對埋藏缺陷的評估方法，尤其是對埋藏深度(內部缺陷上表面到試件上表面的距離)和缺陷深度同時量化評估的研究更是接近空白，然而在實際的鐵路運營中，鋼軌缺陷包括滾動接觸疲勞裂紋、內部缺陷、壓潰、側磨、剝離等多種類型[8-9]，其中軌頭核傷會導致鋼軌發生突然脆斷，是最危險的鋼軌疲勞缺陷之一[10]。核傷起源于軌頭內部由于制造缺陷產生的細小裂紋，在列車運行荷載的反復作用下，這些細小裂紋先是成核，然后向軌頭四周逐漸擴大形成疲勞裂紋。對軌道表面和近表面傷損同時進行檢測和定量評估，對鐵路的安全運行有著重要意義。

徐中行等[11]、許鵬等[12]發現，由于存在渦流效應，激勵電壓和磁芯磁導率較小時，脈沖漏磁檢測信號存在過沖現象，并根據有過沖時的檢測信號對缺陷參數進行了定量評估。唐鶯等[13]也發現了類似的過沖現象。然而，為了得到較大的檢測信號，往往向激勵線圈施加較大的激勵信號，此時漏磁信號不會出現上述過沖現象[7,14-18]，因此，有必要尋找無過沖信號的新的特征量來對缺陷參數進行量化評估。一些學者研究發現，部分沒有過沖的漏磁信號在上升沿會出現上升速率減緩的波動現象[11,14-15,17]。本文基于脈沖漏磁檢測中漏磁信號沒有過沖的情況，同時對缺陷的深度和埋藏深度進行評估:使用ANSYS Maxwell軟件對脈沖漏磁檢測模型進行有限元建模與仿真，并根據仿真結果分析波動產生的原因;從脈沖漏磁信號的一階導數信號中提取兩個暫態特征量，并建立特征值與缺陷參數之間的函數關系，進而據此對表面和近表面缺陷進行定量評估;最后，用其他軌道缺陷樣本對該評估方法的準確性和可行性進行驗證。

1 脈沖漏磁檢測原理

脈沖漏磁檢測原理如圖1所示，探頭主要由激勵線圈、磁芯、被測樣本和磁敏傳感器組成。在檢測時，向激勵線圈施加脈沖激勵，從而磁化被測樣本。當樣本沒有缺陷時，由于樣本的磁導率遠遠大于空氣的磁導率，因此磁力線幾乎全部從樣本內部通過,當樣本表面存在缺陷時，缺陷處的磁導率減小、磁阻增大，導致磁場在缺陷附近發生畸變，部分磁力線從材料表面泄漏形成漏磁場。使用適當的磁敏傳感器便可檢測到漏磁場，并可將其轉化為電壓信號輸出。

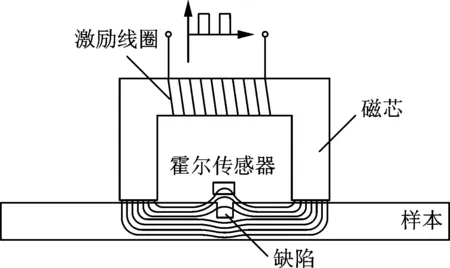
圖1 脈沖漏磁檢測原理Fig.1 Principle of PMFL detection

據法拉第電磁感應定律，磁通量的變化將產生感應電動勢和感應電流，因此當塊狀導體置于交變磁場或在固定磁場中運動時，導體內將產生閉合的感應電流，即為渦流現象。渦流具有趨膚效應，渦流密度衰減到其表面值的1/e時的透入深度稱為趨膚深度，其表達式為

(1)

式中，f為激勵頻率;μ為磁導率;σ為電導率。

由式(1)可知，趨膚深度隨激勵頻率的增大而減小，因此適當減小激勵頻率能夠提高檢測深度，而高頻信號更適合于對近表面缺陷的檢測。由于脈沖激勵包含一系列頻率分量，因此它可以在檢測遠表面缺陷的同時對近表面缺陷保持較高的敏感性。

2 脈沖漏磁檢測有限元建模與仿真

2.1 有限元模型

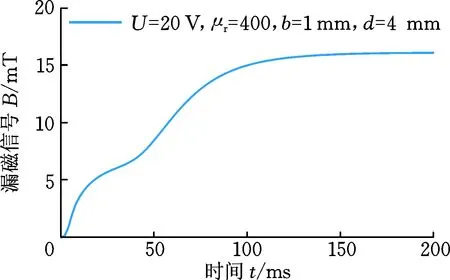
使用ANSYS Maxwell軟件建立脈沖漏磁檢測的二維瞬態仿真模型如圖2所示。該模型由缺陷鋼軌、磁芯和勵磁線圈組成。鋼軌導電率為4×106S/m，鐵心材質為鐵氧體，相對磁導率為400，導電率為0.01 S/m，繞組采用20 V方波激勵，方波周期為1 s，占空比為50%。如圖3所示，傳感器位于缺陷中心線右側1 mm，提離為1 mm，檢測Y方向的磁場。

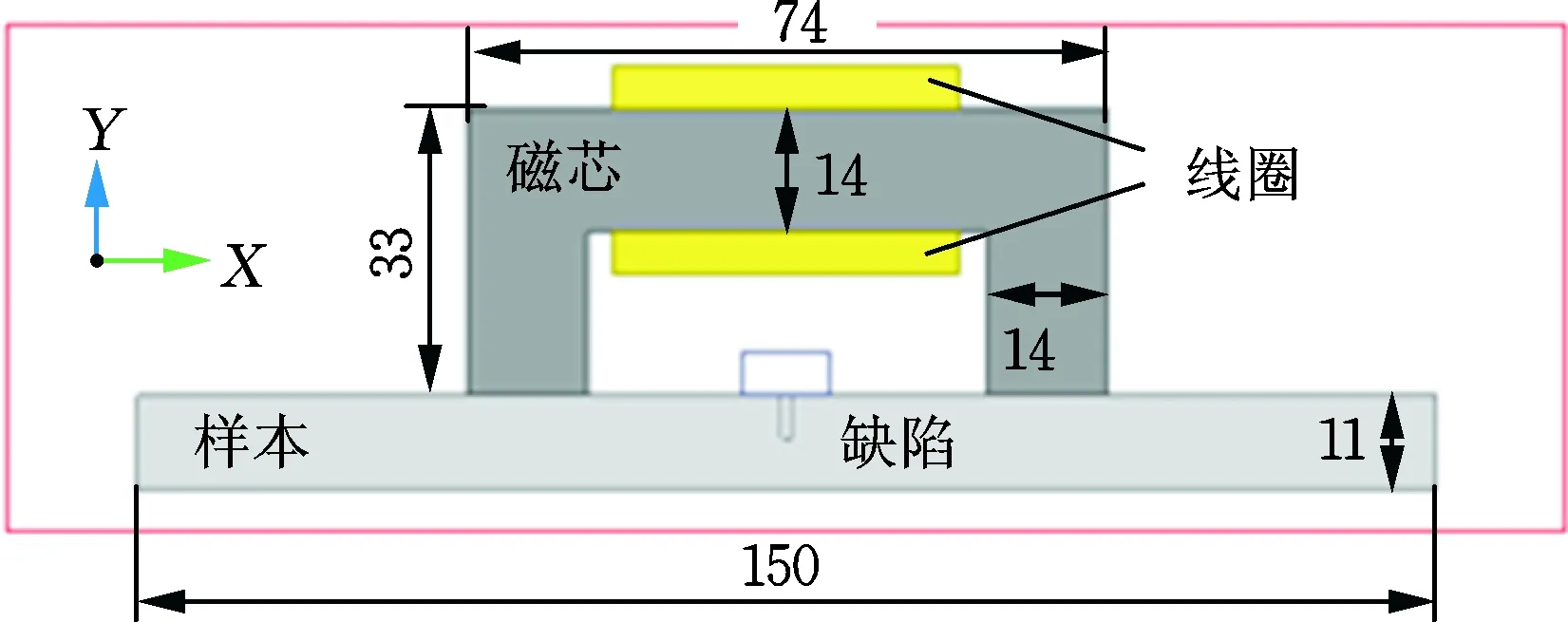
圖2 脈沖漏磁檢測仿真模型Fig.2 PMFL detection simulation model

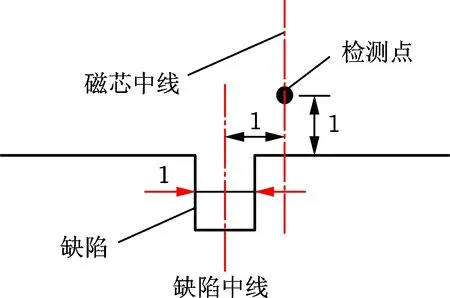
圖3 檢測位置示意圖Fig.3 Detection point diagram

2.2 渦流效應對檢測信號的影響

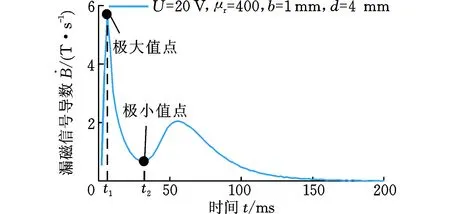
為了分析波動現象產生的原因，對相同的漏磁檢測模型進行兩次仿真，其中一次考慮渦流效應的影響，結果如圖4a所示。可以看出，在約10～40 ms的時間段，實線的上升速度減緩并出現波動，而虛線則未出現該現象。為了放大波動現象，繪制了漏磁信號的一階導數曲線，如圖4b所示。出現波動現象曲線的導數有兩個極大值點和一個極小值點，而沒有波動的曲線只有一個極大值點，沒有極小值點。由此可以說明，是渦流效應引起了曲線的波動現象。

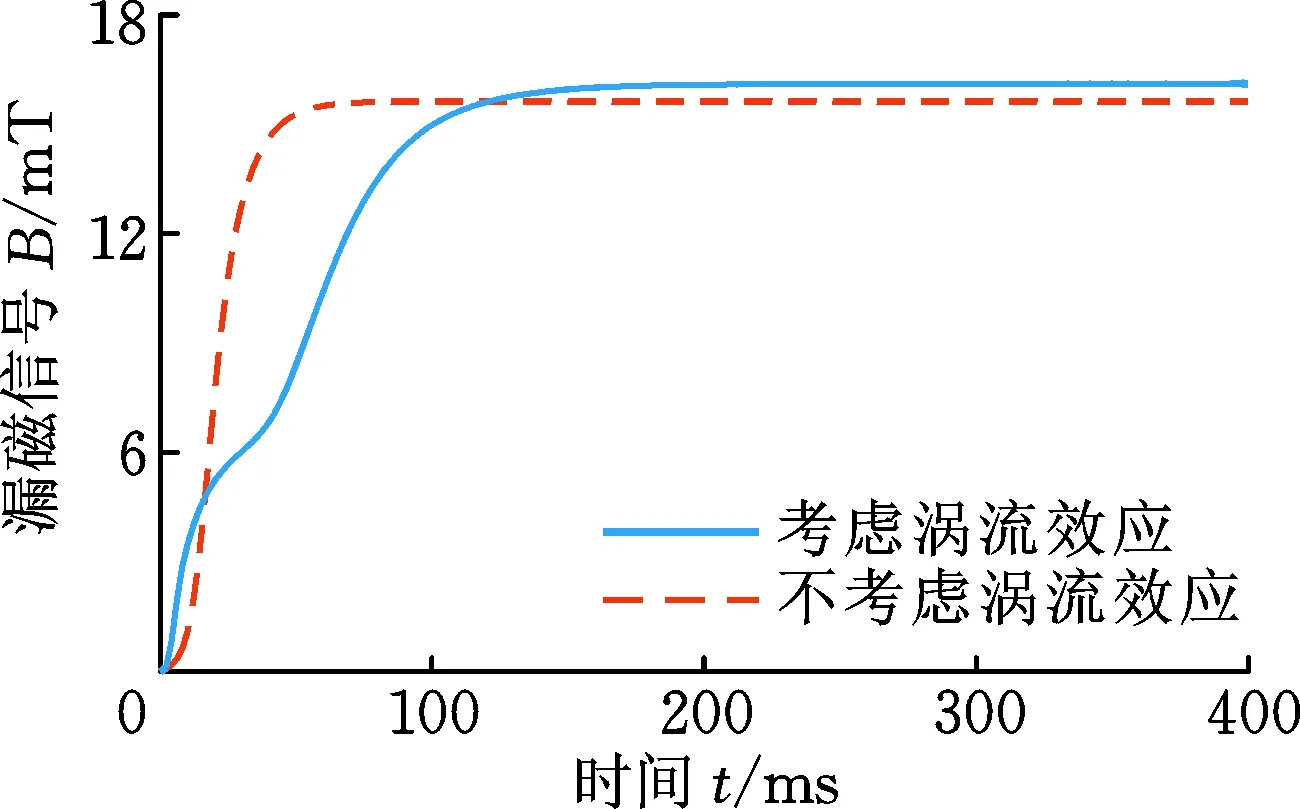
(a)脈沖漏磁信號

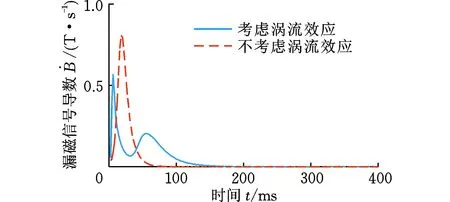
(b)脈沖漏磁信號的一階導數信號圖4 是否考慮渦流效應的信號比較Fig.4 Comparison of signals considering eddy current effect or not

當向激勵線圈施加激勵電壓時，電壓瞬間增大，此時樣本中的磁通量也由零開始快速增大。根據法拉第電磁感應定律，此時樣本中會產生渦流而阻礙原磁場的增大，因此渦流效應引起的磁場在內部與原磁場的方向相反。如圖5所示，假設施加激勵后樣本內磁力線方向向右，則由渦流效應產生一個向左的磁場(圖中虛線)。由于磁力線是閉合的，雖然在樣本內部由渦流效應產生的磁場的方向與原漏磁場方向相反，但是在缺陷正上方兩磁場的方向相同，兩者進行疊加導致漏磁信號增強，因此會出現過沖和波動現象。當電壓穩定后，磁通量不再發生改變，渦流效應逐漸消失，因此后來過沖和波動現象消失，磁感應強度最終趨于穩定。

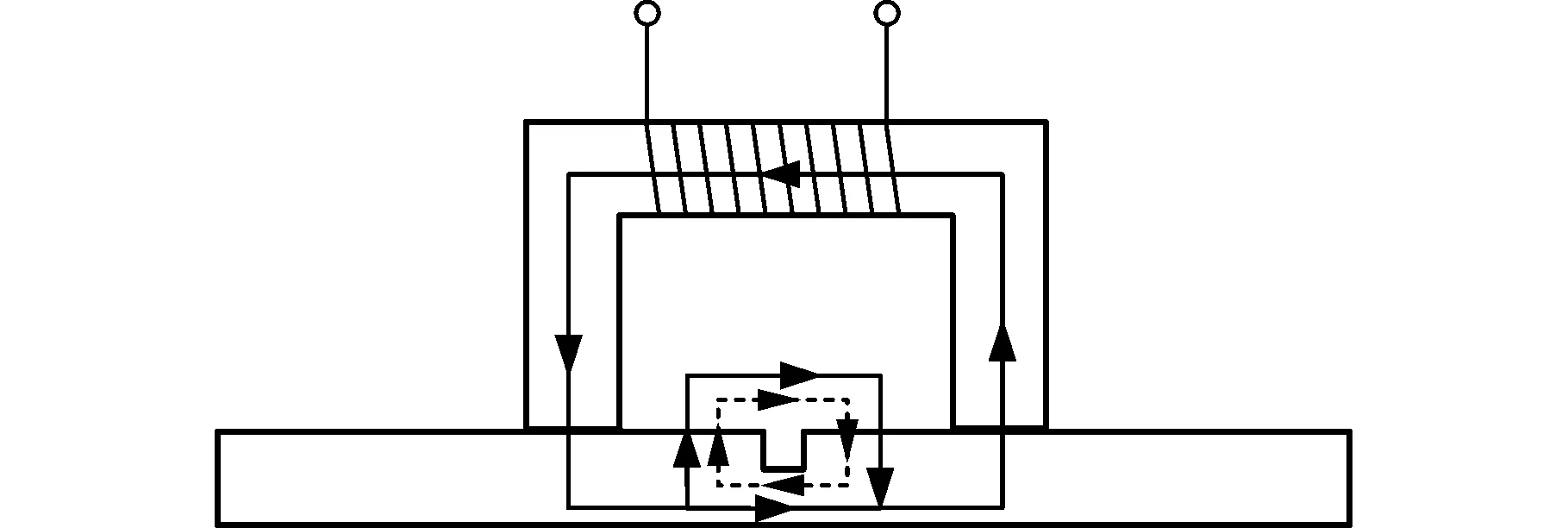
圖5 渦流效應對磁路的影響Fig.5 Effect of eddy current on magnetic circuit

2.3 激勵電壓和磁芯磁導率對檢測信號的影響

(a)脈沖漏磁信號

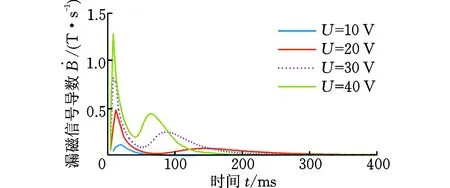
(b)脈沖漏磁信號的一階導數信號圖6 不同激勵電壓下的漏磁信號及其導數Fig.6 Magnetic flux leakage signal and its derivative in different excitation voltage

(a)脈沖漏磁信號

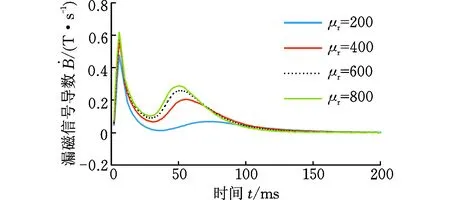
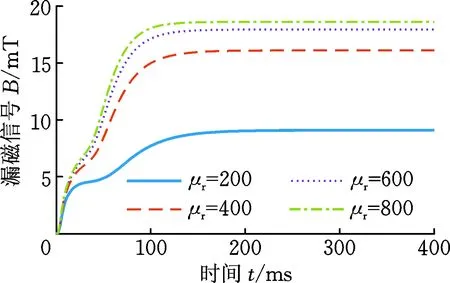
(b)脈沖漏磁信號的一階導數信號圖7 不同磁芯相對磁導率下的漏磁信號及其導數Fig.7 Magnetic flux leakage signal and its derivative in different magnetic core relative permeability

脈沖漏磁檢測信號不僅受到渦流效應的影響，還與激勵電壓以及激勵線圈磁芯的磁導率有關。圖6和圖7所示分別為在不同激勵電壓(U)和磁芯相對磁導率(μr)下的檢測信號及其導數。當激勵電壓和磁芯磁導率都較小時，原漏磁場較小，渦流效應產生的影響比較明顯，因此會產生過沖現象。而當激勵電壓和磁芯磁導率逐漸增大時，原漏磁場也逐漸增大，渦流效應的影響相對減小，此時過沖現象逐漸消失轉變為波動現象。當激勵電壓和磁芯磁導率足夠大時，上升階段的波動也將變得不明顯，憑目測很難觀察到。在以往的檢測過程中,為了使漏磁信號較大，所加激勵也較大，渦流效應的影響不夠明顯，因此沒有發現上述現象。但是這些信號的導數都有兩個極大值點和一個極小值點，證明了波動現象的確存在。

2.4 缺陷深度和埋藏深度對漏磁信號的影響

為了對不同缺陷深度和埋藏深度的軌道核傷進行評估，分析了缺陷深度d和埋藏深度b對脈沖漏磁信號的影響。缺陷深度d=6 mm，埋藏深度b變化時的脈沖漏磁信號如圖8所示。埋藏深度b=1 mm，深度d為2，3，…，8 mm時的缺陷信號及其導數如圖9所示。由圖8可知，上表面和近表面缺陷的漏磁信號出現波動現象，而埋藏深度為4 mm及以上的缺陷漏磁信號沒有出現波動現象。這是由于渦流具有趨膚效應，波動現象只能發生在表面及近表面的缺陷中。從圖9可以看出，深度越小，波動現象越明顯。

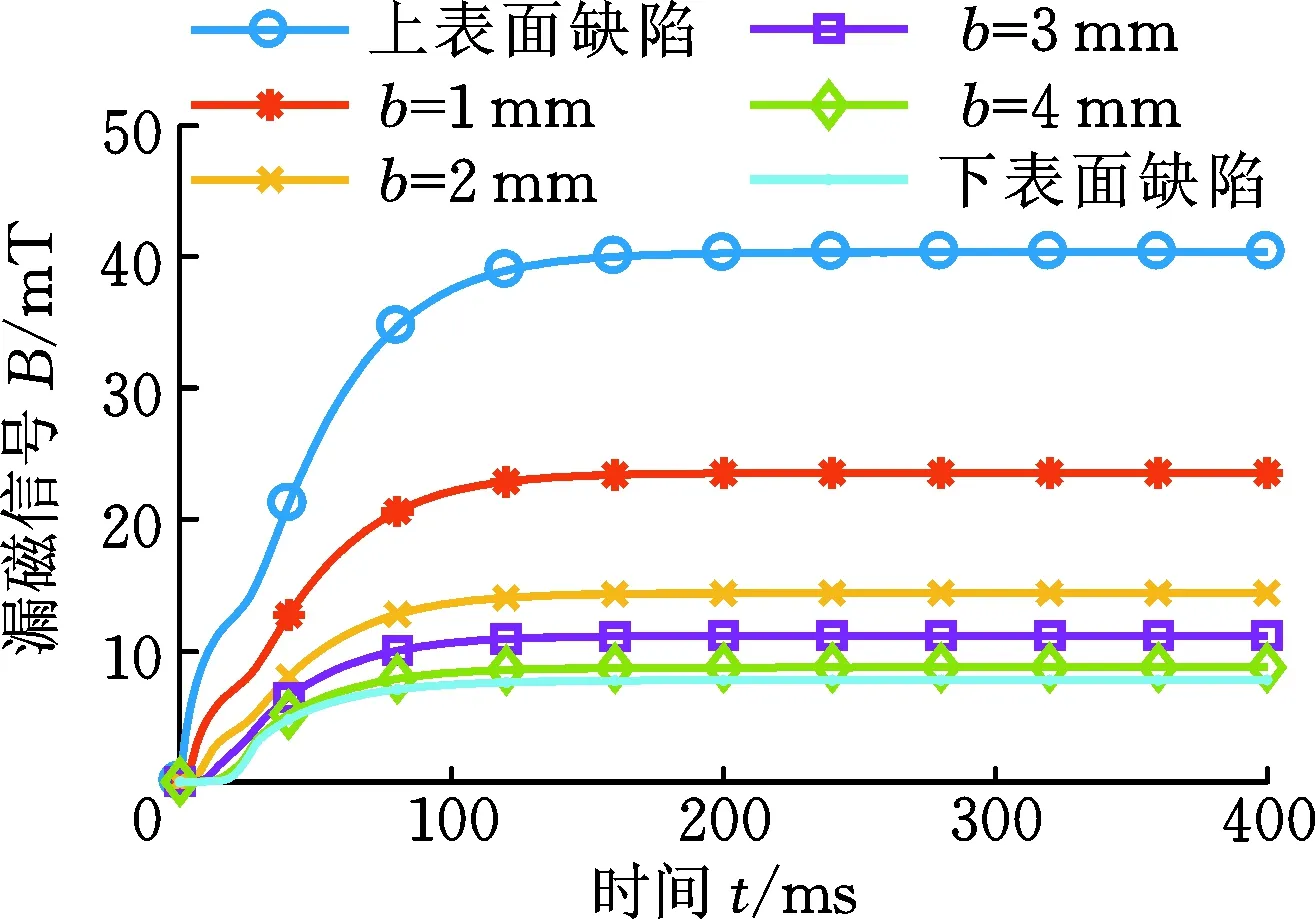
(a)脈沖漏磁信號

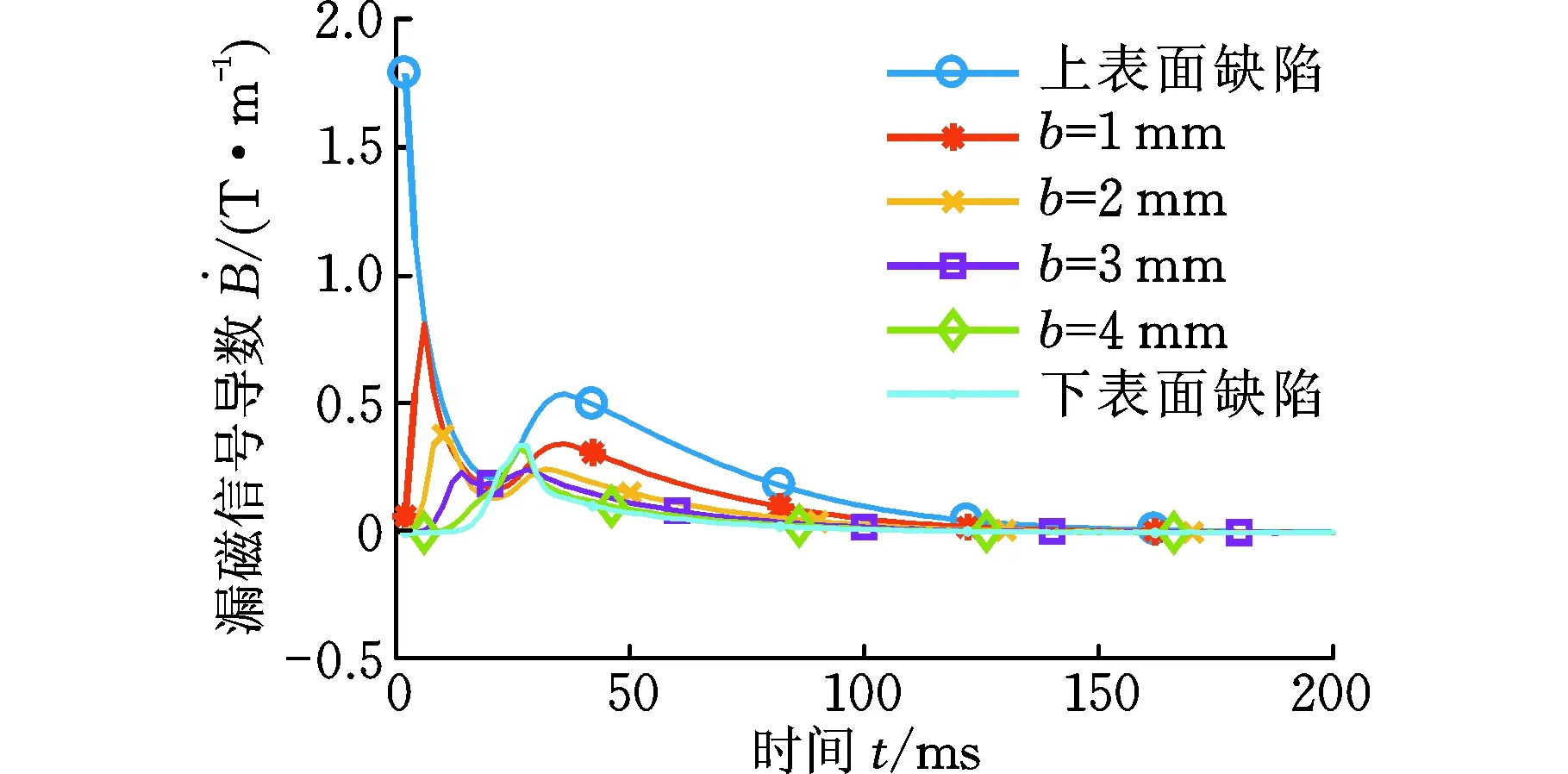
(b)脈沖漏磁信號的一階導數信號圖8 不同埋藏深度缺陷的漏磁信號Fig.8 Signals for defects of different burial depth

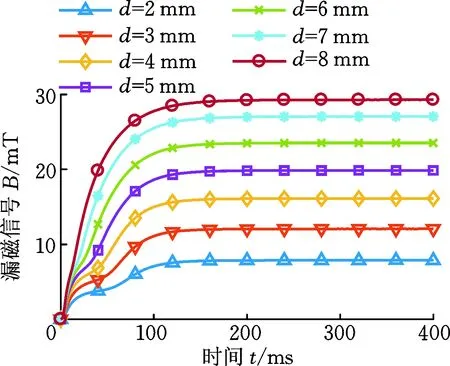
(a)脈沖漏磁信號

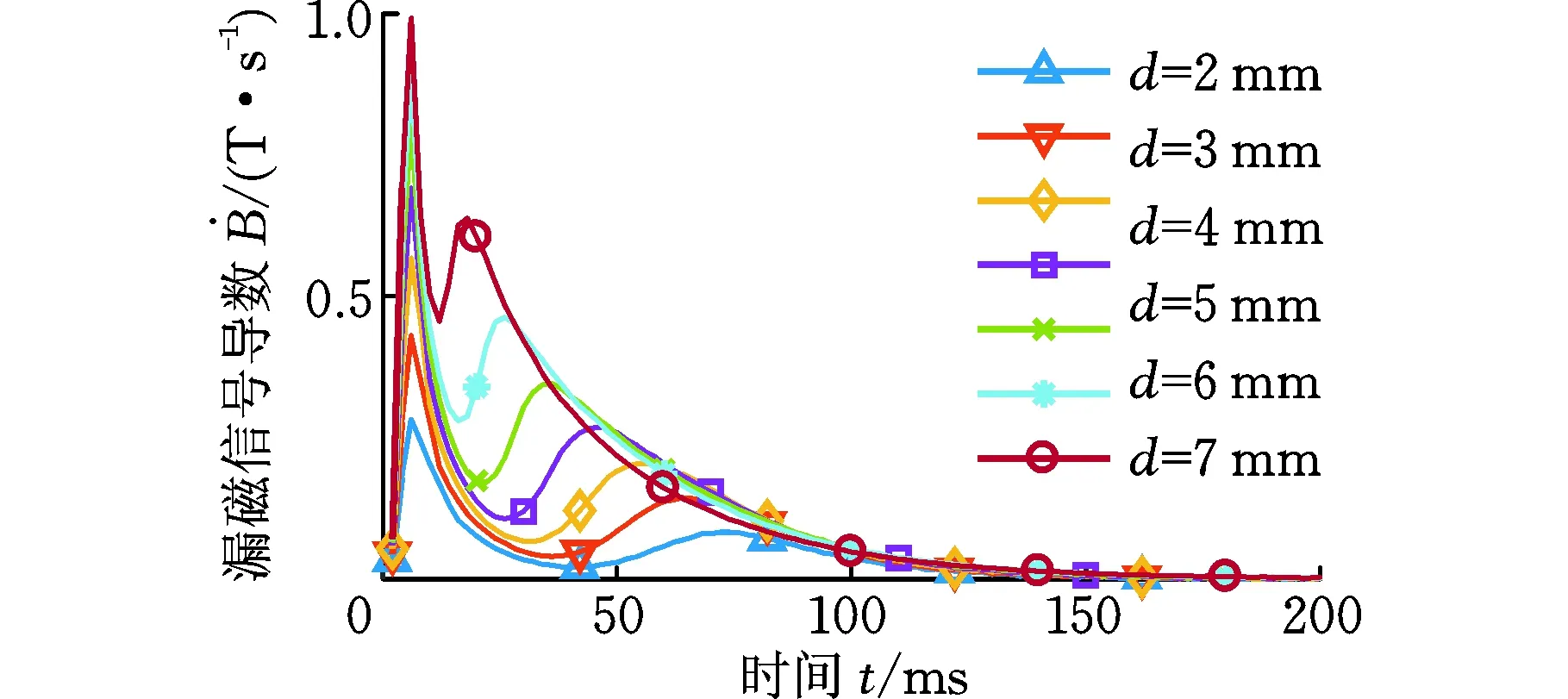
(b)脈沖漏磁信號的一階導數信號圖9 不同深度缺陷的漏磁信號Fig.9 Signals for defects of different depth

3 基于導數信號的缺陷量化評估方法

3.1 特征提取與缺陷評估

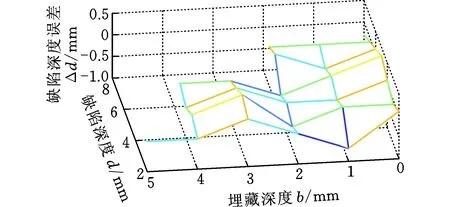
由于缺陷埋藏深度過大時漏磁信號不會出現波動現象，因此可以首先確定波動現象的出現范圍。仿真分析深度為2，3，…，8 mm，從上表面以1 mm步長向下移動至下表面的一系列缺陷，如圖10所示。可以看出，區域Ⅰ內缺陷的漏磁信號存在波動現象，區域Ⅲ內缺陷的漏磁信號沒有出現波動現象。區域Ⅱ中的缺陷由于仿真步長的限制，無法確定是否存在波動現象。受樣本厚度的限制，所有缺陷只可能出現在這三個區域內。

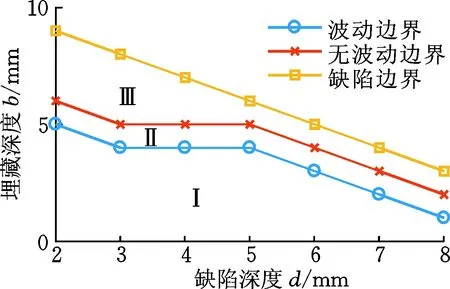
圖10 波動現象出現的范圍Fig.10 Range of fluctuations

(a)脈沖漏磁信號

(b)脈沖漏磁信號的一階導數信號圖11 極大值時間 t1和極小值時間 t2示意圖Fig.11 Diagram of maximum time t1 and minimum time t2

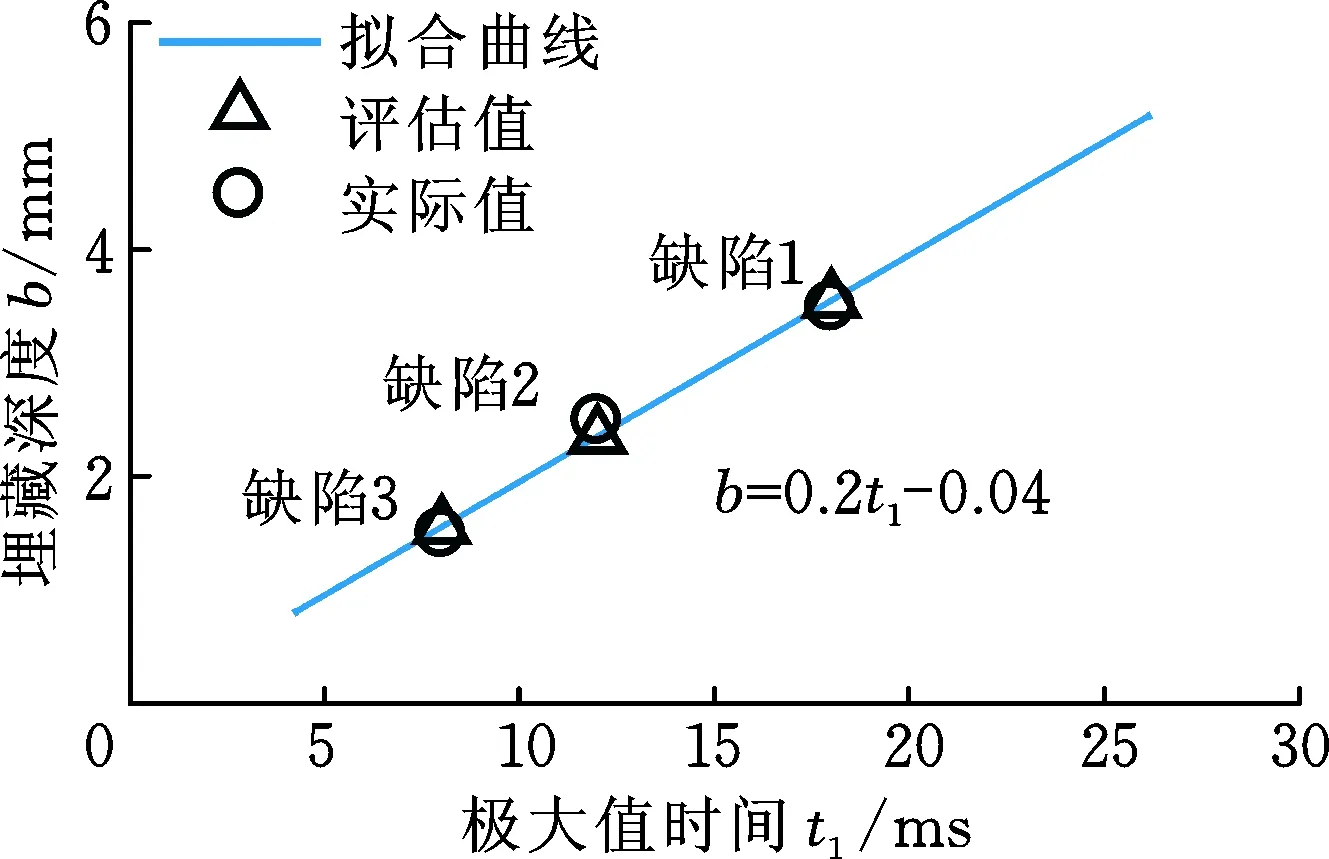
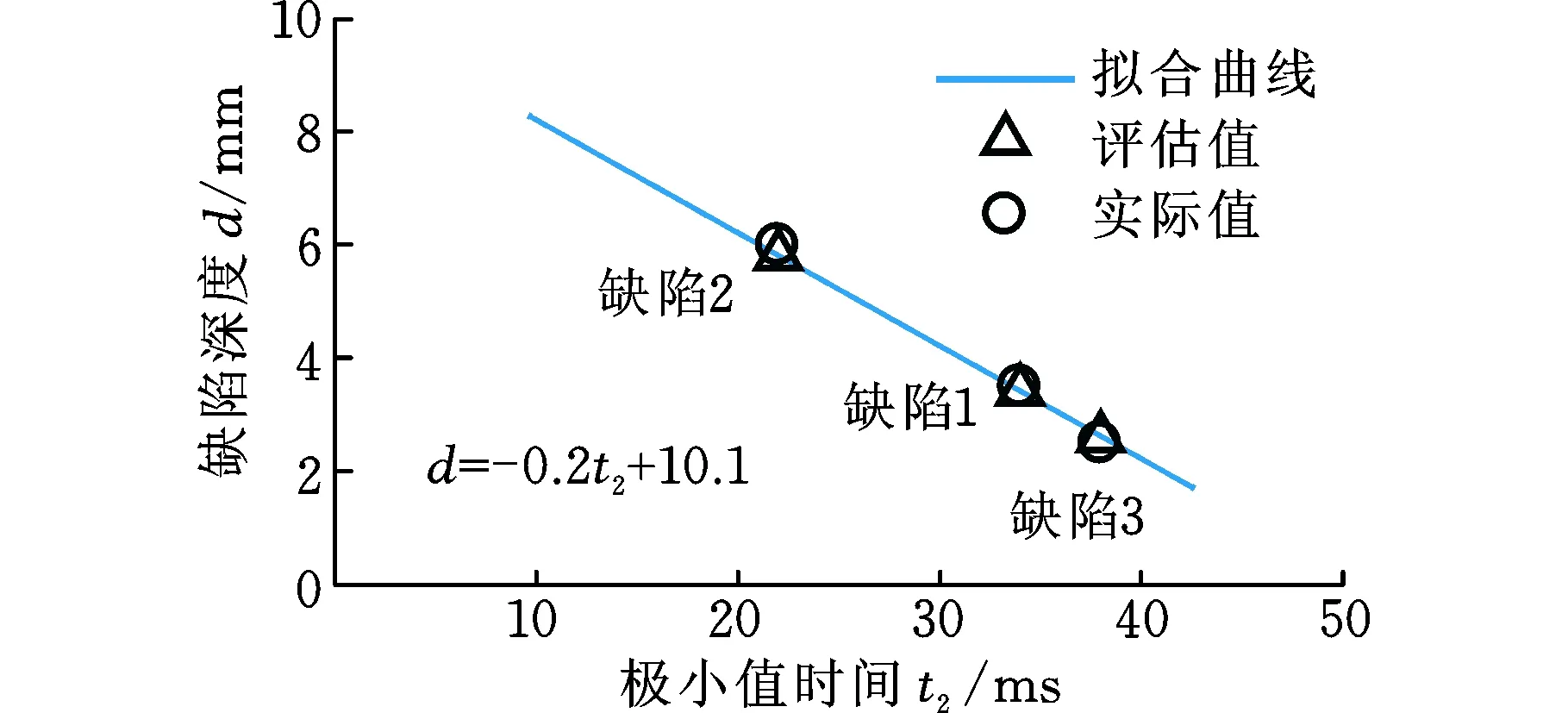
在實際的軌道檢測中，需要及時檢出軌頭核傷并對傷損尺寸、位置進行評估，從而對傷損鋼軌進行檢修維護，避免裂紋進一步擴展造成嚴重后果，因此本文研究了波動現象與缺陷深度及埋藏深度間的關系，以此對缺陷進行量化評估。以圖11為例，當漏磁信號出現波動現象時，從信號導數中提取兩個特征值：第一個極大值的出現時間t1和極小值的出現時間t2，各缺陷的t1和t2如圖12所示。從圖12中可見，在一定誤差范圍內，t1與埋藏深度近似成線性關系，與缺陷深度無關；t2與缺陷深度近似成線性關系，與埋藏深度無關。基于此線性關系，即可利用極值時間t1、t2對缺陷深度及埋藏深度進行量化評估，如圖13、圖14所示。分別用一次函數對b-t1及d-t2進行擬合，擬合函數為

b= 0.2t1-0.04

(2)

d=- 0.2t2+10.1

(3)

(a)缺陷深度 d、埋藏深度 b、極大值時間 t1三維圖

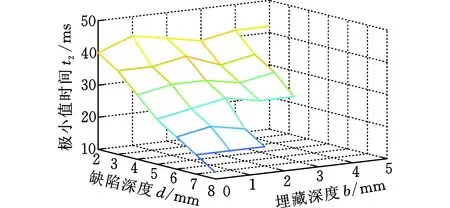
(b)缺陷深度 d、埋藏深度 b、極小值時間 t2三維圖圖12 缺陷參數與極值時間 t1、 t2的關系圖Fig.12 Relationship between defect parameters and extremum time t1, t2

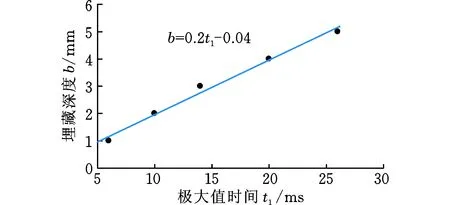
圖13 埋藏深度 b和極大值時間 t1的擬合曲線Fig.13 Fitting curve of burial depth b and maximum time t1

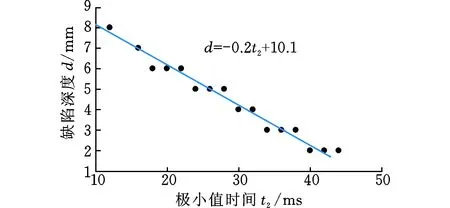
圖14 缺陷深度 d和極小值時間 t2的擬合曲線Fig.14 Fitting curve of defect depth d and minimum time t2

擬合值與真實值的誤差如圖15所示。分別計算每個缺陷擬合值與真實值的相對誤差，其中埋藏深度擬合值與真實值的最大相對誤差為10%，缺陷深度擬合值與真實值的最大相對誤差為16%。由此可以得到區域Ⅰ內軌道缺陷的量化評估方法：首先，采用脈沖漏磁方法對軌道進行檢測；其次，求取檢測信號的一階導數信號，并提取導數信號的兩個特征值(第一個極大值時間t1和極小值時間t2)；最后，分別將t1和t2代入式(2)、式(3)，即可同時評估缺陷的深度和埋藏深度。

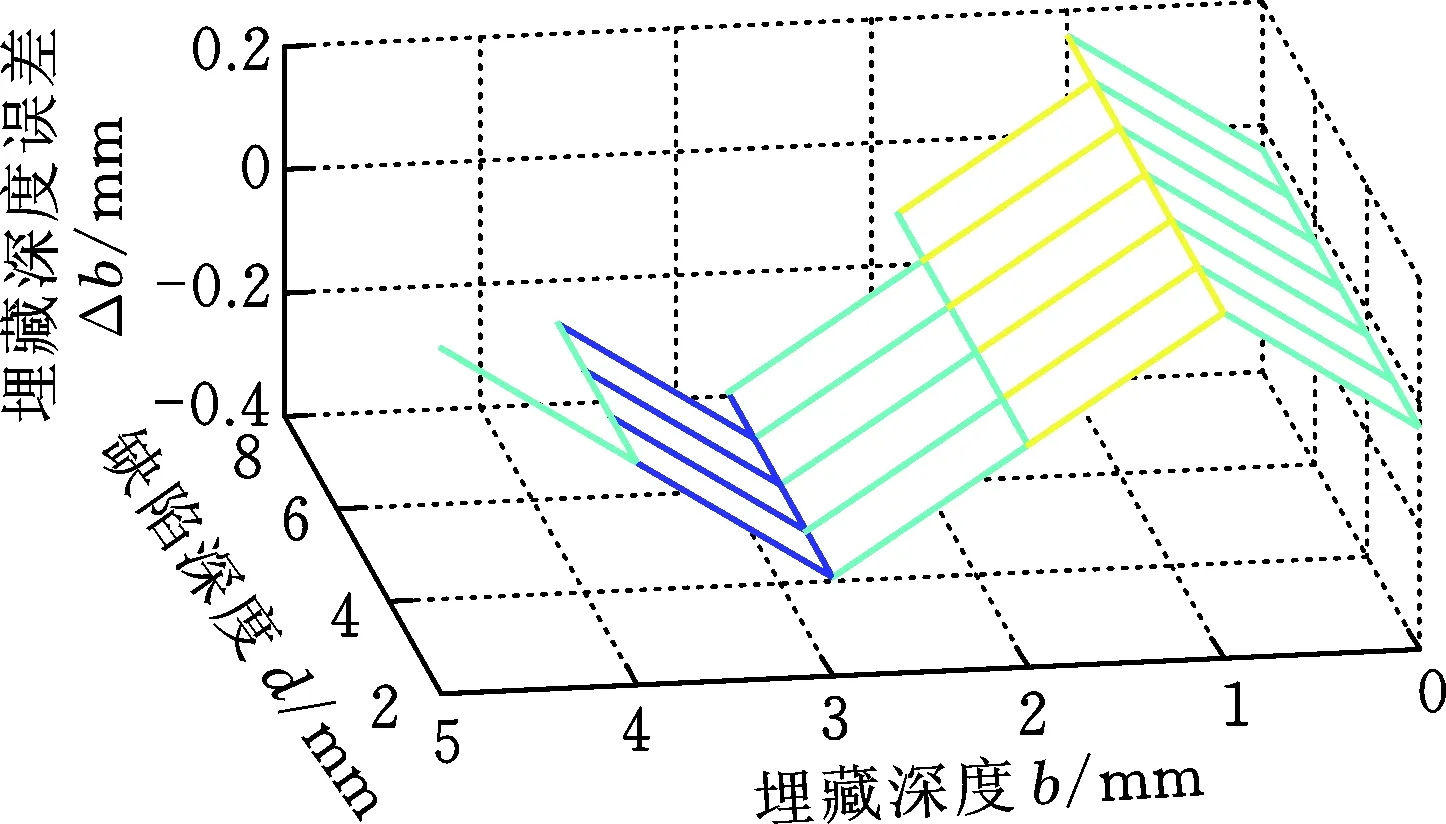
(a)埋藏深度的擬合誤差

(b)缺陷深度的擬合誤差圖15 埋藏深度和缺陷深度的擬合誤差Fig.15 Fitting error of burial depth and defects depth

3.2 方法的可行性分析

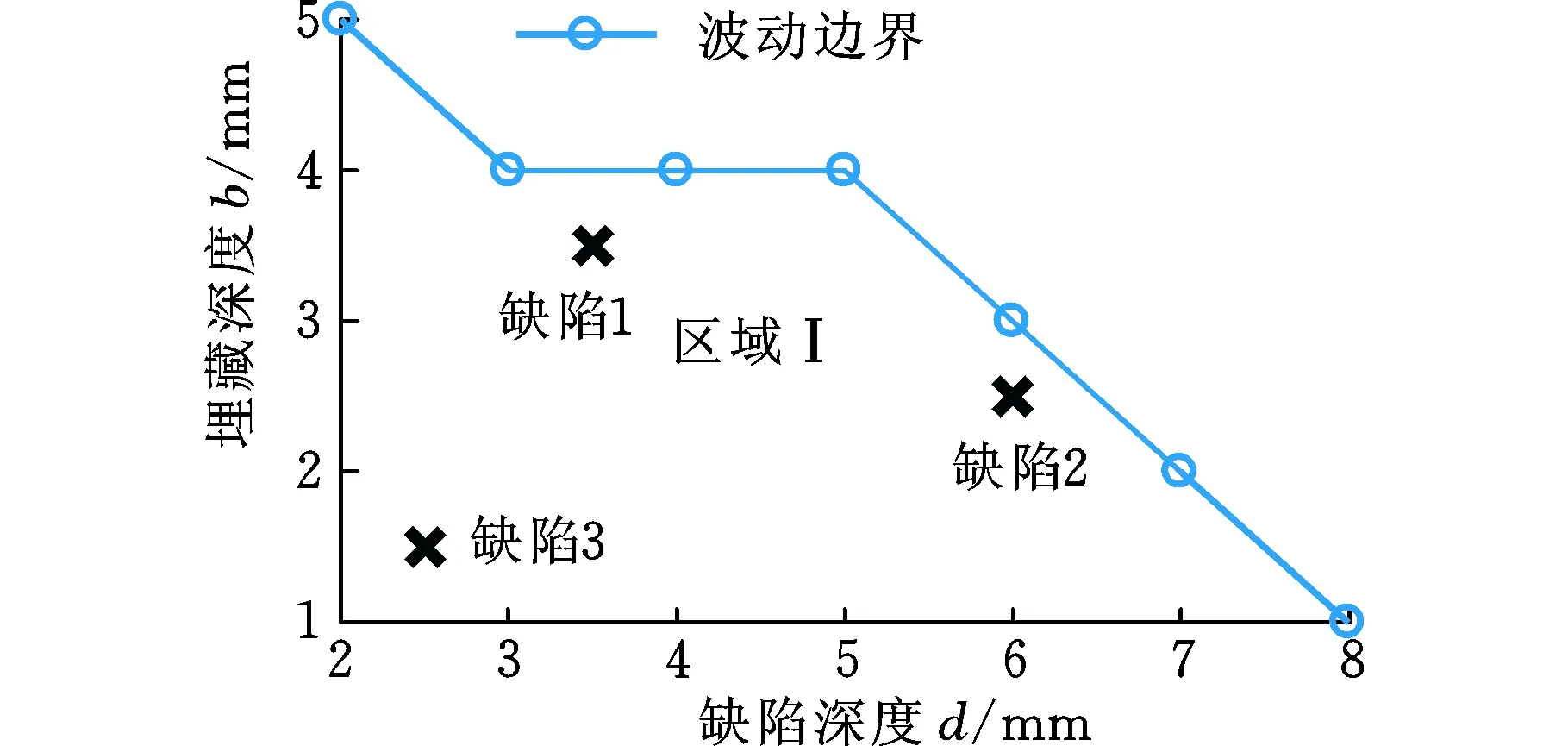
圖16 用于驗證的缺陷參數Fig.16 Parameters of defects for verification

(a)埋藏深度

(b)缺陷深度圖17 缺陷參數評估值與實際值Fig.17 Evaluation and actual data of defects

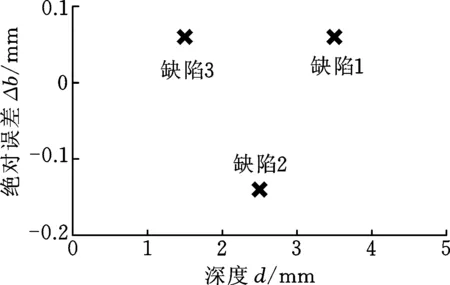
(a)埋藏深度b的誤差

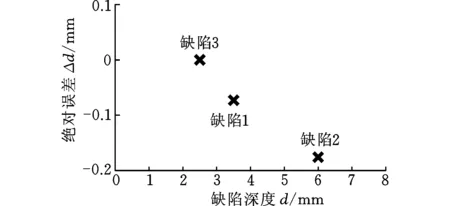
(b)缺陷深度d的誤差圖18 缺陷評估的誤差Fig.18 Error of defect quantitative evaluation

為了驗證上述方法的可行性，選取了三個新的已知參數的軌道缺陷樣本進行評估，如圖16所示。分別提取這三個缺陷脈沖漏磁信號導數的極值時間t1、t2，并將其代入式(2)、式(3)，得到對埋藏深度及缺陷深度的評估結果、量化評估值與實際值的誤差如圖17、圖18所示。結果表明，對于該三個樣本，本文所述評估方法得到的誤差均在0.2 mm以內，滿足鋼軌缺陷的量化評估要求。

4 結論

本文針對鋼軌核傷的無損檢測與量化評估問題，提出了一種同時對表面和近表面缺陷的缺陷深度及埋藏深度進行量化評估的方法。研究表明該方法適用于激勵信號或磁芯磁導率較大時出現波動現象的脈沖漏磁信號。通過對脈沖漏磁信號的一階導數信號的分析，從中提取了兩個特征值：極大值時間t1和極小值時間t2。分析了特征值與缺陷參數之間的函數關系，并研究了缺陷深度和埋藏深度的量化評估方法。最后，使用三個軌道缺陷的檢測信號進行驗證，缺陷參數的估計誤差均在0.2 mm以內，表明此評估方法是可行的。在之后的工作中，將研究動態檢測時基于脈沖漏磁信號特征的缺陷參數評估方法，并從檢測信號中提取更多用于評估缺陷參數的特征值。