基于時間序列分析方法的 廣州市月降水量分析

莊燕璇

摘要：本文基于廣州市1998年1月—2019年12月月度降水量數據，對序列進行建模分析和預測。基于AIC和BIC法則分別建立疏系數模型ARIMA（（4，5，6，7，8），1，1）和綜合分析模型Xt=StIt，兩種模型對2018年數據的擬合情況為：疏系數模的預測相對誤差小于50%的比例為33.33%;而綜合分析模型為58.33%。因此采用綜合分析模型對廣州市2020年降水量數據進行預測，預測得出廣州市2020年1月的降水量為54.686 mm，但隨著預測期的延長，預測精度降低。

關鍵詞：廣州市降水量序列;AIC;BIC;ARIMA模型;綜合分析方法

降水量是衡量地區干旱程度的一個重要指標，它直接反映了自然界的變化。降水量的多少直接影響農業生產，與現在農作物的生長周期和產量更是聯系密切。同時，降水量的年際變化趨勢直接制約著區域社會經濟發展和生態生活環境，影響著區域水資源的調配管理。通過對數據擬合建立一個不錯的模型進行短時間內較精確的預測，有助于安排農業生產，注意防范洪澇災害以及對水資源進行調配，具有重大的現實意義。

張吉英[1]利用沈陽市2005年至2016年的降水量資料，建立了ARIMA（1，1，1）預測模型對沈陽市降水量進行分析預測。張改紅[2]利用渭南市1953年至2013年的降水量資料，采用ARIMA模型對渭南市降水量趨勢進行模擬分析，建立最優降水量預測模型，該模型優點為短期預測精度高。呂志濤[3]利用鄭州市1971年至2013年降水量資料，分別采用了二次多項式擬合、諧波分析法以及自回歸模型構建了鄭州市降水量的預報模型，預報精度較高。

本文以廣州市為研究區域，利用1998年1月至2019年12月的廣州市降水量資料[4]，分別建立ARIMA模型和綜合分析模型對廣州降水趨勢進行分析，最后選擇最優模型進行預測應用。

首先基于AIC和BIC法則分別建立疏系數模型ARIMA（（4，5，6，7，8），1，1）和綜合分析模型Xt=StIt。接著根據模型對2018年的擬合結果選擇最優模型，發現此背景下綜合分析方法優于ARIMA模型。最后采用綜合分析模型對廣州市2020年的降水量數據進行預測。

本文的創新點在于分別選取了ARIMA模型和綜合分析模型對降水量數據進行分析，并通過對比預測效果挑選相對最優模型對2020年降水量進行預測。

1? ? 研究方法與理論分析

本章分為三節，第一、二節分別簡要介紹ARIMA和綜合分析方法的一般形式和建模步驟;第三節則給出模型精度評估方法。

1.1 ARIMA模型

1.1.1 ARIMA模型的一般形式

（1.1）

1.1.2 ARIMA模型建模的大體步驟

一、對初始時間序列進行平穩性分析，利用ADF檢驗對序列的平穩性進行檢驗[5]。

若初始時間序列平穩，則接著進行白噪聲檢驗;若初始時間序列不平穩，則對初始時間序列差分平穩化后進行白噪聲檢驗。

若檢驗結果顯示為非白噪聲序列，則擬合ARMA模型。

對擬合后的殘差序列進行白噪聲檢驗，若殘差序列為白噪聲，則說明初始時間序列的信息被充分提取，即模型較好;若殘差序列為非白噪聲，則需要重新進行擬合。

若ARIMA（p，d，q）模型中有部分自相關函數或部分平滑系數為零，那么該模型成為疏系數模型，記為ARIMA（（p1，...，pm），d，（q1，...qn））。

1.2 綜合分析方法

1.2.1 將序列進行混合模式分解

（1.2）

其中，Tt為趨勢效應擬合，St為季節效應擬合， It為隨機波動。

1.2.2 求出季節效應擬合

假定時間序列 周期長度為m，則季節指數的計算公式如式（1.3）所示。

（1.3）

其中為每個周期內的平均值，為總體均值。

1.2.3 對趨勢效應Tt進行擬合

對趨勢效應常用以自變量為時間t的冪函數進行擬合，即

（1.4）

1.2.4 對殘差序列擬合移動平均模型，以便充分提取相關信息

（1.5）

由（1.2）、（1.4）、（1.5）構造模型如下：

（1.6）

1.3 精度評估

本文用兩個準則來評估預報模型的精度。

一、相對誤差=，這是反映單個預測值精度的指標。

二、平均絕對百分比誤差這是反映一組預測值精度的指標。

其中，是時刻t的預測值，yi是時刻t的原始值，n是預測數。

2? ? 廣州月度降水量時序模型

2.1 ARIMA模型的應用

2.1.1 序列觀察

本文對1998年1月—2019年12月264個廣州月度降水量進行分析。本文用前240個數據參與建模，并用2018、2019年的數據檢驗模型的擬合效果，最后對2020年進行預測。

首先作時序圖如圖1所示。

由圖1可以看出該序列具有以下特點：有明顯的非零均值，有一定的周期性，周期為12個月，說明該序列是非平穩的。

因為降水量時間序列是非平穩時間序列，因此，我們先對初始時間序列進行差分平穩化后。

2.1.2 進行1階差分

首先對原序列χt做1階差分，得到序列▽χt，接著進行單位根檢驗判斷序列▽χt的平穩性。檢驗結果見圖2。

由圖2可以看出，該序列單位根檢驗的p值均小于0.0001。因此，在顯著性水平0.05下認為序列▽χt是平穩的。

2.1.3 擬合ARMA模型

根據2.1.2得出：序列▽χt是平穩時間序列。因此可以采用ARMA模型來擬合序列▽χt。根據BIC準則，本文選擇ARMA（8，1）模型來擬合序列▽χt。采用最小二乘法估計參數，因為模型ARMA（8，1）的一些參數不顯著，所以需要重新估計。接著，逐步剔除掉模型中不顯著的參數，直到模型剩下的參數均顯著為止。剔除的過程不在此處贅述，最后采用了無常數項的疏系數模型ARMA（（4，5，6，7，8），1）來擬合序列▽χt。參數估計見圖3。

由圖3可以看出，變量“MA1，1”、“AR1，1”、“AR1，2”、“AR1，3”和“AR1，4”的t檢驗的p值均小于0.05。因此，在顯著性水平0.05下可以認為這5個參數顯著非零。而變量“AR1，5”的t檢驗的p值為0.0537。因此在顯著性水平0.05下認為該參數不顯著而在顯著性水平0.01下是顯著的。權衡了擬合后殘差的白噪聲檢驗結果后決定將該參數加入模型中，即可用模型ARMA（（4，5，6，7，8），1）來擬合序列 。

2.1.4 模型的檢驗

為了檢驗模型對序列 的擬合效果，我們首先對擬合后的殘差序列進行白噪音檢驗，檢驗結果見圖4。

由圖4可以看出，白噪聲檢驗的p值均大于0.05。因此，在顯著性水平0.05下認為殘差序列為白噪聲，說明該模型的擬合效果好。

所以通過對1998年1月—2017年12月廣州降水量月度數據進行擬合并優化得到的具體模型是：

（2.1）

接下來需要通過比較模型的生成數據與現實的測度數據來觀察模型對廣州降水量的擬合效果。利用模型對2018年及2019年的廣州降水量月度數據做外推預報并計算相對誤差見表1。

由表1可以看出廣州市2018年實際降水量與預測值的相對誤差的平均值為1.23，而2019年為14.07。2018年相對誤差在30%以內的比例為33.33%，而2019年相對誤差在30%以內的比例為25%。因此，可以看出該模型對2018年降水量的擬合效果比2019年的好，從而可以看出，該模型不適用于長期預測。

從預測結果可以得出以下結論：第一，疏系數模型模型作為廣州市降水量預測模型是可行的;第二，該模型適合短期預測，隨著預測的延長，預測的誤差將逐漸增大。

2.2 綜合分析方法的應用

2.2.1 求出季節效應擬合

一、計算季節指數

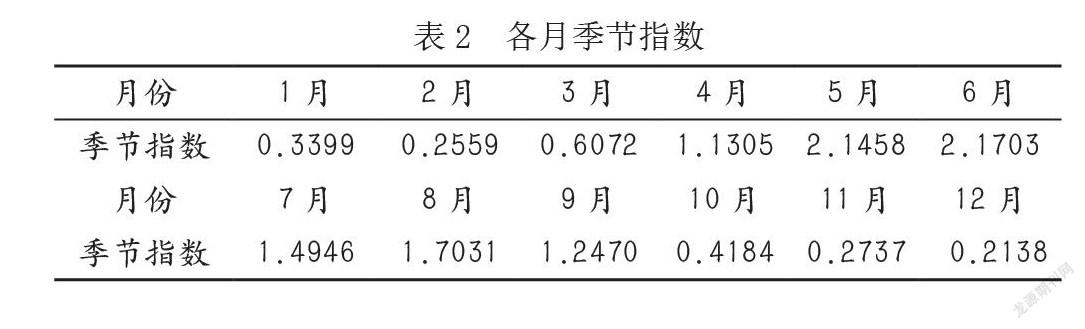
根據式（1.3）計算各月季節指數數據見表2。

由表2可看出，廣州降水量1月與2月較平穩，且降水量較少，3月—5月急速上升，5月—6月較為平穩，7月至12月呈現下降趨勢。其中1、2、3、10、11和12月的季節指數小于1，到12月時達到最低谷。4月—9月的季節指數均大于1，在六月達到最高峰。

3.2.2 對隨機波動It進行擬合

2.2.1節已求出季節效應擬合，下面以原時間序列值除以對應的季節效應擬合，得到的不包含季節效應的隨機波動的綜合值，即：，圖5為序列{Xt/St}的時序圖。

由圖5可以看出，序列{Xt/St}基本消除了季節性，且不具有趨勢性，可以初步判定序列{Xt/St}是平穩時間序列。

為了進一步的判斷序列{Xt/St}的平穩性，接著對其進行單位根檢驗，檢驗結果為在顯著性水平0.05下認為該序列是平穩時間序列。

2.2.3 對隨機波動 擬合ARMA模型

將隨機波動作為一個新的序列，按照1.1.2節介紹的方法建立ARMA模型來進行擬合，根據BIC準則：本文選擇ARMA（1，1）模型進行建模。

接著，我們采用無常數項ARMA（1，1）模型擬合隨機波動序列{Xt/St}，參數估計見圖6。

圖6? 隨機波動模型參數估計結果

由圖6可以看出，變量“MA1，1”和變量“AR1，1”的t檢驗p值均小于0.0001。因此，在顯著性水平0.05下認為該參數顯著非零。

隨機波動模型如下：

（2.2）

從而最終模型為：

（2.3）

2.2.4 模型檢驗

為了檢驗模型（2.3）的擬合效果，首先對擬合后的殘差序列進行白噪音檢驗，檢驗結果為在顯著性水平0.01下無法拒絕殘差序列為白噪聲。說明模型（2.3）提取信息充分，擬合效果較好。

為了對模型進行檢驗，下面利用模型對于2018年及2019年的廣州降水量月度數據做外推預報，得到的預報值見表3。

由表3可以看出廣州市2018年實際降水量與預測值的相對誤差的平均值為0.50，而2019年為7.00。2018年預測相對誤差在30%以內的比例為33.33%，而2019年預測相對誤差在30%以內的比例為25%。因此，可以看出該模型對廣州市2018年降水量的擬合效果比2019年的好，且該模型不適用于長期預測。

從預測結果可以得出以下結論：第一，綜合分析方法作為廣州市降水量預測模型是可行的;第二，該模型適合短期預測，隨著預測的延長，預測的誤差將逐漸增大。

2.3 兩種模型的對比與預測

根據2.1和2.2的分析，兩種模型均不適用于長期預測。因此，我們將根據兩種模型的短期預測效果即對2018年降水量的預測效果來判斷兩種模型的好壞，并用相對較好的模型來對廣州2020年的降水量進行預測。

2.3.1 兩種模型的對比

本文通過兩個角度來對比兩種模型，其一是兩種模型預測精度的比較;其二是預測結果的整體規律比較。

2.3.1.1 預測精度比較

由表1和表3可以看出，采用ARIMA模型擬合的2018年降水量的相對誤差低于50%的占比33.33%;而采用綜合分析方法預測的相對誤差低于50%的占比為58.33%，比ARIMA模型高出25%。因此，從預測精度看，綜合分析方法要優于ARIMA模型。

2.3.1.2 預測結果的整體規律比較

分別計算實際數據以及兩種模型擬合2018年降水量的平均數、中位數、極差，見表4。

由表4可得疏系數模型擬合值的平均數、中位數和極差與實測值的平均數、中位數和極差的差值分別均大于綜合分析方法。因此，從預測結果的整體規律看，綜合分析方法要優于ARIMA模型。

綜上所述，我們認為綜合分析方法更適用于擬合廣州市月降水量。

2.3.2 模型的預測

根據2018年1月—2019年12月觀測的實際值進一步修正模型后，得到廣州市2020年1—12月降水量預測值及其置信區間，見表5。

從對2020年的預測結果上看，廣州市降水量仍然延續以往的發展規律。2020年1月—2月降水量小且平緩，3月—6月急速增長且在六月達到最高峰，然后6月—9月總體呈現急速下降的趨勢，但是7月—8月降水量增加，在10月—12月降水量較小且變化平緩。

3? ? 結論分析與建議

本文基于ARIMA（（4，5，6，7，8），1，1）模型擬合廣州市降水量序列，所得到的模型BIC值為3001.104，AIC值為2980.245，而綜合分析模型為3048.52和3041.559。根據模型對2018年和2019年降水量數據的擬合結果得出兩種模型均只適用于短期預測。

最后根據模型對2018年的擬合結果選擇最優模型。兩種模型對2018年數據的擬合情況為：疏系數模的預測相對誤差小于50%的比例為33.33%;而綜合分析模型為58.33%。疏系數模型擬合值的平均數、中位數和極差與實測值的差值均大于綜合分析模型。因此，采用綜合分析模型（2.3）對廣州市2020的降水量數據進行預測，預測結果見表5。但隨著預測期的延長，預測精度降低。建議在使用綜合分析模型預測年降水量時，盡量保證數據序列足夠的情況下，采用逐年實時校正的預測方法。然后參考預測的結果做出相應的水資源調配以及防洪措施。

參考文獻

[1] 張吉英.基于ARIMA模型的沈陽市月降水量時間序列分析[J].內蒙古水利，2019（6）：13-14.

[2] 張改紅.基于ARIMA模型的渭南市降水量趨勢分析與預測[J].價值工程，2019，38（34）：197-199.

[3] 呂志濤.時間序列分析方法在鄭州市降水量預報中的應用[J].南水北調與水利科技，2014，12（4）：35-37，56.

[4] 國家統計局.中國統計年鑒（2020）[M].北京：中國統計出版社，2020.

[5] 王燕.應用時間序列分析[M].北京：中國人民大學出版社，2005.