區間值Choquet 積分及其性質

郭元偉

太原學院數學系，山西 太原030009

G.Choquet 于1955 年提出了容度及其積分理論［1］，Choquet 積分是一種基于非加測度的非線性積分，在圖像處理、模式識別、信息融合、數據挖掘、主觀評判、決策分析以及經濟學等領域［2～5］有廣泛的應用.Wang 研究了基于非可加測度實值Choquet 積分及其收斂定理［6］，在此基礎上Pedytcz 給出了Choquet 積分的平均收斂、等度可積、基本平均收斂等定義［7］，并討論了它們之間的關系. Guo 討論了集值測度的性質［8］，Jang 等研究了集值Choquet 積分的上、下極限［9］，Zhang 等指出并修正了上述文獻中的一些錯誤，并且證了Kuratowski 收斂定理［10］.Wang 和Li 討論了非負集值Choquet 積分的基本性質和集值Choquet 積分序列的收斂定理［11］.Jiang 和Wang 分別研究了區間值Choquet 積分［12］和單調集值Choquet 積分［13］，Wang等研究了模糊值Choquet 積分序列的基本性質［14，15］，并討論了一致收斂、平均收斂、積分有界之間的關系，進一步豐富了Choquet 積分.然而區間值函數的關于非加測度的Choquet 積分尚未見到討論.本文利用區間值函數和實值非可加測度的Choquet 積分，定義和討論了區間值函數關于非可加測度的Choquet 積分，并給出了轉換定理，討論了單調區間值函數的收斂定理.最后，討論了區間值Choquet 積分定義的集函數性質，結果表明，上下連續性、超可加、零可加、次可加、模糊可乘性等性質在其不定積分中均可遺傳到其原函數中.

1 定義及說明

2 區間值Choquet 積分及其性質

引理1 設(X，A，μ)是非可加測度空間，若f(x)，g(x)是非負可測的實值函數，則

(1)(c)∫max{f(x)，g(x)}dμ ≥max{(c)∫f(x)dμ，(c)∫g(x)dμ};

(2)(c)∫min{f(x)，g(x)}dμ ≤min{(c)∫f(x)dμ，(c)∫g(x)dμ}.

證明 只證(1)式.若(c)∫fdμ = + ∞或(c)∫gdμ = + ∞時(不妨設(c)∫fdμ = + ∞)，易知max{(c)∫f(x)dμ，(c)∫g(x)dμ}= + ∞;因為max{f(x)，g(x)}≥f(x)，由Choquet 積分的單調性知:(c)∫max{f(x)，g(x)}dμ ≥(c)∫f(x)dμ，結論得證.

若f(x)和g(x)都Choquet 可積的，即(c)∫fdμ ＜+∞且(c)∫gdμ ＜+∞，因為max{f(x)，g(x)}≥f(x)，所以(c)∫max{f(x)，g(x)}dμ ≥(c)∫f(x)dμ，同理可得(c)∫max{f(x)，g(x)}dμ ≥(c)∫g(x)dμ，結論得證.

定理2 令F，G ∈U［X，I(R+)］，若F，G 是c 可積的，則

(1)(c)∫(F ∨G)dμ ≥(c)∫Fdμ ∨(c)∫Gdμ;

(2)(c)∫(F ∧G)dμ ≤(c)∫Fdμ ∧(c)∫Gdμ.

證明 只證(1)式.由(F ∨G)(x)= ［F-(x)∨G-(x)，F+(x)∨G+(x)］，知

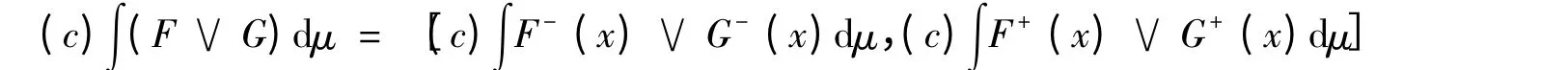
由定理1 知

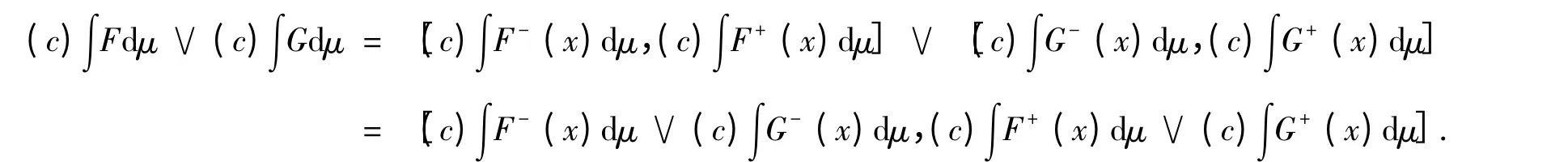
由引理1 知

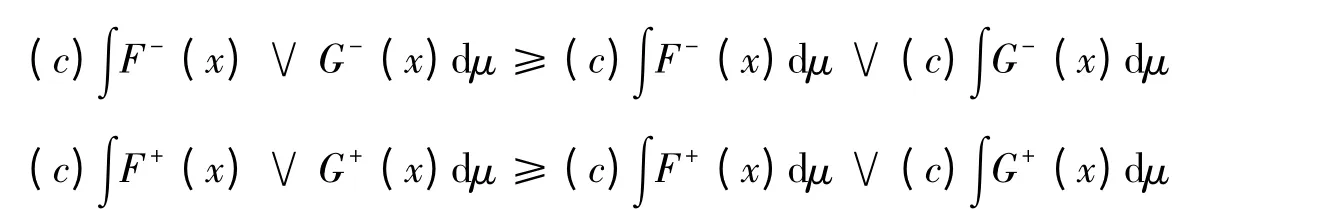
結論得證.

3 區間值Choquet 積分收斂定理

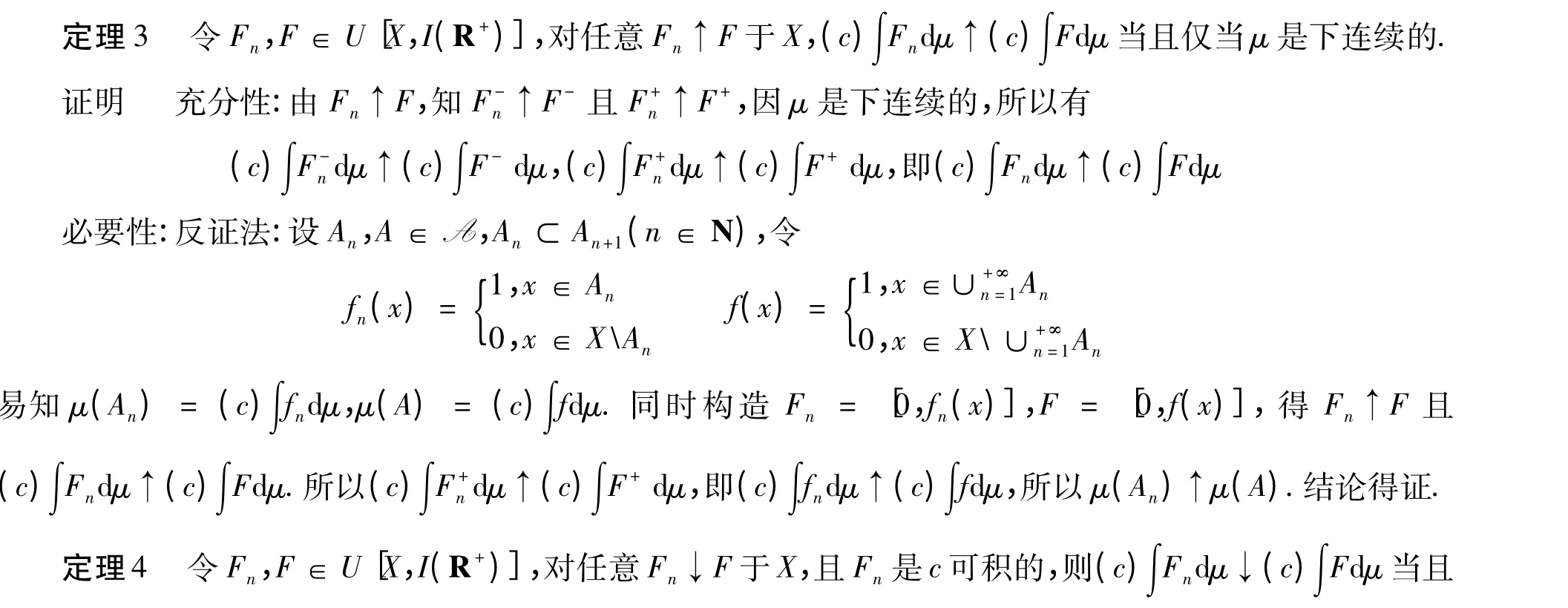
4 區間值Choquet 積分定義的集函數

注［8］:集值模糊測度是(下連續、上連續、連續)區間值模糊測度，當且僅當π-，π+是(下連續、上連續、連續)模糊測度(π-= inf π，π+= sup π).

例1 假設(X，F)是可測空間.令F ∈U［X，I(R+)］，記π(A)= (c)∫AFdμ，由性質1 易知π(A)是區間值模糊測度.

定理6 (1)若μ 是上連續的，則π(A)是上連續的;

(2)若μ 是下連續的，則π(A)是下連續的.

證明 只證明(2)式.設A1?A2?…?An?…，由定義3 和μ 是下連續性得

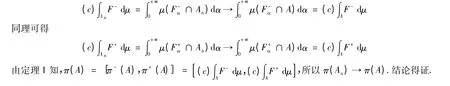
定理7

(1)若μ 是超可加的，則π(A)是超可加的;

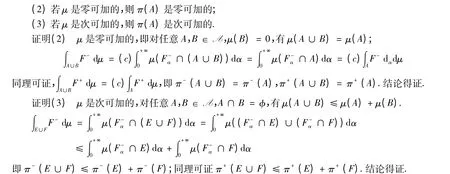
定理8

(1)若μ 是下自連續的，則π 也是下自連續的;

(2)若μ 是上自連續的，且F 是c 可積的，則π 也是上自連續的;

(3)若μ 是一致自連續的，且F 是c 可積的，則π 也是一致自連續的.

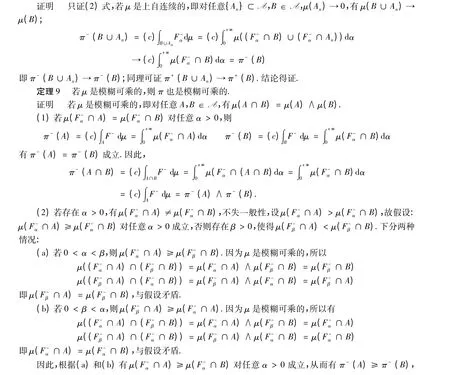
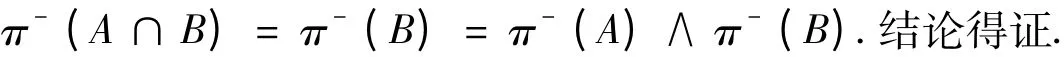
5 結論

根據集值積分經典定義方法，本文給出了較特殊的區間值函數關于經典測度的Choquet 積分的定義，并證明了其積分結果也是區間值的.同時，研究了單調集值函數的收斂定理，得到了若充要條件，需要指出若集值函數取成sup F(x)，inf F(x)上述結論將退化成經典的Choquet 積分;討論了區間值Choquet 積分定義的集函數關于的遺傳性質和結構特性，結果表明，諸如上、下連續性、零可加、超可加、模糊可乘等性質均可遺傳到原函數中.