基于子結構模型的平置式浮筏隔振系統功率流傳遞特性分析

門麗潔，余桐奎，龍 軍，劉文帥，王志偉，時勝國

（1.大連測控技術研究所，遼寧 大連116013；2.哈爾濱工程大學 水聲工程學院，哈爾濱150001）

對大型機械結構進行計算機建模仿真是研究其結構振動性能的一種常用手段。常用的機械結構系統建模方法主要包括：多剛度法、有限元法[1]、四端參數法[2-4]、機械阻抗綜合法[5-6]、模態阻抗綜合法、傳遞波法、動力縮聚法、頻響函數綜合法等，對于隔振系統的建模問題，目前應用比較多的是有限元法、機械阻抗綜合法、模態阻抗綜合法。

機械阻抗綜合法簡稱為阻抗綜合法，一些文獻稱之為導納綜合法、子結構導納綜合法。該方法是一種分析組合結構動力特性的實用手段，它是動態子結構方法的一種特殊形式。機械阻抗綜合法的基本思想是：先將整個系統或結構有目的地分解成若干個子系統或子結構，通過機械阻抗方法的理論計算或試驗測定，分別建立每個子結構的運動方程，再根據子結構間相互聯接的實際狀況，確定聯接面的約束條件，最后通過子結構之間的約束方程，將各個子結構的運動方程耦合起來，得到整個結構系統的運動方程和動力特性。

近年來國內外學者逐漸開展了對結構振動功率流的研究[9-13]。國內牛軍川等[7]采用子結構導納綜合法和傳遞矩陣技術,建立了多激勵多支承的全柔性隔振系統動力學模型，給出適合于不同隔振系統的傳遞率和功率流表達式。肖斌[8]通過建立子系統傳遞矩陣，利用功率流法實現被動隔振過程振動傳遞特性研究，分析了隔振系統主導模態、耦合和阻尼等耗散特征以及初級激擾力特征對各振動通道能量分布和傳遞特性的影響。這些研究從能量角度對隔振系統的設計給出了更有效的分析評價方法。

浮筏隔振系統主要由激勵源設備、上下層隔振器和浮筏筏架組成，改變系統各組成部分的結構參數對浮筏隔振效果都會產生不同的影響，通過改變這些結構參數可有效改善整個系統的隔振性能，但改變哪些組件的結構參數會更有效呢？本文基于振動功率流分析，采用子結構導納法和四端參數法，通過建立基于彈性基礎的多激勵多自由度平置式浮筏隔振系統的動力學模型，推導出隔振系統中傳入整個系統和傳入各子系統的功率流與激勵力之間的數學表達式，分析不同結構參數條件下振動能量傳遞特性的變換規律。參考船用浮筏隔振裝置實際參數，建立了三源激勵平置式浮筏隔振系統的數值模型。通過對浮筏隔振系統模型中隔振器、機組、筏體及基礎的結構參數進行數值仿真分析，給出了平置式浮筏各子結構參數變化引起的傳入基礎及其他子系統功率流的變化規律和相對量級。

1 平置式浮筏隔振系統動力學模型

1.1 平置式浮筏隔振系統動力學模型

平置式廣義浮筏結構的動力學模型如圖1所示。在實際工程應用時，機組和浮筏筏架的安裝頻率一般都會遠低于主機擾動頻率，且浮筏本身的剛性很大，因此將浮筏機組設備和浮筏均簡化為剛體，基礎板簡化為四邊簡支薄板，整個結構關于xoz平面對稱。系統由s臺設備組成，第k臺設備由pk個隔振器支撐，上層隔振器共有n個，下層隔振器共有m個。

系統分為機組設備、上層隔振器、筏架、下層隔振器和基礎共5個子系統。各子系統之間的動態傳遞關系如圖2所示。定義速度正方向始終向下，每個子系統的正方向為指向各自子系統，剛體轉動速度以逆時針為正向。

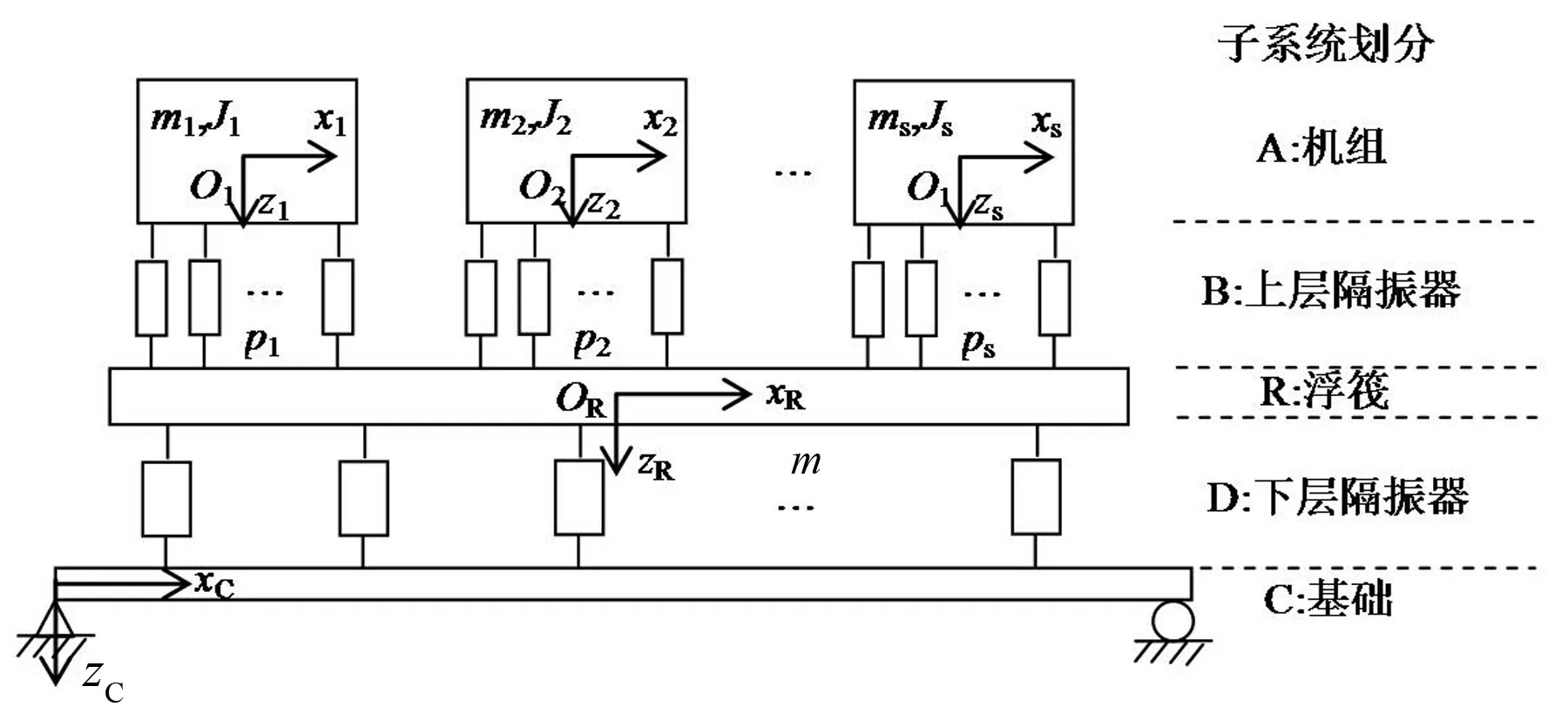
圖1 平置式浮筏隔振系統動力學模型示意圖

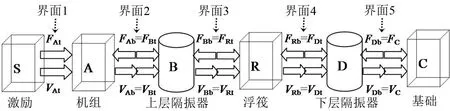
圖2 浮筏隔振系統中各子系統的動態傳遞關系圖

1.2 子系統導納分析

對于機組子系統，根據剛體動力學理論，第k臺設備的動力學平衡方程如下：

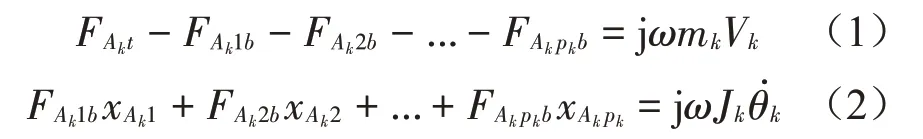
式中：mk、Jk分別為第k臺設備的質量、轉動慣量和角速度，基于剛體設備假設，與同一臺設備連接的不同隔振器連接處的角速度應相等。

第k臺設備的第lk個隔振器上端運動速度為

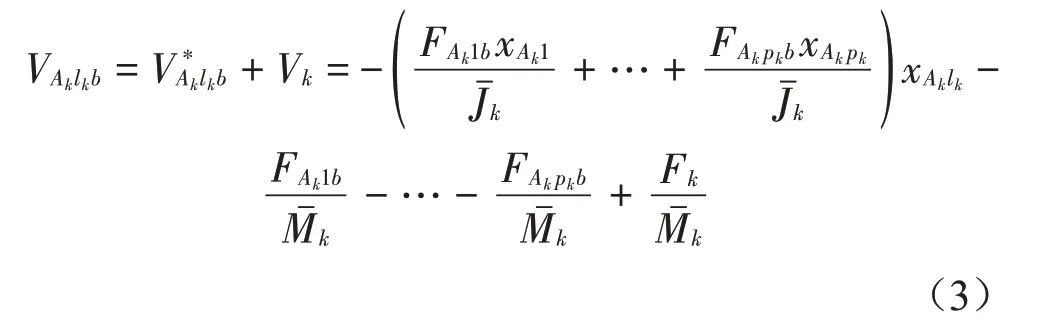
將各臺設備的動力學方程寫成導納方程形式有：

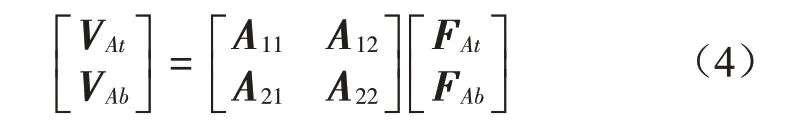
式中：VAt和FAt分別為機組A的耦合界面力和速度向量，VAb和FAb為上層隔振器陣列B的耦合界面力和速度向量。式中導納矩陣

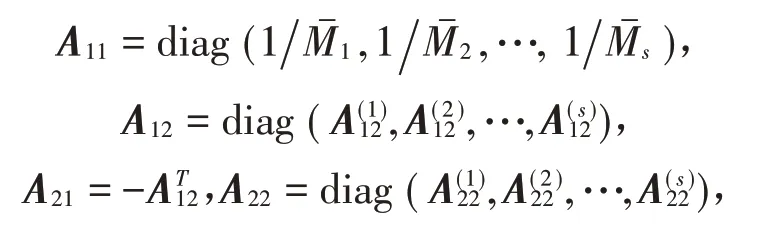
其中：

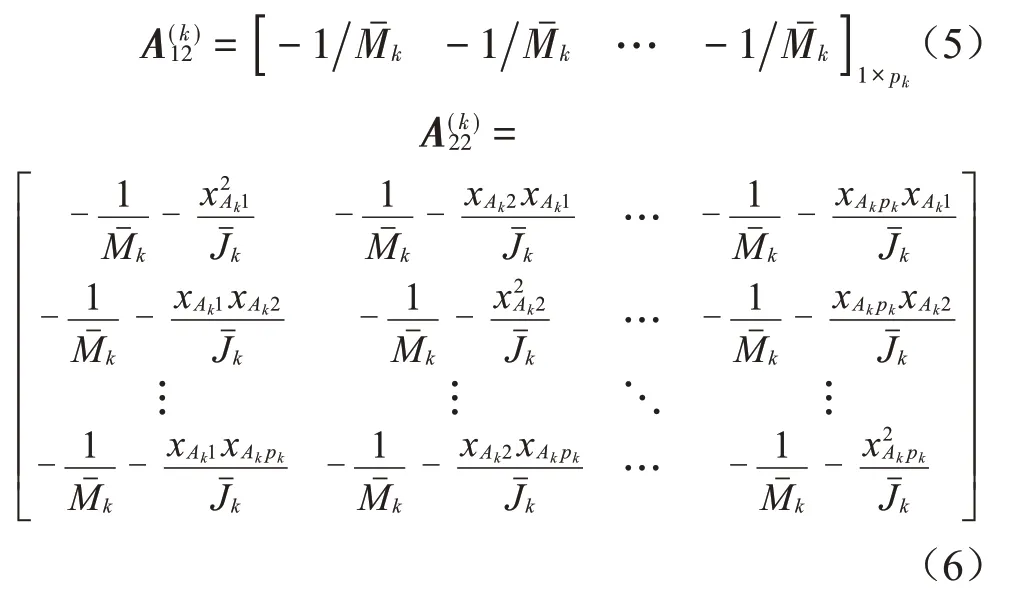
對于上層和下層隔振器子系統，忽略隔振器質量，隔振器假設為一對大小相等、方向相反的力。上下層隔振器的復剛度矩陣可寫為KB=diag(k*B1,k*B2,…,k*Bn)和KD=diag(k*D1,k*D2,…,k*Dm)。式中：k*Bk=kBk(1+jηBk)和k*Dl=kDl(1+jηDl)分別表示第k個上層隔振器和第l個下層隔振器的復剛度，其中ηBk和ηDl分別表示第k個上層隔振器和第l個下層隔振器的阻尼損耗因子。

上層和下層隔振器的動態方程如下：

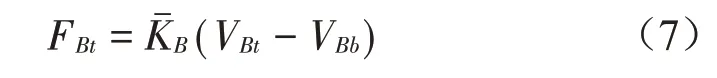
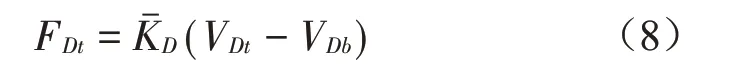
由于很難獲得四邊自由薄板精確解，對浮筏筏體子系統進行導納分析有較大難度，采用剛體來模擬筏體。剛體浮筏的動力平衡方程為

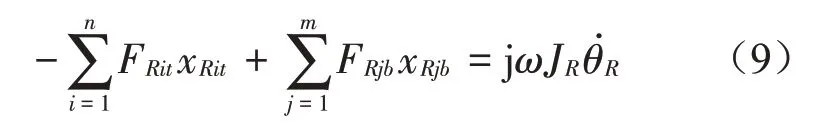
式中：JR表示筏體的轉動慣量和角速度，與浮筏連接的不同隔振器連接處的角速度應相等。

剛性浮筏的導納方程為

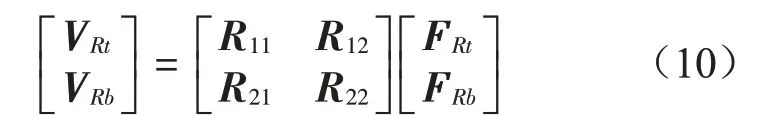
式中：FRt和VRt表示浮筏子系統上端的輸入力和速度向量，FRb，VRb表示下端輸入力和速度向量，并有，R12=-RT21。

對于基礎子系統，采用四邊簡支矩形板來模擬彈性基礎板，與彈性浮筏的微分方程和求解形式相同。可求得簡諧激勵Fc在點σ(x0,y0)作用時板在任意一點處的速度響應為

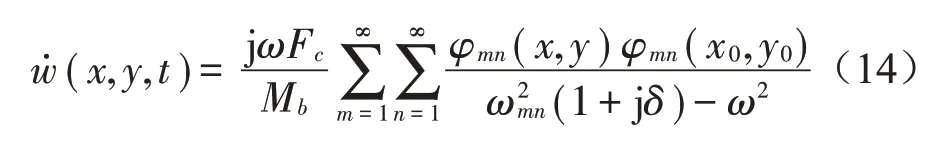
可以得到，在任意點σ(xi,yi)激勵時，任意點σ(xj,yj)的導納函數為[6-8]

式中：Mb為板的模態質量，Mb=ρhlxly/4，ρ、h分別為板的密度和厚度，lx、ly為基礎板的長和寬，δ為損耗因子。四邊自由簡支薄板的振型函數為

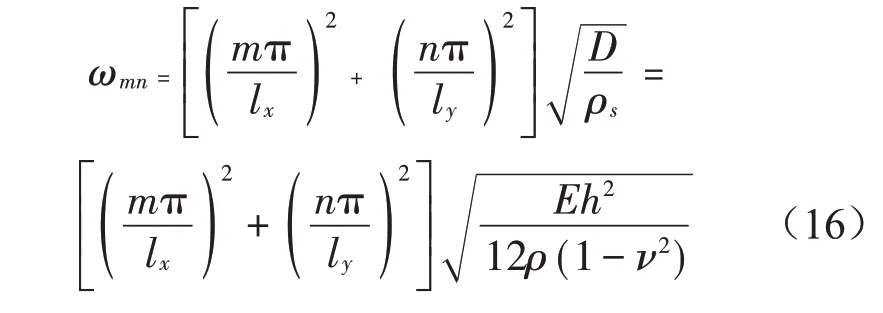
其為四邊簡支板矩形薄板的固有頻率，其中，D=Eh3/12(1-ν2)，ρs為矩形板的面密度，E、ν分別為材料的楊氏模量和泊松比。裝有m個隔振器的基礎板子系統導納矩陣方程為

式中，導納矩陣C為m×m方陣，方陣中的元素為Cij。

1.3 動力學傳遞方程

浮筏系統中各子系統之間的動力傳遞關系如圖2所示。由式（4）、式（7）、式（8）、式（10）、式（17）可求得浮筏系統中各子系統耦合界面力和速度響應。得到激勵源耦合界面1處的速度響應為

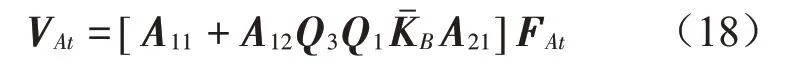
機組與上層隔振器耦合界面2處的力和速度為

上層隔振器與浮筏上表面耦合界面3處的力和速度為

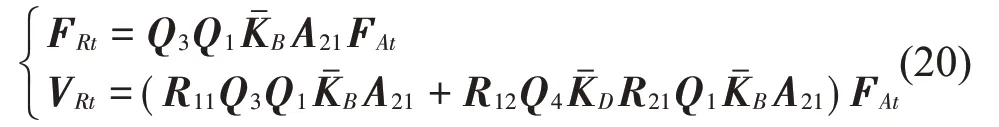
浮筏下表面與下層隔振器耦合界面4處的力和速度為

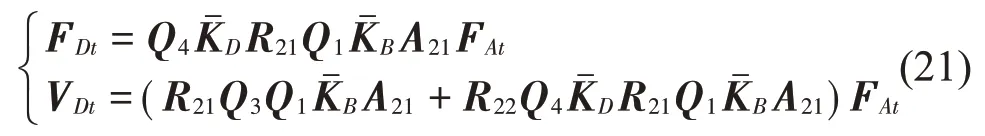
下層隔振器與基礎耦合界面5處的力和速度為

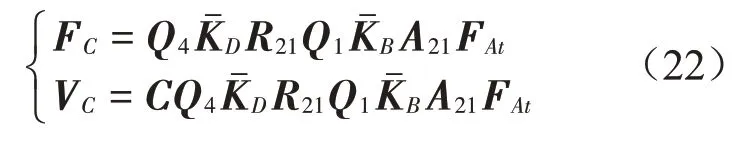
其中：

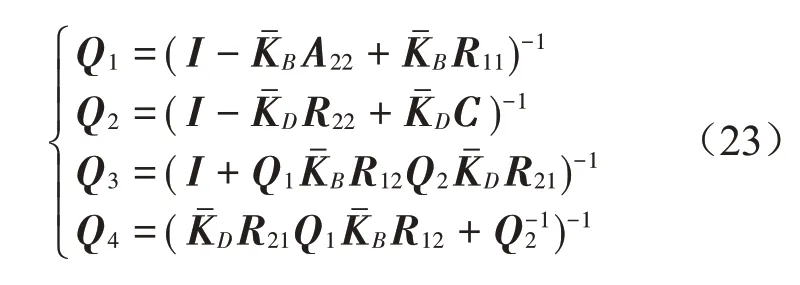
2 系統功率流表達式

振動功率流是功率概念在振動分析領域的延伸，指單位時間內振動的能量。假設作用于某點處的外力為F(t)，該點處的速度為V(t)，則由該點輸入結構的瞬時功率為

通常使用一段時間內的平均功率來反映外部注入結構的能量強度，并且把按時間平均的振動功率稱為振動功率流，即：

對于實際的振動問題，振動信號往往可以用疊加后的簡諧信號來表示。因此可以設激勵力為F=Fejωt，那么響應速度可寫為V=Vejωt，則有

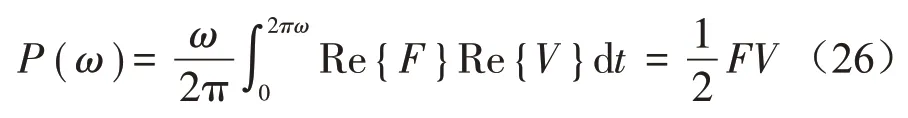
上式可寫為

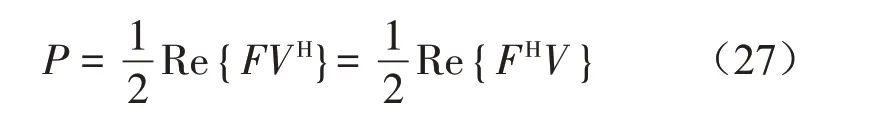
3 平置式浮筏隔振系統參數模型

參考船用機械系統及浮筏結構參數，建立平置式浮筏隔振系統參數模型，如圖3所示。考慮到模型的一般性，假設隔振系統的機組中有3臺激勵設備，其中2臺（1號、2號）是同型設備，并且3臺設備的安裝位置關于x軸方向對稱，具體安裝位置和尺寸見俯視圖。

機組設備：1、2號泵的質量均為1 000 kg，設備尺寸（Lx×Ly×Lz）均為1 000 mm×700 mm×400 mm；3號泵的質量為2 000 kg，尺寸為1 000 mm×1 500 mm×400 mm。

筏體：尺寸為3 500 mm×2 000 mm×80 mm，材料密度為7 850 kg/m3，則質量為4 396 kg。

基礎板：尺寸4 000 mm×2 500 mm×15 mm，材料密度為7 850 kg/m3，則質量為1 471.875 kg。材料彈性模量E=2.1×1011Pa，泊松比為0.29，阻尼因子δ=0.01。采用參考船用E型系列隔振器，上層隔振器選用E-15，Z向動剛度為450 N/mm，下層隔振器選用E-220，Z向動剛度為7 000 N/mm。

4 數值仿真

4.1 隔振器參數對功率流傳遞的影響

利用子結構導納法和四端參數法建立平置式浮筏隔振系統動力學模型，通過改變上下層隔振器的剛度和阻尼，仿真分析隔振器參數變化對傳入整個系統和各子系統功率流的影響。

上層隔振器剛度對傳入各子結構的功率流均有較大影響。如圖4所示。

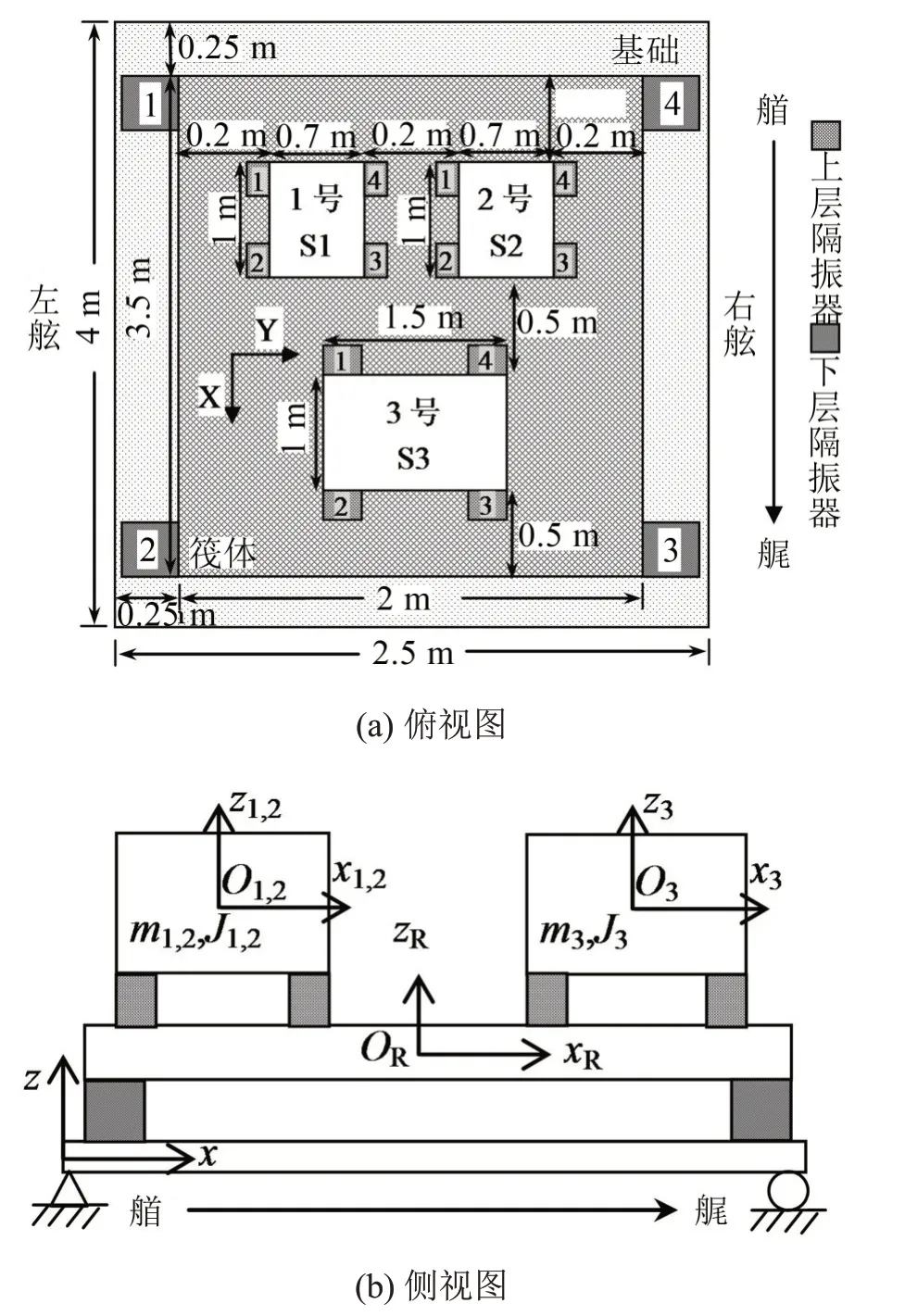
圖3 平置式浮筏隔振系統參數模型圖

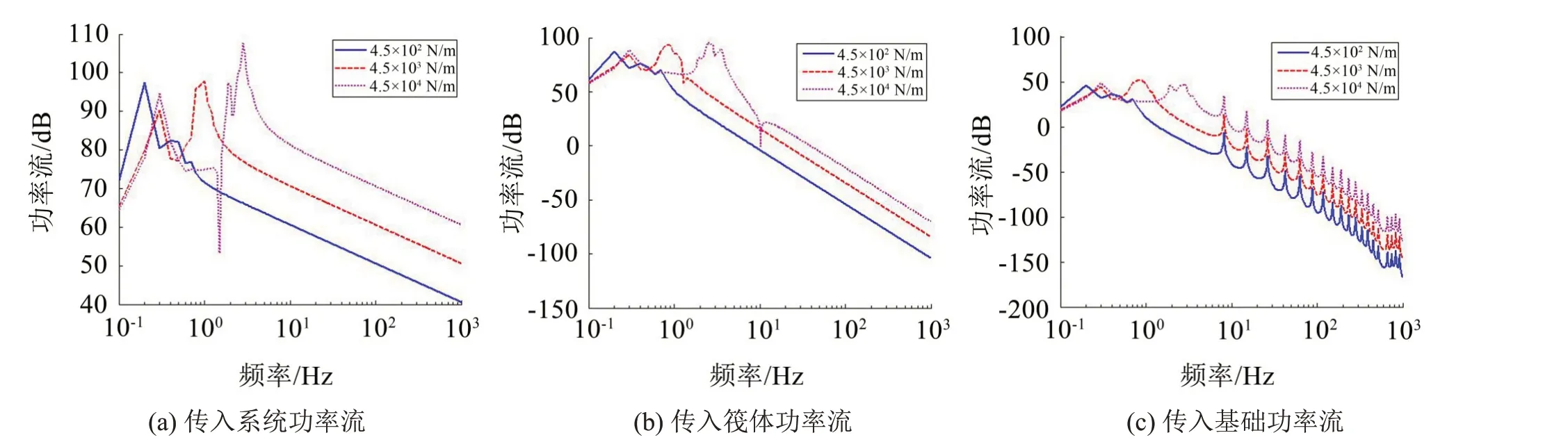
圖4 上層隔振器剛度變化對傳入子結構功率流的影響

圖5 上層隔振器阻尼變化對傳入子結構功率流的影響

上層隔振器的剛度越小，系統的剛性模態頻率越低，同時傳入整個系統及傳入筏體和基礎的功率流也越小。剛度每減小10倍，在剛體模態頻率以上頻段傳入整個系統和傳入基礎的功率流分別整體下降約10 dB和20 dB，而傳入筏體的功率流平均整體下降16 dB左右。

上層隔振器的阻尼變化主要對剛體模態頻率處的功率流大小產生一定影響，如圖5所示。阻尼因子每增大0.05，剛體模態頻率（0.2 Hz）處傳入各子系統功率流譜幅度均減小1 dB～2 dB；但對于傳入整個系統的功率流譜，剛體模態頻率以上頻段功率流譜幅度隨阻尼因子的增大略有增加，阻尼因子每增大0.05，功率流譜幅度增大2 dB～3 dB。

下層隔振器剛度對傳入筏體和基礎的功率流影響較大，而對傳入整個系統功率流的影響主要體現在剛體模態頻率隨剛度減小略有變化。如圖6所示，隨著剛度的減小，在傳入筏體和基礎的功率流譜上，隨頻率快速衰減的拐點頻率降低，隨頻率快速衰減的頻段增大；剛度每減小10倍，傳入筏體和基礎的功率流譜在剛體模態頻率以上頻段分別整體減小約10 dB和20 dB。

下層隔振器阻尼對傳入各子系統功率流具有一定影響，主要體現在剛體模態頻率附近。阻尼因子每增大0.05，傳入各子系統功率流在剛體模態頻率（0.2 Hz）處峰值均減小1 dB左右；但對于傳入筏體的功率流譜，在剛體模態受到抑制的同時，其它頻段的功率流譜幅度有1 dB～3 dB的增強。

4.2 機組參數對功率流傳遞的影響

通過改變機組相關參數，分別對不同的機組質量、機組轉動慣量和機組間距情況下傳遞的功率流進行分析，并對機組設備開啟數量對傳入各子系統功率流的影響進行分析。

保持機組質量的對稱性，使機組質量整體變化，即機組中每臺設備按相同比例變化。分別選取0.2倍、1倍和5倍機組質量進行仿真，如圖7所示。結果表明，機組質量整體每增大5倍，除系統的剛體模態頻率略有降低外，傳入整個系統、筏體及基礎的功率流均整體下降約14 dB。

分別取0.1倍、1倍和10倍機組轉動慣量時仿真結果表明，機組轉動慣量對稱或非對稱變化對傳入各子系統的功率流影響很小。而減小機組間距會使傳入筏體和基礎的功率流總和略有降低。關閉3臺設備中的1臺和2臺，傳入整個系統的功率流總和分別降低約2 dB和5 dB，傳入基礎的功率流總和分別降低約3 dB和9 dB。

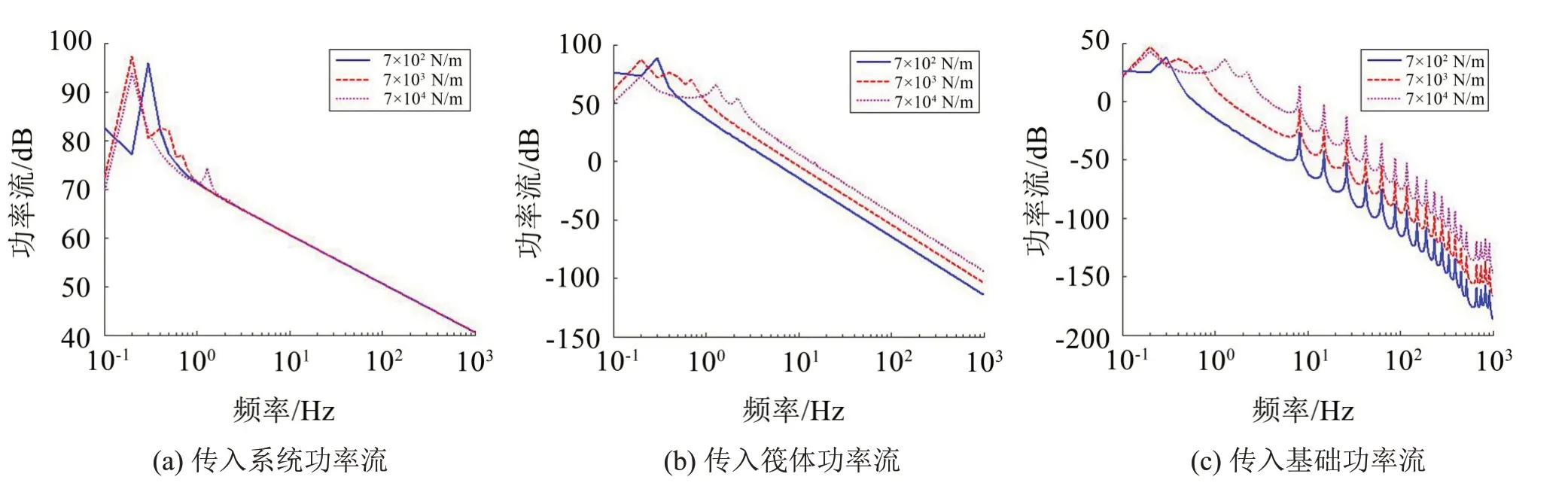
圖6 下層隔振器剛度變化對傳入子結構功率流的影響

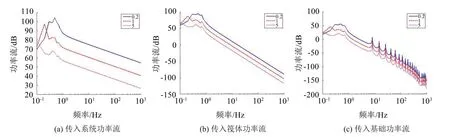
圖7 機組質量對稱變化對傳入子結構功率流的影響

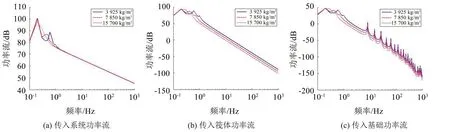
圖8 筏體質量對傳入各子系統功率流總和的影響

4.3 筏體參數對功率流傳遞的影響

在浮筏整體尺度不變的情況下，分析不同筏體質量（材料密度）對傳入各子系統功率流總和的影響。仿真結果如圖8所示。隨著筏體密度的增大，除剛體模態頻率略有降低外，傳入筏體和基礎的功率流總和幅度整體降低，密度每升高一倍功率流總和幅度整體降低約6 dB。

4.4 基礎板參數對功率流傳遞的影響

仿真結果表明，如圖9所示。在其他參數不變的情況下，改變基礎板的厚度對傳入基礎功率流的幅度和彈性模態頻率均有較大影響，在10 Hz以內的彈性模態以下頻段，厚度增大一倍其傳入基礎的功率流譜幅度就減小9 dB以上，同時隨著基礎板厚度的增加，各階彈性模態頻率均有所升高，各階彈性模態頻率的間隔有不同程度加大。基礎板長度和寬度的變化主要影響傳入基礎功率流譜的彈性模態頻率，長度或寬度的增加會使各階彈性模態的頻率降低，并使各階彈性模態頻率的頻率間隔減小。

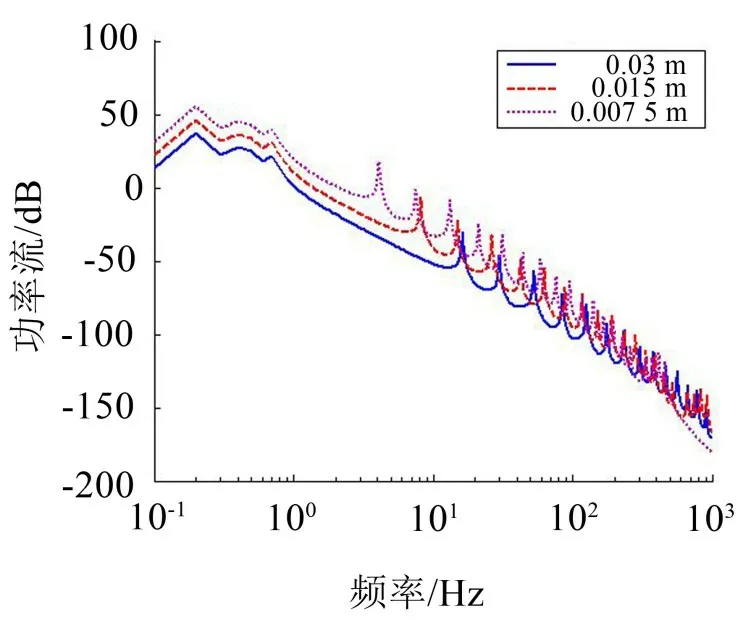
圖9 基礎板厚度變化對傳入基礎功率流的影響

5 結語

本文通過建立基于彈性基礎的多激勵多自由度平置式浮筏隔振系統的振動功率流傳遞的動力學模型，仿真分析了隔振系統結構參數對傳入基礎的功率流大小的影響。結果表明：

（1）浮筏系統中上層和下層隔振器剛度對傳入各子系統功率流的整體幅度影響最大，通過減小隔振器剛度，尤其是上層隔振器剛度，可使傳入基礎的功率流降低幾十分貝。

（2）浮筏系統中設備和筏體質量對傳入各子系統的功率流幅度有較大影響，在不破壞對稱性的前提下，增加機組設備或筏體的質量，將使傳入基礎的功率流下降幾分貝甚至十幾分貝。但設備和筏體質量選取受實際因素的限制，調整范圍有限。

（3）適當增大基礎板的厚度可以使傳入基礎的功率流幅度下降幾分貝，并使模態頻率在升高的同時變稀疏；

（4）設備開啟數量、隔振器間距、設備間距等參數及安裝的對稱性也對傳入基礎的功率流有一定影響。