基于目標的相機標定方法
王利華 李亮亮 郭恒林
(山東科技大學(xué) 測繪科學(xué)與工程學(xué)院, 山東 青島 266590)
0 引言
隨著計算機視覺和數(shù)字攝影測量的發(fā)展,基于視覺的坐標測量技術(shù)得到了更廣泛地應(yīng)用。相機的內(nèi)參和光學(xué)畸變系數(shù)被用于描述相機自身特性,是精確獲取被測物體的三維坐標的前提。通過一定的方法和手段獲取相機內(nèi)參和光學(xué)畸變系數(shù)的過程就是相機標定。
相機標定方法根據(jù)標定方式的不同,主要可以分為兩種:自標定方法和基于目標的標定方法[1]。自標定方法存在約束性較差[2]、對噪聲敏感等缺點[3-4]。因此,基于目標的相機標定方法,仍具有重要的作用。基于目標的相機標定方法是指用一個結(jié)構(gòu)已知、精度很高的標定物或控制場作為空間參照物,通過空間點和影像點之間的對應(yīng)關(guān)系來建立相機參數(shù)約束,然后通過優(yōu)化算法來求取這些參數(shù)[5]。基于目標的相機標定方法主要包括計算機視覺中的張正友標定法和攝影測量中基于直接線性變換(Direct Linear Transformation, DLT)、空間后方交會的標定法。張飛[6]和靳沖[7]等主要針對計算機視覺中的相機標定方法做了比較與分析,王冬[8]主要對攝影測量中相機標定做了研究與分析。本文針對上述3種方法進行了研究分析。
1 基于目標的相機標定方法原理
1.1 后方交會標定法原理
由攝影測量中的共線方程出發(fā),再根據(jù)空間后方交會原理并考慮光學(xué)畸變,可以得到空間后方交會相機標定的誤差方程:
V=AXe+BXi+CXd-L
(1)
式中,Xe是外方位元素;Xi是內(nèi)方位元素;Xd是畸變系數(shù);A、B、C為對應(yīng)的系數(shù)矩陣;L是系數(shù)矩陣。利用物點坐標和對應(yīng)的像點坐標迭代求解,可以得到需要標定的參數(shù)。
1.2 直接線性變換標定法原理
根據(jù)攝影測量中的共線方程,考慮到光學(xué)畸變,可以導(dǎo)出多余觀測下直接線性變換的基本關(guān)系式:
(2)
式中,(x,y)是像點坐標;(vx,vy)是像點坐標對應(yīng)的誤差值;(Δx,Δy)為光學(xué)畸變;(X,Y,Z)是像點對應(yīng)的物方坐標;li是關(guān)于內(nèi)外方位元素的函數(shù)。
先利用直接線性變換的直接解法求取初值再利間接平差進行迭代求解即可求取li和畸變系數(shù),再根據(jù)等式(3)即可求得相機內(nèi)參。
(3)
1.3 張正友標定法原理
張正友標定法[9]從計算機視覺中的相機模型出發(fā),結(jié)合相機的單應(yīng)性矩陣并利用標定板作為控制場求解相機的畸變系數(shù)和內(nèi)部參數(shù)。
設(shè)光學(xué)相機模型為:
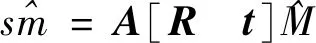
(4)
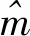
則有:
[h1h2h3]=λA[r1r2t]
(5)
根據(jù)旋轉(zhuǎn)矩陣的正交性有:
(6)
根據(jù)單應(yīng)性矩陣H再利用等式(6)可以求取內(nèi)外參數(shù)的初值,再計算畸變系數(shù)。
2 實驗設(shè)計與結(jié)果分析
2.1 實驗設(shè)計
3種相機標定方法對控制場的要求不同,其中空間后方交會和直接線性變換都是基于三維控制場,而張正友標定法采用二維控制場。對于三維控制場選擇山東科技大學(xué)高精度相機標定場,二維控制場選擇高精度的標定板。本次實驗所采用的相機為Canon200D,此相機為非量測型相機,其分辨率為6 000×4 000個像素,傳感器尺寸為22.3 mm×14.9 mm,鏡頭型號為:Canon EF-S 18-55 mm f/4-5.6 IS STM。
2.1.1 空間后方交會和直接線性變換標定法實驗設(shè)計
基于空間后方交會和直接線性變換的相機標定方法都需要精確的三維空間坐標。本次實驗采用徠卡TM5100A經(jīng)緯儀工業(yè)測量系統(tǒng),其測角精度為0.5″。通過該測量系統(tǒng)對三維控制場的394個控制點進行精確測量,同時采用Canon200D相機對控制場拍攝3~5張像片,從中選擇成像質(zhì)量最好的單張像片作為實驗照片。
2.1.2張正友標定法實驗設(shè)計
在張正友標定法中根據(jù)標定板的設(shè)計值,選取其角點作為二維控制點。本次實驗采用8×8的標定板,其單元網(wǎng)格大小為75 mm×75 mm。將該標定板固定在平面上,利用Canon200D相機從各個方向?qū)硕ò暹M行拍攝,像片數(shù)量在20~30張,以達到最佳標定效果[10]。
2.1.3程序設(shè)計
本文針對3種不同的標定方法,根據(jù)上述理論介紹并結(jié)合實際使用需要,在VC++環(huán)境下對空間后方交會和直接線性變換方法進行實現(xiàn),對于張正友標定法采用MATLAB相機標定工具箱進行實驗。
2.2 三種相機標定方法的結(jié)果分析
2.2.1空間后方交會標定結(jié)果比較分析
將鏡頭分別設(shè)置為18、35、55 mm 3種不同的焦距進行像片數(shù)據(jù)采集,隨機選取20個控制點,利用空間后方交會程序?qū)ο鄼C參數(shù)進行計算。對于徑向畸變和切向畸變,其高階改正分量不但不能提高精度,反而引起解的不穩(wěn)定性[11],這里只取前2項。同時,為了比較不同焦距下的鏡頭畸變情況,選取像點A,令其像素坐標為(500,500), 利用標定結(jié)果中的畸變系數(shù)計算A點坐標畸變改正值(Δx,Δy),結(jié)果如表1所示。由表1可以發(fā)現(xiàn),隨著焦距的增大,畸變改正值的絕對值總體呈現(xiàn)先減小后增大的趨勢。在使用常規(guī)鏡頭時,為了保證鏡頭畸變比較小,應(yīng)當適當選擇焦距大小。

表1 不同焦距的空間后交標定結(jié)果
將焦距固定在18 mm附近,隨機選擇數(shù)量不同的控制點,其空間后方交會標定結(jié)果及中誤差如表2所示。由表2可以發(fā)現(xiàn):隨著控制點數(shù)量的增加,相機內(nèi)方位元素和畸變系數(shù)并沒有明顯的變化,說明如果隨機選擇10個控制點,其解算結(jié)果已經(jīng)比較可靠。但是參數(shù)之間往往具有相關(guān)性[12-13],為了避免解的強相關(guān)性,可以選擇多于10個點。其次,隨著控制點數(shù)量的增加其解算精度并沒有提高。這主要受到像片中控制點坐標精度的影響。在三維控制場中,所有點的成像質(zhì)量不可能完全一致,特別是在景深較大的時候,很難保證邊緣控制點的成像質(zhì)量。因此,在利用空間后方交會進行相機標定時,控制點應(yīng)盡量隨機分布,且控制點數(shù)量不宜過多。
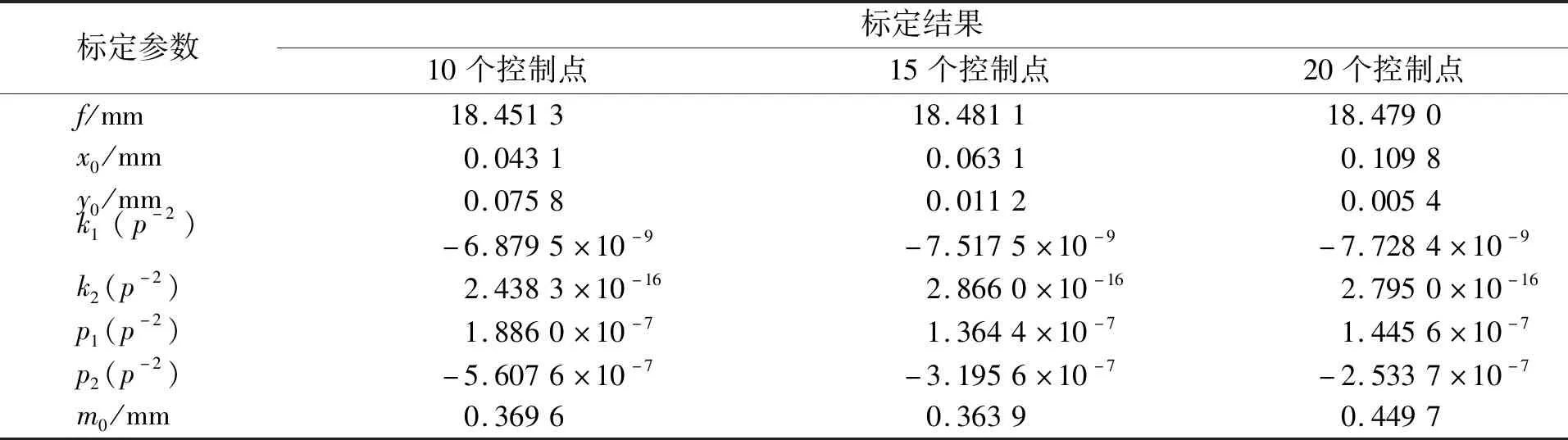
表2 不同控制點數(shù)量的空間后方交會標定結(jié)果
2.2.2 直接線性變換與空間后方交會標定結(jié)果比較分析
對于直接線性變換和空間后方交會,分別設(shè)置18、35、55 mm焦距,并分別選取同一組像片上的相同控制點,利用多組數(shù)量不同的控制點進行實驗,焦距大小、控制點數(shù)量、標定參數(shù)單位權(quán)中誤差之間的關(guān)系如圖1所示。
根據(jù)表2得到的結(jié)論可知,控制點的選取不宜過多。由圖1可以發(fā)現(xiàn):在控制點數(shù)量為15的情況下,直接線性變換的標定精度總體上優(yōu)于空間后方交會的標定精度。

圖1 焦距大小、控制點數(shù)量與精度的關(guān)系
此外,隨著焦距的增大,無論是直接線性變換還是空間后方交會,其標定精度基本都有所降低。這是由于隨著焦距的增大,景深逐漸變小,同時視場角也有所減小,前者會嚴重影響像片中控制點標志的成像質(zhì)量,后者會影響控制點的數(shù)量和分布。因此,在焦距增大時,直接線性變換和空間后方交會標定方法均存在一定程度上精度下降的問題。
2.2.33種標定方法標定結(jié)果比較分析
將相機焦距固定在18 mm附近,利用3種方法分別進行相機標定。其結(jié)果如表3所示。
由表3的結(jié)果可以發(fā)現(xiàn):在內(nèi)方位元素上,張正友標定方法結(jié)果略大于其余兩種方法的結(jié)果,就精度而言,張正友標定法的精度低于其他2種方法。

表3 3種方法標定結(jié)果
3 結(jié)束語
本文針對基于目標的相機標定3種常用的方法:攝影測量中的空間后方交會和直接線性變換標定法、計算機視覺中的張正友標定法,介紹其相關(guān)理論,并通過實驗數(shù)據(jù)分析了3種方法在焦距、控制點數(shù)量、精度方面的特點。可以得出如下結(jié)論:
(1)對于空間后方交會標定方法而言,控制點應(yīng)盡可能隨機分布且控制點數(shù)量在15個左右為宜,過多的控制點反而會使得精度下降。
(2)隨著焦距的增加,直接線性變換和空間后方交會標定精度均有所降低。
(3)直接線性變換標定方法、空間后方交會標定方法、張正友標定方法的標定精度依次降低。
(4)張正友標定法具有很好的便捷性,但影響精度的因素很多,穩(wěn)健性不如其他2種方法。直接線性變換標定方法無須初值,而空間后方交會則需要設(shè)置合理的初值,若初值不合理,可能會導(dǎo)致解算結(jié)果錯誤甚至無法解算出結(jié)果。

