論數學學習中的“卡點”及解決策略

李宏貞

數學教學中存在這樣的情況，學生沒有理解某個知識點，并不是態度問題，也不是教師講解不深刻的問題，而是學生在理解這個知識的過程中在某個點上“卡”住了。這個點是學生在某個具體知識上理解的障礙點，解決了這個“攔路虎”，問題就迎刃而解。不少教師忽視了學生的卡點問題，往往把學生對知識的不理解歸結于學習態度問題，忽視了學生真正需要幫助的卡點問題，沒有真正去了解學生“卡”住的原因，沒有因人施策，導致學生掌握不了這個知識。筆者對某小學四年級全體學生進行了一個學期的研究，通過輔導學生解決錯題的方式進行觀察和反思，將學習中的卡點歸納為三類并提出解決策略。

一、陳述性卡點

陳述性卡點就是由于學生陳述性知識缺乏所造成的對某個知識點的理解障礙。所謂陳述性知識就是“是什么”的知識，指的是一般的事實、原理等知識，陳述性知識大致上與傳統的知識概念相當。陳述性卡點是最普遍的卡點，學生學習數學因為陳述性知識的缺乏，往往導致錯題的發生。

題目：一個三角形的兩個內角分別是84°和48°，它的第三個角是（??），這是一個（??）三角形。

這是一道比較容易解答的題目，只要掌握了三角形兩個基本的陳述性知識“三角形的內角和為180°”“銳角三角形是三個角都小于90°的三角形”，問題就可迎刃而解。但恰恰有些學生沒記住這兩個陳述性知識。第一個陳述性知識“三角形的內角和為180°”是四年級下學期新學的知識，有些學生雖然課堂上掌握了，但課后遺忘了;第二個陳述性知識是四年級上學期的知識，由于學習間隔時間太長，學生也忘記了。而教師往往忽視陳述性知識容易遺忘的特點，對第一個知識，認為經過課堂上對內角和為180°的推理分析和動手實踐，學生肯定能掌握，即使不理解，也能記住，沒有針對性地對這個新學的知識作必要的強化訓練;對第二個知識，沒有意識到需要進行復習，加強與新知識的聯系。

解決陳述性卡點的課堂教學策略是強化策略和先行組織者策略。根據遺忘曲線規律，遺忘的進程很快，并且先快后慢。根據這個定律，學習要經常復習，不定時復習。教師對于新知識，特別是核心知識，需要在課堂上及時強化，課后不定時復習。

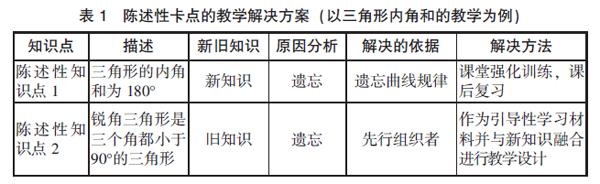
所謂的先行組織者，是指在學習新知識之前，為學生呈現一個引導性材料，這個材料有助于學生對新知識的理解。教師在講解三角形內角和之前，可以讓學生復述鈍角三角形、直角三角形和銳角三角形三者之間的聯系與區別，作為學習三角形的引導性材料，然后分小組探究這三類三角形內角和的規律，再歸納出三角形內角和為180°這一知識點。解決陳述性卡點的教學策略見表1。

二、程序性卡點

程序性卡點就是由于學生程序性知識缺乏所造成的對某個知識點的理解障礙。所謂程序性知識是“如何做”的知識，通常以一系列要遵循的步驟的形式出現。它包括技能、算法、技術和方法的知識，還包括用于決定何時運用不同程序的標準的知識。簡單來說，程序性知識就是“怎么做”的知識。造成學生學習出現卡點的第二類原因是程序性知識缺乏，下例就屬于這種情況。

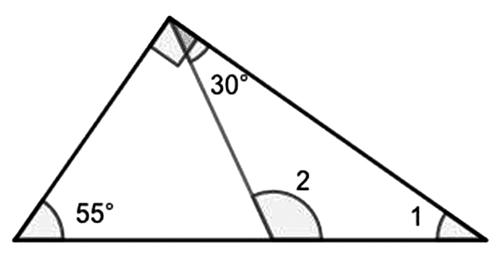
例：如圖1，求出：∠1=（???），∠2=（???）。

以∠1的求解為例，這個問題的卡點就是程序性卡點，學生雖然知道三角形的內角和為180°，也知道直角三角形的兩個銳角和為90°，但就是不知道如何求∠1，或者沒能意識到可以通過三角形三個內角之間的關系來求∠1，這就是程序性知識缺乏造成的卡點。解決這道題的程序性知識為：（1）識別出∠1處在直角三角形中。（2）識別出圖中的55°角和∠1同處于同一個直角三角形中，它們的和為90°。（3）用90°減去55°得出∠1的數值。解決程序性知識缺乏造成的程序性卡點，需要學生掌握條理化解決問題的程序并實現深度的理解。

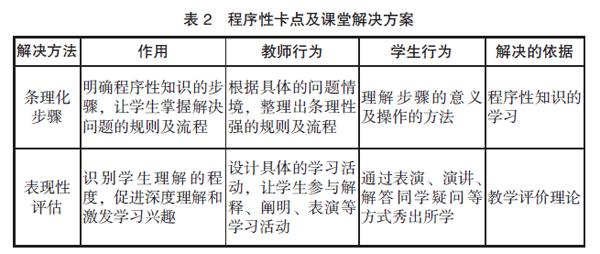
小學的數學問題，一般是結構良好的問題，結構良好的問題就是有明確的問題條件和標準化的解決方案。教師需要把解決問題的過程進行梳理，以幫助學生理順邏輯思維，把解決問題的步驟條理化，讓學生容易理解，習得解決問題的規則，并通過課堂練習，用這些規則解決問題。通過訓練，規則變成了技能，也就解決了程序性卡點，掌握了解決此類問題的專門領域的程序性知識。學生課堂上的理解往往是淺層次的理解，規則和技能會隨著時間迅速遺忘或者退化，為了實現深度的理解以及讓程序性知識進入長時記憶，除了當堂的強化練習外，課堂上的表現性評估活動也很重要。所謂的表現性評估就是通過學生的表現（解釋、闡明、表演等）實現對學生是否理解及理解程度的判斷。通過表現性評估，能夠使學生在加強對知識理解的同時加強選擇性記憶，促進知識從工作記憶進入長時記憶，是從學生的角度解決程序性知識缺乏、激發學生學習興趣的良好方法。課堂語言設計上，簡單來說，就是如下的對話：“這個解題步驟你懂了嗎？”“懂了。”“那好，講給教師（同桌、小組成員）聽。”教學設計，一定程度上是促進學生主動表現的設計。程序性卡點及課堂解決方案見表2。

三、策略性卡點

策略性卡點就是由于學生策略性知識缺乏所造成的對某個知識點的理解障礙。策略性知識是有關學習、思維和解決問題的一般策略的知識。策略性知識決定學習者學習能力的高低，學習能力高的學習者更加善于利用認知策略來幫助理解知識。特別是在面臨著復雜問題的時候，采取有效的策略，可以迅速地抓住問題的本質，抓住問題解決的關鍵點，把復雜的問題轉變為易于理解的簡單問題，從而實現深度理解。

例如雞兔同籠問題：籠子里有若干只雞和兔，從上面數，有8個頭，從下面數，有26只腳。雞和兔各有幾只？

教師如果過于簡單化處理，僵化地講解，例如強調“設雞求兔”或“設兔求雞”，學生雖然不理解，但照搬解法，也能求解出來，但如果換一個問題情境，學生就有可能不知所措。對這道題的教學，追求理解才是有效的教學，策略性知識缺乏是學生解決這道復雜問題的障礙，不懂得抓住問題的關鍵點，把復雜的問題轉換為簡單問題，不能透過問題看本質，導致策略性卡點。解決這個卡點，教師要給學生提供一個理解問題的支架，也就是策略性知識。對這道題進行分析，教材給出的解法是：

（1）如果籠子里都是雞，那么就有8×2=16只腳，這樣就多出26-16=10只腳;

（2）一只兔比一只雞多2只腳，也就是有10÷2=5只兔;

（3）所以籠子里有3只雞，5只兔。

對這種解法的理解，學生最不懂的地方是：為什么用10除以2，能得到兔的數量？這是這個問題的卡點，要理解這一點，教師需要給學生提供策略性知識。教師可轉換成以下問題：小明家里養了幾只兔子，每只兔子有4條腿，他要算家里兔子的腿總共有多少條，但不小心每只兔算少了兩條腿，一共算少了10條腿，問小明家里養了多少只兔？這道題對小學四年級學生來說很簡單，先做這題，再來講雞兔同籠“設雞求兔”“設兔求雞”的解法，學生就較為容易理解，這就是將復雜問題轉換成簡單問題的學習策略。

對于復雜問題的理解，教師通過提供策略性知識，幫助學生解決卡點是必要的。但由于復雜問題情境的多樣性，需要進一步進行變式練習，鞏固策略性知識的掌握，同時加深對此問題情境的理解，最終掌握這類問題的解決方法。對于復雜問題的變式練習，要掌握好情境改變的程度，設計兩個變式的情境，一個跟原問題差別很小的問題情境，例如這道題改變動物的類別、數量、文句的表達方式，但基本的情境（兩種動物一種四條腿一種兩條腿、已知頭和腳的數量）沒有變，這種情境筆者稱為“類情境”，原始題目的情境相應稱為“原情境”;另外一種是解決問題的方法沒有變，但情境有比較大的變化（例如不再是動物），這種情境筆者稱為“它情境”。復雜問題的變式練習，要從原情境的練習，過渡到類情境的練習，再過渡到它情境的練習，這樣的設計，才符合學生學習的最近發展區原理，才能使學生由淺到深、層層深入地理解知識的本質，最終達到對一類問題的完全洞悉。

注：本文系廣東省教育科研“十三五”規劃2018年度課題“基于深度學習的小學數學微課程設計研究”（課題批準號：2018YQJK013）研究成果。

責任編輯 羅 峰