祁連山南麓區(qū)域的大氣負(fù)荷動力學(xué)效應(yīng)研究
安旭偉,楊國林,孫學(xué)先,劉 濤,張 波
祁連山南麓區(qū)域的大氣負(fù)荷動力學(xué)效應(yīng)研究
安旭偉1,2,楊國林1,孫學(xué)先3,劉 濤1,張 波1,2
(1. 蘭州交通大學(xué) 測繪與地理信息學(xué)院,蘭州 730070;2. 地理國情監(jiān)測技術(shù)應(yīng)用國家地方聯(lián)合工程研究中心,蘭州 730070;3. 甘肅省地理國情監(jiān)測工程實(shí)驗(yàn)室,蘭州 730070)
地殼形變的大氣負(fù)荷效應(yīng)在沿海區(qū)域已得到了廣泛研究和應(yīng)用,但是在內(nèi)陸地區(qū),動力學(xué)效應(yīng)研究甚少。基于地面氣象觀測數(shù)據(jù)和全球氣壓模型數(shù)據(jù),給出了一種適合于內(nèi)陸地區(qū)的大氣負(fù)荷動力學(xué)效應(yīng)的計(jì)算方法。以中國祁連山南麓地區(qū)為例,研究了地殼形變和地面重力變化。研究結(jié)果表明:對于祁連山南麓地區(qū),大氣負(fù)荷對測站位移徑向分量的影響約為8.4 mm,而水平位移不足1.0 mm;對測站重力的影響約為6.4×10-8m/s2。大氣負(fù)荷的動力學(xué)效應(yīng)具有明顯的周期性和季節(jié)性,這種變化規(guī)律與周邊地區(qū)表現(xiàn)出較高的一致性。
球諧分析;移去恢復(fù);負(fù)荷格林函數(shù);大氣導(dǎo)納
0 引言
受各種地球動力學(xué)因素的影響,地球重力場和地面站點(diǎn)位置會隨時間發(fā)生變化。其中大氣負(fù)荷潮指的是,大氣在日月引潮力和太陽熱輻射的共同作用下,表現(xiàn)出的大氣壓周期性變化[1],在高精度的大地測量計(jì)算過程中,大氣負(fù)荷改正是不能被忽略的[2-4]。文獻(xiàn)[5]提出了大氣負(fù)荷效應(yīng)的負(fù)荷格林函數(shù)積分法與球諧函數(shù)法;文獻(xiàn)[2]基于朗曼(Longman)地球負(fù)荷理論,提出了靜態(tài)格林函數(shù)法;文獻(xiàn)[4]對中國6個全球定位系統(tǒng)(global positioning system, GPS)基準(zhǔn)站的大氣負(fù)荷效應(yīng)進(jìn)行了研究,指出測站徑向位移的大氣負(fù)荷效應(yīng)可達(dá)2~3 cm;文獻(xiàn)[6-8]利用球諧函數(shù)方法,給出了地表流體質(zhì)量負(fù)荷變化的動力學(xué)效應(yīng)公式;文獻(xiàn)[9]利用全球大氣壓實(shí)測數(shù)據(jù),計(jì)算了大氣負(fù)荷對地面重力變化的影響;文獻(xiàn)[10]結(jié)合地表水、大氣及海平面變化資料,提出了負(fù)荷形變場精化模型的已知負(fù)荷移去恢復(fù)法,建立了地面穩(wěn)定性變化定量辨識準(zhǔn)則。目前,將文獻(xiàn)[10]理論應(yīng)用于高原地區(qū)的研究成果相對較少,因此,有必要將這種方法落實(shí)到具體的某一個高原地區(qū),定量分析大氣負(fù)荷對內(nèi)陸地表的影響。
本文在全球大氣數(shù)據(jù)的基礎(chǔ)上,結(jié)合祁連山南麓區(qū)域內(nèi)氣象站的實(shí)測氣壓數(shù)據(jù),計(jì)算了大氣負(fù)荷對區(qū)域內(nèi)地殼形變以及地面重力變化的影響,目的是分析具體影響量級,從而獲得大氣負(fù)荷效應(yīng)的變化規(guī)律以及影響量。
1 負(fù)荷形變理論與移去恢復(fù)法
1.1 負(fù)荷形變理論
大氣負(fù)荷引起的地殼形變與重力變化都可以用相應(yīng)的等效水高變化來表示[11],即


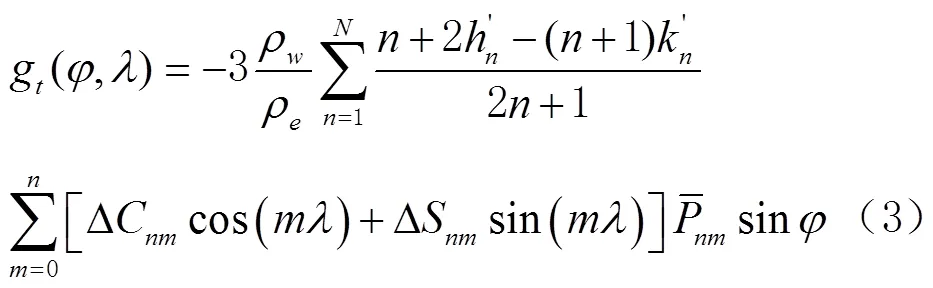


1.2 移去恢復(fù)法
移去恢復(fù)法主要流程見圖1。
2 研究區(qū)域和數(shù)據(jù)
2.1 研究區(qū)域
本文研究區(qū)域?yàn)椋?3.5°E~99.0°E,34.5°N~38.0°N),如圖2所示。
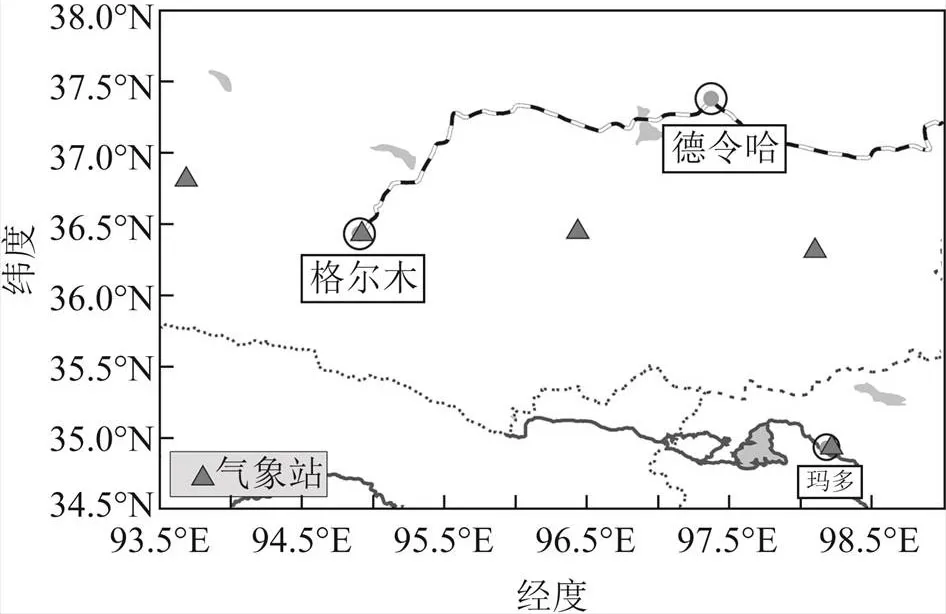
圖2 研究區(qū)域及氣象站點(diǎn)示意
2.2 數(shù)據(jù)來源
本文研究的全球大氣數(shù)據(jù)源自歐洲中期天氣預(yù)報(bào)中心(European Centre for Medium-Range Weather Forecasts,ECMWF)[13],該類數(shù)據(jù)的特點(diǎn)是覆蓋范圍廣、要素種類多、分辨率較高、記錄數(shù)據(jù)時次多等。使用的區(qū)域大氣壓數(shù)據(jù)來自于寒旱區(qū)科學(xué)數(shù)據(jù)中心的中國大氣同化驅(qū)動數(shù)據(jù)集(The China Meteorological Assimilation Driving Datasets for the SWAT Model, CMADS)[14],使用的是日均值氣壓數(shù)據(jù),精度為0.1 hPa。數(shù)據(jù)處理過程中,需要將空間分辨率改變?yōu)?.05°×0.05°,并使用派森(Python)程序?qū)⑵滢D(zhuǎn)換為月值數(shù)據(jù)。
3 地殼形變和重力變化計(jì)算分析
3.1 大氣負(fù)荷對地殼形變的影響
為了方便計(jì)算,本文使用的全球氣壓等效水高基準(zhǔn)是2011年10—12月,共3個月的月均值,所有的變化都是基于這一基準(zhǔn)而言,計(jì)算了2012年1月—2017年12月,共6年的大氣負(fù)荷對地殼形變的影響。
本文選取2015年3月、6月、9月與12月大氣負(fù)荷對地殼形變場影響的空間分布進(jìn)行分析,其中水平形變包括北方向以及東方向兩個部分,先分別計(jì)算,然后再進(jìn)行矢量合并,最后得到水平形變量的大小(矢量模的大小)。根據(jù)計(jì)算大氣負(fù)荷對祁連山南麓區(qū)域內(nèi)地殼形變的影響,其變化規(guī)律具有明顯的年周期性。區(qū)域影響變遷圖如圖3、圖4所示。
由圖3,圖4可知,大氣負(fù)荷對地殼垂直形變影響的最大變化量出現(xiàn)在德令哈周邊區(qū)域,大約為7.5 mm,這與該地區(qū)當(dāng)年氣壓變化量較大相符。而對水平形變的影響量較小,即使格爾木附近出現(xiàn)了最大水平形,但其變化變量也不足1.0 mm。就周期變化規(guī)律而言,大氣負(fù)荷對地殼形變影響在春夏季呈增大趨勢,在6月份左右達(dá)到最大,在秋冬季呈減小趨勢,在12月份左右降至最小。由于地表環(huán)境的復(fù)雜性,可能導(dǎo)致2012年、2013年、2015年的垂直形變最小值出現(xiàn)時間提前到10月份。就6年地殼形變的總體規(guī)律而言,與該區(qū)域夏季氣溫高、晝夜溫差較大,所引起的地表特征變化活躍相符合。
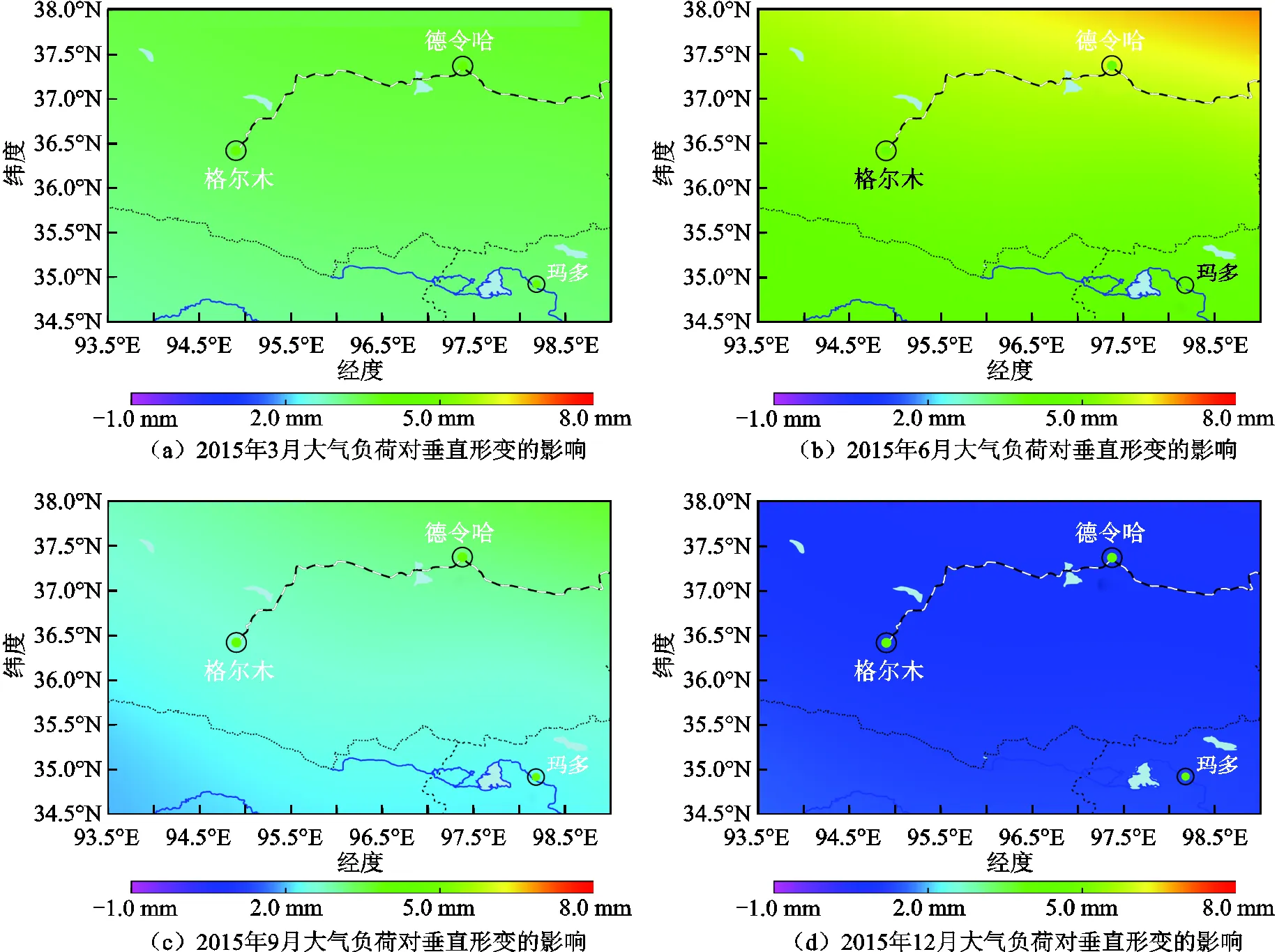
圖3 2015年大氣負(fù)荷對地殼垂直形變的影響
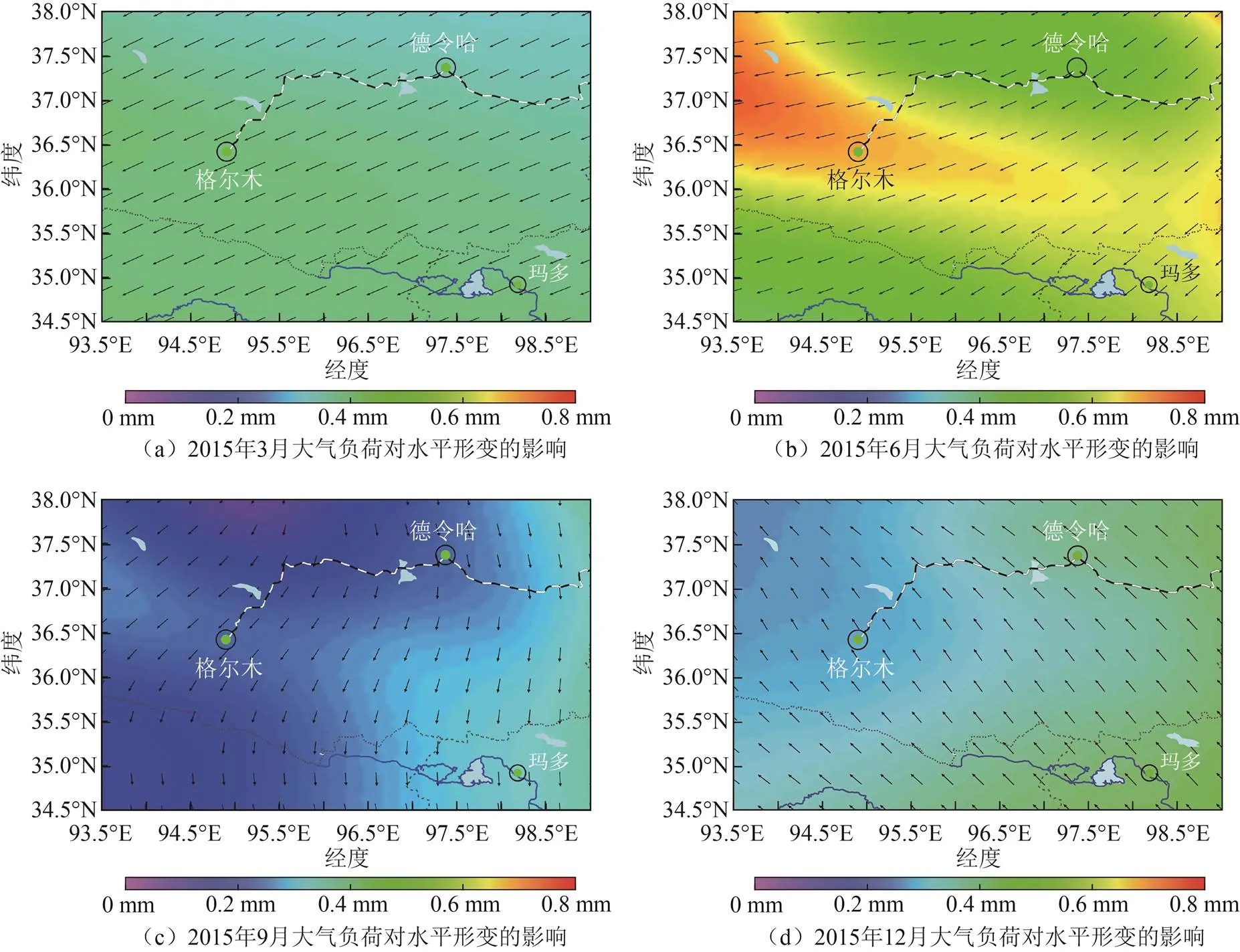
圖4 2015年大氣負(fù)荷對地殼水平形變的影響
3.2 大氣負(fù)荷對地面重力的影響
大氣負(fù)荷對地面重力變化總影響還包含直接影響,可以由大氣導(dǎo)納的方式求得[15],然后將兩種影響結(jié)果相加即得重力變化的總影響,本文選取了2015年3月、6月、9月與12月大氣負(fù)荷對地面重力影響的空間分布進(jìn)行分析,如圖5所示。
由圖5可知,大氣負(fù)荷對祁連山南麓區(qū)域的地面重力呈現(xiàn)周期性規(guī)律,春夏季主要表現(xiàn)為增大趨勢,在6月份左右達(dá)到最大值5.4×10-8m·s-2,較為顯著的空間分布出現(xiàn)在德令哈地區(qū)。秋冬季主要體現(xiàn)為減小趨勢。就整個研究區(qū)域祁連山南麓而言,年變化幅度可達(dá)6.4×10-8m·s-2。就6年地面重力變化總體來看,每年最大值出現(xiàn)的情況比較規(guī)律,一般在6月份左右;相比之下,最小值會提前到9月份、10月份出現(xiàn),這可能與該地區(qū)復(fù)雜的地表環(huán)境有關(guān)。
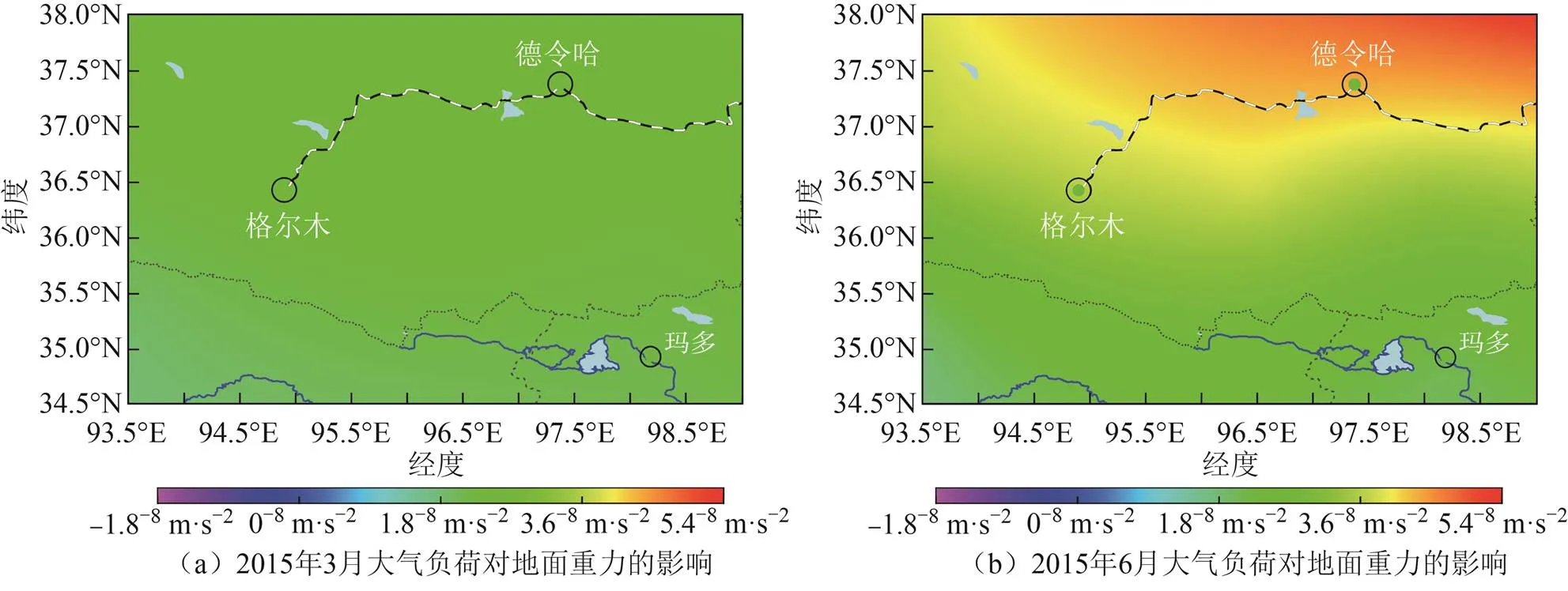
圖3至圖5所反映的周期性和季節(jié)性與研究區(qū)域周邊地區(qū)(如新疆地區(qū))的變化規(guī)律[16]具有較高的一致性。
3.3 統(tǒng)計(jì)分析
表1統(tǒng)計(jì)了2012—2017年大氣負(fù)荷對地殼形變及重力變化的標(biāo)準(zhǔn)差及年變化幅度信息,由于使用標(biāo)準(zhǔn)差統(tǒng)計(jì)方式不能完全揭示長周期占優(yōu)勢信號的變化特征,因此,本文在統(tǒng)計(jì)標(biāo)準(zhǔn)差的同時,也對其負(fù)荷影響的年變化幅度進(jìn)行了統(tǒng)計(jì)。表1中的年變化幅度即為6年中對應(yīng)負(fù)荷影響的最大值。

表1 大氣負(fù)荷對各種形變的影響統(tǒng)計(jì)
注:水平形變只統(tǒng)計(jì)其模的大小
表1結(jié)果顯示:大氣負(fù)荷對三種類型的年變化幅度依次為8.4 mm、不足1.0 mm和6.4×10-8m·s-2。其中,大氣負(fù)荷對垂直形變與地面重力的影響在2012—2017年間有減小的趨勢,如2012年最大值為8.1 mm與6.4×10-8m·s-2,2017年減小到6.1 mm與4.8×10-8m·s-2。均值由3.9 mm和2.7×10-8m·s-2減小到2.5 mm和1.5×10-8m·s-2。這說明除了大氣負(fù)荷這一影響因素外,還有其他因素(如土壤水、地下水等)也同樣會造成地殼形變與地面重力的變化,從而導(dǎo)致其形變量與變化量出現(xiàn)逐年減小的趨勢,具體原因有待進(jìn)一步分析。
本文選取了區(qū)域內(nèi)QHGE(青海格爾木)與QHMD(青海瑪多)兩個具有代表性的連續(xù)運(yùn)行參考站(continuously operating reference stations,CORS)的數(shù)據(jù),并將其形變量及變化量內(nèi)插至CORS站點(diǎn),結(jié)果如圖6、圖7所示。

圖6 QHGE站點(diǎn)大氣壓變化、垂直形變和重力變化
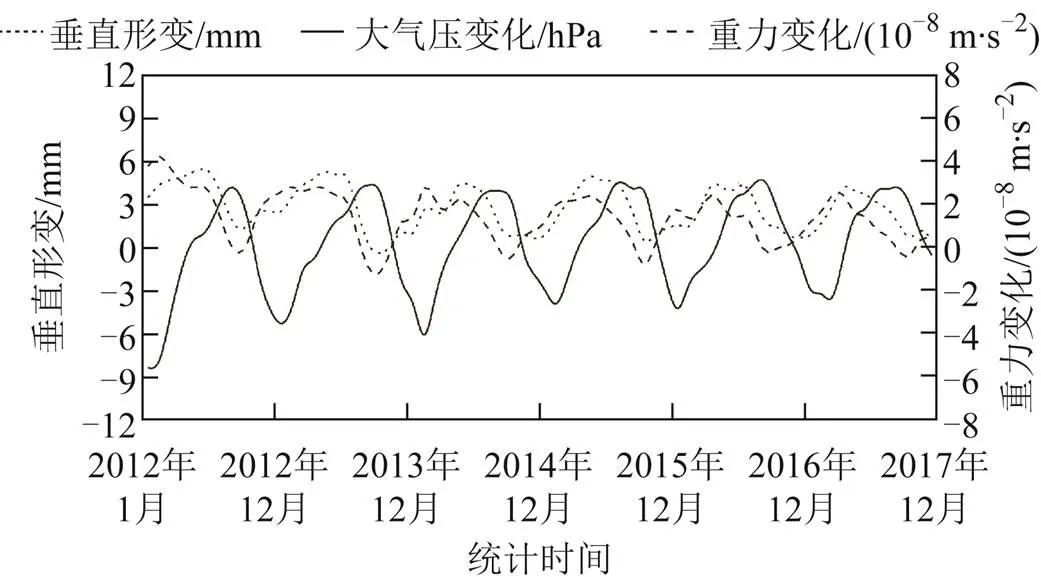
圖7 QHMD站點(diǎn)大氣壓變化、垂直形變和重力變化
由圖6,圖7可知,點(diǎn)形虛線和線型虛線代表的垂直形變及重力變化有明顯的周期性。例如,兩種線型所代表的的形變類型除2012年以外,都是以每年先增大后減小,隨時間而變化。另外還具有季節(jié)性變化規(guī)律,大氣負(fù)荷影響在每年春夏季最大,秋冬季最小。以QHGE站點(diǎn)為例,負(fù)荷形變春夏季增大的速度較慢,在6月份左右到達(dá)最大值,秋冬季減小的速度較快,在9月份左右到達(dá)最小值。反觀QHMD站點(diǎn)的重力變化曲線,2015年、2016年和2017年的峰值提前到3月份左右,這可能與該站點(diǎn)一定范圍內(nèi)的土壤水及地下水含量變化有關(guān)。縱觀整體形變規(guī)律,與中國大陸地區(qū)的氣候特征有明顯的聯(lián)系。同時可以發(fā)現(xiàn)隨著時間的推移,形變負(fù)荷的年變化幅度有所減小。
4 結(jié)束語
本文采用移去恢復(fù)法,在全球大氣壓數(shù)據(jù)的基礎(chǔ)上,結(jié)合祁連山南麓區(qū)域氣象站實(shí)測大氣壓數(shù)據(jù),計(jì)算了區(qū)域內(nèi)地殼形變及重力變化的負(fù)荷效應(yīng)影響特征。結(jié)果表明,大氣負(fù)荷具有年周期性以及季節(jié)性的變化特征。垂直形變的年幅度影響為8.4 mm左右;水平形變的影響不足1.0 mm。重力變化的年幅度影響最大為6.4×10-8m·s-2,且與大氣壓變化成負(fù)相關(guān)。大氣負(fù)荷的季節(jié)性表現(xiàn)為:春夏季達(dá)到最大值,其增大趨勢較為緩慢;秋冬季達(dá)到最小值,其減小趨勢較快。此結(jié)論與周邊區(qū)域的地殼動力學(xué)在變化范圍及影響特征具有較高的一致性。綜合6年的負(fù)荷形變可以發(fā)現(xiàn),年變化幅度影響有所減小。本文的方法如果應(yīng)用到富含水體的區(qū)域時,則需要在球諧系數(shù)基礎(chǔ)上考慮潮汐調(diào)和常數(shù)的計(jì)算。
[1] 王偉, 黨亞民, 章傳銀, 等. 基于 CORS 站網(wǎng)監(jiān)測三峽地區(qū)陸地水負(fù)荷對地殼形變和重力變化的影響[J]. 地球物理學(xué)報(bào), 2017, 60(3): 962-971.
[2] FARRELL W E. Deformation of the Earth by surface loads[J]. Rev Reviews of Geophysics & Space Physics, 1972, 10(3): 761-797.
[3] JEAN-PAUL B, PASCAL G, JACQUES H. Reduction of surface gravity data from global atmospheric pressure loading[J]. Geophysical Journal International, 2002, 149(2): 534-545.
[4] 張?jiān)娪? 鐘敏, 唐詩華. 我國GPS基準(zhǔn)站地殼垂直形變的大氣負(fù)荷效應(yīng)[J]. 武漢大學(xué)學(xué)報(bào)(信息科學(xué)版), 2006, 31(12): 1090-1093.
[5] LONGMAN I M. A Green’s function for determining the deformation of the Earth under surface mass loads: computations and numerical results[J]. Journal of Geophysical Research, 1963, 68(2): 485-496.
[6] SPRATT R S. Modeling the effect of atmospheric pressure variations on gravity[J]. Geophysical Journal International, 2010, 71(1): 173-186.
[7] MANGIAROTTI S, CAZENAVE A, SOUDARIN L, et al. Annual vertical crustal motions predicted from surface mass redistribution and observed by space geodesy[J]. Journal of Geophysical Research: Solid Earth, 2001, 106(B3): 4277-4292.
[8] MITROVICA J X, DAVIS J L, SHAPIRO I I. A spectral formalism for computing three-dimensional deformations due to surface loads: present-day glacial isostatic adjustment[J]. Journal of Geophysical Research: Solid Earth, 1994, 99(B4): 7075-7101.
[9] VANDAM T M, BLEWITT G, HELFIN M B. Atmospheric pressure loading effects on global positioning system coordinate determinations[J]. Journal of Geophysical Research, 1994, 99(B12): 23939-23950.
[10] 章傳銀, 李愛勤, 黨亞民, 等. CORS 網(wǎng)區(qū)域重力場變化與地面穩(wěn)定性跟蹤監(jiān)測方法[J]. 測繪科學(xué), 2019, 44(6): 29-36.
[11] WU Xiaoping, HELFIN M B, IVINS E R, et al. Seasonal and interannual global surface mass variations from multisatellite geodetic data[J]. Journal of Geophysical Research, 2006, 111(B9): B09401.
[12] 劉宇, 李愛勤, 俞志強(qiáng), 等. 大氣負(fù)荷效應(yīng)對浙江地區(qū)的影響分析[J]. 大地測量與地球動力學(xué), 2020, 40(6): 591-595.
[13] 楊成生, 張勤, 李振洪. ECMWF 資料的邊界層伸縮水汽加密算法[J]. 武漢大學(xué)學(xué)報(bào)(信息科學(xué)版), 2015, 40(1): 83-89.
[14] 孟現(xiàn)勇, 王浩, 雷曉輝, 等. 基于 CMDAS 驅(qū)動 SWAT 模式的精博河流域水文相關(guān)分量模擬、驗(yàn)證及分析[J]. 生態(tài)學(xué)報(bào), 2017, 37(21): 7114-7127.
[15] RAY R D, PONTE R M. Barometric tides from ECMWF operational analyses[J]. Annales Geophysicae, 2003, 21(8): 1897-1910.
[16] 王海濤, 王斌, 王偉, 等. 大氣負(fù)荷對新疆地區(qū)地殼形變和地面重力變化的影響[J]. 大地測量與地球動力學(xué), 2019, 39(2): 189-194.
Study on the dynamical effects of atmospheric load on the southern foot of Qilian Mountains
AN Xuwei1,2, YANG Guolin1, SUN Xuexian3, LIU Tao1, ZHANG Bo1,2
(1. Faculty of Geomatics, Lanzhou Jiaotong University, Lanzhou 730070, China;2. National-Local Joint Engineering Research Center of Technologies and Applications for National Geographic State Monitoring, Lanzhou 730070, China;3. Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, Lanzhou 730070, China)
At present, domestic researches on changes in surface characteristics of atmospheric loading effects was mainly concentrated in the southeastern coastal areas, while the study's researches in northwest plateau were poor. So this paper presented an improvement method: the global atmospheric model and regional atmospheric pressure data were used to improve the accuracy of local atmospheric load, calculated the impact of atmospheric pressure loading on crustal deformation and gravity changes in the southern piedmont of Qilian Mountains. Statistical analysis results showed that: the impact of atmospheric loading is mainly reflected in vertical deformation and ground gravity changes, and the impact of maximum annual magnitude is 8.4 mm and 6.4×10-8m/s2, while horizontal deformation is less than 1.0 mm. The atmospheric loading has obvious annual periodicity and seasonality, at the same time, this change law is consistent with the surrounding areas. However this method needs to consider calculation of the tidal harmonic constant if the method is applied to waterrich areas.
Spherical harmonic analysis; removal and restoration; Green's function; atmospheric admittance
P228
A
2095-4999(2021)02-0090-06
安旭偉,楊國林,孫學(xué)先,等. 祁連山南麓區(qū)域的大氣負(fù)荷動力學(xué)效應(yīng)研究[J]. 導(dǎo)航定位學(xué)報(bào), 2021, 9(2): 90-95.(AN Xuwei, YANG Guolin, SUN Xuexian, et al. Study on the dynamical effects of atmospheric load on the southern foot of Qilian Mountains[J]. Journal of Navigation and Positioning, 2021, 9(2): 90-95.)
10.16547/j.cnki.10-1096.20210214.
2020-07-27
國家重點(diǎn)研發(fā)計(jì)劃課題項(xiàng)目(2016YFC0803106);國家自然科學(xué)基金項(xiàng)目(41764001,41761088);蘭州交通大學(xué)優(yōu)秀平臺支持項(xiàng)目(201806);蘭州交通大學(xué)天佑創(chuàng)新團(tuán)隊(duì)項(xiàng)目(TY202001)。
安旭偉(1995—),男,甘肅平?jīng)鋈耍T士研究生,研究方向?yàn)榇蟮販y量數(shù)據(jù)處理。
楊國林(1978—),男,甘肅定西人,博士,副教授,研究方向?yàn)榇蟮販y量理論及數(shù)據(jù)處理。

