單縫衍射測量不同直徑細絲的誤差分析研究
王麗光,朱長明,孔文婕
(廣西師范大學物理科學與技術學院,廣西 桂林 541004)
1 引言
1.1 單縫衍射
光具有沿直線傳播、折射、反射、波動等多種特性,而衍射是光波動性的重要體現,也是光波在傳播過程中的重要屬性之一。現階段,光的衍射在我們學習生活和科學發展中得以廣泛應用,例如:根據DNA 分子衍射圖樣得出DNA 結構是雙螺旋結構。在1962 年沃森、克里克和威爾金斯三人因此研究成果獲得了共同獲得了諾貝爾生理學或醫學獎。我們無可否認衍射現象對生物學界的重要貢獻,在科學研究中有著舉足輕重的地位。大學物理實驗中,當遇到不可直接測量的微小變化量時,可以利用單縫衍射法測量微小量,例如測量單縫寬度、細絲直徑亦或是激光波長。
單縫衍射是指光在傳播過程中遇到障礙物時會繞過障礙物繼續傳播到障礙物的幾何陰影區域,并在觀察屏呈現出光強分布不均勻的衍射圖樣[1]。單縫衍射通常分為兩類:夫瑯禾費衍射、菲涅爾衍射。本文對夫瑯禾費衍射測量不同金屬細絲直徑進行簡要介紹,并對實驗結果及誤差進行分析。
1.2 實驗誤差
實驗過程中導致誤差出現的因素有很多,性質上分為系統誤差、隨機誤差及過失誤差。容易理解的是過失誤差是指由于操作不當、外界因數干擾等原因而造成實驗數據結果明顯失真,這是可以避免的一類誤差。
系統誤差是指在相同實驗條件下測量相同物理量時,保持恒定或以可預知方式變化的測量誤差分量,又稱規律誤差。通常來源于儀器誤差、理論誤差、個人誤差。系統誤差不可避免,但產生系統誤差的主要原因可以從實驗條件等方面得出,并設計出新的改進方案來降低系統誤差[2]。
隨機誤差,俗稱偶然誤差,它是指測量結果與同一待測量的多次測量的平均結果之差。隨機誤差的產生因素錯綜復雜,任何外界或內部的影響都可能導致隨機誤差的產生。大多測量結果其數值都會服從正態分布規律,從中可獲取絕對誤差δ和標準誤差ζ,并運用貝塞爾法對標準誤差ζ進行估算,得出近似標準偏差取而代之,而算數平均值也隨實驗次數增多而具有離散性,定義用表示其標準偏差。與系統誤差相同的是隨機誤差也只可降低不可避免。
1.3 不確定度
不確定度是測量過程中產生的各種誤差使得測量結果而不被肯定的程度。它含有多個分量,按統計性質劃分,可以分為A 類不確定度分量和B 類不確定度分量[3]。A 類不確定度來源于隨機誤差,它可以用統計規律來計算,即

它與算術平均值的標準偏差一致;而B 類不確定度與系統誤差有關聯,它不符合統計規律,通常用儀器的標準誤差來衡量,即uB=,最后最后得出合成不確定度為u=。
2 實驗原理及測量方法
2.1 單縫衍射實驗原理
夫瑯禾費單縫衍射要滿足從光源到狹縫的入射光為平行光,從狹縫傳播到接收屏的出射光也是平行光,可利用兩個透鏡來觀察衍射現象,一個透鏡置于光源與狹縫之間,另一個透鏡則置于狹縫與接收屏之間。如圖1 所示,在透鏡L1的焦平面上置一波長為λ的單色光源S,經透鏡L1射出垂直于寬度為d的狹縫的平行光,若d很小,根據惠更斯-菲涅耳原理,同一波面任一面元均可視為一新的次波源,再由這些次波在空間傳播并于某位置相遇而產生相互干涉疊加,從透鏡L2出射后,可以在處于透鏡L2焦平面的接收屏上看到一組平行于狹縫且明暗相間的衍射條紋,其特點為中央明條紋最亮最寬,在其兩側分布的則是較弱的明暗相間的條紋[4-5]。

圖1 單縫衍射
根據菲涅爾半波帶法得出在Ik點出現亮條紋的條件是
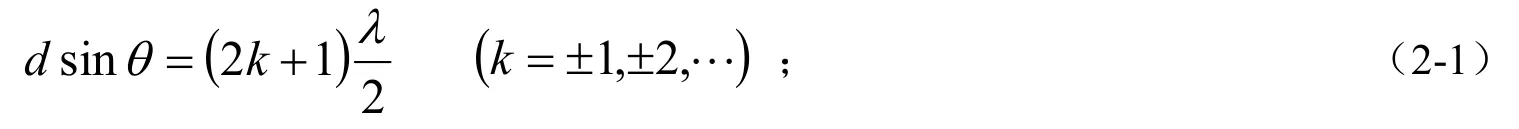
在Ik點出現暗條紋的條件是

假設透鏡L2距離觀察屏為?時,第k級亮條紋與衍射圖樣中心的距離為Rk,則,由于φ是極小角,存在 sinφ≈tanφ,根據式(2-1)可得:

根據巴比涅定理,同為互補障礙物的細絲與狹縫產生相同衍射圖樣,即可用縫寬的測量方法測量細絲直徑[6]。如圖2 所示,產生暗條紋的條件是

圖2 細絲產生的衍射

同理,θ角極小,sinφ≈tanφ,根據式(2-4)可得細絲直徑

式中L為細絲到測微目鏡的距離,為暗紋間距。
2.2 單縫衍射測量細絲直徑的實驗裝置及測量方法
為了得到更為準確的實驗結果,這里采用了激光光源,相比其他普通光源,它的高亮度可以使圖像更清晰,有利于觀察。在激光器后加一個擴束鏡來減小發散角,使激光光束變為平行光束。將狹縫1 調節至一定寬度就可獲得一條線光源,用于產生一級衍射;若在測微目鏡中觀察到的衍射圖樣暗淡模糊,無法較為準確地辨別出明暗條紋交界線,就可以調節狹縫1 的寬度獲得適當的光強;用狹縫2 遮住狹縫1 衍射光一側一級以上的衍射條紋,使最亮的零級光照在細絲上;遮光條用于擋住細絲產生的衍射條紋中的零級條紋,避免測量時受零級強光的影響;測量衍射暗紋間距S由測微目鏡讀取獲得;米尺用于讀出細絲到測微目鏡的距離L。實驗中激光束須平行光學平臺上的水平米尺,并在光學元件等高共軸后才能進行實驗,并利用式(2-5)計算細絲直徑d。
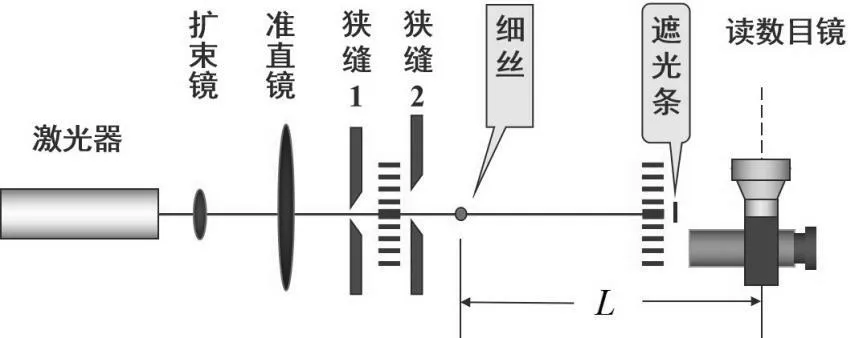
圖3 單縫衍射測量細絲直徑的實驗裝置

圖4 實驗裝置實物圖
3 實驗結果的誤差及不確定度分析
利用單縫衍射對6 根不同直徑細絲進行多次測量求平均,得出相關實驗數據如表1~表6。

表1 細絲1 的直徑測量 mm

表2 細絲2 的直徑測量 mm

表3 細絲3 的直徑測量 mm

表4 細絲4 的直徑測量 mm

表5 細絲5 的直徑測量 mm

表6 細絲6 的直徑測量 mm
3.1 系統誤差
在此實驗中,系統誤差導致實驗結果不精確是不可避免的。在理論因素上有實驗方法的不完善所導致的誤差;在儀器設備上有來源于儀器本身的缺陷或精度不高而導致的誤差,例如利用讀數顯微鏡獲取數據信息存在著不精確性;在環境因素上,由于這是一個光學實驗,對外界環境的遮光有著極高的要求,不絕對遮光也會影響實驗結果,從而產生誤差。
3.2 隨機誤差
本實驗中各種微小變動都會引起隨機誤差,比如,改變光學元器件間距時引起的變動,外界環境的變動,在肉眼讀取讀數顯微鏡中刻度尺上數據的變動等,這些因素最終導致測量值在平均值上下變動,而與之對應的差值即為測量的隨機誤差。根據算術平均值公式,可以進一步求出用單縫衍射測量細絲直徑的精度,如表7 所示。

表7 單縫衍射測量不同細絲直徑精度
3.3 不確定度
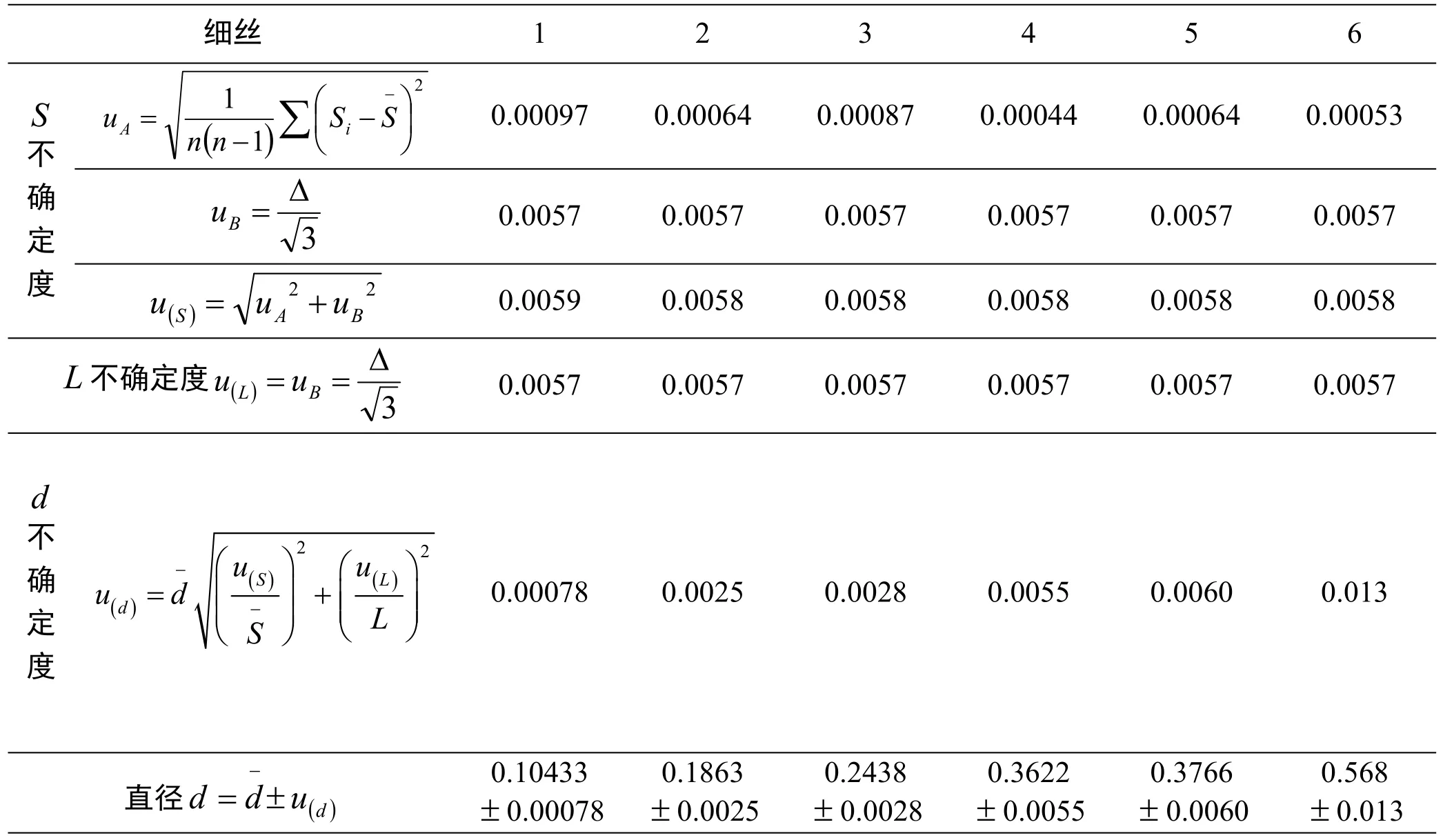
表8 測量不同細絲直徑的不確定度
4 結論
利用單縫衍射測量細絲直徑能獲得更高精度,相比于傳統的螺旋測微器法測量,前者可精確到0.0001mm,后者精確到0.001mm。通過誤差分析研究表明,在利用單縫衍射測量細絲直徑實驗中,實驗結果的不確定度與細絲直徑密切相關。細絲直徑更細的情況下,測量值的不確定度更小,測量結果更準確;反之在細絲直徑較粗的實驗中,測量值的不確定度更大,實驗結果更加偏離真值。

