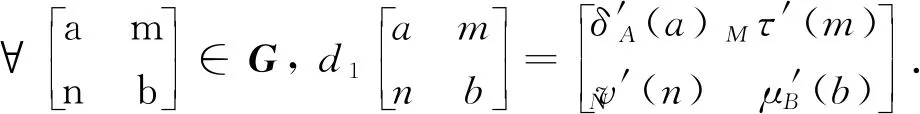交換半環(huán)上廣義矩陣代數(shù)的Jordan導(dǎo)子

莊金洪， 陳艷平， 譚宜家

(1. 福建商學(xué)院信息工程學(xué)院, 福建 福州 350012; 2. 福州大學(xué)數(shù)學(xué)與計算機科學(xué)學(xué)院, 福建 福州 350108)

0 引言

關(guān)于Jordan導(dǎo)子已有很多研究. 1957年， 文獻(xiàn)[1]證明了特征不等于2的素環(huán)上每個Jordan導(dǎo)子都是導(dǎo)子， 該結(jié)果被推廣到不同的環(huán)和代數(shù)上[2- 5]. 文獻(xiàn)[4]證明了三角代數(shù)上 每一個Jordan導(dǎo)子是導(dǎo)子. 近年來， 人們致力于將三角代數(shù)的線性映射理論發(fā)展到廣義矩陣代數(shù)的情形[6-8]. 廣義矩陣代數(shù)的線性映射研究主要是在交換環(huán)的基礎(chǔ)上進(jìn)行討論的， 但對于交換半環(huán)上廣義矩陣代數(shù)的線性映射研究比較少. 因此, 本研究將探討交換半環(huán)上廣義矩陣代數(shù)的Jordan導(dǎo)子、 導(dǎo)子與反導(dǎo)子.

1 預(yù)備知識

定義1[9]設(shè)R是一非空集合, “+”與”·”是定義在R中的兩個代數(shù)運算. 如果以下條件成立：

1) (R, +, 0)是一個交換幺半群， 其中0為R的加法恒等元；

2) (R, ·, 1)是一個幺半群， 其中1為R的乘法恒等元；

3) 對任意的a,b,c∈R, 均有a(b+c)=ab+ac, (a+b)c=ac+bc；

4) ?a∈R, 0a=a0=0；

5) 0≠1.

則稱R為一個半環(huán)， 記為(R, +, ·, 0, 1)或簡記為R. 這里， 加法恒等元0稱為半環(huán)R的零元， 乘法恒等元1稱為R的單位元.

如果?a,b∈R, 均有ab=ba, 則稱半環(huán)R是交換的. 如果?a,b∈R, 由a+c=b+c可推岀a=b,則稱c是加法可消的. 如果R的所有元素都是加法可消的， 那么稱半環(huán)R是加法可消的. 對于a∈R, 如果存在b∈R, 使得:a+b=0, 則稱a是R中的可反元， 并記b=-a， 這時， ?c∈R, 定義c-a=c+(-a).

定義2[9]設(shè)R為半環(huán)， (M, +, 0)為交換幺半群， 若存在從R×M到M的一個映射(r,m)|→rm， 滿足下列五個條件， 即對于任意r,r′∈R,m,m′∈M， 均有:

Ⅰ)r(m+m′)=rm+rm′; Ⅱ) (r+r′)m=rm+r′m;

Ⅲ) (rr′)m=r(r′m); Ⅳ) 1Rm=m; Ⅴ)r0=0=0m.

則稱M為半環(huán)R上的一個左半模， 簡稱左R-半模.

一個左R-半模M稱為忠實的, 如果?r,r′∈R, 當(dāng)對于所有m∈M, 均有rm=r′m時,r=r′. 類似地， 可定義半環(huán)R上的右半模和忠實右半模.

設(shè)R和S是半環(huán)， (M, +, 0)是一個交換幺半群. 稱(M, +, 0)是一個(R,S)-雙半模， 如果M既是左R-半模， 又是右S-半模， 且?r∈R,m∈M,s∈S, 均有: (rm)s=r(ms)成立.

定義3[9]設(shè)R是一個交換半環(huán), (A, +, ·, 0, 1)是一個半環(huán). 如果(A, +, 0)是R上的一個左半模, 且?r∈R,x,y∈A, 均有：r(xy)=(rx)y=x(ry)成立, 則稱A是R上的一個代數(shù).

定義4設(shè)A,B是半環(huán)R上的一個代數(shù)，M，N是(A,B)-雙半模，η:M→N是一個映射. 如果?x,y∈M,a∈A，b∈B,η(x+y)=η(x)+η(y),η(ax)=aη(x)，η(xb)=η(x)b, 則稱η為M到N的(A,B)-雙半模同態(tài).

定義5[10]設(shè)B是交換半環(huán)R上的代數(shù)，MB是右B-半模，BN是左B-半模，M×N是集合M,N的卡氏積， (V, +, 0)是一個交換幺半群. 映射f:M×N→V稱為B-平衡的， 如果?m,m′∈M,n,n′∈N,b∈B, 均有:

ⅰ)f(m+m′,n)=f(m,n)+f(m′,n)； ⅱ)f(m,n+n′)=f(m,n)+f(m,n′)；

ⅲ)f(mb,n)=f(m,bn)； ⅳ)f(m, 0)=0=f(0,n).

定義6[10]設(shè)B是交換半環(huán)R上的代數(shù)，MB是右B-半模，BN是左B-半模， (V, +, 0)是交換幺半群,f:M×N→V是B-平衡映射. 二元組(V,f)稱為MB和BN張量積， 如果對任意給定的交換幺半群(W, +, 0)和任意的B-平衡映射α:M×N→W， 存在唯一的半群同態(tài)β:V→W， 使得α=β°f， 記V=M?BN，f(m,n)=m?n.

命題1[10]設(shè)(M?BN, ?)是半模MB和BN的張量積, 那么?m,m′∈M,n,n′∈N,b∈B, 均有:

② (m+m′)?n=m?n+m′?n,m?(n+n′)=m?n+m?n′；

③ (mb)?n=m?(bn)；

④m?0=0=0?n.

設(shè)A,B是交換半環(huán)R上的代數(shù)，AMB,BNA均是雙半模， ?m∈M,n∈N,a,b∈A, 定義a(m?n)=(am)?n, (m?n)b=m?(nb), 則由文獻(xiàn)[10]知， 張量積M?BN是(A,A)-雙半模； 類似地， 張量積N?AM是(B,B)-雙半模.

定義8設(shè)A是R上的一個代數(shù)，d:A→A是一個R-線性映射. ?a,b∈A, 如果d(ab)=d(a)b+ad(b), 則稱d為A的一個導(dǎo)子； 如果d(ab)=d(b)a+bd(a), 則稱d是一個反導(dǎo)子； 如果d(ab+ba)=d(a)b+ad(b)+d(b)a+bd(a), 則稱d是一個Jordan導(dǎo)子. 如果存在可反元g∈A, 使得d(a)=ag-ga=ag+(-g)a， 則可驗證d是A的一個導(dǎo)子， 稱d為由g誘導(dǎo)的內(nèi)導(dǎo)子， 記為dg.

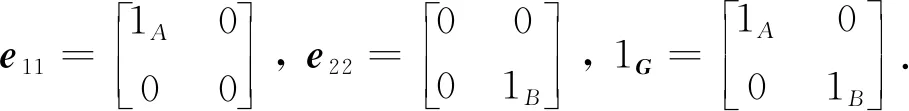
2 主要結(jié)果及其證明

引理1[11]設(shè)R是一個交換半環(huán),A是R上的一個代數(shù)，Δ:A→A是A上的一個Jordan導(dǎo)子. 那么?a∈A, 均有Δ(a2)=Δ(a)a+aΔ(a).

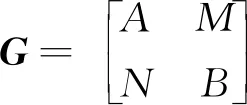
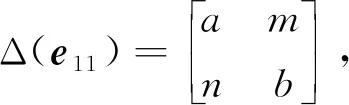
Δ-dg2=Δ2， 唯一性得證.

由引理2知， 想要獲得廣義矩陣代數(shù)G的Jordan導(dǎo)子的結(jié)構(gòu)， 只需給岀廣義矩陣代數(shù)G上滿足Δ(e11)=0的Jordan導(dǎo)子Δ的結(jié)構(gòu)即可.

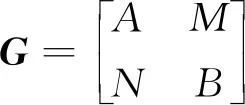
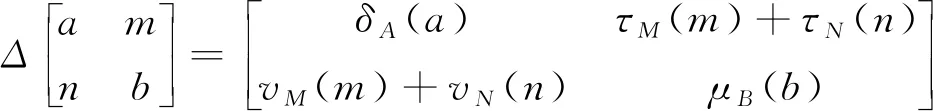
(1)

其中：δA:A→A，μB:B→B分別是A和B上的Jordan導(dǎo)子；τM:M→M，vN:N→N，τN:N→M，vM:M→N均為R-線性映射. 同時， ?a∈A,b∈B,m,m′∈M,n,n′∈N， 以下7點均成立：

1)δA(mn)=τM(m)n+mvN(n),μB(nm)=vN(n)m+nτM(m)；

2)τM(am)=δA(a)m+aτM(m),vM(am)=vM(m)a；

3)τM(mb)=τM(m)b+mμB(b),vM(mb)=bvM(m)；

4)vN(bn)=μB(b)n+bvN(n),τN(bn)=τN(n)b；

5)vN(na)=vN(n)a+nδA(a),τN(na)=aτN(n)；

6)mvM(m)=τN(n)n=0,vM(m)m=nτN(n)=0；

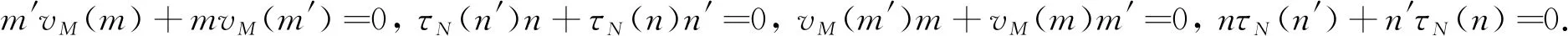
證明 充分性可以通過直接驗算證明， 下證必要性.

由于Δ:G→G是一個Jordan導(dǎo)子， 故?X,Y∈G, 有：

Δ(XY+YX)=Δ(X)Y+XΔ(Y)+Δ(Y)X+YΔ(X)

(2)

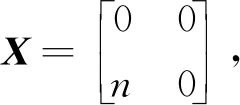
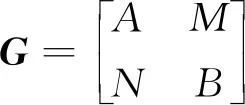
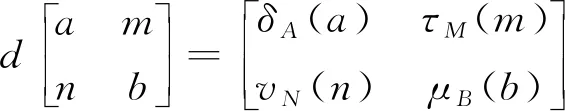
(3)

其中：δA:A→A和μB:B→B分別是A與B上的導(dǎo)子；τM:M→M和vN:N→N均為R-線性映射. 同時， ?a∈A,b∈B,m∈M,n∈N， 均有：

Ⅰ)δA(mn)=τM(m)n+mvN(n),μB(nm)=vN(n)m+nτM(m)；

Ⅱ)τM(am)=δA(a)m+aτM(m),τM(mb)=τM(m)b+mμB(b)；

Ⅲ)vN(bn)=μB(b)n+bvN(n),vN(na)=vN(n)a+nδA(a).

證明 通過直接驗算可證充分性， 下證必要性.

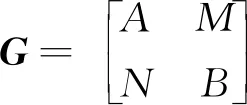
(4)

其中:τN:N→M，vM:M→N是R-線性映射. 同時?a∈A,b∈B,m,m′∈M,n,n′∈N, 均存在：

ⅰ)vM(am)=vM(m)a，vM(mb)=bvM(m),τN(na)=aτN(n),τN(bn)=τN(n)b;

ⅱ)mvM(m′)=τN(n)n′=0,vM(m)m′=nτN(n′)=0.

證明 通過直接計算可得h是G的反導(dǎo)子, 故充分性得證， 下證必要性.

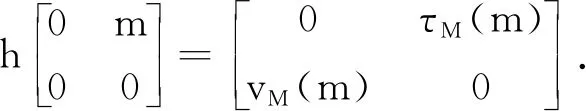
因為h是G的一個反導(dǎo)子， 所以?X,Y∈G, 下式成立：

h(XY)=h(Y)X+Yh(X)

(5)

類似可證， 當(dāng)N是忠實的(B,A)-雙半模時， 結(jié)論也成立. 證畢.

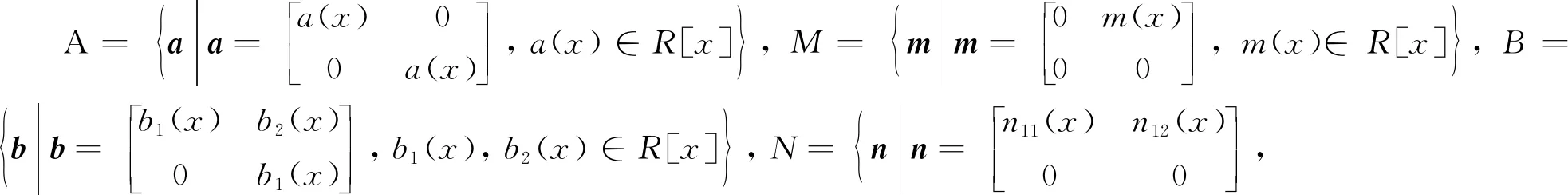
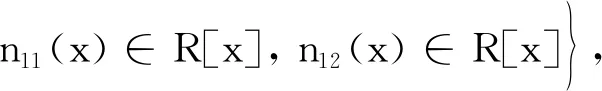
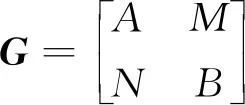
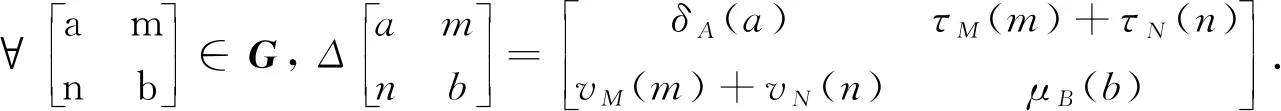
由于τM:M→M，vN:N→N，τN:N→M，vM:M→N均為R-線性映射且滿足定理1中的1)～7). 所以這些映射滿足定理2中的Ⅰ)～Ⅲ)和定理3中的ⅰ).

又由已知條件可得： ?m,m′∈M,n,n′∈N，mvM(m′)=τN(n)n′=0,vM(m)m′=nτN(n′)=0. 再由定理3知，h是G的反導(dǎo)子.

類似可證， 當(dāng)N是忠實的(B,A)-雙半模時， 結(jié)論也成立. 下證唯一性.