EPS土工泡沫緩沖層的抗震效果數值模擬

吳繼紅, 吳文豪， 謝志濤

(1. 江西省鷹潭市城市建設投資發展有限公司， 江西 鷹潭 335000； 2. 華東交通大學， 江西省巖土工程基礎設施安全與控制重點實驗室， 江西 南昌 330013； 3. 福州大學土木工程學院， 福建 福州 350108)

0 引言

擋土墻是許多基礎設施項目的組成部分， 很多情況下， 擋土墻是防止土壤失穩的首選措施. 在地震易發區， 除了靜土壓力外， 擋土墻還需要抵抗地震引起的振動增量. 焦方輝等[1-2]結合汶川震區調查資料， 利用大型振動臺模型試驗， 分析碎石土填料的巖石場地重力式擋土墻的地震土壓力及其分布規律. 馬少俊等[3]采用擬動力法推導并給出地震作用下擋土墻抗滑穩定安全系數的計算表達式. 文暢平[4]基于3個基覆邊坡模型的大型振動臺模型試驗， 研究重力式擋墻、 樁板式擋墻、 格構式框架結構等支擋結構的地震動位移模式及其變化規律. 任傳健[5]采用振動臺模擬試驗和數值方法， 對地震作用下重力式擋土墻的動力響應進行分析研究. 謝偉等[6]基于擬靜力法原理， 利用極限分析上限定理對地震作用下擋土墻地基極限承載力進行了求解. 上述對擋土墻抗震的研究主要在于揭示擋土墻自身的抗震特性， 均未涉及抗震措施的研究. 然而擋土墻尤其是重力式擋土墻的抗震措施， 即如何更經濟有效地減小地震作用引起的土體振動增量是擋土墻性能化設計中的一個重要因素.

聚苯乙烯泡沫(expanded polystyrene, EPS)是一種輕型高分子聚合物. 其具有自重輕、 耐久性好、 抗震性能好等特點， 是用于減弱動載對土體結構擾動的理想材料[7]. 近年來， 眾多學者對EPS材料用作抗震緩沖層的設計進行了研究. Nishant等[8]建立有限元模型研究EPS材料作為隧道隔震有效緩沖層的可行性. Zarnani等[9]利用FLAC研究EPS材料對擋土墻緩沖性能的影響. AbdelSalam[10]等在實驗數據基礎上建立淺埋隧道的數值模型， 研究了設置不同厚度的EPS夾層對作用在隧道上的豎向應力的緩沖效果. 潘詩婷等[11]通過擋土墻模型試驗， 在擋土墻面填充緩沖層， 分別測定擋土墻填充緩沖層前后的靜止土壓力和主動土壓力. 上述研究都表明EPS土工泡沫具有良好的減振性能， 但是EPS作為擋土墻的抗震緩沖層在土體振動增量控制方面的研究還不夠全面. 為此本文采用Plaxis軟件建立有限元模型， 通過數值參數分析研究土體與擋土墻間填充EPS土工泡沫時的減振緩沖效果， 以期為擋土墻抗震設計提供有益的指導.

1 模型概述

圖1 計算模型示意圖(單位： m)

本次模擬擋土墻采用4 m和8 m兩種高度的重力式擋土墻， 墻體材料為混凝土. 土體部分由下層地基土和上層回填土構成， 采用莫爾-庫侖破壞準則， 不考慮含水率影響， 不附加瑞利型阻尼. 擋土墻與回填土之間緩沖層材料為EPS土工泡沫， 模型材料參數具體見表1. 模型長度為50 m， 高度為10 m， 圖1是計算模型示意圖.

表1 模型材料參數

2 計算分析及評價指標

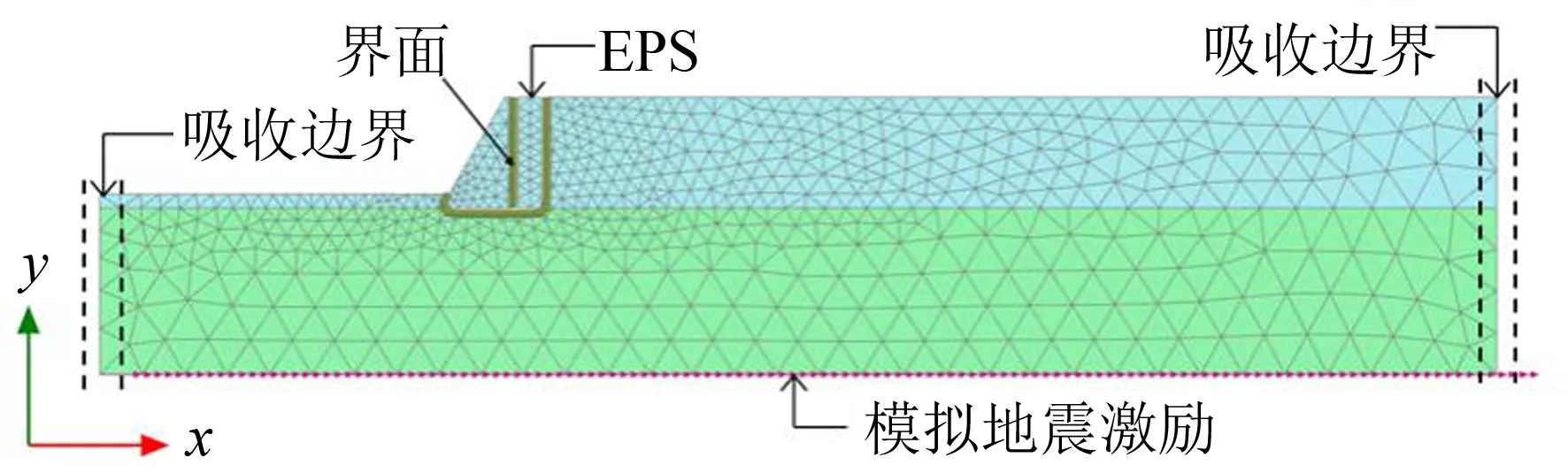
圖2 模型的有限元網格劃分

采用Plaxis有限元程序建立二維模型， 對高4和8 m的重力式擋土墻在地基受頻率3 Hz和不同振幅強度(0.1g～ 0.7g)的簡諧激勵下的動力反應進行分析. 在有限元網格的底部施加水平線位移， 以正弦加速度的形式施加水平簡諧激勵以此來模擬地震作用. 在墻體與土體、 EPS材料與土體、 EPS材料與墻體間設置界面元素， 粗糙系數為0.1.

數值模型的建立采用分段施工方法， 分階段施工包括3個階段， 第1階段： 水平地基土的布置； 第2階段： 混凝土擋土墻施工、 EPS材料布置， 回填土的放置； 第3階段為模擬地震動力分析. 圖2是模型的網格劃分， 模型土體部分左右邊界采用粘性邊界[12-13]來吸收水平激勵產生的波能， 避免在邊界反射.

EPS厚度相對于墻高做歸一化處理， 即EPS厚度與擋土墻高度的比值， 表示為tr. 對墻體底部水平位移變化量、 墻體轉動角度的變化量和側向推力增量進行評估， 以如下表達式為評價標準[14].

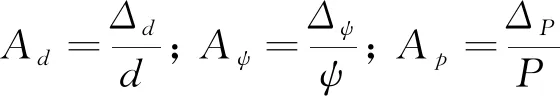
(1)

式中：Ad表示墻體水平位移變化率；Aψ表示墻體轉角變化率；Ap表示側向推力變化量；Δd為有EPS緩沖層和無EPS緩沖層時水平位移的差值；Δψ為有EPS緩沖層和無EPS緩沖層時墻體轉角的差值；ΔP為有EPS緩沖層和無EPS緩沖層時側向推力的差值；d，ψ，p分別為無EPS緩沖層時墻體的水平位移、 轉角和側向水平推力.

3 結果與分析

3.1 EPS緩沖層對墻體水平位移增量的影響

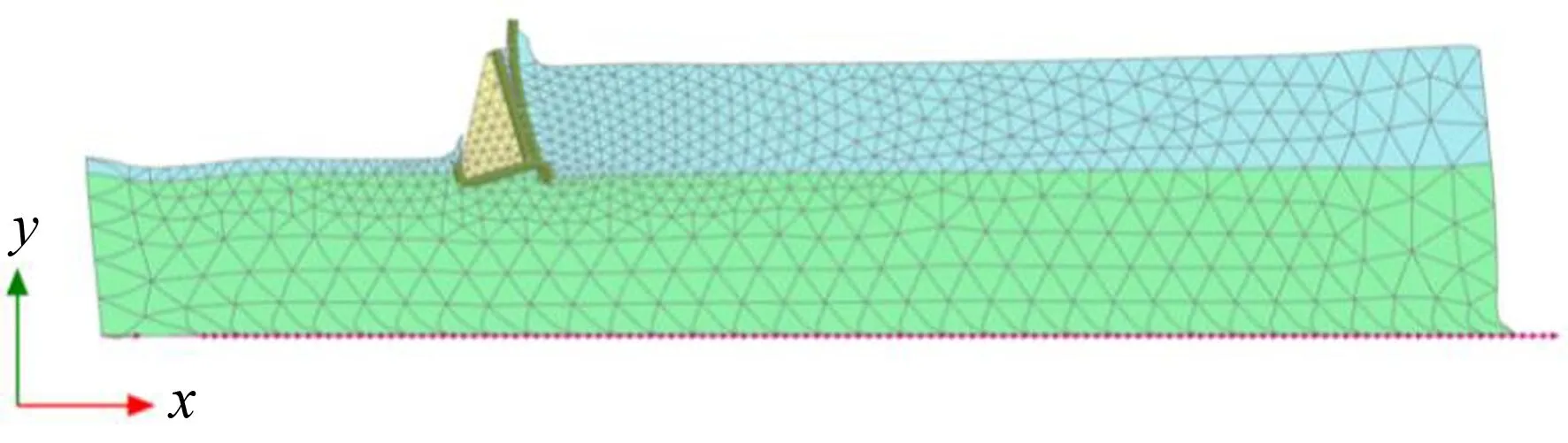
圖3 振幅為0.7g工況時的模型變形圖

振源頻率為3 Hz， 采用0.1g、 0.3g、 0.5g和0.7g不同振幅的正弦加速度信號， 分別計算設置EPS歸一化厚度tr為5%、 10%、 20%、 40%和60%的工況墻體底角處的水平位移與沒有設置EPS時的工況. 圖3是振幅取0.7g，tr取10%時計算完成后的網格變形， 可見， 在水平簡諧激勵作用下， 擋土墻發生明顯的位移和旋轉. 考慮的兩種壁高對水平位移的隔離效率， 利用公式(1)計算出減振效率， 圖4是4、 8 m高的墻體底部水平位移變化量Ad與EPS歸一化厚度tr之間的關系.

由圖4(a)可知， 振動強度從0.5g增加到0.7g時Ad增加不明顯.tr在5%～10%范圍內Ad有短暫降低， 不同振幅強度時Ad均呈現增加趨勢， 當tr超過20%后增加tr對Ad的影響不大，tr不再有明顯變化. 由圖4(b)可知，Ad最初隨tr線性增加， 達到一個值，tr為10%， 然后接近Ad為50%的極限值， 當tr超過20%后， 繼續增加歸一化厚度時， 墻體水平位移隔離效率基本維持不變. 由于EPS與土體間彈性模量的差異使得更多的振動能量在交界面被反射， 且少量透射波被EPS材料吸收.

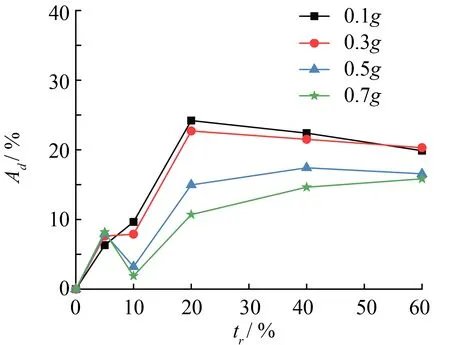
(a) 擋土墻高4 m

3.2 EPS緩沖層對墻體轉角增量的影響

保持振源頻率為3 Hz不變， 采用0.1g、 0.3g、 0.5g和0.7g不同振幅的正弦加速度信號， 分別計算設置EPS厚度tr為5%， 10%， 20%， 40%和60%的工況與沒有設置EPS時的工況墻體頂端右側邊緣角點的水平位移， 與節3.1中計算出的相對應工況墻底端的水平位移的差值， 通過位移的變化差值與豎向墻高的比值計算出轉角， 利用公式(1)計算得出隔離效率Aψ. 圖5是4、 8 m高的墻體頂部轉角變化量Aψ與EPS厚度tr之間的關系之間的關系.

由圖5(a)可知，tr較小時Aψ為負值， 此時EPS緩沖層并不能有效提高Aψ； 在tr超過10%后隔離效率緩慢提高；tr超過40%后繼續增加tr， 隔離效率基本沒有變化. 由圖5(b)可知，tr=20%為緩沖層的最佳厚度， 厚度超過20%時， 轉角的隔離效率呈下降趨勢. 因此， 對于4 m高的擋土墻， EPS厚度最佳厚度為40%， 而對于8 m高的擋土墻， EPS厚度最佳厚度為20%. 墻體越高， EPS厚度可適當減小， 這樣有利于減小擋土墻的正向旋轉. EPS厚度達到最佳厚度時， 相同地震強度作用下， 其側向應變越大， 右側的土體的抗剪強度得到有效發揮， 達到主動土壓力狀態， 減小了到達墻背的土壓力. 而繼續增大厚度時， 地震能量增量的隔離已達到最大限度， 繼續增加緩沖層厚度反而對擋土墻的抗轉動不利.

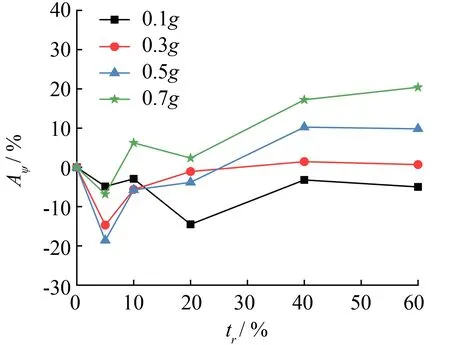
(a)擋土墻高4 m

3.3 EPS緩沖層對側向地震推力增量的影響

振源頻率為3 Hz， 采用0.1g、 0.3g、 0.5g和0.7g不同激勵強度的正弦加速度信號， 分別計算設置EPS歸一化厚度為5%、 10%、 20%、 40%和60%的工況墻體中部參考點的水平推力增量與沒有EPS時工況的水平推力增量. 利用公式(1)計算出水平推力增量的隔離效率值Ap. 圖6是4、 8 m高的墻體墻體的水平推力增量Ap與EPS厚度tr之間的關系之間的關系. 圖7是歸一化厚度最佳時， 兩種高度墻體的側向土壓力值沿墻體高度的變化.

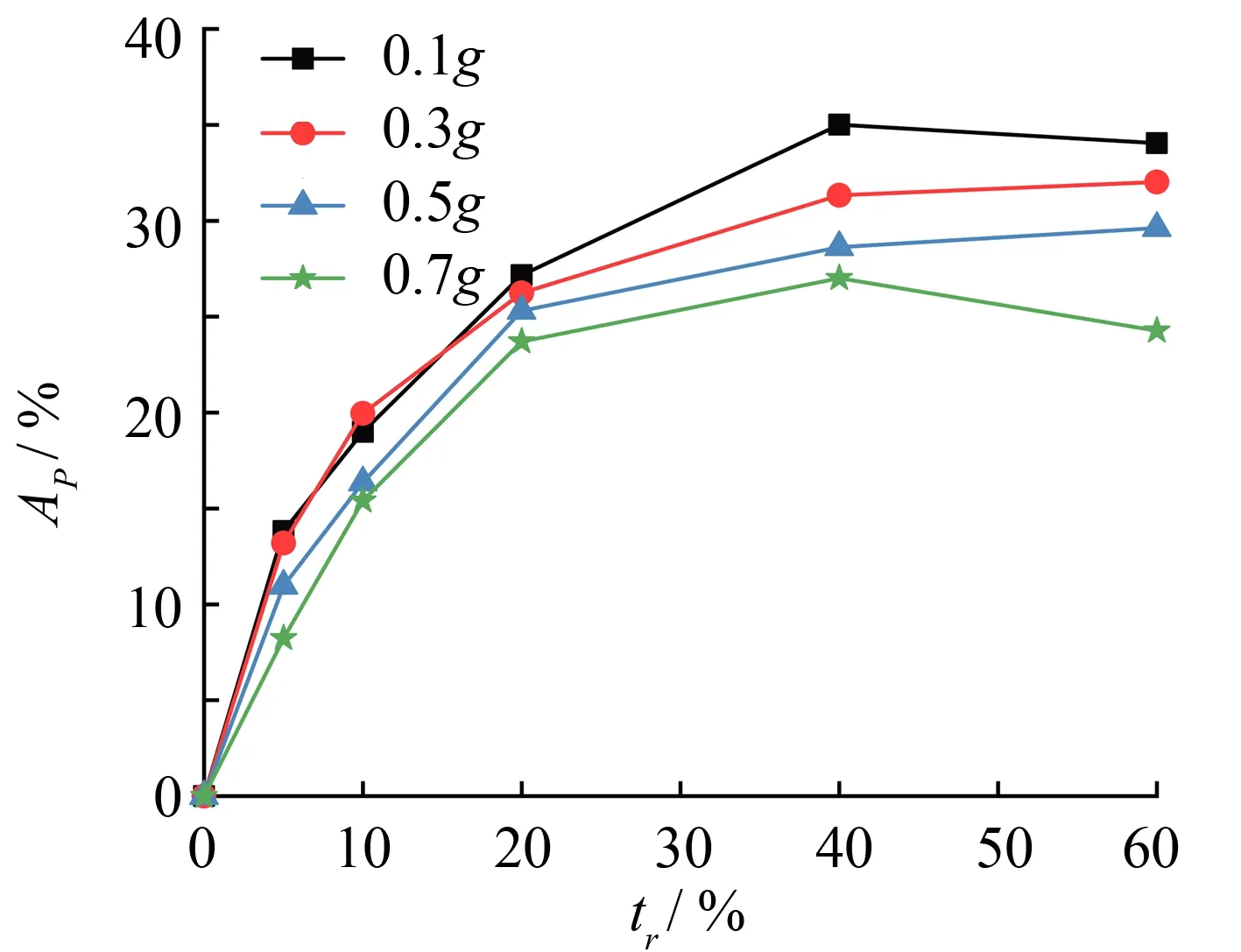
(a)擋土墻高4 m

由圖6(a)可知， 隔離效率隨緩沖層厚度的增加而增加， 但tr達到40%時， 不同激勵強度時AP基本達到峰值， 并且Ap隨著激勵強度的增加而有小幅度降低. 由圖6(b)可知， 對于8 m墻體，Ap隨著厚度的增加而增加， 直至達到25% ～ 35%的峰值范圍， 即使tr再增加，Ap也不會超過這個最大值. 因此， 對于4 m高的擋土墻， EPS的歸一化厚度在40%左右和小振動強度時， 緩沖層能起到最優的隔離水平地震推力的效果； 而對于8 m高的擋土墻， EPS厚度最佳厚度為20%.

在輸入激勵強度0.5g、 激勵頻率3 Hz， 無EPS和EPS厚度40%的兩種工況下， 得出的4 m高墻體側向土壓力隨墻體頂部到底部歸一化墻高(分析高度和墻高的比值)的變化， 如圖7(a)所示. 在輸入激勵強度為0.5g、 激勵頻率為3 Hz， 無EPS和EPS厚度為20%的兩種工況下， 得出的8 m高墻體側向土壓力隨墻體頂部到底部歸一化墻高的變化， 如圖7(b)所示. 由圖7可知， 設置EPS緩沖層導致沿大部分墻體高度的土壓力減少. 設置一定厚度的EPS緩沖層后， 在地震作用下， 傳遞向上層回填土的地震能量被緩沖層反射和吸收， 且右側回填土的抗剪強度得到了有效發揮， 達到主動土壓力狀態， 從而減小了墻背土壓力.

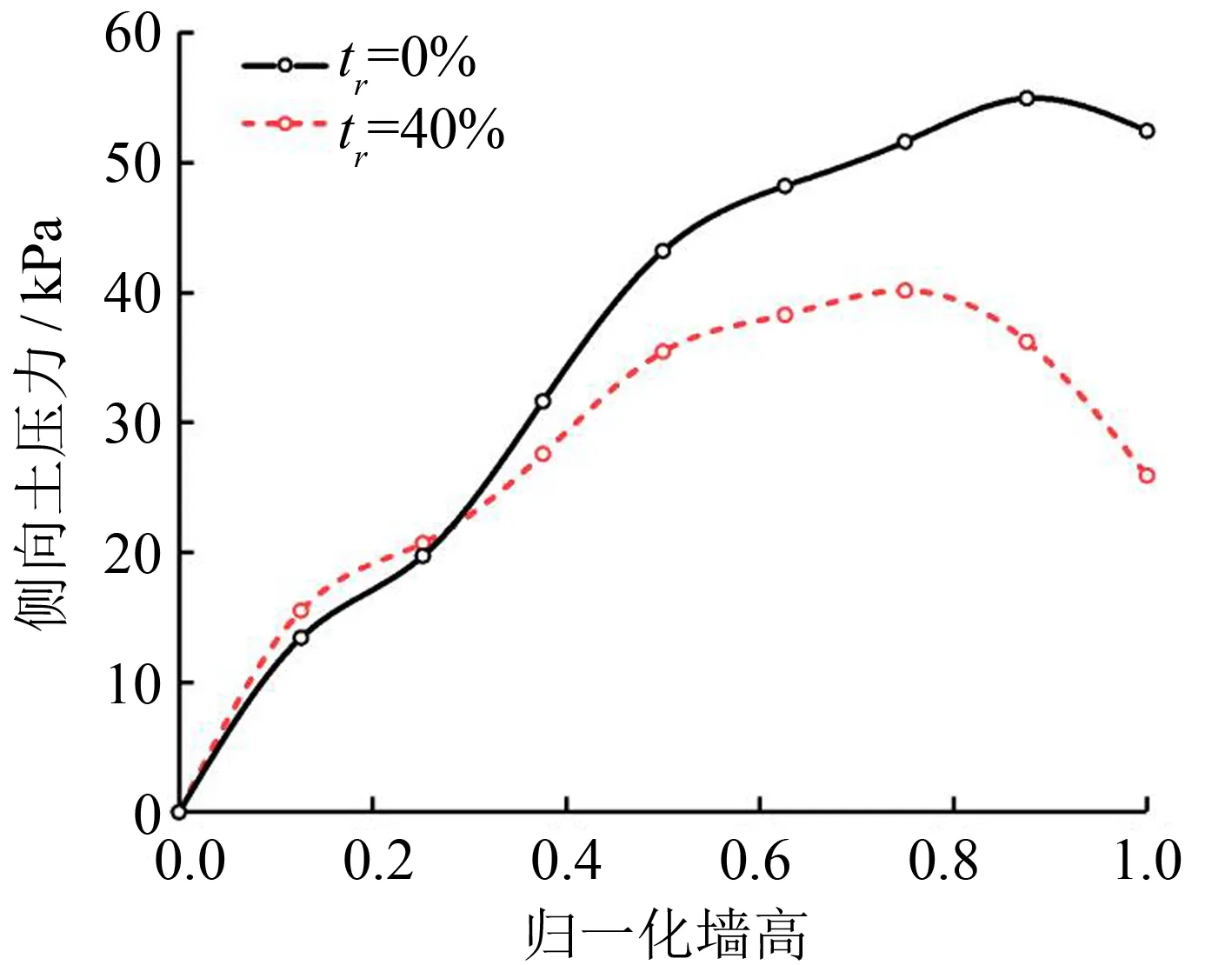
(a)擋土墻高4 m

4 結語

1) EPS材料是一種經濟、 隔離振動效果好的緩沖層， 可以減少新的或現有地震加固的重力式擋土墻結構的永久地震位移和側向推力增量.

2) 地震位移增量、 墻體轉角和側向推力增量隨著EPS緩沖層的相對厚度的增加而增加， 對于高度較低的擋土墻， EPS厚度為墻高40%左右隔離效率接近一個極限值， 此時隔離效率達到最優； 而對于高度較高的擋土墻， EPS厚度為墻高20%左右隔離效率達到最優， 并且設置EPS緩沖層顯著減小了墻體的側向土壓力.