雙旋彈非線性角運動特性分析
李佳訊,沈元川, 賈振岳,于劍橋
(1 北京理工大學,北京 100081;2 北京電子工程總體研究所,北京 100854)
0 引言
針對旋轉穩定彈丸高轉速的特點,通過采用鴨舵組件代替原有引信構成“雙旋”結構實現對旋轉穩定彈智能化、靈巧化改造已經成為該領域的強烈共識。雙旋彈動力學具有強耦合、強非線性的特點,同時結構的變化與控制系統的引入使得彈丸的諸多非線性運動現象難以用線性系統理論分析和解釋,因此對雙旋彈開展非線性動力學分析具有重要的理論意義與工程應用價值。
雙旋彈在飛行過程中有時會出現攻角大小不衰減的圓錐擺動,使得彈丸射程減小,甚至導致運動出現失穩。對于旋轉彈的角運動特性分析,一般借助美國著名外彈道學者Murphy針對彈箭建立的角運動方程[1-2]。韓子鵬對彈箭的圓錐運動以及非線性角運動特性開展了深入的研究,發表了多篇學術著作[3-4]。常思江等對雙旋彈前體周期性干擾引起的強迫運動進行了研究,得到了周期性舵控作用強迫項對應特解的表達式,并對前體轉速閉鎖問題進行了初步分析[5]。舒敬榮等研究了非線性力矩作用下氣動偏心的低速旋轉彈丸的強迫圓錐運動的穩定性條件[6]。
在彈道的非水平段,當偏航舵偏轉到一定程度時,雙旋彈角運動會產生動態失穩的現象,這種現象是雙旋彈動力學分岔造成的。分岔分析是研究非線性動力學系統復雜運動行為,掌握解的拓撲結構與系統參數之間關系的一種手段,在飛行器工程領域取得了許多有價值的研究成果。Carroll等采用分岔分析方法研究了大攻角下飛行器的動力學問題[7]。許多生等提出了一種快速有效的研究方法,對飛機滾轉時的慣性耦合運動進行了分岔分析和穩定性分析[8]。Gill等對標準飛行包線外的飛行器控制器特性進行了分岔分析,研究了系統穩定性與控制器參數的關系[9]。鐘揚威等研究了彈箭角運動的霍普夫分岔現象,分析了飛行高度對極限環擺幅的影響[10]。
文中根據雙旋彈非線性角運動方程組,從氣動非線性和幾何非線性兩個角度分別研究了雙旋彈典型的非線性運動特性。給出了基于平均法的角運動擬線性分析方法,以及基于中心流行定理的角運動分岔分析方法。結合某型雙旋彈參數,得到了三次方靜力矩作用下雙旋彈產生穩定圓錐擺動的必要條件,同時分析了以偏航舵偏角為分岔參數的雙旋彈非線性角運動分岔特性。最后通過數值仿真,驗證了分析方法和結果的正確性。
1 雙旋彈非線性角運動方程
對于雙旋彈的角運動,可以認為雙旋彈速度V、轉速ωx為慢變量,故選取x=[αβωzωy]T為雙旋彈非線性角運動的狀態。同時假設雙旋彈穩定飛行過程中α、β為小量,即sinα≈α,sinβ≈β,cosα≈1,cosβ≈1,且小量的乘積為0。進一步,忽略馬格努斯力以及舵面控制力對雙旋彈角運動的影響。根據雙旋彈的運動方程組,可以推導非線性角運動方程為:
(1)
式中:
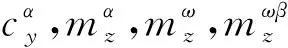
2 氣動非線性下角運動特性分析
2.1 雙旋彈角運動振幅平面方程
在討論氣動非線性對雙旋彈角運動的影響時,可以引入水平彈道假設,即?= 0°。采用Murphy穩定性理論中的復數分析方法,定義復數變量Δ=β+iα和δ=δy+iδz,從式(1)中消去ωz、ωy及其導數,可以得到雙旋彈的非線性復攻角方程:
(2)
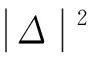
(3)
設式(3)的解具有二圓運動的形式:
Δ=K1eiφ1+K2eiφ2
(4)
定義阻尼因子λi:
(5)
將式(4)、式(5)代入式(3)得:
(6)

(7)
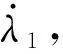
(8)
(9)
(10)
同理可以得到:
(11)
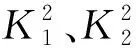
(12)
2.2 圓錐運動穩定條件
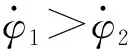
(13)
(14)
需要注意的是,λ1和λ2表達式有意義需要滿足:
(15)
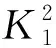
(16)
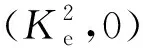
(17)
(18)
綜合式(15)、式(17),由李雅普諾夫判據可知,雙旋彈存在穩定的圓錐運動的必要條件為:
(19)
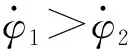
(20)
式中:

綜上所述,式(19)、式(20)構成了雙旋彈在三次方靜力矩作用下產生穩定圓錐運動的必要條件。
2.3 仿真驗證
為驗證上述結論的合理性,選取不同氣動參數組合進行數值仿真,如表1所示。

表1 氣動參數表
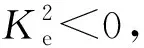
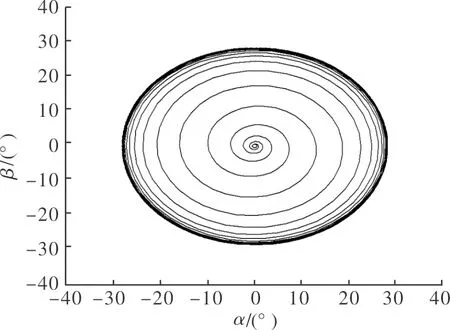
圖1 算例1中初始狀態在極限環內的相軌
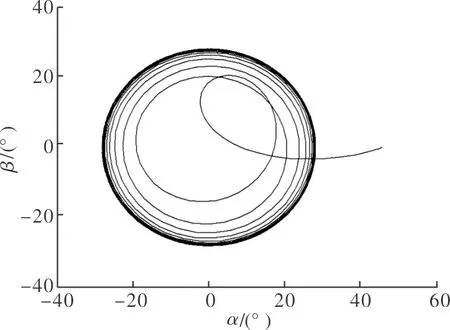
圖2 算例1中初始狀態在極限環外的相軌
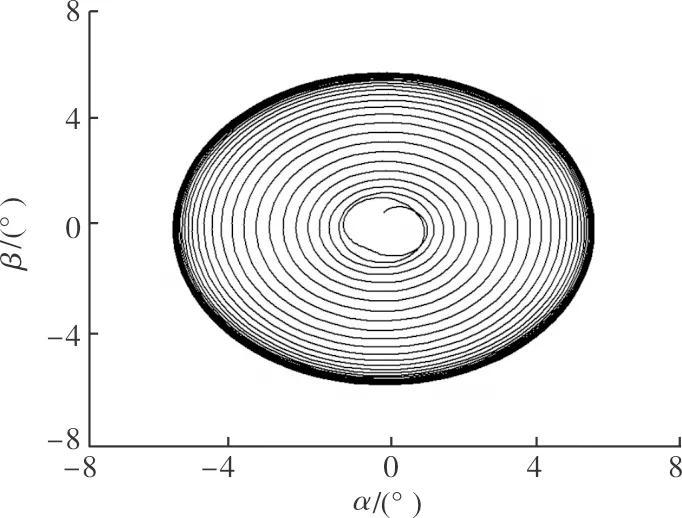
圖3 算例2中初始狀態在極限環內的相軌
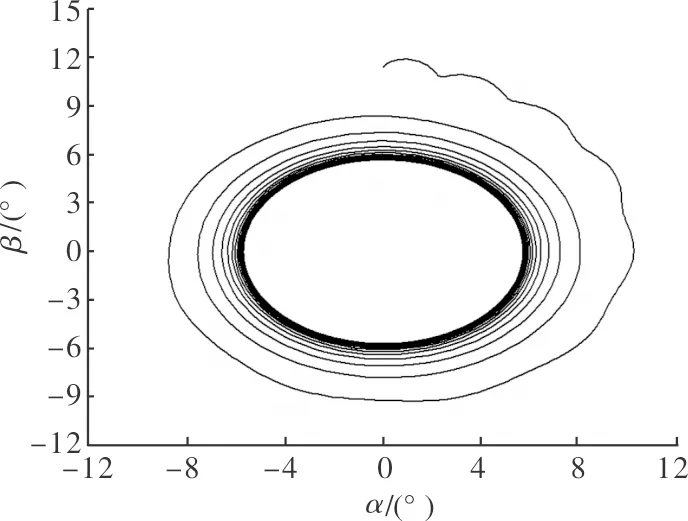
圖4 算例2中初始狀態在極限環外的相軌
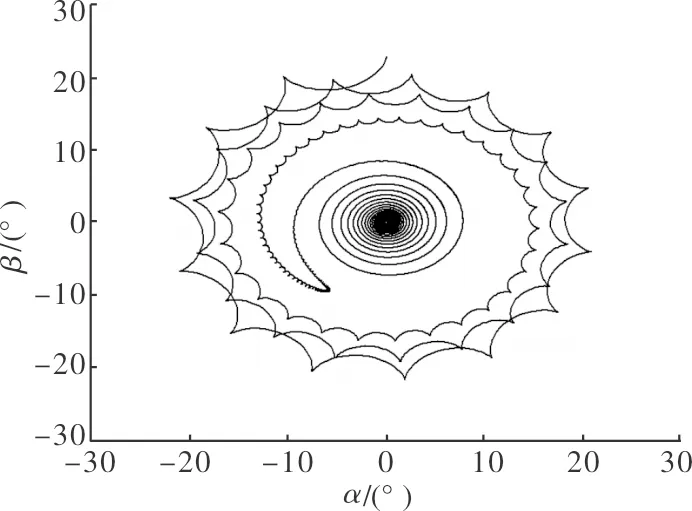
圖5 算例3中相軌
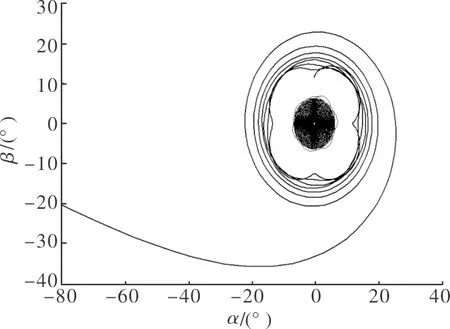
圖6 算例4中相軌
3 幾何非線性下角運動特性分析
3.1 角運動穩定邊界條件
設γ=[δyδz]T是含參非線性系統式(1)的參變量,設系統的平衡狀態為xe(γ)=[αeβeωzeωye]T,則系統在平衡狀態的雅克比矩陣為:
(21)
對應的四階特征方程可以表示為:
s4+p1s3+p2s2+p3s+p4=0
(22)
對于穩定飛行的雙旋彈,ωze、ωye的數值非常小,取ωze≈0,ωye≈0,并做mΔ≈M,mω≈PT的近似處理,則式(22)中特征方程系數表達式為:
(23)
若忽略αe,并令HPT-PM=Q,根據四階勞斯-霍爾維茨判據,系統在平衡狀態穩定的充要條件為特征方程式(22)的系數滿足如下條件:
(24)
將式(23)代入式(24)可以得到關于βetan?的二次不等式:
r1(βetan?)2+r2(βetan?)+r3<0
(25)
其中多項式系數滿足:
(26)
對于雙旋彈一般有M>>HT,則可由式(25)得到系統穩定時βetan?需要滿足的邊界條件為:
β1<βetan?<β2
(27)
式中:
由式(27)可以得到系統穩定時δy需要滿足的邊界條件為:
(28)
式中:
3.2 分岔特性分析
在臨界點處,系統平衡狀態穩定性發生了突變,其動力學發生了分岔現象,下面對雙旋彈的分岔性態進行計算分析。
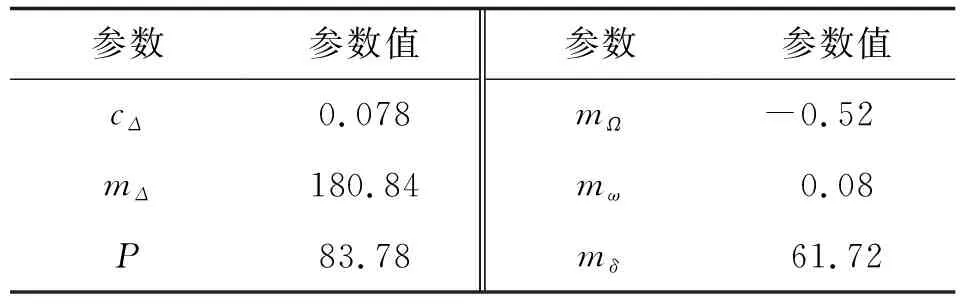
表2 氣動參數表
考慮?=-45°,以δy為分岔參數μ,使用x1,x2,x3,x4表示系統的狀態,將表2的氣動參數代入角運動方程式(1)中,得到含參非線性系統:
(29)
使用式(28)的結論,可以驗證當μ=μ0=0.2時,系統穩定性發生突變,此時系統的平衡點與雅克比矩陣特征值如表3所示。在此平衡點處,特征值為兩對共軛復數,一對特征值具有負實部,另一對特征值實部為零。根據霍普夫分岔定理[11],該平衡點為系統的一個霍普夫分岔點,且系統在分岔點附近將會產生極限環。下面將對系統在分岔點附近的運動特性進行深入分析。
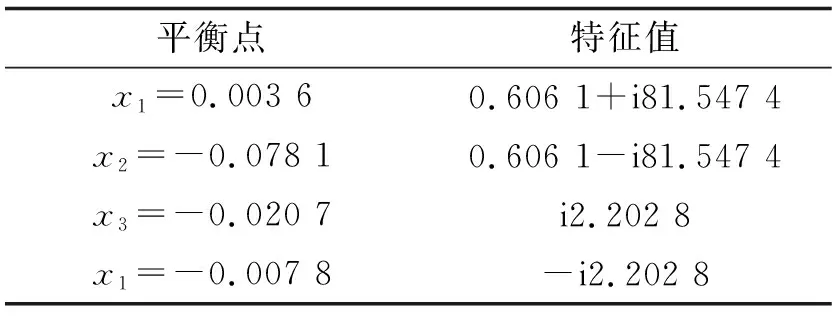
表3 系統平衡點和雅克比矩陣特征值
不失一般性,在分岔點附近將平衡點擬合為分岔參數μ的線性函數,將系統的原點移至平衡點,并令μ=λ+μ0,則雙旋彈角運動方程在分岔點附近可以等價描述為:
(30)
根據文獻[12]中心流行定理的計算方法,取非奇異線性變換矩陣B為表3每對共軛特征值所對應的一個特征向量的實部與虛部構成的方陣,如式(31)所示。

(31)
做非奇異變換x=By,系統式(30)可以變換為:
(32)
其中G(y,λ)為系統的非線性項。根據中心流行定理,系統式(32)過霍普夫分岔點(0, 0)有二維穩定流行和中心流行,可以計算出二維中心流行為:
(33)
其中H.O.T表示3階以上的高階項。
將式(33)代入式(32)中可以得到原系統降維后的二維約化方程:
(34)
根據中心流行定理,原系統在霍普夫分岔點附近的運動特性可通過分析約化方程式(34)來確定。
令y1=rcosθ,y2=rsinθ,將約化方程式(34)在極坐標下寫成規范形形式:
(35)
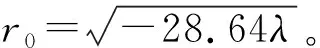
3.3 仿真驗證
為了驗證上述結論的有效性,將式(27)、式(28)計算結果與Matcont數值仿真結果進行對比。當?=45°時,由式(27)、式(28)可以得到雙旋彈角運動穩定時βe所需要滿足的邊界條件為-26.6°<βe< 2.3°,對應的,δy所需要滿足的邊界條件為-8.5°<δy< 76.4°;當?=-45°時,由式(27)、式(28)可以得到雙旋彈角運動穩定時βe所需要滿足的邊界條件為-4.5°<βe< 26.5°,對應的,δy所需要滿足的邊界條件為-79.5°<δy< 11.5°。
Matcont數值仿真結果如圖7、圖8所示。圖7為?= 45°時,平衡攻角、側滑角隨δy變化的曲線,l1,k1段對應的為不穩定的平衡攻角、側滑角,l2,k2段對應的為穩定的平衡攻角、側滑角,當δy=-8.8°時系統的平衡狀態屬性發生了突變,對應圖中H1點,此時αe=-0.07°,βe=2.4°;圖8為?=-45°時的分岔圖,l3,k3段對應的為穩定的平衡攻角、側滑角,l4,k4段對應的為不穩定的平衡攻角、側滑角,當δy=13.5°時系統的平衡狀態屬性發生了突變,對應圖中H2點,此時αe=0.2°,βe=-4.9°。數值仿真得到系統失穩邊界的βe,δy與式(27)和式(28)計算得到的穩定邊界基本一致,表明穩定邊界條件可以作為偏航舵偏角引起雙旋彈在非水平彈道處動態失穩的判定依據。
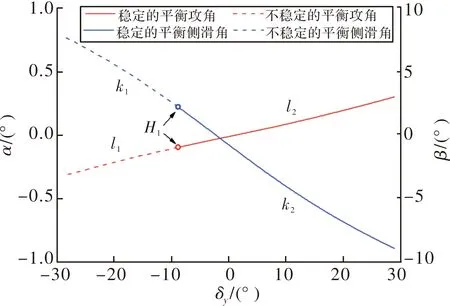
圖7 ?=45°時以δy為分岔參數的分岔圖

圖8 ?=-45°時以δy為分岔參數的分岔圖
為驗證式(35)描述的系統在分岔點附近的運動特性,使用Matcont對系統的分岔現象進行了數值仿真計算,系統平衡狀態αe,βe隨分岔參數δy的變化如圖9所示。隨著δy的變化,系統在δy,0處產生了霍普夫分岔,系統的平衡狀態由穩定的平衡點突變為不穩定的平衡點,并在穩定平衡點一側產生不穩定極限環,極限環的幅值隨著|δy-δy,0|增大而增大。數值仿真結果與理論分析結論一致,表明上述分岔分析方法能夠準確描述雙旋彈的角運動特性。
4 結論
根據雙旋彈的非線性角運動方程,從氣動非線性和幾何非線性兩個方面對雙旋彈非線性運動特性進行了分析,結論為:
1)三次方非線性靜力矩作用下的雙旋彈,在滿足式(19)、式(20)所確定的約束條件時,其角運動能夠產生穩定的圓錐運動,此時雙旋彈攻角不衰減,會影響彈丸的射程,甚至導致飛行失穩,對于雙旋彈的結構、氣動設計具有指導意義。
2)當雙旋彈的彈道不平直時,且當偏航舵偏角增大到一定程度時,產生的頭部側向控制力會導致角運動動態失穩。在臨界點處動力學發生了霍普夫分岔現象,越過分岔點穩定的平衡狀態消失,而在穩定分岔點一側產生了不穩定的極限環。控制方案的設計過程應避免使雙旋彈角運動進入不穩定極限環與不穩定平衡點的吸引域。

