基于ESO的小型飛行器增量動態逆控制律設計
高少婷
(中國飛行試驗研究院,西安 710089)
0 引言
隨著低成本、輕便型微處理器和慣性測量元件廣泛使用,小型飛行器也越來越受到歡迎。
對于小型飛行器來說,由于傳感器的約束,獲取準確的模型要付出很大的代價、甚至是不可能的,并且往往具有較強的非線性特性。所以,小型飛行器的控制系統必須在提供強魯棒性的同時能夠解決它的非線性問題。文獻[1]通過將神經網絡與動態逆方法相結合,從而克服動態逆方法對精確模型的依賴性。文獻[2]在采用動態逆方法的基礎上,利用自適應方法對建模誤差進行補償。但是這些方法多是將動態逆方法與智能控制理論或自適應控制理論相結合,設計過程復雜。文獻[3]提出了基于角加速度反饋的動態逆控制方法,該方法將飛行器的控制方程寫成增量的形式,以角加速度作為控制反饋,舵面偏轉增量作為控制量,降低了控制器對系統模型的依賴性。文獻[4]提出了帶有跟蹤微分器的增量動態逆控制律設計方法,通過跟蹤微分器得到狀態速率信息。文獻[5]通過在控制器中引入預測濾波器,實現對角加速度的濾波和預測。
文中首先建立了小型飛行器的縱向平面的非線性模型,然后設計增量動態逆姿態控制器,引入擴張狀態觀測器得到控制器所需的狀態速率,解決了狀態速率難以測量的問題。最后通過MATLAB/Simulink仿真驗證控制器的性能。
1 模型描述
采用某小型飛行器模型進行仿真計算,姿態動力學方程如式(1)所示。
(1)
姿態運動學方程如式(2)所示。
(2)
其中,?,ψ,γ為飛行器在空間飛行時的俯仰角、偏航角和滾轉角。
2 增量動態逆控制
為了方便描述增量動態逆控制,考慮如下仿射非線性系統:
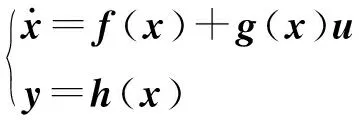
(3)
式中:x為n維狀態向量;控制輸入u和系統輸出y皆為m維向量;f和h分別為n階和m階矩陣;g為一個n×m的控制矩陣。
在(x0,u0)的某個領域內對上述系統進行一階泰勒展開,即
(4)
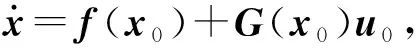
(5)
當控制器采樣頻率很高,控制計算的周期足夠小時,假設控制輸入u的變化速率快于狀態變量x。考慮到這項因素,最終可化簡為:
(6)
則系統輸出的動態方程可寫為:
(7)
(8)
在實際應用中,采用式(9)。
v=K(yc-y)
(9)
其中yc為系統的期望輸出;y為系統的實際輸出;K為待設計的系統帶寬。
3 小型飛行器增量動態逆控制算法設計
3.1 姿態回路增量動態逆控制
依據動力學模型,基于增量動態逆控制算法對小型飛行器的姿態回路設計控制器,將式(1)寫成狀態方程的形式:
(10)
其中,將飛行器所受合外力矩分解為兩個部分:1)由飛行器的空氣動力系數和飛行狀態所產生的力矩Ma;2)由執行機構舵面所產生的控制力矩Mc。將系統的姿態控制方程(10)寫成如式(3)所示的形式,即
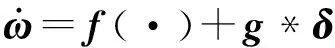
(11)
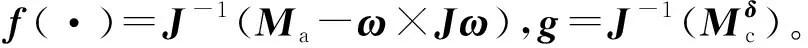
由式(11)求得姿態回路的控制輸入增量形式為:
(12)
v=K2(ωc-ω)
(13)
式中,K2為角速度控制回路帶寬。
小型飛行器角回路采用線性控制器,表達式為:
ωc=K1(φc-φ)
(14)
具體的姿態控制回路的結構如圖1所示。
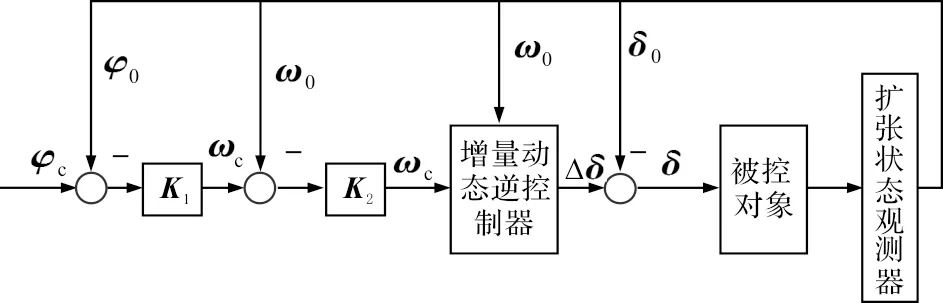
圖1 小型飛行器姿態控制結構圖
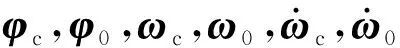
3.2 魯棒性分析及控制參數設計
由于小型飛行器動力學模型存在不確定性和未建模動態,所以需要分析所設計控制器的魯棒性。
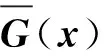
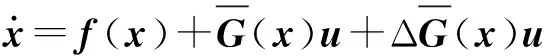
(15)
依據前文所述,系統方程可簡化為:
(16)
將增量動態逆控制律代入式(16),可得
(17)
對于小型飛行器姿態角速度回路來說,式(17)可寫為:
(18)
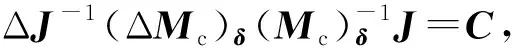
(19)
由此可以得到角速度控制回路的閉環系統結構如圖2所示,通過計算得到角速度回路的相應閉環傳遞函數如式(20),從中可以看出,系統中的不確定性被消除。
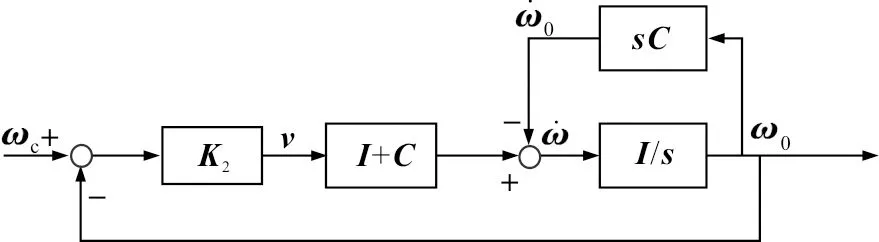
圖2 小型飛行器角速度閉環結構框圖
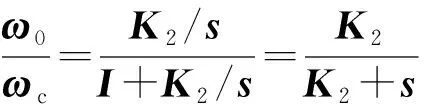
(20)
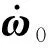
(1984年1月6日講座,全文略有刪節。吳培華教授提供講座錄音,史悠整理,劉祥安教授審閱,在此特申謝忱!)
以俯仰角控制為例,研究控制參數的設計。由式(21)可知俯仰角速度回路閉環傳函為k2/(k2+s),因此簡化后的俯仰角控制回路的閉環系統結構圖如圖3所示。
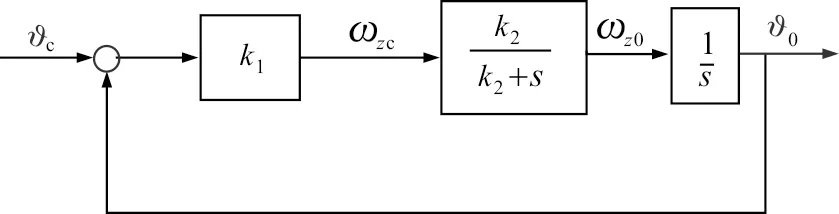
圖3 小型飛行器俯仰姿態閉環結構框圖
在此基礎上,對于俯仰角控制系統的整個閉環回路傳遞函數可表示為:
(21)
標準的二階系統傳遞函數形式為:
(22)
因此,可以得到下面的表達式:
(23)
為使系統具有較好的閉環特性,取ξ=1,ωn=20,由此計算得到:
k1=10,k2=40
(24)
3.3 角加速度的獲取
通過陀螺儀測量可以得到飛行器的角速度,若是通過微分的方式得到角加速度,則獲得的角加速度信息噪聲過大,所以文中提出了一種通過擴張狀態觀測器估計角加速度信息的方法。具體形式為:
(25)
式中:z1為對角速度的估計值;z2為對角加速度的估計值;βi為觀測器的控制系數。其中非線性函數fal表達式為:
(26)
4 仿真結果與分析
由文中所設計的增量式動態逆控制器和小型飛行器縱向動力學模型,在MATLAB仿真環境驗證所設計的控制系統的性能。要求飛行器作無側滑無傾斜的運動。初始狀態為:俯仰角?=0°,速度V=25 m/s。對控制參數進行設計,增量動態逆控制器的設計參數為:k1=10,k2=40;擴張狀態觀測器控制參數為λ=0.5,α=0.5,β1=200,β2=300;輸入指令周期為4 s,0°~5°為跳變的俯仰角指令,仿真結果如圖4所示。
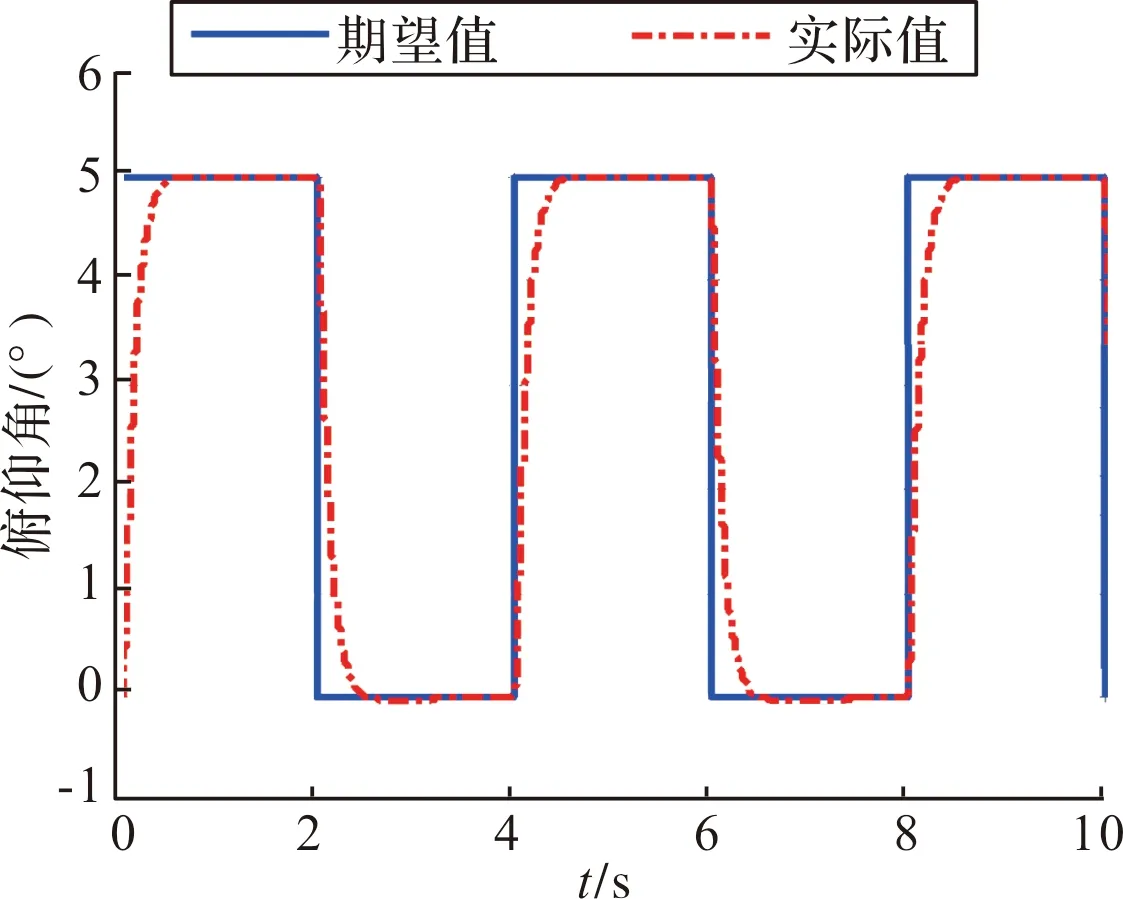
圖4 俯仰角跟蹤曲線
從以上仿真結果可以看出,在無攝動無干擾的情況下,系統的響應時間約為0.4 s,響應較快,具有很好的快速性,幾乎無超調,具有良好的控制效果,證明所設計的的增量動態逆控制能夠實現小型飛行器的姿態控制,且動態性能良好。
因為小型飛行器的氣動參數具有不確定性,為驗證所設計控制器的魯棒性,在仿真中將氣動參數拉偏30%,觀察參數攝動影響下控制器的性能效果。

圖5 氣動參數拉偏30%俯仰角跟蹤曲線
由圖5可知,在加入氣動參數攝動之后控制器仍能實現小型飛行器的姿態穩定跟蹤,并且具有良好的快速性,從而驗證了控制系統的魯棒性。
5 結論
針對小型飛行器氣動參數不確定性的問題,設計了基于擴張狀態觀測器的增量動態逆控制方法。通過角加速度的引入降低了控制系統對飛行器氣動參數不確定性的敏感度。通過擴張狀態觀測器實時估計角加速度信息,解決了角加速度無法直接測量的困難。仿真結果表明,當飛行器精確模型難以建立,存在參數攝動時,所設計的方法具有較好的魯棒性。

