多孔介質兩相流耦合地應力問題的非線性混合有限元方法

劉子平, 李俊翔, 劉 琦, 馬 強, 魏華祎

(1. 中國石油川慶鉆探工程有限公司，成都 610051; 2. 四川大學數學學院，成都 610064;3. 湘潭大學數學與計算科學學院，湘潭 411105)

0 引言

在石油工程中，油藏模擬器是描述油藏中復雜流動機理的工具，大多數石油與天然氣公司都使用油藏模擬器來設計與預測石油或者天然氣的產出與效果。我國蘊藏著豐富的頁巖氣資源，其大規模開發將是我國滿足天然氣需求的重要途徑和保障，但相對于傳統油氣資源，人們對于頁巖氣開采中流體流動機理認識還不是很成熟，而數值模擬是研究頁巖氣藏流動機理的重要手段，目前相關的數值模擬算法和軟件與國外還有很大差距。

大多數模擬器都關注于孔隙介質中的流動過程，而結構本身的地應力則沒有得到相對應的關注。事實上，多孔介質是可變形的，需要我們考慮流體流動與巖石變形之間的相互作用。在常規的固化巖石儲層中，我們可以調整流動方程來充分描述地質結構中的低孔隙壓縮性，剛度過載以及輕微的壓降。但在非常規儲層比如頁巖氣的開發中，非固化的介質、大的壓降以及水力裂縫使得流動與結構變形之間的相互依賴與相互作用變得顯著[?,?,?,?]，從而必須對此現象進行顯式地描述。這就需要我們建立流動與地應力相互耦合的數學模型并發展相應的數值計算方法來分析此類復雜問題。

在進行數值模擬中，大多數油藏系統都是非均勻的，它們由其流動性質上的空間變化來刻畫，比如滲透率需要使用二階張量進行描述。為此，在模擬中，我們有必要獲得非常精確的速度分布，因為流體的流動路徑將由速度方向決定。此外，得到關于飽和度解的準確描述也總是需要的。在石油工程數值模擬中，常常使用有限體積法或者單元中心有限差分離散來描述非變形的多孔介質，因為這些方法可以保證局部的質量守恒[?]，而對于描述固體的變形，有限元方法則是更好的選擇[6–7]。混合有限元方法通過將質量守恒方程與達西定律方程同時進行求解，既能滿足局部的質量守恒也可以給出速度場更加精確與連續的描述[?,?,?]。由此，混合有限元方法也在描述多孔介質中的流動與巖體形變的耦合中得到了大量的使用[?,?,?,?,?,?,?,?,?,?]。

本文針對頁巖氣勘探開發過程中水氣或水油兩相流耦合的地應力計算與模擬問題展開研究，構建地質孔隙結構非線性兩相流耦合地應力數學模型，提出合理的離散數值計算格式，構建相應的非線性混合有限元算法，并針對典型的兩相流地應力問題進行計算模擬。

1 控制方程

為模擬帶裂縫儲層中的孔隙應力問題，孔隙介質中的流體流動與地應力產生了耦合，而地應力導致了巖石結構的線彈性變形。流體的流動與結構的應力應變充分耦合，需要在統一的系統下進行求解以保證精度與數值穩定性。一般地，我們首先推導兩相流作用下的地應力耦合模型，基于兩相流的質量守恒方程為

2 混合有限元分析與算法

下面對耦合地應力模型構建有限元算法，令未知量S0、vt、p、u分別屬于函數空間

注意這里vini= 0 下標i為坐標分量求和，并非流體標識0 與1，表示在邊界上法向速度的約束，即邊界沒有流體流出。由(??)，可得到問題的弱形式為

其中σt=bp0I+σ0+σeff，(·,·)Ω表示區域Ω上內積，〈·,·〉Γ2表示邊界Γ2上內積，測試函數

注意到左端整體矩陣中的子矩陣包含了未知量，并且右端項也包含了非知量。為簡單起見，我們采用固定點迭代計算求解該非線性問題。由此建立有限元計算流程如下：

3 數值算例與討論

3.1 無裂縫水驅油模型

下面給出數值算例，首先我們考慮一個均勻無裂縫區域下的水驅油兩相流地應力模型。設模型中0 表示水相，1 表示油相，區域Ω=[0,10]2m2由32×32×2 的一致三角形單元離散，如圖1 所示。

圖1 正方形無裂縫巖石區域，使用三角形對區域作離散

表1 為巖石，水與油的材料參數，其中λ表示彈性拉梅第一常數，μ表示巖石剪切模量，由此可以得到四階彈性系數張量為

表1 巖石與液體參數

C=Cijkl=λδijδkl+μδikδjl+μδilδjk,

圖2 給出了在模擬1 000 天注水后區域中的水飽和度、速度、壓力、速度模量以及地應力模量的分布。圖2(a)中飽和度的分布給出了注入水前端的均勻一致傳播，我們可以看到與注入井相距相同的徑向距離有相同的飽度值。這是因為儲層具有均勻的性質，并且沒有流體流出。圖2(c)中的壓力分布給出了一個在注入井處與產出井處的壓力梯度，速度最高處位于注入井與產出井附近。計算得到的飽和度，壓力，速度解顯示了我們的算法能給出孔隙介質多相流動的準確物理行為。

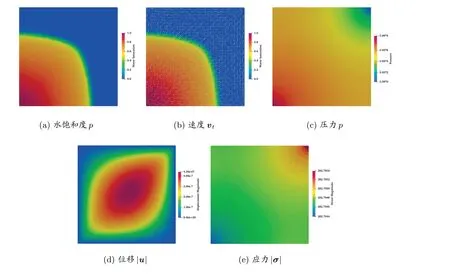
圖2 均勻巖石結構注水1 000 天后的計算解

由于整個結構具有各向同性的彈性剛度，位移解與地應力非常光滑并且依賴于壓力梯度，并且如我們所期望的，位移顯示出關于對角線x=y的對稱性。該模型的計算結果與文獻[11]的結果相符，顯示了我們構造的算法的正確性。

3.2 交叉裂縫水驅油模型

接下來，我們考慮如圖3 所示的非均勻巖石儲層區域。在區域中存在一個交叉裂縫，流體在該裂縫中具有更大的滲透率，設其為其它區域巖石滲透率的3 倍，模型的其它參數仍如表1 保持不變。由于裂縫尺寸較小，我們對區域進行如圖3 所示的非結構化有限元網格剖分。與上節中的條件一樣，我們仍然在左下角進行注水，油在右上角流出。模擬時間設置為152 天。

圖3 交叉裂縫巖石區域以及非結構化有限元網格離散

圖4 給出了在152 天時計算得到的水飽和度、速度、壓力、位移以及地應力解。可以看到，裂縫區域中水的流動速度遠大于在巖石中的流動速度，因此通過在左下角的持續注水，流體迅速沿對角線x=y上的裂縫流動。而在巖石中水的流動也受到影響并有向對角線靠攏的趨勢。而在另外一條裂縫x+y=10 處，水的飽和度與無裂縫區域比較也明顯增加。圖4(b)所示的速度分布明顯顯示出裂縫區域的速度大于無裂縫區域的速度。由于裂縫分布的對稱性，壓力、位移與地應力也呈現出對稱性，并且由于區域的非均勻性，計算得到的解明顯沒有均勻巖石區域的解光滑。

圖4 非均勻交叉裂縫區域注水152 天后的計算解

4 結論與展望

本文建立了考慮裂縫儲層的地應力兩相流耦合模型，推導了地應力模型的非線性混合有限元離散格式，構建了二維非線性有限元計算流程，針對典型的帶裂縫的水驅油模型問題，實現了非線性有限元計算模擬，驗證了算法的正確性與有效性。

本文主要關注于有限元方法的工程應用，所考慮的模型相對較復雜，難以構造比較合適的真解實例，我們也沒有對算法進行理論分析，主要通過檢查計算結果是否符合物理實際做為評價結果正確性的標準。當然，在未來的工作中，我們不但要考慮更實際的三維問題，還要從理論層面對算法進行適當的分析，以期建立本文算法收斂性理論。

關于下一步的工作，一方面針對三維帶裂縫的非均勻儲層區域進行有效的建模，使用自適應有限元網格對區域進行更精細的離散，另一方面希望把適用于多邊形和多面體的非標準有限元應用到該非線性問題的求解當中，并設計更高效穩健的算法和程序。