基于SAP2000的框剪結構抗連續倒塌研究

柯長仁， 姚東浩

(湖北工業大學土木建筑與環境學院， 湖北 武漢 430068)

建筑結構的連續倒塌問題逐漸成為近些年來結構安全研究的重點部分。自1968年發生于英國的Ronan Point公寓的煤氣爆炸引起的連續倒塌事件后， 各國開始重視結構的連續倒塌問題， 并因此制定了相應的設計規范和指南。而在經歷發生于美國1995年Alfred P. Murrah聯邦政府辦公樓和2001年“911”事件紐約世貿大廈等多起嚴重連續倒塌事件后， 結構的抗連續倒塌設計越發受到工程界的重視， 我國學者也開始將目光轉向其中， 成為21世紀以來結構安全問題的研究熱點[1]。相應的， 相關設計規范也進行了改進[2]， 2020年9月26日， 世界上最大的抗連續倒塌實驗更是在我國徐州順利完成。但是當前的研究對高層結構而言可能不太適用， 因為當前國內外大量研究大多以多層框架為主。黃華， 劉伯權等[3]使用SAP2000軟件對鋼筋混凝土框架進行了連續倒塌分析， 針對鋼筋混凝土框架剪力墻結構， SAP2000軟件在其分析的運用較少。陸新征， 任沛琪等[4]在對框架剪力墻結構進行連續倒塌分析時發現：如果結構中部位置布置剪力墻， 且所布置的剪力墻相互連接貫通形成筒狀結構， 在部分剪力墻失效拆除后剩余剪力墻仍具有較強的抗連續倒塌能力。而在角部位置布置L型剪力墻， 若剪力墻部分失效， 結構連續倒塌效率如何變化尚未可知。本文根據中國《混凝土結構設計規范》(GB50010—2010)設計一棟典型24層鋼筋混凝土(RC)框剪結構， 建立其有限元模型， 利用SAP2000中的非線性動力方法對結構進行拆除構件分析以驗算其連續倒塌能力。研究剪力墻為L型并位于角柱附近時， 分別拆除各個類型柱子， 結構的連續倒塌概率如何變化， 拆除剪力墻時， 結構的連續倒塌能力如何， 拆除不同位置剪力墻時， 結構的連續倒塌能力如何。

1 鋼筋混凝土框架-剪力墻模型

1.1 模型設計

根據我國現行的《混凝土結構設計規范》[5]和《建筑抗震設計規范》， 運用PKPM設計軟件來設計框剪結構計算模型。 以某二十四層框剪結構為例(圖1, 圖2), 結構層高一至四層分別為6 m、5 m、 5 m和2.2 m,五至二十四層層高均為3.15 m， 總高度81.2 m， 地處7度抗震設防區域。場地為Ⅱ類， 地震分組第一組， 基本風壓為0.45 kN/m2， 剪力墻與框架抗震等級均為二級。屋面恒載5.5 kN/ m2， 活載2.0 kN / m2， 一至三層恒載5.0 kN/m2， 活載3.5 kN/ m2， 四層恒載3.9 kN / m2， 活載2.5 kN/ m2， 五至二十四層恒載5.5 kN/ m2， 活載2.0 kN/ m2。四周外圍墻：二至三層13.5 kN/ m2， 四至二十四層8.0 kN/ m2。混凝土強度等級及鋼筋牌號如表1所示。模型構件尺寸見文獻[6]。

圖 1 框架-剪力墻結構三維結構圖

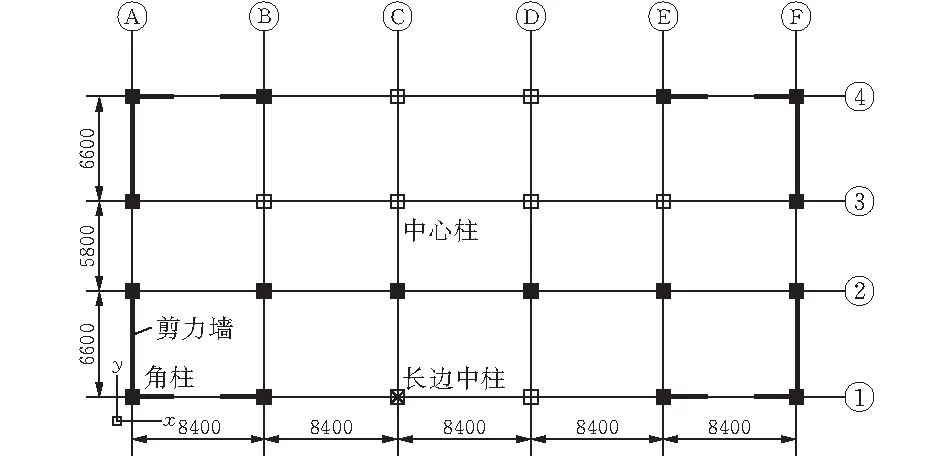
圖 2 結構平面布置圖及構件初始破壞位置

表1 混凝土強度等級及鋼筋牌號

1.2 分析平臺及計算模型

由于對結構的構件進行連續倒塌設計屬于整體力學行為，運用實驗進行研究不太符合實際，因此我們在實際工作中主要運用有限元分析進行研究。在本次研究中使用由美國CSI公司開發研制，迄今為止已有四十多年歷史的商業有限元軟件SAP2000[7]；該軟件具有強大的計算分析功能，并且計算快速、合理，本次研究中我們僅使用其非線性動力分析功能。本文中的框架梁及柱采用線單元，剪力墻采用分層殼單元。為簡化分析，有限元模型中未建立樓板的模型，但是將樓板自重及樓板的荷載等效到相應的支撐梁上，在不考慮樓板的前提下，計算結果偏于安全。

1.3 破壞準則

分析中采用GSA2003[8]規定的荷載組合，即在進行動力分析時，使用式 L=DL+0.25LL。GSA2003中規定非線性分析時采用塑性鉸轉動和位移延性比來衡量，其判定準則為轉角大于6°時認為結構會發生連續倒塌。

1.4 分析方法

在本次研究中為了從整體評價結構的抗連續倒塌能力采用非線性動力拆除構件法對結構進行分析，這是目前可知分析方法中較為準確、使用較為廣泛的方法[9]。該方法在考慮結構幾何非線性與材料非線性的前提下也反映結構的動力響應、P-Δ效應。所以運用此方法來進行分析，不僅可以適用多種結構，更可以使分析數據更加精確。

采用PKPM計算得到結構內力和配筋，將其模型導入SAP2000中，通過非線性動力分析拆除構件法分析框架的抗連續倒塌性能。非線性動力拆除構件分析的基本流程按照DOD2010[10]的規定首先讓結構在重力荷載作用下達到靜力平衡狀態; 然后，在較短時間內迅速拆除目標構件(在有限元模型中瞬間殺死相應單元) ；最后，對結構進行非線性動力分析得出失效點的位移及塑性轉角。本文分別采用拆除底層和十層角柱、長邊中柱、短邊中柱、中心柱以及剪力墻為十種不同的連續倒塌分析工況，每次分析只拆除一種代表構件。

2 框架部分柱失效分析

2.1 拆除不同樓層同一位置構件

塑性轉角均小于規范GSA的限值6°，結構沒有發生連續倒塌破壞(表2)。

圖3a、圖3b所示為首層長邊中柱拆除前后結構整體變化情況，圖3c、圖3d為十層長邊中柱拆除前后結構整體變化情況。可以看出結構長邊中柱拆除后，結構的變形明顯，而且十層長邊中柱拆除后結構變形大于首層拆除長邊中柱后結構變形。

塑性轉角均小于規范GSA的限值6°，結構沒有發生連續倒塌破壞(表3)。

表3 拆除角柱

塑性轉角均小于規范GSA的限值6°，結構沒有發生連續倒塌破壞(表4)。

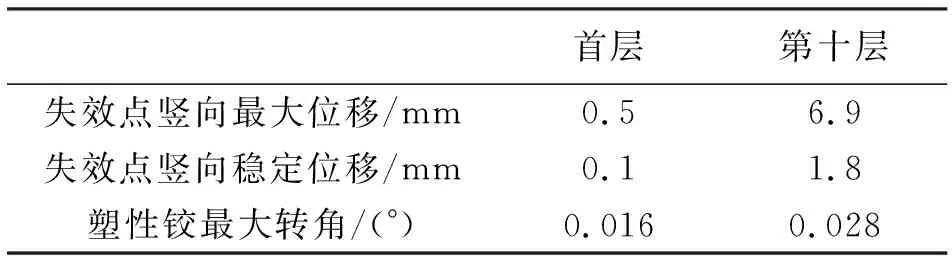
表4 拆除短邊中柱

塑性轉角均小于規范GSA的限值6°，結構沒有發生連續倒塌破壞(表5)。

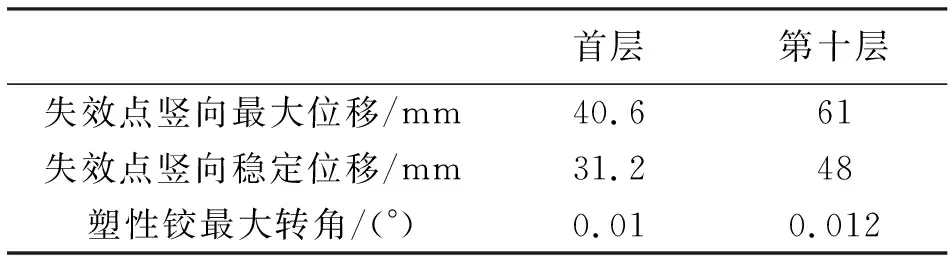
表5 拆除中心柱

由以上分析可知，在角柱與短邊中柱附近設置剪力墻可在該柱失效后明顯降低該柱節點的豎向位移，改善其抗倒塌性能。在拆除本結構任一樓層相同位置典型柱子時，結構均不發生連續倒塌。對于同一建筑同一位置，失效構件所處的層數不同，導致結構連續倒塌的敏感性也不同。以長邊中柱為例，十層失效點豎向最大位移78 mm大于首層失效點最大位移53 mm,豎向穩定位移十層52.8 mm大于首層33.7 mm,塑性鉸最大轉角十層0.074°大于首層 0.057°。同樣的，拆除不同樓層其他同一位置構件，隨著構件所處層數的增高，失效點豎向位移以及塑性鉸轉角相應變大。由此可判斷樓層越高，拆除同一位置構件的連續倒塌概率越大。這是因為底層結構相比于上部結構配筋率更大，使其極限承載能力高于上部結構，除此之外底層柱拆除后，其上部結構超靜定次數相對上部構件失效較大，這些原因導致拆除底層柱后剩余結構仍有較大的冗余度。

2.2 拆除同一樓層不同位置構件(首層)

拆除不同位置柱失效點豎向位移時程曲線對比見圖4，由于短邊中柱豎向位移過小，故在此圖上不多贅述(表6)。由表6可知：

1)首層無論拆除角柱，長邊中柱，短邊中柱還是中心柱，其塑性轉角均小于6°，故根據規范結構不會發生抗連續倒塌破壞。

2)拆除同一樓層不同位置柱構件時失效點最大位移長邊中柱為53 mm>中心柱40.6 mm>角柱1.5 mm>短邊中柱0.5 mm，對于失效點穩定位移同樣是長邊中柱>中心柱>角柱>短邊中柱,對于塑性鉸轉角而言，同樣是長邊中柱0.057°>中心柱0.01°>角柱0.003°>短邊中柱0.0016°。根據GSA2003判定準則為轉角大于6°時認為結構會發生連續倒塌由此得出拆除長邊中柱后此結構發生連續倒塌的概率最大，中心柱次之，之后是角柱，短邊中柱最小。

3)角柱失效后形成懸臂結構承受原結構上部的豎向荷載，理論上來說在上部豎向荷載作用下發生連續倒塌的概率要超過長邊中柱和中間柱，但是由于本結構中角柱失效后與其相連的梁還受到L型剪力墻的約束，其約束力要遠大于長邊中柱和中間柱失效后周圍柱對梁的約束，故角柱失效后結構抗倒塌能力仍然強于長邊中柱和中間柱失效情況。

4)因其承擔荷載小，短邊中柱失效后產生的不平衡荷載也最小，而且在本結構上與其相連的梁同樣受到L型剪力墻的約束。這兩方面原因綜合使短邊中柱就算失效仍具有最強的結構抗倒塌能力。

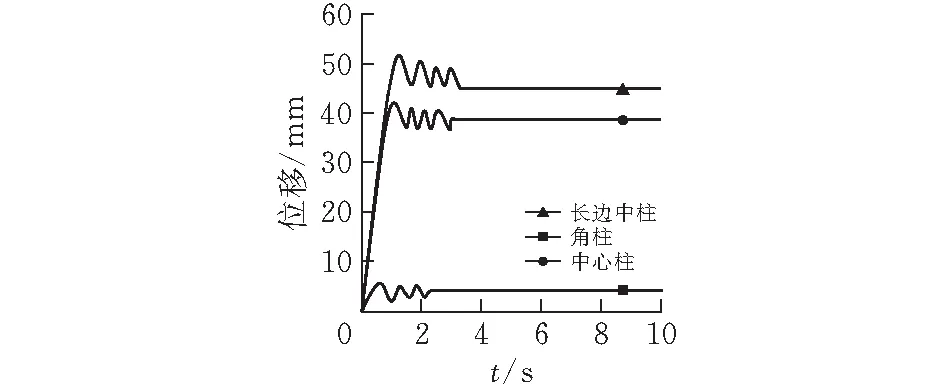
圖 4 拆除不同位置柱失效點豎向位移時程曲線對比

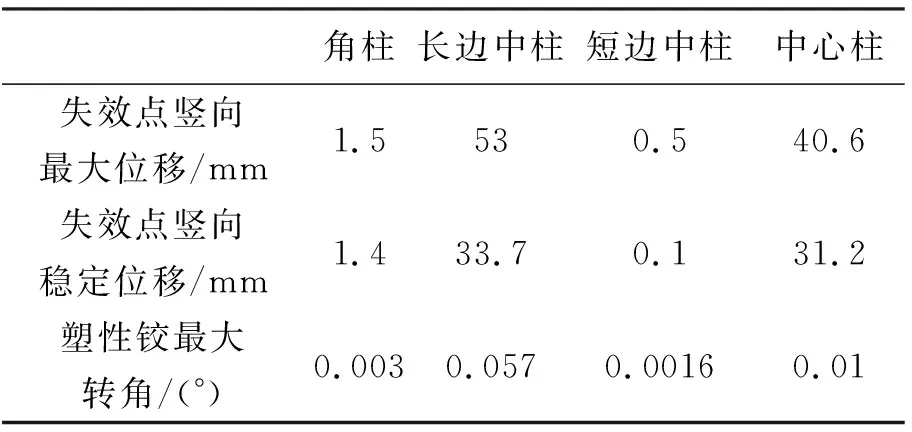
表6 拆除不同位置柱

3 剪力墻部分失效分析

3.1 拆除首層剪力墻Y向

剪力墻拆除位置如圖5所示，位于角柱附近的L型剪力墻，圖6所示為首層L型剪力墻失效后豎向結點位移變化曲線，圖7為其失效后失效點豎向加速度變化曲線，失效后大約0.5 s時結點加速度達到最大的2.5 m·s-2，1.5 s之后加速度逐漸穩定為0.豎向位移達到最大值2.1 mm的時間發生在1.25 s時，從位移變化可以看出位移波動幅度較小，周期也相對較短且不規則，具有較快的衰減速度，其位移穩定在1.5 s時，數值為1.9 mm,這是因為我們將L型剪力墻的Y向拆除后，X向墻體與剩余結構仍然有很好的空間拉結作用，并與Y向失效后剩余墻體相互約束產生較好的抗結構倒塌能力。

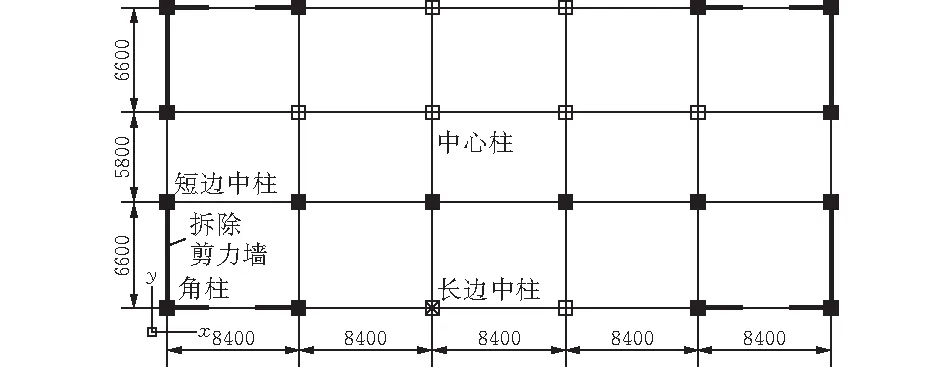
圖 5 被拆除剪力墻示意圖

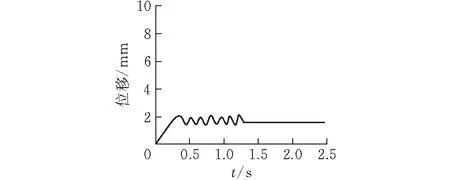
圖 6 首層失效點豎向位移

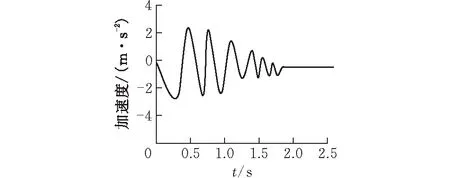
圖 7 首層失效點加速度

3.2 拆除首層與第十層同一位置剪力墻

表7所示分別為首層與十層L型剪力墻失效后結點豎向位移值和塑性鉸最大轉角，圖8所示為不同樓層同一位置剪力墻失效后豎向結點位移變化曲線，圖9為其失效后失效點豎向加速度變化曲線，由表7可以看到，十層的豎向節點最大位移為7 mm，豎向穩定位移為6.9 mm，明顯大于首層的節點最大位移2.1 mm與穩定位移1.9 mm，塑性轉角十層也明顯大于首層，由圖9可以看出豎向加速度明顯高于首層節點位移和加速度，根據判斷準則可以知道失效構件所在層數的高度與結構動力反映的劇烈程度成正比，樓層越高導致發生連續倒塌的概率越高。

表7 拆除不同樓層剪力墻

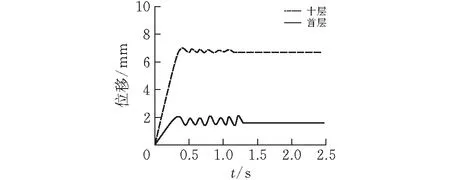
圖 8 不同樓層失效點位移

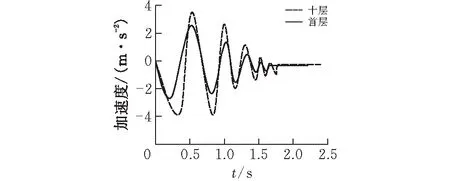
圖 9 不同樓層失效點加速度

4 結束語

通過建立一個24層典型框架-剪力墻結構模型，在SAP2000有限元軟件中利用非線性拆除構件法研究其抗連續倒塌能力。分別拆除首層和十層角柱、長邊中柱等典型柱構件以及剪力墻，分析這十種拆除工況的計算結果，得出了以下結論：

1)在角柱和短邊中柱位置布置剪力墻，在該柱失效后可明顯降低該柱節點的豎向位移從而增強其抗連續倒塌性能。

2)拆除不同樓層同一位置的柱子時，隨著構件所處層數的增高，失效點豎向位移以及塑性鉸轉角也相應變大。主要是因為底層結構相比于上部結構配筋率更大，使其極限承載能力高于上部結構，其上部結構超靜定次數相對上部構件失效較大，由此可知拆除底層柱后剩余結構仍有較大的冗余度。

3)在角柱和短邊中柱布置剪力墻，拆除長邊中柱后此結構發生連續倒塌的概率最大，中心柱次之，之后是角柱和短邊中柱。

4)在結構角部布置相互連接的L型剪力墻，即使L型剪力墻一個方向的墻體被拆除，結構的抗連續倒塌能力也不會降低多少，這是因為在一個方向的墻體被拆除后，在其垂直方向的墻體仍然可以較好完成內力重分布，使剩余結構具有很好的空間拉結作用，除次之外，失效后剩余墻體與其垂直方向墻體還會相互約束，也會增強抗連續倒塌能力。失效剪力墻構件所在層數的高度與結構動力反映的劇烈程度成正比，樓層越高導致發生連續倒塌的概率越高。