車內噪聲主動控制系統魯棒性分析與優化?

張立軍， 張希玉， 孟德建

（1.同濟大學汽車學院 上海，201804）（2.同濟大學智能型新能源汽車協同創新中心 上海，201804）

引言

主動噪聲控制的應用和研究中，系統魯棒性是非常關鍵的一個研究點。在車內噪聲主動控制中，由于汽車行駛工況復雜、使用特性多變，使得其對系統魯棒性的要求更加嚴苛。這也是主動噪聲控制系統在汽車應用發展緩慢的一個重要原因。

在主動噪聲控制領域，Bai等［1-2］運用魯棒控制理論，解決許多諸如管道、封閉聲場及頭戴耳機等噪聲主動控制的魯棒性問題。文獻［3-4］分別利用仿真方法，證明了魯棒控制相較于濾波最小均方誤差算法，在不穩定噪聲的控制中具有更好的效果。李普［5］將這一思想移植到聲振主動控制中，取得較好的效果。為了消除次級通路不確定性的影響，Thai等［6］提出了一種基于步長自適應和次級通路分解的無次級通路估計主動噪聲控制模型。王進軍等［7］提出了基于H∞魯棒性控制理論的有源控制器設計，有效克服了次級通路不確定性所引起的問題。Montazeri等［8］設計了一種自適應無限沖擊響應濾波器的主動聲振控制系統，使用改進的自適應算法使得系統有較好的穩定性。Zhang等［9-10］則應用在線建模方法，通過添加白噪聲激勵對次級通路進行實時辨識更新，但此法很難滿足實時性要求。Davari等［11］提出了一種基于新版本的濾波最小均方誤差算法的次級通路建模方法，通過仿真表明該方法對于次級通路模型的瞬變具有很強的魯棒性。Kim等［12］提出了一種用來估計次級通路定步長的歸一化最小均方誤差算法，仿真表明該方法提高了收斂速度，降低了穩態誤差。

上述文獻提出了多種提升次級通路魯棒性的方法，但均未涉及多通道自適應陷波系統魯棒性的研究。在車內噪聲主動控制系統中，由于乘員狀態、車窗開閉以及車輛行駛工況等汽車使用情況的多變性，導致系統中存在很大的不確定性。因此，急需對多通道自適應陷波的車內噪聲主動控制系統的魯棒性展開深入研究。

筆者首先建立了多通道自適應陷波的車內噪聲主動控制系統的離散狀態空間模型，定義了收斂率和穩態誤差增益來刻畫系統的降噪性能；其次，分析了導致系統不穩定的外在因素，并將其歸結為次級通路魯棒性問題，基于理論推導，對此魯棒性問題進行了深入的分析。還就次級通路魯棒性對系統收斂性的影響，以及次級通路完全失配的邊界條件進行了理論分析，并對分析結論開展了實驗驗證；最后，基于分析結果對次級通路估計進行優化設計，大幅提升系統的收斂性，并分析了次級通路反饋和泄露算法兩種方法來改善系統的魯棒性。

1 車內噪聲主動控制系統模型

圖1 為多通道自適應陷波車內噪聲主動控制系統框圖。考慮分析的普適性，假設系統包含M個麥克風和N個揚聲器，需要控制P個頻率成分的噪聲。

圖中d(n)為初級噪聲，假設其僅含P個待控制的諧波成分；y(n)為自適應陷波器輸出矢量；s(n)為麥克風輸入矢量；e(n)為系統誤差矢量；x(n)為參考信號矢量，其變形后得到參考信號矩陣X(n)；Hs為N×M維的次級通路傳遞函數矩陣；H?s為次級通路傳遞函數矩陣的估計；w(n)為自適應陷波器權系數矢量，是由最小均方誤差算法（least mean square，簡稱LMS）實時計算得到。

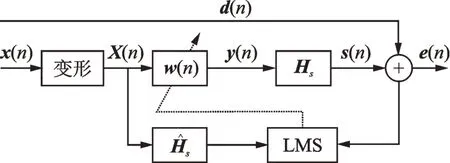
圖1 多通道自適應陷波算法Fig.1 Multi-channel adaptive notch filter algorithm

根據最速下降法可知權矢量的迭代公式為

其中：μ為收斂系數；R為濾波參考矩陣，可表示為

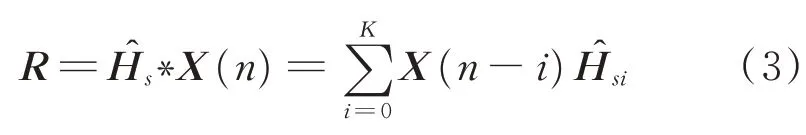
為了降低運算量，利用離散傅里葉變化對式（3）進行簡化，定義

則式（3）可以轉化為

1.1 次級通路魯棒性的離散狀態空間方程

根據最小化均方誤差原理，定義目標函數為

假設當J達到最小值時，w(n)≡wo，令

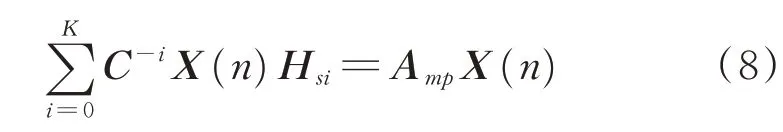
通過化簡可得

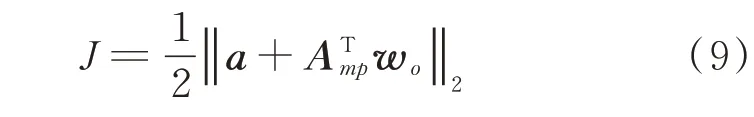
定義Δw(n)=w(n)-wo，則有

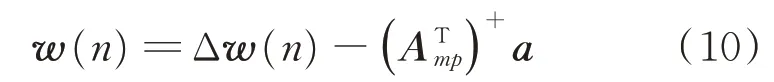
將式（1），（6），（7）帶入式（10），進一步簡化得到

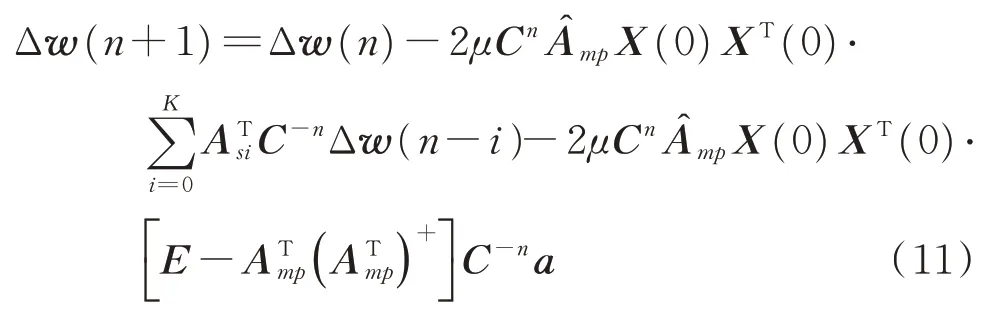
為了進一步簡化表達式，定義則收斂方程可以簡化為

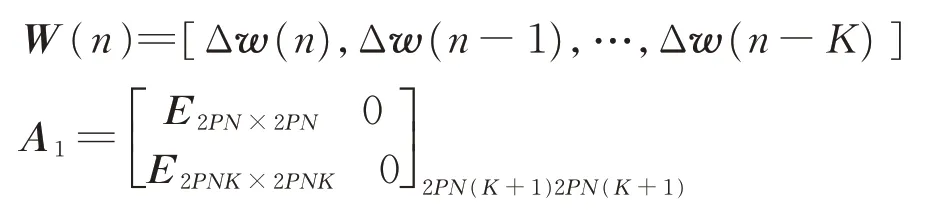
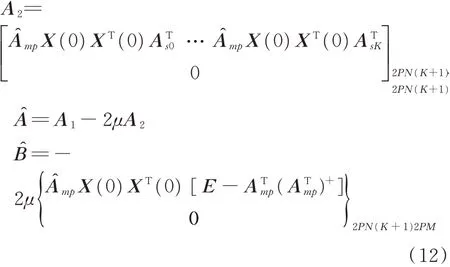
通過坐標變換把它變成一個時不變系統

為自適應陷波算法次級通路魯棒性問題等價離散系統狀態空間方程。

同理可以得到其輸出方程為

自適應陷波算法次級通路魯棒性等價離散系統狀態空間方程為

1.2 系統降噪性能評價指標

為了對系統的降噪性能進行量化評價，定義收斂率和穩態誤差。假設控制系統的目標函數J=0。此時，滿足條件a=-Ampwo，將其帶入式（14），結合式（8），（11），（12）將其化簡得到

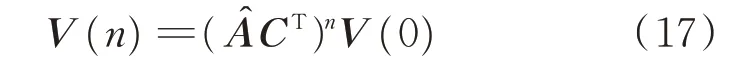
這里假設A?CT可以對角化，存在可逆矩陣D與對角陣使得A?CT=D-1ΛD。將其帶入式（17），并在等號兩邊取二范數得到并由二范數定義和范數相容原理可以推導得到

其中：ρ(?)為矩陣的譜半徑。

由式（18）可以看出，系統指數收斂。進一步推導得到收斂性與時間t和系統采樣頻率fs的關系為

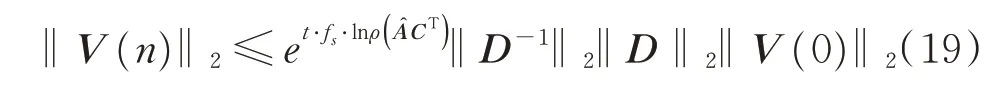
根據式（19），定義該系統的收斂率α為

當α＞0，系統收斂，且α越大，收斂時間越快。為了更加直觀反映系統收斂速度，定義時間常數τ

其物理意義是，收斂曲線在0點的切線與時間軸的切點如圖2所示。當過去τ時刻以后，系統可以收斂到37%；當過去3τ時刻，系統可以收斂到5%，一般此時認為系統已經完全收斂完畢，因此把3τ稱為系統的收斂時間。

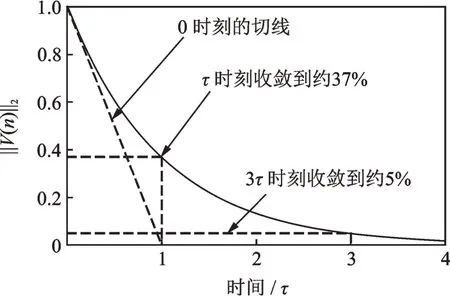
圖2 時間常數Fig.2 Time constant

假設系統收斂時，系統的狀態空間V（n）滿足

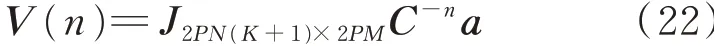
其中：J為一個待定矩陣。

將該假設帶入系統的狀態方程內，求取待定矩陣J，將其代入系統輸出方程式（15）中，獲得系統收斂時的穩態誤差為

定義

為自適應陷波器的穩態誤差增益。顯然，β越小，則系統對車內噪聲的抑制作用越好。化簡得到穩態誤差和穩態誤差增益為

由范數相容原理可以得到

不等號的存在，使得無法通過仿真的手段計算β的值，只有利用式（26）通過理論計算的方法，才能客觀評估系統穩態誤差的性能。

2 次級通路魯棒性分析

2.1 次級通路魯棒性

圖3 點劃線框內是系統控制器，點劃線框外是被控聲學系統和傳感通信部分。顯然，系統魯棒性問題主要是由點劃線框外的不確定性引起。本研究主要分析由次級通路不確定性引起的系統魯棒性問題。根據控制系統框圖可以看出，由次級通路引起的魯棒性問題主要包括：①次級通路估計誤差；②誤差信號傳感器的傳遞函數及其變化。

圖3 自適應濾波器示意圖Fig.3 Schematic diagram of adaptive filter

2.2 次級通路魯棒性影響因素

由式（25）可以看出，當系統完全收斂時，穩態誤差增益β中不包含次級通路估計項，也就不存在次級通路的估計誤差問題。由式（20）可以看出，系統的收斂率α中包含了次級通路的估計項。為了分析次級通路魯棒性對系統收斂性的影響，下文將用試驗和仿真相結合的方法來對其進行深入分析。

車內噪聲主動消聲試驗平臺以dSPACE實時仿真系統為核心，對外圍的軟硬件進行合理配置，如圖4所示。本研究硬件在環平臺包括MicroAutobox、揚聲器系統和麥克風模塊。使用的揚聲器為原車的4個車載揚聲器，麥克風使用了市售的OCROBOT麥克風模塊。

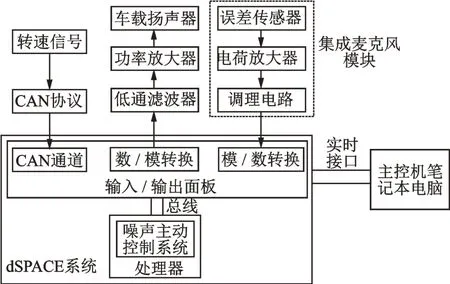
圖4 快速控制原型試驗平臺Fig.4 Rapid control prototype test platform

以發動機3 900 r/min的2階噪聲為控制目標的4揚聲器4麥克風配置系統為例，通過實車試驗標定標準工況（車內僅有駕駛員，且車窗全部關閉）、右后排一人工況、車窗全開工況、僅右前窗關閉工況的次級通路傳遞函數，并假設標定的傳遞函數為真實傳遞函數，即不考慮試驗誤差。然后，運用式（20）計算不同的次級通路導致的系統收斂率隨自適應算法收斂系數的變化情況，計算結果如圖5所示。

圖5 收斂率隨次級通路估計的變化Fig.5 Convergence rate changes with secondary path estimates

從圖5可以看出，當次級通路改變時，系統的收斂率、最優收斂率和最優收斂系數都發生了變化。其中，右后排一人工況的收斂率與最優收斂率都有所提升。說明次級通路的改變并不是一個壞事。但是，僅右前窗關閉工況中，無論收斂系數如何改變，系統都不會收斂。說明此時只改變系統的收斂系數，已經完全無法使系統產生降噪效果，這種情況稱之為次級通路完全失配現象。

為了進一步研究次級通路完全失配發生的條件，文中定義：若存在最大收斂系數μmax＞0，使得若收斂系數滿足0＜μ＜μmax，系統收斂率均有α＞0，則定義這種系統是可以收斂的；若找不到這樣的μmax，則定義這種系統完全不可能收斂，或稱這種系統存在次級通路完全失配現象。

2.3 次級通路完全失配的邊界條件

對于單通道系統，當次級通路與次級通路估計的相位差超過90°時，產生次級通路完全失配現象［13］。但是，這種方法不適用于多通道算法。一個N揚聲器M麥克風的自適應陷波器，共有N×M條次級通路。其中1～2條次級通路的相位差超過90°，并不一定會導致次級通路完全失配現象。為了得到多通道自適應陷波系統的次級通路完全失配的邊界條件，下面將借助理論推導方法對其進行分析。

假設系統沒有穩態誤差，則自適應陷波算法的收斂方程可以變為

當收斂系數μ非常小，則收斂過程非常緩慢，可以認為Δw(n-i)≈Δw(n)，用E[X(n)XT(n)]替代X(n)XT(n)，并對A?mp ATmp進行特征值分解

其中：Λ=diag(λ1，λ2，…，λ2PN)。

顯然，只有當

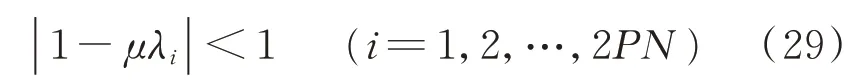
時，線性離散系統才是收斂的。由于μ非常小，可以進一步認為當Re(λi)＞0（i=1，2，…，2PN）時，系統是收斂的。

若有一個特征值向量指向復平面實值為1的豎線右邊，那么調整收斂系數，無法確保系統所有極點都落到單位圓內，導致次級通路完全失配現象的出現。

通過以上分析可以看出，在實際操作中，可以通過取一個極小的收斂系數μ，計算系統的收斂率。若在此極小的收斂系數下系統收斂率仍為0，那么一般情況下系統是不可能收斂的，即發生了系統次級通路完全失配的現象。

為了驗證文中分析結果的正確性，這里以上文標定的工況對結果進行校驗。計算僅右前窗關閉工況A?mp ATmp最大特征值隨頻率的變化。如圖6所示，曲線在130 Hz附近超過90°，所以從理論上系統在這個頻率上出現次級通路完全失配現象。而130 Hz對應發動機3 900 r/min時的2階噪聲頻率，這與計算的工況完全匹配。

同樣，對其他3個工況計算其特征值，結果如表1所示。從標準工況可以發現，如果不存在次級通路估計誤差，則系統特征值相角計算結果全部為0。對比標準工況與右后排坐一個人的工況發現，后者最大的相角不大，但是最大特征值與最小特征值的幅值比有所減小，這表示通過調整收斂系數μ可以讓其都更加接近0點，因此后一種工況可以到達更高的收斂速度。對比標準工況與車窗全部打開的工況發現，雖然后者特征值幅值比更加小，但是特征值普遍與x軸夾角較大，所以系統更加不容易收斂。綜上，如果不考慮系統的延遲，當

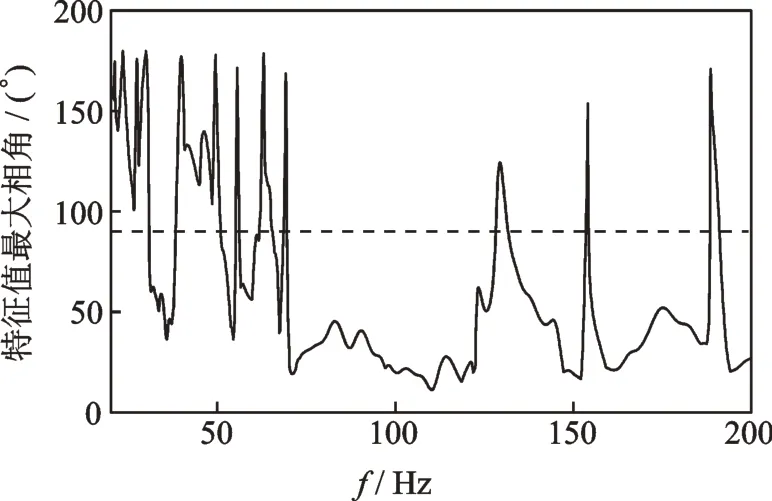
圖6 最大相角差隨頻率變化情況Fig.6 Maximum phase angle difference with frequency

表1 工況特征值統計Tab.1 Statistics of eigenvalues of different working conditions

3 次級通路魯棒性優化和改進

3.1 面向收斂速度的次級通路估計優化

為了提升系統的收斂速度，可以根據上文分析結果式（30）對次級通路進行設計優化。顯然，當設計

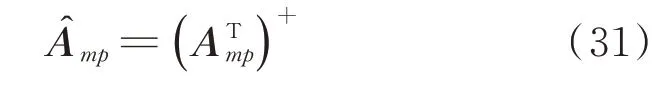
時，系統的收斂速度將發生大幅度提升。這里仍以控制130 Hz目標噪聲的4揚聲器4麥克風系統為例，分析結果如圖7所示。在次級通路估計優化前，系統最快的收斂率約為2.5，但是經過次級通路估計的優化，系統的收斂率超過了11.6。這從理論上說明這種優化方法可以提高多通道系統的收斂速度。

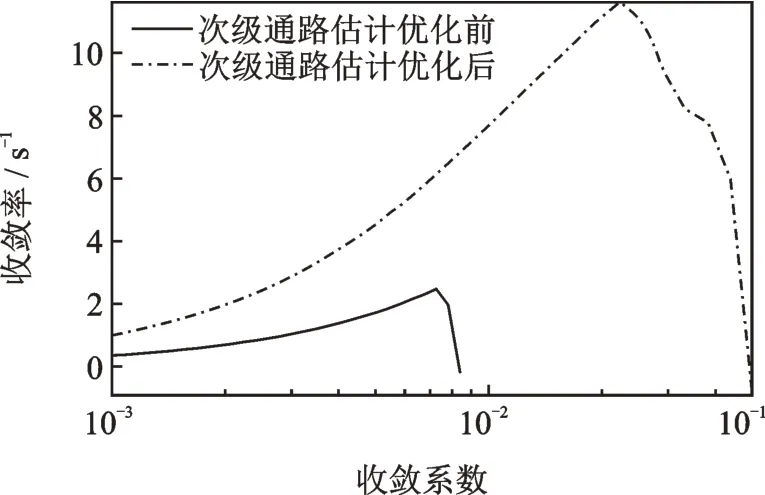
圖7 次級通路估計優化效果Fig.7 Effect of secondary path estimation optimization

為了進一步驗證上面的優化結果，以4揚聲器4麥克風系統怠速3 000 r/min靜止工況為例，通過實車試驗驗證改進次級通路對于系統降噪性能的影響，結果如圖8所示。實際收斂的曲線斜率與理論計算獲得的收斂曲線斜率基本相同，驗證了算法收斂速度估計方法的準確性；使用了改進的次級通路估計以后，系統的收斂速度大幅提升，驗證了上述優化結果的正確性。

圖8 次級通路估計對收斂速度的影響Fig.8 Impact of secondary path estimation on convergence speed

雖然這種優化方法可以大幅提升系統的收斂性，但不會提高系統的次級通路魯棒性。如圖9所示，使用優化的次級通路估計以后，系統仍然會發生次級通路完全失配現象，發生完全失配現象的頻率并沒有因為改進算法以后而減少。

3.2 次級通路魯棒性抑制——次級通路反饋

圖9 次級通路估計對系統魯棒性的影響Fig.9 Effects of secondary path estimation on the system robustness

為了解決自適應濾波算法的次級通路魯棒性問題，趙劍等［14］提出在次級通路回路上增加一個固定系數反饋控制器，以減小次級通道的不確定性［14］。在自適應陷波算法中，也可以采用相同的方法提升系統次級通路魯棒性。具體是在次級通路旁并聯一個反饋控制器，將誤差信號傳感器采集到的信號反饋回到系統的輸出。此時，系統的誤差矢量e（n）和新的次級通路傳遞函數變為

對Hb求導，根據Woodbury求逆公式，化簡可得

由式（33）可知，如果能夠設置控制器K，使得越小，新系統抑制次級通路變化的能力越強。可以證明(1-Hs K)-1與(1-KHs)-1擁有相同的不等于1的特征值。同時，根據譜半徑ρ(A)≤‖A‖這一特性，可以得到

若希望dHb盡可能小，則需要設計控制器K使得ρ(1-Hs K)盡可能大。若不計初級噪聲d（n），誤差項可以寫成

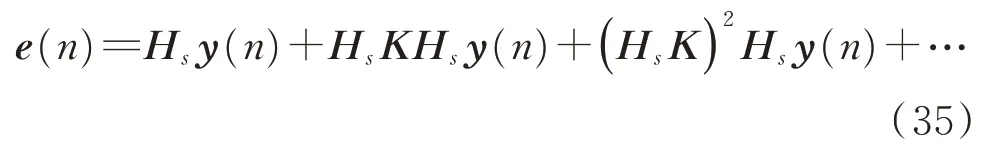
的等比數列，因此不難獲得，系統穩定的條件為等比系 數ρ(Hs K)＜1。實 際 設 計 時，可 以 先 給 定γ∈(0，1)，并設計控制器

即滿足設計要求。γ選擇越小，系統的次級通路魯棒性越差；γ選擇越大，則反饋系統內部的穩定性越差，系統越是容易發散。式（36）獲得的K是一個M×N階的復數矩陣，每個元素kij對應一個在某一頻率上滿足一定幅值相位特性的濾波器。選擇將元素kij轉換為一個二階濾波器，即

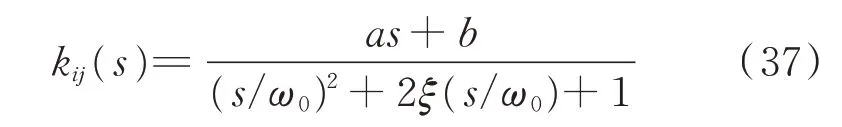
其中：傳遞函數的分母為一個二階震蕩環節；ω0為自適應陷波系統需要控制的角頻率；ξ為震蕩系統的阻尼比，阻尼比取很小；傳遞函數的分子是一個一階微分環節，用來使得整個濾波器的傳遞函數等于kij。

傳遞函數功能是將所控制的頻率過濾出來，避免初級噪聲d中ω0以外頻率成分的噪聲的傳遞函數滿足ρ(Hs K)＞1，使得反饋系統發生不穩定。

同樣用上節所分析的4個揚聲器4個麥克風系統為例進行分析。如果不使用次級通路反饋，系統必然發散。根據系統130 Hz的次級通路傳遞函數設計反饋控制器K，令γ=0.8，ξ=0.01。對新的系統進行仿真，仿真結果如圖10所示。圖中麥克風1～4分別對應車內左前、右前、左后和右后4個位置，實線為降噪前的聲壓，虛線為降噪后的聲壓。

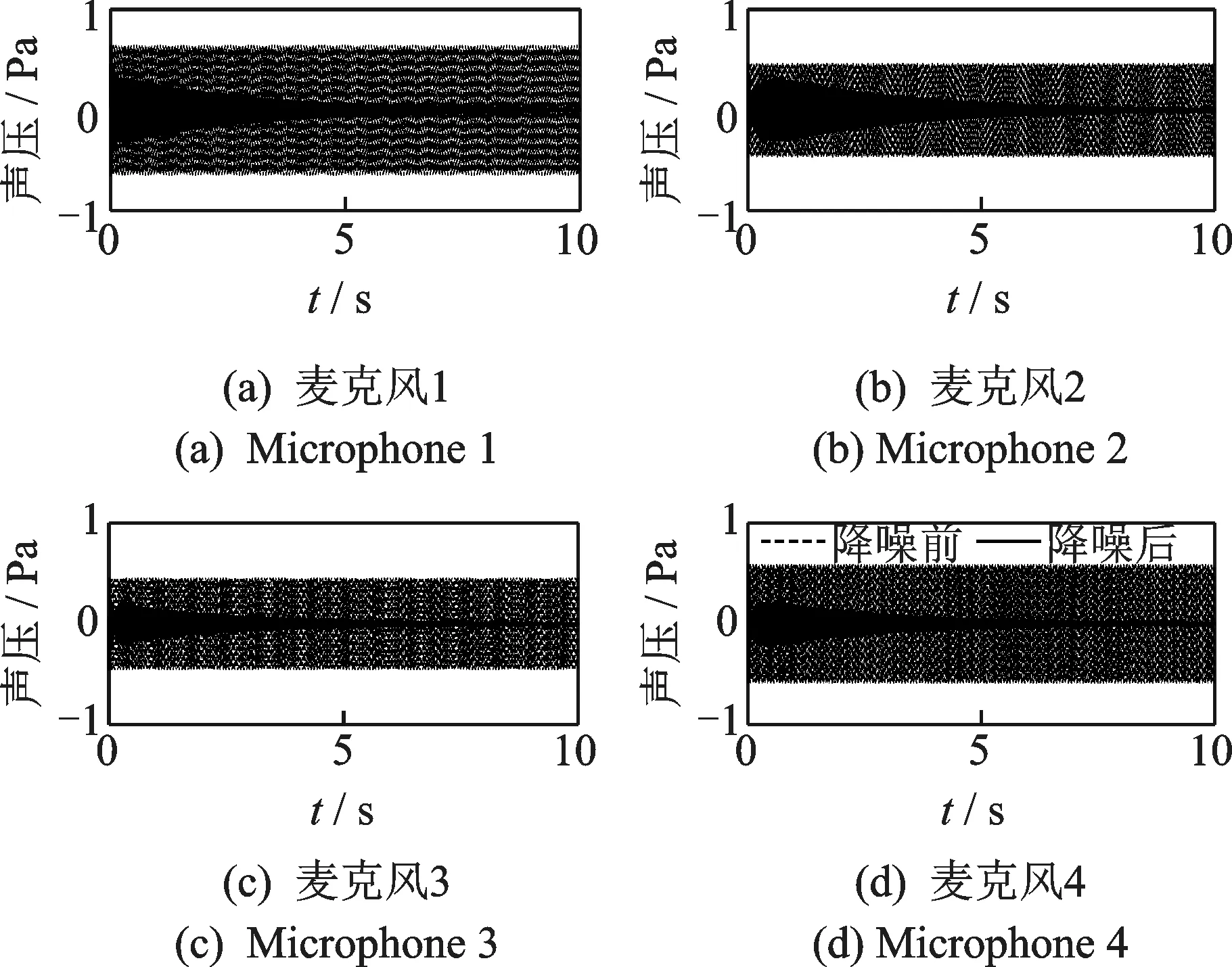
圖10 次級通路反饋的控制效果Fig.10 Control results of secondary path feedback

結果表明，次級通路反饋方法在提升系統次級通路魯棒性的同時，仍然可以保障穩態誤差為0，這使其擁有更好的降噪效果。除此以外，從式（32）可見，如果關閉自適應陷波器，那么系統的輸出為

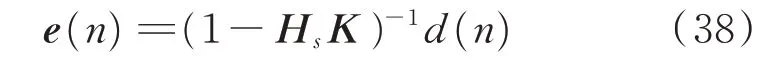
由于設計‖(1-Hs K)-1‖很小，所以系統對初級噪聲d仍然有削減的作用，此時這個反饋控制器成為了一個非自適應反饋控制的主動噪聲控制器。系統不打開自適應陷波器時的降噪性能如圖11所示。可以看出，這個反饋控制器也具有很好的降噪效果。降噪效果的好壞同γ的取值有關，γ越大，則系統的降噪效果越好。

圖11 關閉自適應陷波器后的控制效果Fig.11 Control results after closing the adaptive notch filter

由此可見，次級通路反饋的方式相比泄露算法，具有穩態誤差為0、具有非自適應降噪能力等優點，但是當次級通路的變化dHs過大，系統仍然可能發生次級通路完全失配現象。圖12所示，隨著γ的變大，特征值最大相角絕大部分情況下下降了，這說明次級通路反饋的確提高了系統的次級通路魯棒性。但是，仍然有一部分相角在90°以上，也就是說系統仍然存在次級通路完全失配的風險。

圖12 次級通路反饋對特征值最大相角的影響Fig.12 Effects of secondary path feedback on the maximum phase angle of eigenvalues

綜上，次級通路反饋方法不能徹底解決次級通路完全失配現象，尤其是對于車內噪聲這種次級通路變化范圍大、頻率范圍寬的系統。

3.3 次級通路魯棒性抑制——泄露算法

為了保證次級通路的魯棒性，自適應陷波算法的控制目標中還需要約束次級信號的大小，即

其中：β1為泄漏量。

根據最陡下降法原理得到泄露自適應算法的權矢量迭代公式為

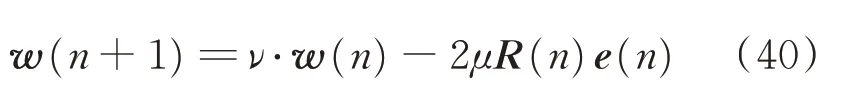
其中：ν=1-2μβ1為泄露因子，其取值越大，系統的次級通路魯棒性越好，但是系統的穩態誤差越大。

以4揚聲器4麥克風為例進行分析，次級通路估計的是駕駛員僅1人、車窗全部關閉的情況，但是真實的情況是只有右后排的車窗是關閉的。系統消除發動機3 900 r/min對應的2階噪聲。圖13是使用一般算法時系統的降噪效果，取收斂系數μ=10-2，可以明顯發現系統處于發散狀態。

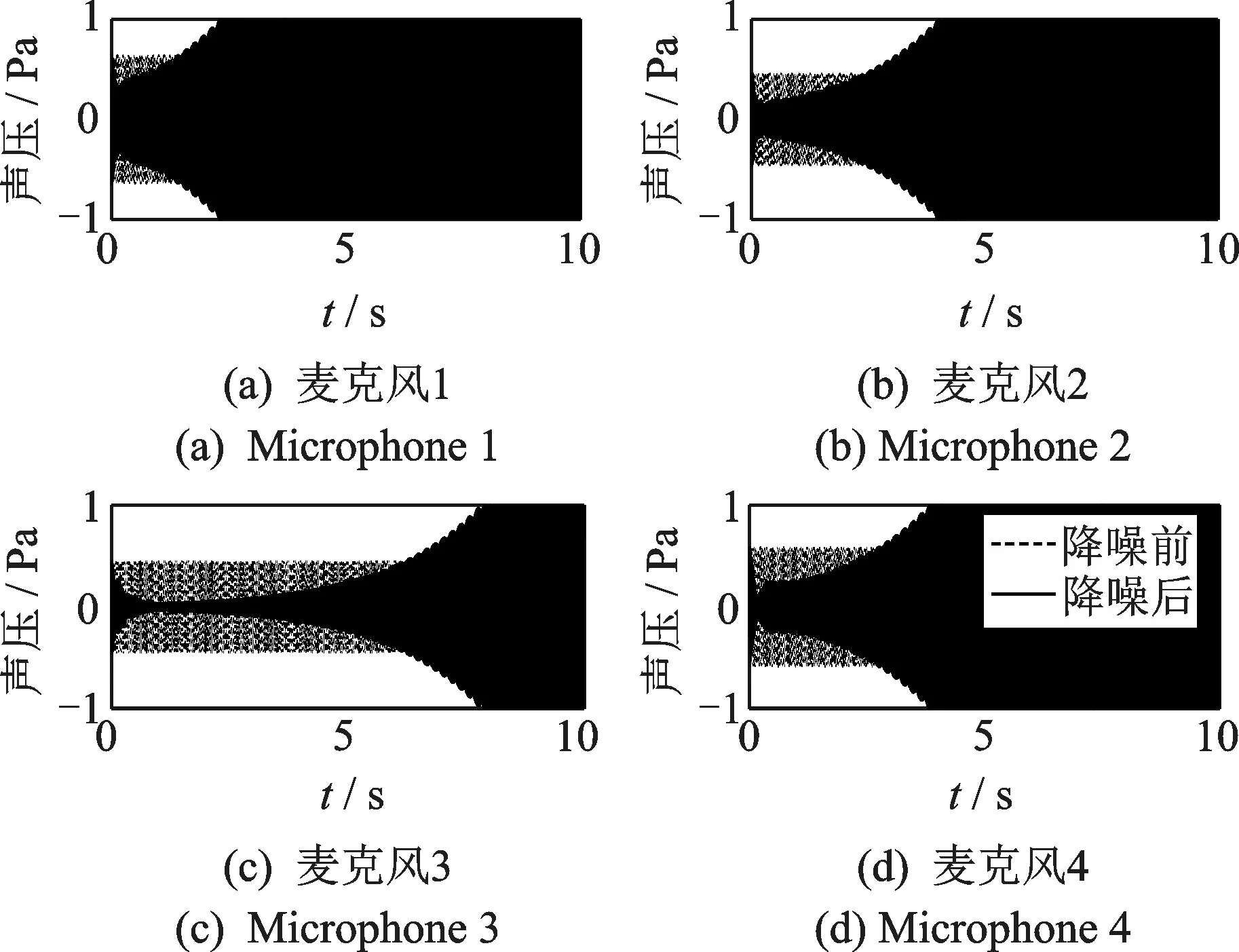
圖13 一般算法的降噪效果Fig.13 Noise reduction of the general algorithm

但是如果加入泄漏量β1=0.1，由圖14可以看出，系統可收斂，但有一定穩態誤差。

圖14 泄露算法的降噪效果Fig.14 Noise reduction of the leak algorithm

泄露算法在穩態誤差和穩定性之間存在矛盾，所以希望在系統穩定的前提下，讓泄漏量越小越好。

為了分析系統次級通路魯棒性，統計了以車窗全關為估計工況，所有開關窗情況下A?mp ATmp特征值最大相角的變化情況，工況代號分別表示左前、右前、左后與右后車窗的開閉情況，1代表開窗，0代表關窗。統計結果如圖15所示。

圖15 次級通路魯棒性統計結果Fig.15 Statistics of secondary path robustness

統計發現，次級通路完全失配現象并不是在任何頻率下都有出現的風險，容易出現次級通路完全失配現象的區域包括70 Hz以下、130 Hz附近、150～155 Hz附近、190 Hz附近。在這些區域可以適量設置泄漏量，而在其他次級通路完全失配風險較低的地方，可以設計泄漏量β1=0，以減小穩態誤差，提高系統的降噪性能。

以4揚聲器4麥克風系統為例，試驗驗證算法的可行性。工況為1 000 r/min靜置，由圖16可見，該工況下系統的次級通路魯棒性非常惡劣。由圖16（a）可見，此時如果不使用泄露算法，系統必然發散。如果引入一個β1=0.1的泄露算法，則系統能夠非常輕易地收斂。由此驗證了泄露算法對于提升次級通路魯棒性的重要作用。

圖16 泄露算法試驗驗證Fig.16 Leakage algorithm test verification

4 結束語

建立了多通道自適應陷波車內噪聲主動控制系統的離散狀態空間模型，提出評價系統降噪性能的收斂率和穩態誤差增益兩個指標。通過理論推導、數值仿真和實車試驗的方法，分析了系統的次級通路魯棒性問題，并推導了級通路完全失配的條件。分析表明，次級通路的改變對整個系統的穩態誤差沒有影響；對系統收斂性的影響有正有負，通過次級通路設計可以提升系統的收斂速度。結合分析結果對系統次級通路進行設計，通過改進次級通路，大幅提升系統的收斂速度。分析發現，次級通路反饋方法雖然可以提升系統魯棒性，但是存在次級通路完全失配的風險。泄露算法雖然是以犧牲系統問題誤差為代價來提升其魯棒性，但是可以杜絕次級通路完全失配的分析。在實際應用中更具前景。