風力機主軸承故障監測方法?

鄭玉巧，魏劍峰，朱 凱，董 博

（蘭州理工大學機電工程學院 蘭州，730050）

引言

風力機主軸承作為風力機傳動系統的核心部件，承受輪轂、葉片等部件帶來的多種變載沖擊作用，極易發生故障［1-2］。由于風力機主軸承在距離地面幾十米甚至上百米高的機艙內，一旦發生故障維護難度大、成本高，若未及時發現并解決故障會給風力機運行帶來嚴重影響甚至造成安全事故。因此，實現風力機主軸承的故障監測，及時發現故障征兆并開展維護，對于風力機健康運行、降低運維成本具有重要意義。

傳統風力機部件故障監測方法有振動分析［3-5］、聲發射監測［6-7］和電氣信號監測［8-9］等。其中振動監測法和聲發射監測法需要安裝大量的傳感器來采集信號，成本昂貴；此外安裝的傳感器一旦發生故障，不僅導致采集的數據可靠性降低，還增加額外的運維成本。相比風力機部件的振動信號和聲信號，電氣信號的采集不需要額外安裝傳感器［10］，但電氣信號中所包含的故障信息往往比較微弱，信噪比低，監測結果誤差較大。因此，上述方法難以在風力機部件實際監測中大范圍推廣。

目前，多數風電場通過安裝數據采集與監控系統（supervisory control and data acquisition，簡 稱SCADA）采集儲存風力機各部件運行參數及環境參數，因此選擇SCADA系統所記錄的風力機主軸承運行參數開展其故障監測研究。主軸承故障表現形式為磨損、點蝕或塑性變形等，故障早期主軸承滾過表面損傷點產生的異常摩擦又加劇故障程度，引起主軸承溫度特征的異常波動。鑒于此，本研究以SCADA系統所采集的風力機主軸承運行參數為研究對象，分別采用多元線性回歸（multiple linear regression，簡稱MLR）、灰色模型（grey model，簡稱GM）及支持向量機回歸（support vector machine regression，簡稱SVR）建立主軸承溫度單一預測模型及它們的組合預測模型，引入滑動窗口方法實時監測溫度預測殘差的均值和標準差變化情況，通過溫度預測殘差均值（或標準差）的置信區間與設定臨界值的對比來判斷主軸承運行狀態，從而實現對風力機主軸承的故障監測。

1 主軸承溫度組合預測模型的構建

1.1 問題描述與數據預處理

風力機SCADA系統通常以10 min為采樣周期記錄并傳輸風速、輸出功率及主軸承溫度等運行參數［11］，由于風力機SCADA系統輸出的各項運行參數單位不同，若直接用于建模分析對預測結果造成較大誤差，因此需要對原始數據進行歸一化處理，消除數據間的量綱影響。公式如下

其中：xmax為監測數據中的最大值；xmin為監測數據中的最小值；xi為原始監測值；x*為歸一化處理后的數據，x*的取值范圍為［0，1］。

1.2 多元線性回歸（MLR）模型

MLR模型闡述一個因變量依賴多個自變量的變化規律［12］。風力機主軸承溫度的變化視為多個變量參數影響下的共同作用結果，因此可將主軸承溫度作為因變量（即建模輸出變量），影響主軸承溫度變化的運行參數作為自變量（即建模輸入變量），建立主軸承溫度的多元線性回歸預測模型步驟如下。

設因變量（即風力機主軸承溫度）為y，m個自變量（即影響主軸承溫度變化的變量）分別為x1，x2，…，xm的多元線性回歸方程可表示為

其中：θ0為回歸常數；θ1，θ2，…，θm為回歸系數。

假設在實際問題中已測得n組監測數據（yi；xi1，，xi2，…，xim）（i=1，2，…，n），則式（2）可表示為

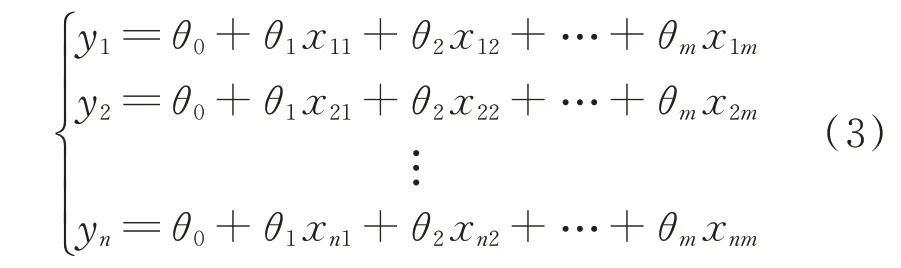
采用最小二乘法［12］可求解得到式（3）的回歸參數，將所求回歸參數代入式（2）后，需要對回歸方程進行統計量檢驗（F檢驗、T檢驗及多重共線性檢驗），若不滿足檢驗要求則需要重新尋找影響主軸承溫度變化的變量以便重新建模，滿足要求則可直接輸出模型。建模流程如圖1所示。

1.3 灰色預測模型GM（1，N）

灰色模型（GM）［13］具有建模數據少、預測效果好等優點。傳統的GM（1，1）模型是針對單一變量的預測，然而影響風力機主軸承溫度的因素是多變量共同作用的結果，因此GM（1，N）模型更適合建立風力機主軸承溫度預測模型。

由此可建立GM（1，N）模型為

其中：a為系統發展系數，反映預測值的發展趨勢；bj為驅動系數，反映原始數據的內在變化。

設置參數列μ=（a，b2，b3，…，bm）T，根據最小二乘法可求解式（6）得到參數列μ的值。

對GM（1，N）模型（式6）進行白化可得

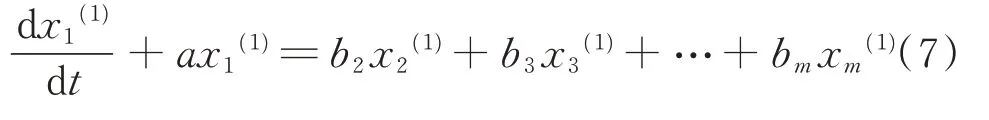
求解式（7）得到時間響應函數，表示為

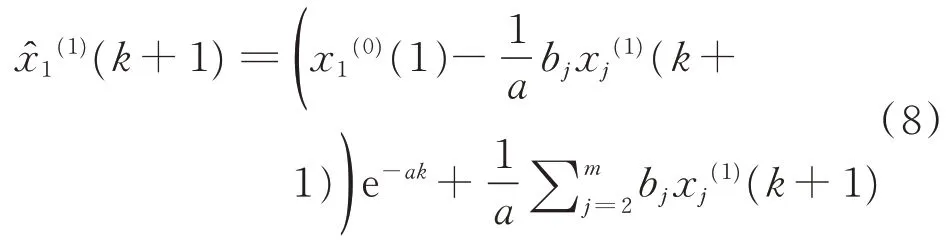
最終可得累減還原式（即灰色預測值）為

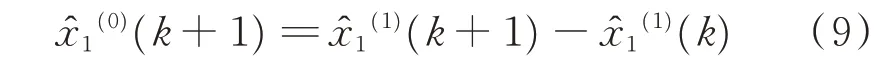
1.4 支持向量機回歸（SVR）模型

支持向量機回歸的核心思想是建立一個最優分類面，使得所有訓練樣本離最優分類面的誤差最小［14］。風力機主軸承溫度的SVR模型的訓練與預測借助LIBSVM工具箱實現。首先，選定一組風力機主軸承SCADA數據作為原始數據，對其進行歸一化處理；然后，根據工具箱提供的交互檢驗（cross validation，簡稱VC）功能尋求最優懲罰參數c和核函數參數g（由函數SVMcgForRegress實現）；最后，根據得到的最優參數c，g對SVR模型進行預測。

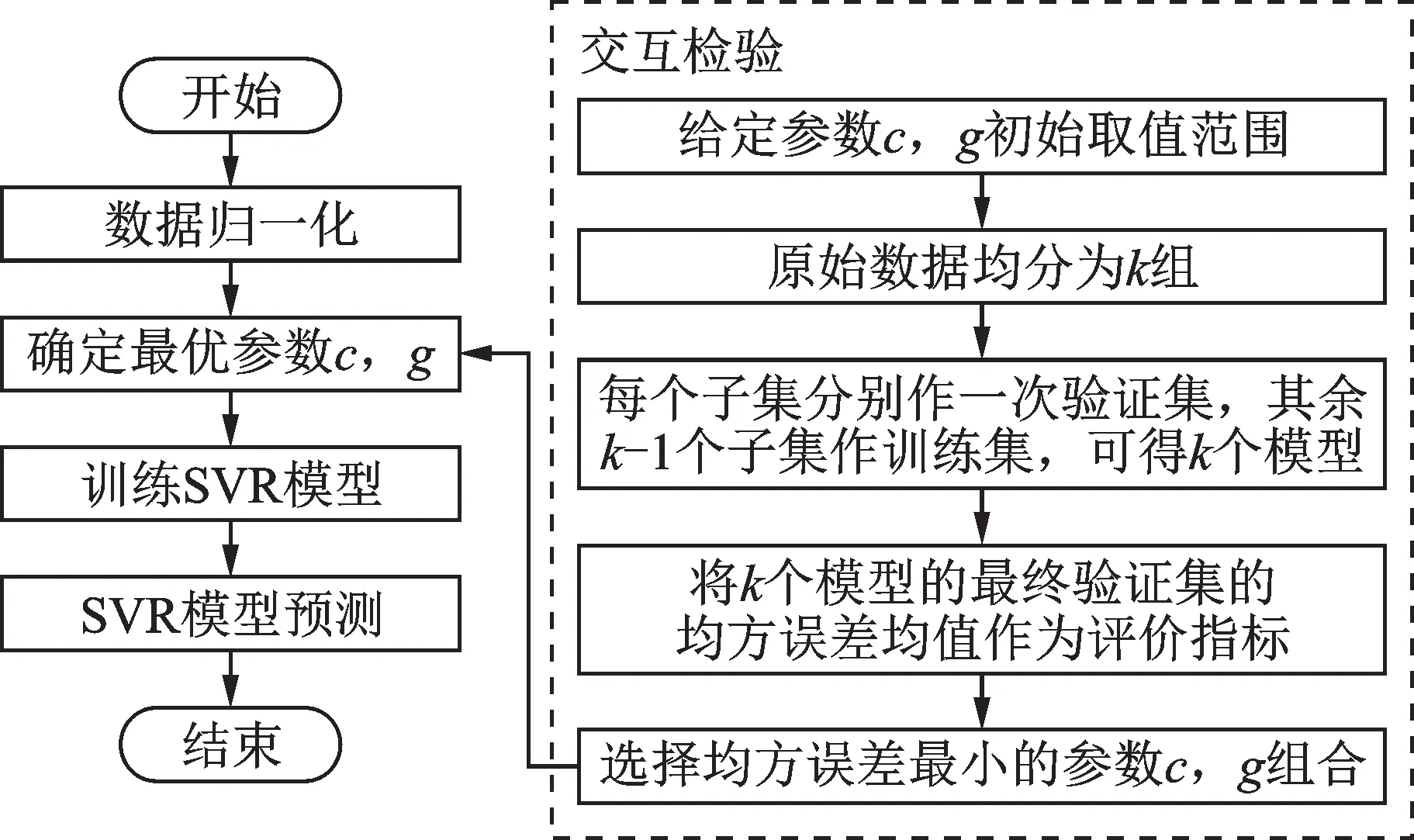
圖2 SVR算法流程圖Fig.2 Flow chart of SVR algorithm

1.5 組合預測模型

假設某預測問題共有f種單一預測模型，令yt表示t時刻的實際監測值，y?it表示第i種預測模型在t時刻的預測值（其中：i=1，2，…，f；t=1，2，…，n），第i種預測模型在t時刻的相對誤差為eit

由于每種單一預測模型具有其不足之處，而組合預測模型將不同類型的單一模型按照一定的權重比例重新組合可發揮各種單一模型優勢，有效削弱各種單一模型的不足以達到提高預測精度的目的。因此，建立基于熵值法［15］的組合模型，步驟如下：

1）求解第i種單一預測模型在t時刻的相對誤差比重pit

2）求解第i種單一預測模型與實際值的相對誤差熵值gi

3）求解相對誤差的變異系數di

4）求解各種單一預測模型的權重wi

5）求解組合預測模型值

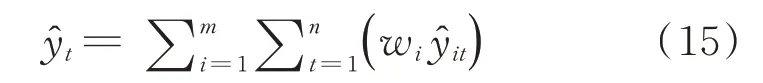
1.6 各模型綜合評價指標

為實現對各個預測模型的定量評價，選取均方根誤差（root mean square error，簡稱RMSE）、平均絕對百分誤差（mean absolute percentage error，簡稱MAPE）、平均絕對誤差（mean absolute error，簡稱MAE）及決定系數（R2）作為評價指標，求解公式如下

其 中：yt為 實 際 值為 預 測 值；RMSE，MAPE及MAE用來檢驗實際值與預測值的偏差及波動性大小，數值越小則表明預測模型精度越高；R2為自變量所解釋的變化量占總變化量的比例，R2取值為［0，1］，R2越接近于1則表明預測精度越高。

2 殘差統計特性分析及故障監測

2.1 滑動窗口殘差統計特性分析

假設風力機主軸承溫度在t時刻的實際監測值為yt，預測模型在t時刻的預測值為則預測殘差序 列 為預 測 殘 差序列的統計特性可由殘差均值及殘差標準差反映。為準確描述預測殘差的統計特性（均值和標準差）變化情況，采用滑動窗口方法［16］求解預測殘差序列的窗口均值及窗口標準差，滑動窗口如圖3所示。

圖3 滑動窗口示意圖Fig.3 Schematic diagram of sliding window

設定寬度為N的滑動窗口，則窗口內的N個殘差的窗口均值μ和窗口標準差σ求解公式為

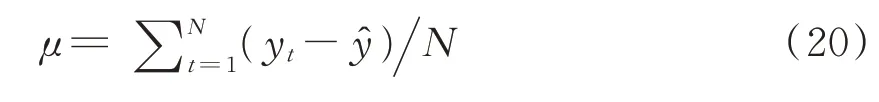
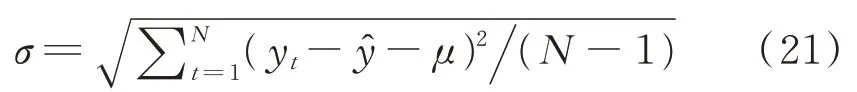
2.2 主軸承的故障監測

主軸承正常工作時，溫度預測值與實際溫度值接近，其殘差序列分布穩定；然而主軸承發生故障會引起其溫度的異常波動，進而帶來預測殘差統計特性的異常變化。具體表現為以下3種情況：①主軸承溫度預測殘差的窗口均值μ未發生較大改變，但其窗口標準差σ變化顯著，殘差范圍增大；②主軸承溫度預測殘差的窗口標準差σ未發生較大改變，但其窗口均值μ變化顯著，出現系統偏差；③主軸承溫度預測殘差的窗口均值μ及標準差σ均變化顯著。

基于上述情況，可根據預測殘差序列的統計特性變化來監測主軸承運行狀態，設定殘差均值和殘差標準差故障臨界值分別為μv和σv。當溫度預測殘差的均值或標準差超過某一臨界值時，系統產生故障報警告知維護人員進行檢修。假設滑動窗口的溫度殘差序列均值絕對值最大值為μmax，標準差絕對值最大值為σmax，則主軸承溫度故障的臨界標準為

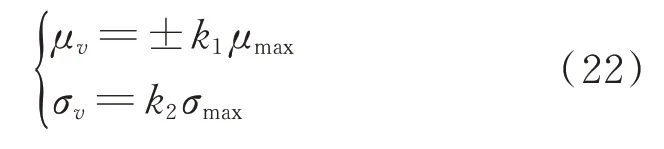
式（22）中k1，k2可由現場運維人員根據經驗確定。根據預測模型對主軸承溫度進行預測時，會存在各種不確定性因素對輸出結果造成干擾［17］。為簡化起見，將預測殘差序列假設為一組均值和方差未知的正態分布數據，在求解殘差窗口均值和標準差時需要給出置信度為1-α的均值和標準差的置信區間，表示為

其中：tα/2為t分布的α/2分位點為χ2分布的α/2分位點，其值在給定置信度1-α后可通過查閱t分布臨界值表和χ2分布臨界值表得知。

當殘差均值或標準差的置信區間超過各自臨界值時，發出風力機主軸承故障報警信息。

3 案例分析

3.1 建模變量的選取

根據文獻［18］可知，關鍵部件溫度相關聯的特征量主要包括環境溫度、風速、轉速及功率等，此外由于部件溫度的熱慣性特點使得前一時刻的部件溫度對當前時刻部件溫度有直接影響。因此，建立主軸承溫度預測模型時初步選擇風力機輸出功率、風速、環境溫度、主軸轉速及上時刻主軸承溫度作為輸入變量，主軸承當前時刻溫度（y）作為輸出變量。

選取某風力機2019年4月主軸承正常狀態時的運行參數進行建模，根據所建模型對5月份主軸承溫度進行預測。按照1.1部分所述步驟對原始SCADA數據進行歸一化處理，歸一化后的部分數據如表2所示。

表1 SCADA數據的歸一化Tab.1 Normalization of SCADA data

3.2 MLR，GM（1，N），SVR及組合預測模型的求解

3.2.1 多元線性回歸模型(MLR)

以風力機輸出功率（x1）、風速（x2）、空氣溫度（x3）、主軸轉速（x4）及上時刻主軸承溫度（x5）為自變量，風力機主軸承當前時刻溫度（y）為因變量建立多元線性回歸方程，根據1.1部分所述步驟求解得到的MLR模型為

對式（25）進行統計量檢驗時發現輸出功率（x1）所對應的方差擴大因子（variance inflation factor，簡稱VIF）為15.641 8，風 速（x2）所 對 應 的VIF為15.713 4，表明所建模型存在嚴重的多重共線性（VIF＞10），可能會給回歸結果帶來較大誤差，因此需要重新修正模型輸入變量，以消除多重共線性。

消除多重共線性的常用方法則是剔除VIF最大值所對應的變量，即風速（x2）；剔除后的MLR修正模型自變量為風力機輸出功率（x1）、空氣溫度（x3）、主軸轉速（x4）及上時刻主軸承溫度（x5），根據1.1部分所述步驟求解得到的MLR修正模型為

據檢驗，式（26）已消除多重共線性，F檢驗及T檢驗各項指標均滿足顯著性條件。利用修正后的MLR模型對5月份主軸承溫度進行預測，部分預測值及殘差值見表2。

表2 MLR模型部分溫度預測結果值Tab.2 Temperature prediction results of MLR model℃

3.2.2 灰色預測模型GM(1,N)的求解

基于MLR修正模型所得自變量及因變量，選擇當前時刻主軸承溫度、功率、空氣溫度、主軸轉速及上時刻主軸承溫度的時間序列為原始數據序列其中：當前時刻主軸承溫度數據序列為系統特征數據序列；而功率數據序列空氣溫度數據序列主軸轉速數據序列以及上時刻主軸承溫度序列均為相關因素序列。選取2019年4月份SCADA數據依據1.2所述步驟進行建模，求解得到GM（1，N）模型參數列μ的值為

μ=(2.014 5，-0.000 6，0.062 5，0.146 5，1.972 3)T

將參數列μ代入式（8），得到時間相應函數，而后根據式（9）累減可得到GM（1，N）預測值，部分預測值及殘差見表3。

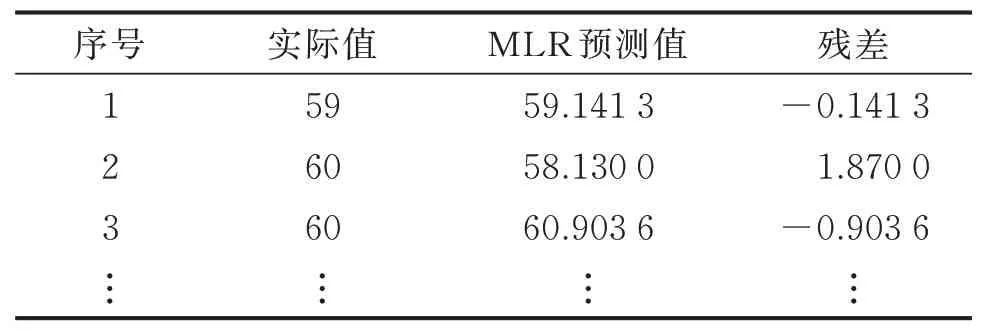
表3 GM(1,N)模型部分溫度預測結果值Tab.3 Temperature prediction results of GM(1,N)model ℃

3.2.3 支持向量機回歸模型(SVR)的求解

基于MLR修正模型所得自變量及因變量，選擇2019年4月份的當前時刻主軸承溫度、功率、空氣溫度、主軸轉速及上時刻主軸承溫度等序列數據用來訓練SVR模型，用訓練好的模型來預測5月份主軸承溫度值。

給定參數c和g的初始范圍均為［-8，8］，根據交互檢驗法求解得到SVR模型最優參數c和g為：Bestc=1.414 2，Bestg=0.353 5；根據所求最優參數c和g對SVR模型進行訓練，然后對5月份數據進行預測，部分預測值及殘差值見表4。

3.2.4 MLR、GM(1,N)及SVR組合模型的求解

假設MLR修正模型所得主軸承溫度預測值為y?1t，GM（1，N）模型所得預測值為y?2t，SVR模型所得預測值為則應用熵值法確定的各模型最優權重為w1=0.125 8，w2=0.310 5，w3=0.563 7，因此可得組合模型表達式為根據所求組合模型對5月份數據進行預測，部分預測值及殘差見表5。

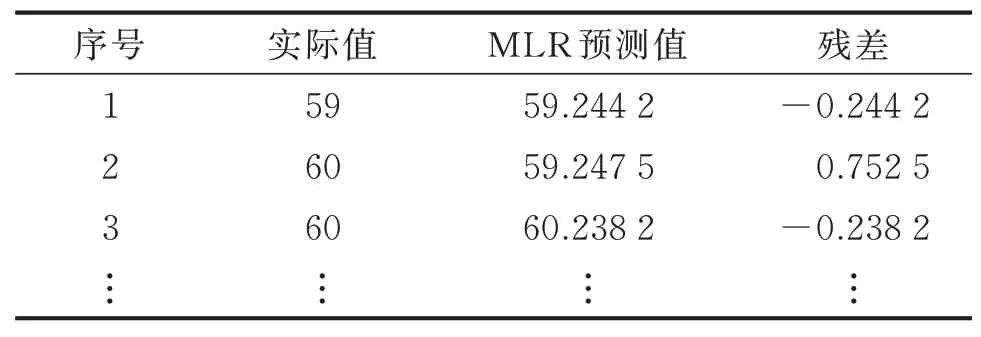
表4 SVR模型部分溫度預測結果值Tab.4 Temperature prediction results of SVR model℃

表5 組合模型部分溫度預測結果值Tab.5 Temperature prediction results of Combined model ℃

3.3 各模型預測結果對比分析

根據各模型對5月份主軸承溫度數據進行預測，實際值與各模型預測值變化趨勢如圖4所示。

圖4 風力機主軸承溫度預測圖Fig.4 Forecast figure of wind turbine main bearing temperature

圖4 顯示在第48，1 220，1 928及2 206點附近處主軸承溫度較低，查詢主狀態日志可知是由于風力機停機重新啟動所造成。另外從圖中可看到，不同模型所求主軸承溫度預測值與實際值變化趨勢相近，擬合程度較高；但根據圖4不易直觀判斷哪種模型預測值與實際值吻合度更好。為進一步對比各模型優劣性，進而求解各模型綜合評價指標值，見表6。

表6 各模型指標對比值Tab.6 Comparison results of each model index

由表5的各指標數據對比可知，組合模型的RMSE，MPE及MAE最小，R2最大，表明組合模型偏差及波動性更小，在各模型中具有最高的預測精度；其中組合模型的R2值分別較其他模型提高0.049 3，0.002 7和0.000 2。因此，選擇在組合預測模型基礎上引入滑動窗口方法實現對風力機主軸承的故障監測。此外在單一預測模型中，SVR模型具有良好的預測精度，各項指標均和組合模型指標相近。

3.4 基于滑動窗口的主軸承溫度故障狀態監測

查詢風力機主狀態日志可知，5月份風力機主軸承未發生故障。為驗證方法有效性，人為模擬主軸承因發生故障而導致主軸承溫度升高的情況。選擇5月份主軸承溫度較高的12～15號3天累計568個溫度點進行研究，取滑動窗口寬度N=20，置信水平α=0.05，根據式（23），（24）求解得到主軸承正常狀態下預測殘差均值及標準差的各自95%置信區間，它們的變化趨勢如圖5所示。

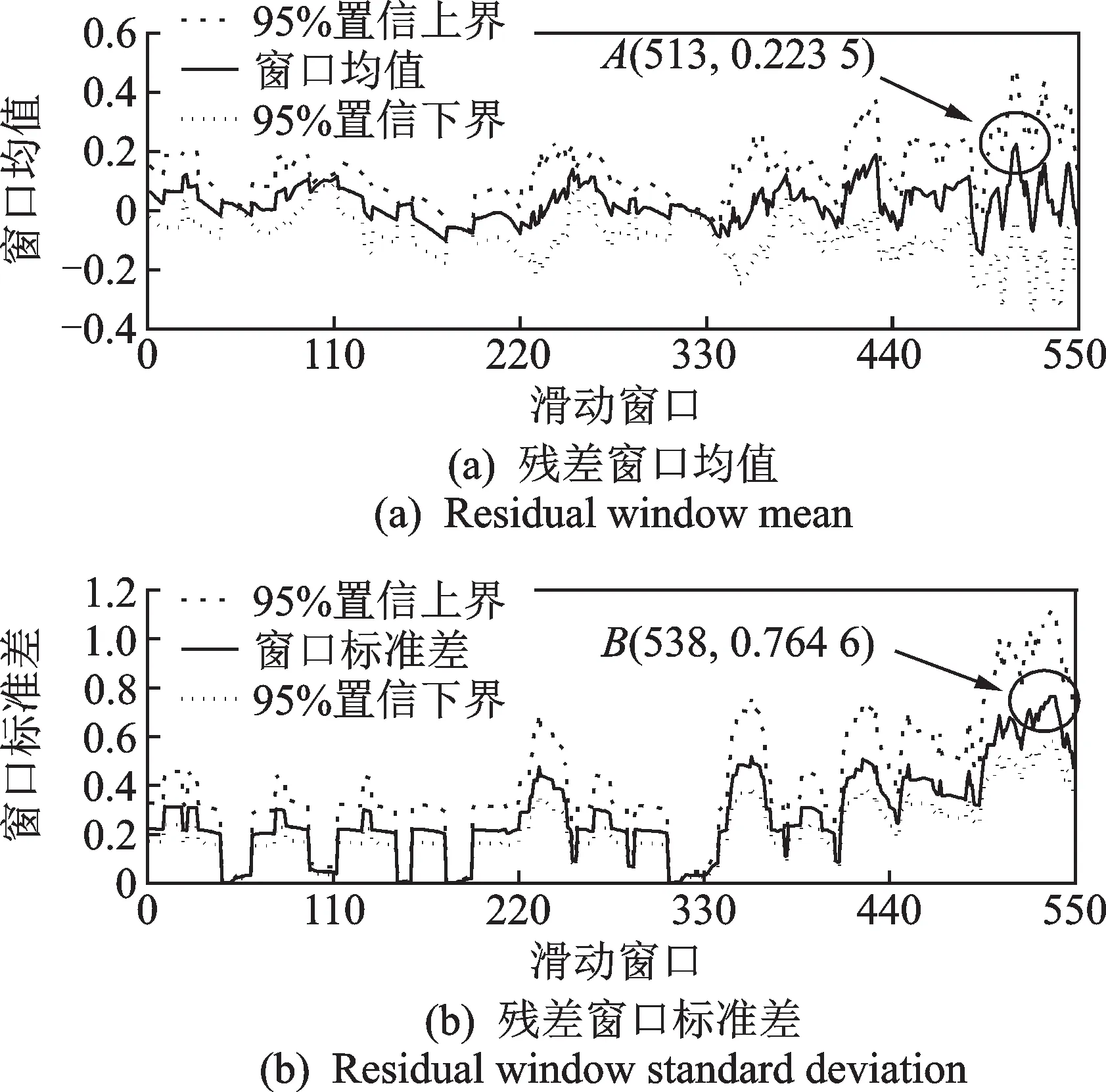
圖5 殘差窗口均值和標準差Fig.5 Residual window mean and standard deviation

圖5 （a）為主軸承溫度殘差窗口均值變化趨勢圖，從圖5（a）可知主軸承溫度殘差窗口均值最大值為μmax=0.223 5（即A點）；圖5（b）為主軸承溫度殘差窗口標準差變化趨勢圖，由圖5（b）可知主軸承溫度殘差窗口標準差最大值為σmax=0.764 6（即B點），由于是人為模擬故障，所以殘差標準差并未發生變化。故選擇殘差窗口均值展開分析，取k1=2，則窗口均值臨界值根據式（22）可得μv=±0.447 0。

從第303個溫度點開始人為加入步長為0.015℃的溫度累積偏移量，基于組合模型的主軸承溫度預測殘差均值變化趨勢如圖6所示。

圖6 模擬故障狀態的殘差窗口均值Fig.6 Residual window mean value of simulated fault state

圖6 顯示，主軸承正常運行時殘差均值95%置信區間均未超過臨界值，在C點即第284個窗口（303-20+1）加入溫度偏移后，滑動窗口殘差均值逐漸增大，在D點殘差窗口均值95%置信上界超過臨界值0.447 0，引發主軸承故障報警。綜上可得，當主軸承發生故障導致其溫度異常時，基于滑動窗口方法的故障監測方法可及時發現故障并報警，有效監控主軸承異常狀態。

4 結束語

基于風力機SCADA數據分別建立主軸承溫度的MLR，GM（1，N），SVR 3種單一預測模型及它們的組合預測模型；其中組合模型有著更優越的預測性能，其決定系數分別比其他模型提高0.049 3，0.002 7及0.000 2。此外SVR模型在單一預測模型中有著更高的預測精度。在組合預測模型基礎上引入滑動窗口方法求解分析溫度預測殘差的統計特性（均值和標準差），當窗口均值或標準差的置信區間超過設定臨界值時可判斷出主軸承發生故障，有效監測主軸承運行狀態。筆者所提方法可用于工程實際中風力機或其他機械設備的關鍵部件溫度預測及故障監測。