采用小生境遺傳算法反演淺海聲速剖面研究?
崔寶龍 徐國軍 笪良龍 過武宏
(1 海軍潛艇學院 青島 266199)
(2 青島海洋科學與技術國家實驗室海洋軍民融合聯合實驗室 青島 266237)
(3 國防科技大學氣象海洋學院 長沙 410073)
0 引言
海洋聲層析技術(Ocean acoustic tomography)是近幾十年來海洋研究領域的一個重要方向,而聲速剖面反演則是海洋聲層析技術的一個重要內容。聲層析剖面反演是以匹配思想為核心,利用觀測信號的某些特征作為觀測量,聲場傳播模型計算的特征作為拷貝量,進行反向運算進而推導出剖面參數的技術[1]。海洋聲層析最早由先Munk 和Wunsch等[2?3]提出,利用聲線的傳播時間反演深海環境下聲速剖面;之后國內外學者相繼提出許多聲速剖面的反演方法,例如基于聲波峰值到達匹配的方法[4]、基于簡正波傳播時間層析方法[5],匹配場層析[6]等。聲速剖面反演的本質是一個多維優化問題,為了獲得更好的反演結果,應盡可能將待反演參數減少,從而減少運算量并提高反演精度和穩定性。Davis等[7]研究表明,經驗正交函數(Empirical orthogonal function, EOF)可作為基函數描述淺海聲速剖面,從而有效降低反演參數維度。沈遠海等[8]利用實驗驗證了使用EOF 表征聲速剖面的可行性。
在聲速剖面反演模型中,聲場模型中反演參數與聲場之間均呈現非線性關系,從而使得算法無法獲得唯一解。為此需建立對應的代價函數,采用優化算法在給定參數空間范圍內尋找最優解。因此,選擇一種快速有效的搜索算法成為聲速剖面反演的重要一環。遺傳算法是常用的搜索優化算法并已經在大量領域成功應用,遺傳算法是將問題的解表示成“染色體”并置于問題的“環境”中,并按適者生存的原則,通過交叉、變異等一系列的過程,迭代進化直至收斂到最適應環境的一個染色體上,即問題的最優解。遺傳算法已在諸多領域廣泛應用,但是在對復雜問題進行優化時存在早熟收斂和全局搜索性差等問題。針對于此,采用小生境遺傳算法(Niche genetic algorithm, NGA)替代傳統遺傳算法,小生境算法的基本思路在個體進化過程中選擇特定生存環境,通過增加種群多樣性來改善早熟收斂等問題[9?10]。Rudolph[11]證明了傳統遺傳算法無法達到全局最優解,但如果保留每一代中最優個體則可使算法達到最優解。小生境算法一方面采用交叉算法降低子代個體不確定性,同時令μ個父代與λ個子代同時競爭以提高選擇壓,二者結合既避免早熟收斂又能獲得最快的局部搜索速度[12]。
基于上述分析,本文結合聲速剖面的EOF 分解,基于小生境遺傳算法研究聲速剖面的反演問題,給出具體反演流程,利用2019年海上實驗數據對淺海負躍層環境下的聲速剖面反演進行了數值驗證,并對比分析了遺傳算法與小生境遺傳算法反演剖面精度問題。
1 理論模型
1.1 聲速剖面的經驗正交函數表征
在實際淺海環境條件下,聲速剖面曲線復雜多變,簡單的聲速隨深度線性變換的模型無法表征,也就意味著需要較多的參數來表示。經驗正交函數是一組相互正交的、用來描述樣本相對于平均聲速結構變化的函數向量,通常情況下,僅需前幾階EOF就可以表征一定范圍內的剖面,達到降低聲速剖面參數維度的目的,可用其來描述樣本相對于平均結構的變化情況。相關理論在文獻[7–8]中已有詳盡闡述,本文不再贅述。對聲速剖面通過EOF方法進行計算,則聲速剖面可化為
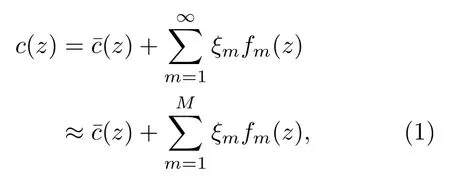
1.2 小生境遺傳算法
小生境遺傳是對遺傳算法的改進,基于排擠、基于清除或基于共享等函數的改進較為常見,本研究采用應用較為廣泛的基于排擠的小生境算法[13]。基于排擠的小生境遺傳算法的基本思想可總結為首先計算每兩個個體之間的相似度,本研究中使用海明距離-度量個體間相似度這一指標進行計算[14]。如果某兩個個體的海明距離在特定距離內,則適應度較低的個體給予處罰,使得其在進化的過程中被淘汰的概率更大。這樣也就保證了在特定距離內僅保留一個優良個體,從而在種群個數為定值的條件下保證了個體在空間內分散分布,相當于提高了種群的多樣性。基于排擠的小生境算法過程如下[15]:
(1)隨機生成種群數為M個的群體,計算每個個體適應度Fi;
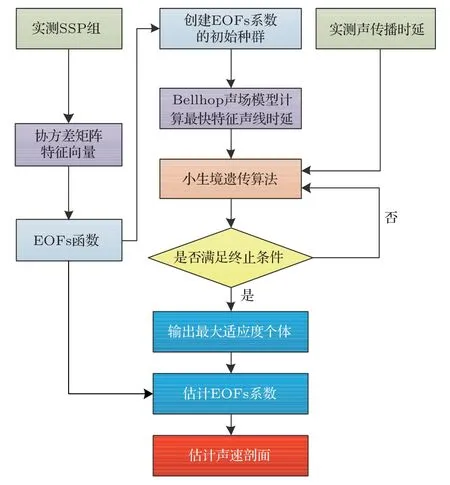
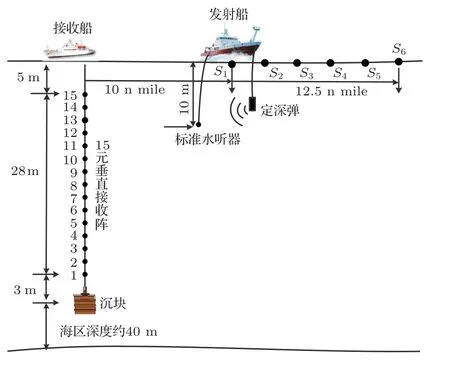
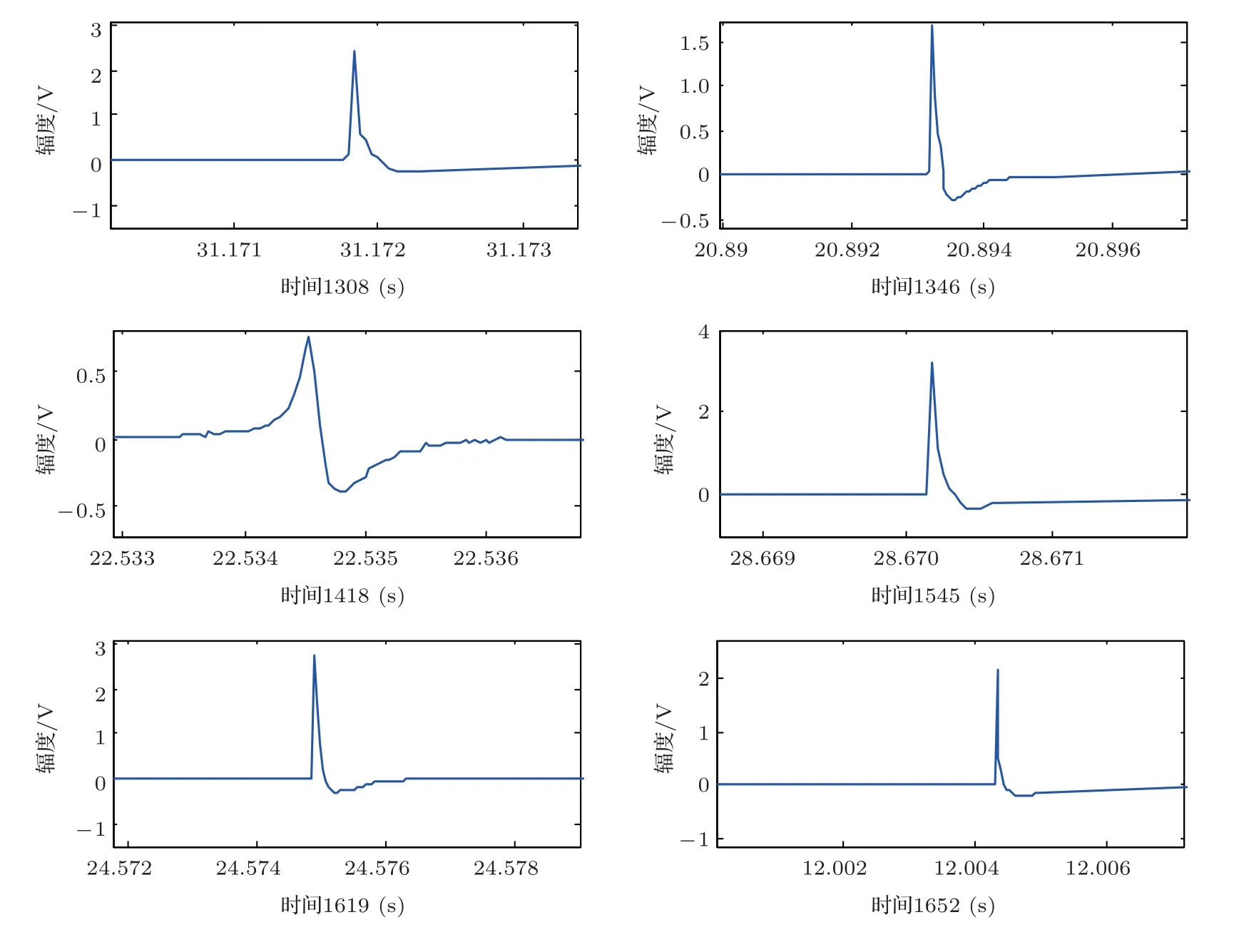
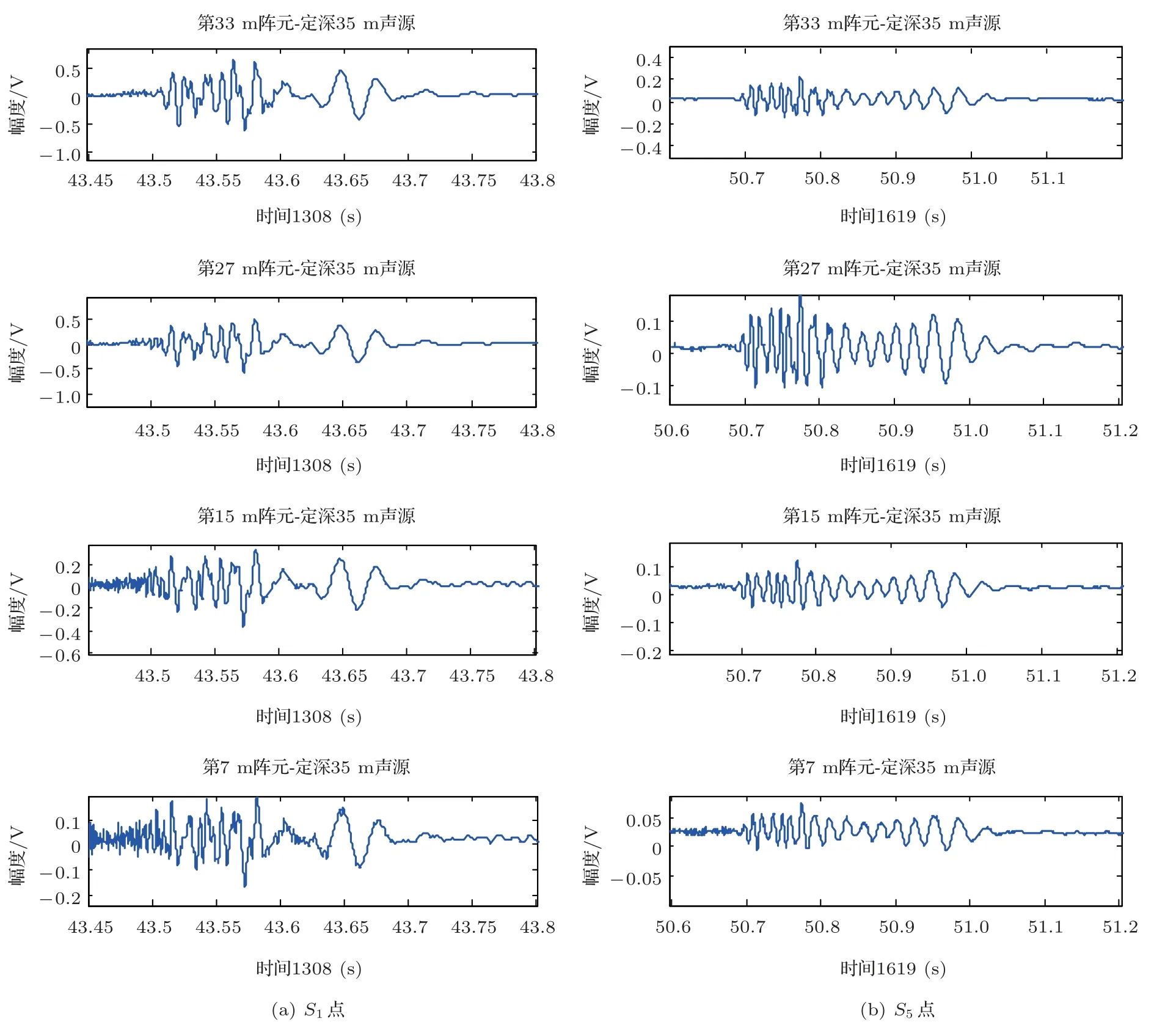
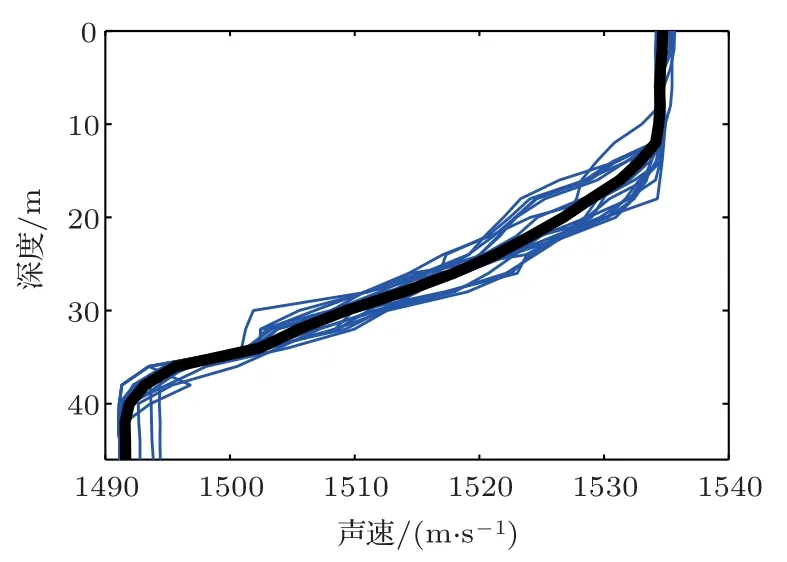
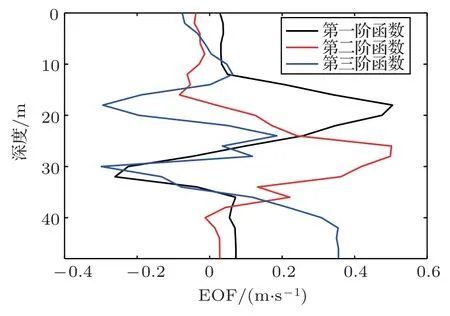
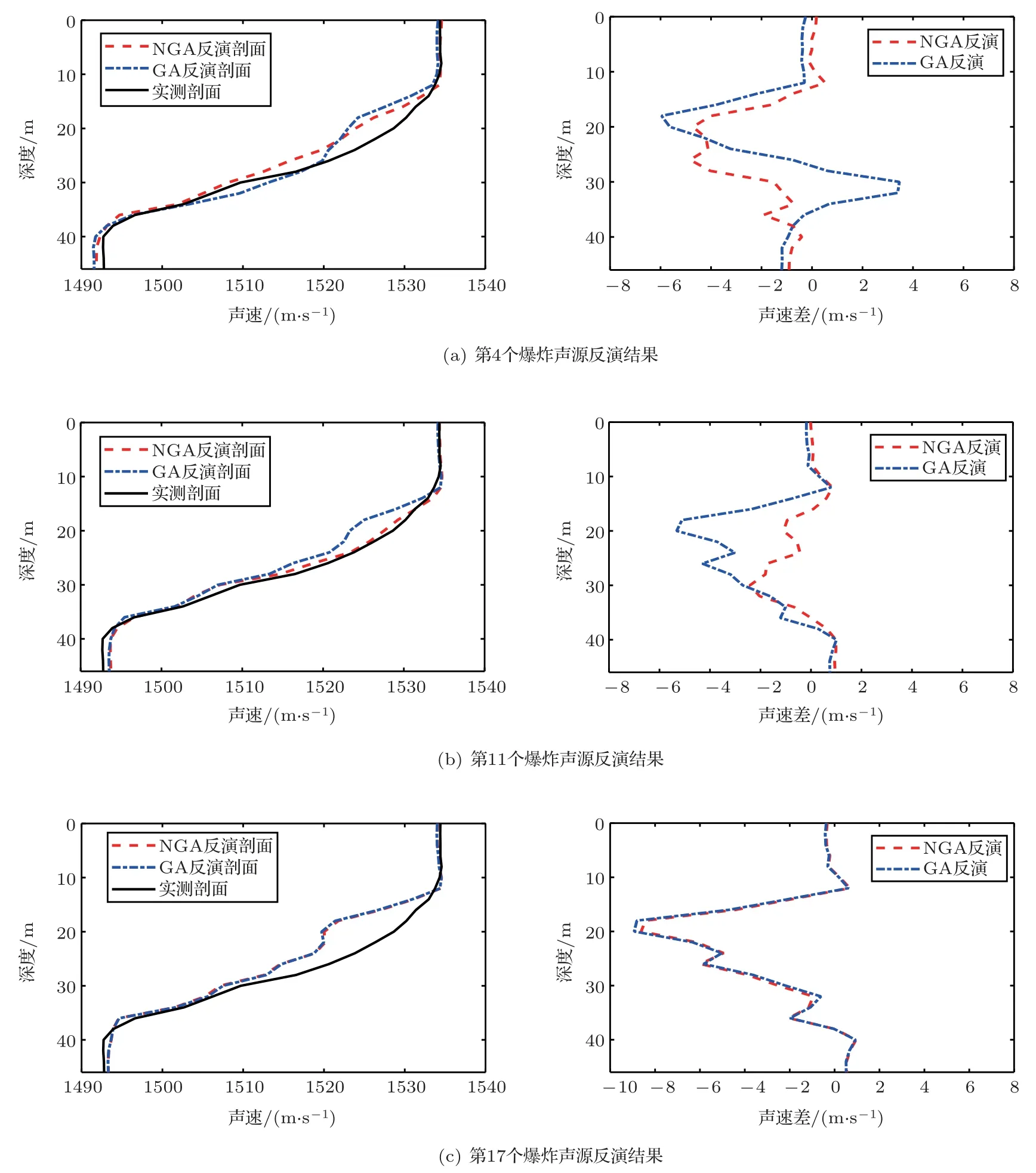
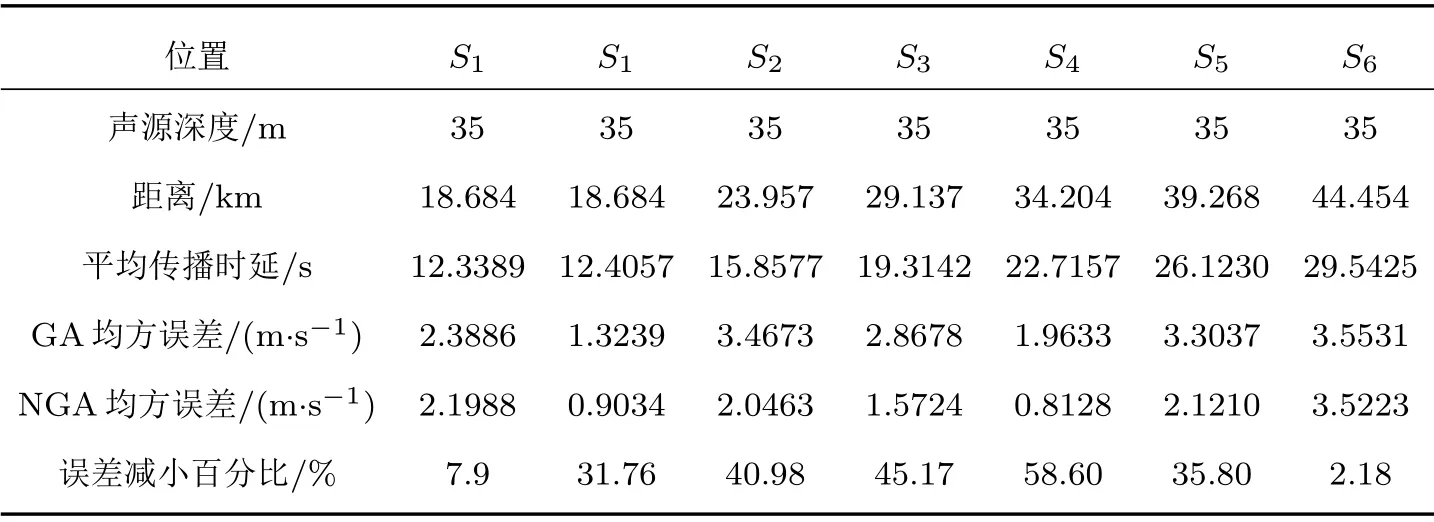
(2)對群體進行排序,記錄適應度Fi高的前N(N (3)與常規遺傳算法類似,對種群中的所有個體進行選擇、交叉、變異等操作; (4)將第2 步得到的N個個體和種群繁衍后的M個個體合并為一個新種群,計算新種群中的個體Xi之間的海明距離: 其中,xik為Xi的第k個變量。若||Xi ?Xj|| < L,則另對適應度小的個體(假定為Xi)適應度減半,Finew=0.5Fi; (5)判定終止條件,若滿足則輸出結果,否則再次對群體適應度排序,選取前M個個體組成新的種群返回第2步。 綜合經驗正交函數與小生境遺傳算法對淺海負躍層聲速剖面進行反演,具體步驟為 (1)基于海洋-聲學耦合模式提取海試位置歷史數據,結合處理后的實測聲速剖面作為樣本群計算經驗正交函數,并獲取經驗正交函數系數范圍; (2)依據經驗正交函數系數范圍和設定的運算精度,計算染色體長度,產生初始種群; (3)計算種群適應度,進行選擇、交叉、變異等一系列遺傳過程處理,以及小生境分析得到新的種群,重復以上操作; (4)達到設定的最大代數時或退出條件下,結束遺傳處理,通過最優染色體得到對應的經驗正交系數,從而獲得聲速剖面反演值。 代價函數是觀測物理量與拷貝物理量之間匹配關系的量化函數,考慮淺海環境的復雜性以及多途分離不明顯的情況,本文用聲傳播時長作為觀測信息構造如下代價函數: 其中,ti為各水聽器接收到最快特征聲線傳播時間的計算值,是拷貝物理量,拷貝量的計算是采用Bellhop聲場計算模型;τi是海試過程中各水聽器接收到最快特征聲線傳播時間的觀測值,是觀測物理量。聲速剖面反演流程如圖1所示。 圖1 聲速剖面反演流程Fig.1 The processing of sound speed profile invsersion 海上實驗于2019年8月在青島外海海域進行,海區深度約40 m。實驗過程中由發射船投放定深爆炸聲源,發射船、接收船同步接收聲信號,獲取聲傳播時長。在接收船左舷后甲板位置處懸掛一條陣深5~33 m、間隔2 m 的15元水聽器垂直陣,采集爆炸聲源信號。發射船由S1點(與接收船約10 n mile)航行至S6點(約22.5 n mile),每隔2.5 n mile各投放3 枚定深爆炸聲源(爆炸深度分別為7 m、25 m 和35 m);發射船于投彈前停航,船尾垂放一枚定深10 m的標準水聽器接收爆炸聲源信息,并通知接收船做好信號接收準備,于船頭投放定深爆炸聲源。發射船和接收船分別利用“多通道水聲信號同步采集系統”進行爆炸聲源信號采集,該系統由于嵌入GPS 模塊,可在采集水聲信號的同時獲取當前位置的GPS時鐘信息和位置信息,從而實現爆炸聲源的信號同步。實驗示意圖如圖2所示。 圖2 實驗過程示意圖Fig.2 The sketch map of experiment 利用發射船的10 m 標準水聽器和接收船的15元水聽器陣,結合“多通道水聲信號同步采集系統”軟件記錄對爆炸聲源信號進行處理。“多通道水聲信號同步采集系統”獲取的同步GPS 信息,可獲得接收信號的位置和時間信息,利用兩船接收信號時間差即可計算出聲信號在兩船之間的傳播時延。 實驗時,由于海況較差風浪較大,船舷拍打海面聲音較大,這里選取各點定深35 m爆炸聲源信號進行分析。實驗期間由兩船聽測的爆炸聲源信號分別如圖3、圖4所示,圖3為發射船水聽器接收的6枚定深35 m爆炸聲源信號局部放大圖;圖4為接收船水聽器陣分別接收的S1、S5兩點定深35 m 爆炸聲源信號局部放大圖,圖中分別示出7 m、15 m、27 m 和33 m四個水聽器信號。根據接收船接收信號的第一個波峰對應時刻和發射船接收信號脈沖對應時刻,即可計算出爆炸聲在兩船之間傳播時延。實驗用船為中國科學院海洋研究所“創新2 號”,船長47 m。實驗過程中舷側投擲定深彈,船尾吊放水聽器,兩者之間距離約為30 m。考慮到海區0~15 m 為均勻層,聲速1535 m/s,則需對時延另加0.0195 s。 圖3 定深35 m 爆炸聲源在發射船處的接收信號(第一幅圖中橫坐標“時間1308”意為13 點08 分,其他同理)Fig.3 The signal of 35 m explosion received at the launching ship (“1308” in the first fig means the time is 13:08, other similarities) 圖4 定深35 m 爆炸聲源接收船處接收信號Fig.4 The signal of 35 m explosion received at the receiving ship 結合前述得到的各投彈時刻兩船位置信息、接收信號精確的時間信息,可得到爆炸點及接收點的距離和聲傳播時延,如表1所示。 表1 投彈爆炸深度與發射接收船距離Table 1 Distance between the bomb and receiving ship 利用本次實驗獲取的定深爆炸聲源聲傳播時延數據對海區聲速剖面進行反演。海試過程中船載溫鹽深儀(Conductivity, temperature, depth,CTD)設備和聲速記錄儀(Sound velocity profile,SVP)測量得到的聲速剖面數據如圖5所示,其中藍色線為各實測剖面,黑色粗線為平均剖面。依據海洋-聲學耦合模式[16],結合所測聲速剖面作為經驗正交函數的樣本場,根據前述的經驗正交函數分解可得到3階EOFs函數如圖6所示。 圖5 實測聲速剖面Fig.5 Measured sound velocity profile 圖6 經驗正交函數Fig.6 Empirical orthogonal functions 采用圖1所示反演流程,對7 枚定深35 m 爆炸聲源進行聲速剖面反演。反演過程中,設定初始種群數為500,最大遺傳代數為40 代,交配概率為0.5,變異概率為0.2,運算精度為0.00001,選定種群數量的1/5 進行小生境實現,反演結果部分如圖7所示,整體統計結果見表2。 圖7 聲速剖面反演結果與實測數據對比Fig.7 Comparison of inversion results of sound velocity profile with measured data 表2 聲速剖面反演結果統計Table 2 Statistics of sound velocity profile inversion results 圖7中僅列舉3 類比較常見的反演結果對比情況:圖7(a)對應NGA算法結果相比于常規GA算法精度有顯著提高,該情況在35 m 聲源的7 次實驗中出現2 次;圖7(b)對應反演精度大幅提高的情況,該情況出現3 次;圖7(c)對應為兩種反演方法精度基本一致,該情況出現2 次。由反演結果可知,反演誤差較大的位置處于溫躍層深度。分析認為本文的研究方法是在海區水聲環境水平和時間分布均勻的前提下展開,現場測試所得聲速剖面集合中各點的聲速剖面在溫躍層差異大,反演結果與實測情況基本相同。另外通過分析算法中每一代的最優解可知,在前兩種情況中,常規遺傳算法均出現“早熟”,即收斂到局部最優解的現象。在爆炸聲源35 m 的7 次實驗(序號分別為2、4、7、9、11、14、17)中,NGA算法反演均方根誤差平均為1.88 m/s,其中最小的均方根誤差為0.81 m/s,可得NGA 算法能夠有效反演聲速剖面。另外,NGA 算法相比于傳統GA 算法的均方根誤差平均減少35.5%,即NGA算法相比于常規遺傳算法更為精確。 結論適用于本次海試中其他爆炸深度的實驗結果,由于篇幅原因不再展開。 采用小生境遺傳算法研究聲層析聲速剖面的反演問題,基于經驗正交函數降低反演參數維度,結合海洋-聲學耦合模式和2019年青島外海聲傳播實驗數據構建基礎樣本庫,利用小生境遺傳算法和常規遺傳算法對處理后的爆炸聲傳播數據進行淺海負躍層環境下的聲速剖面反演。小生境遺傳算法反演均方根誤差最小為0.81 m/s,平均均方根誤差1.88 m/s,說明小生境算法能夠有效進行淺海負躍層環境下反演聲速剖面。另外,對比反演結果,小生境遺傳算法較常規遺傳均方根誤差平均較少約35%,算法精度顯著提高。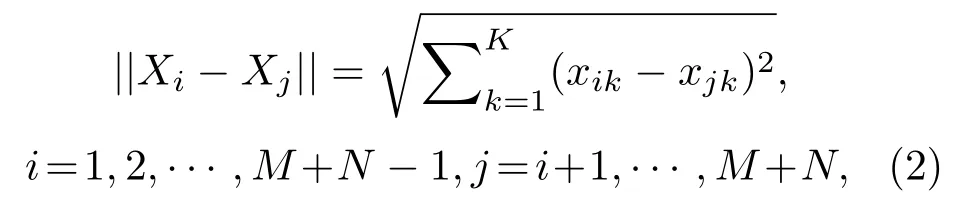
2 反演模型
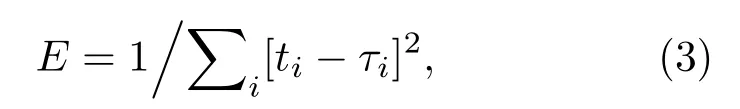
3 實驗驗證
3.1 實驗概況
3.2 信號處理

3.3 聲速剖面反演
4 結論

