短圓管換能器輻射阻抗

梁家寧 莫喜平 柴 勇 劉永平

(1 中國科學院聲學研究所 北京 100190)

(2 中國科學院大學 北京 100049)

(3 北京海洋聲學裝備工程技術研究中心 北京 100190)

0 引言

圓管換能器由于其結構簡單、性能可靠、聲輻射面積大、輻射效率高等優點，在水聲及超聲領域有廣泛應用。Morse[1]最早研究圓柱體聲輻射問題，基于柱坐標系下的聲波方程給出了圓柱體輻射聲場和格林函數的表達式。Junger 研究了速度在軸向均勻分布以及在軸向和周向周期性變化的無限長圓柱的輻射阻抗[2]，并推導了簡諧力作用下無限長彈性殼體表面的位移和流體中的聲壓分布[3]。Robey[4]基于格林函數推導了圓管均勻振動的自輻射和相互輻射阻，并討論了圓管之間的距離對輻射阻的影響。Greenspon 等[5]研究了無限長剛性圓柱體上矩形活塞的聲壓和互輻射阻抗，并對平面、球體和圓柱體上的活塞的互輻射阻抗進行了比較。Sandman[6]研究了兩端有剛性固定端面支撐的有限長圓柱殼體的輻射阻抗，在計算有限長圓柱殼流體負載時，可以用無限長剛性障柱上的圓柱殼體模型來近似。Steppanishen[7]研究了引入殼理論的彈性圓柱殼輻射阻抗的漸進表達式，并討論了不同振動模式對聲輻射的相互耦合效應。Bulter等[8]建立了剛性擴展模型，利用傅里葉級數法計算了0～2階圓管圓周模態的輻射阻抗。當圓管高徑比h/r >2時，利用剛性擴展模型可以較好地表述圓管換能器的輻射阻抗，但隨著高徑比(h/r)的減小，模型計算的輻射阻抗與實際存在較大誤差，因此，有必要對短圓管情況下(1h/r2)的輻射阻抗進行更精確的估計。

1 圓管換能器有限元分析

對圓管換能器建立有限元軟件二維軸對稱模型，如圖1所示。換能器為空氣背襯，上下兩端面處為剛性端蓋。為了簡化處理，建模過程中忽略剛性端蓋和去耦墊，代之以流體介質的剛性邊界條件。h為圓管換能器高度，r為圓管換能器半徑，在換能器半徑方向施加法向振速u。進行諧響應分析，提取表面節點壓強p(h)，根據公式(1)，計算流體反作用力并得到輻射阻抗，分析范圍kr= 0.03～10，結果如圖2、圖3所示。

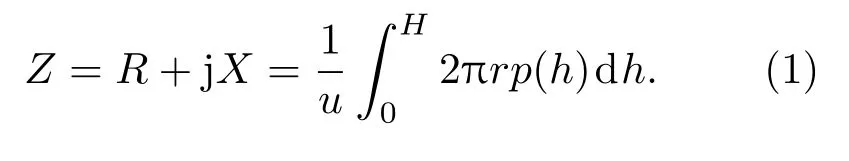
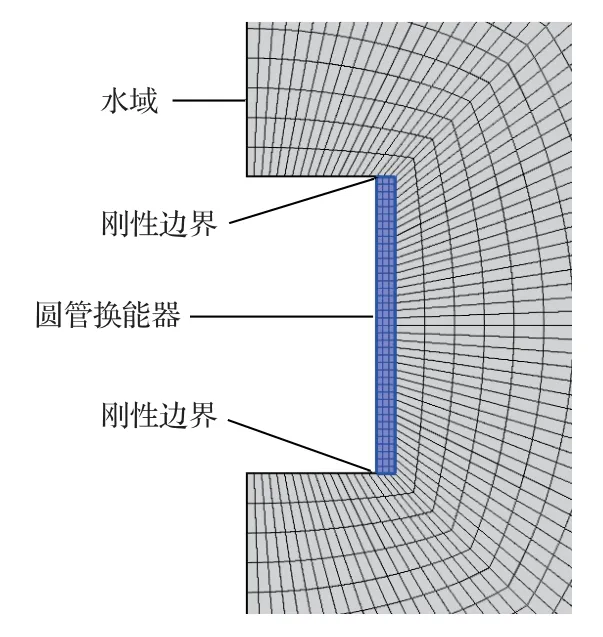
圖1 圓管換能器有限元模型Fig.1 Finite element model of a cylindrical transducer

如圖2、圖3所示，圓管換能器的輻射阻抗與圓管換能器高徑比(h/r)有關，且曲線的變化規律較復雜。隨著高徑比(h/r)的增加，在kr尺度較小時(kr <4)，輻射阻抗斜率變大；在kr尺度較大時(kr4)，輻射阻抗波動起伏減小。

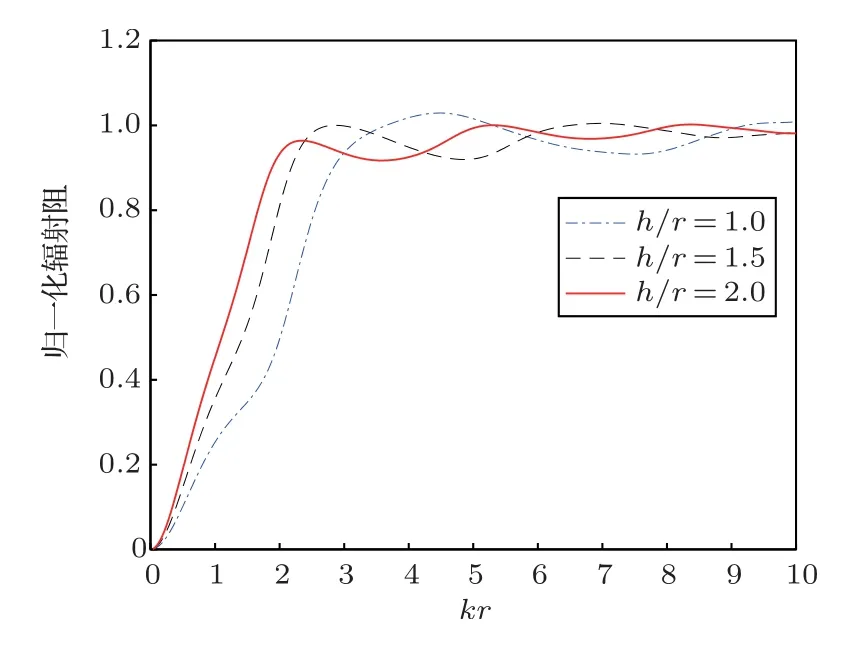
圖2 有限元計算輻射阻Fig.2 Finite element calculation results of radiation resistance

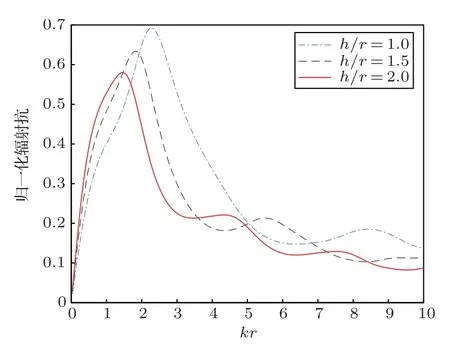
圖3 有限元計算輻射抗Fig.3 Finite element calculation results of radiation reactance

2 圓管換能器輻射阻抗的曲線擬合

由于圓管聲場瑞利積分求解的復雜性，想直接得到圓管換能器輻射阻抗的解析解是很困難的[9?10]。因此，提出一種圓管輻射阻抗經驗公式的表達形式。為了確定經驗公式的母函數形式，仔細研究圖2、圖3中曲線，發現其具有以下特點：(1)輻射阻抗受兩因素影響，分別是圓管的高徑比(h/r)和波數k。因此，母函數中應帶有兩自變量；(2)曲線存在漸進特性，輻射阻的漸進值R∞=ρcS，輻射抗的漸進值X∞= 0；(3)曲線存在振蕩特性，且振蕩幅度呈衰減規律；(4)曲線在kr較小時的增長趨勢類似于脈動球源的輻射阻抗曲線。

根據以上特點，選擇處理方法和函數類型：(1)設經驗公式的兩自變量為kh、kr；(2)漸進特性：將參量減去漸進值，作為新變量參與曲線擬合；(3)振蕩特性及衰減規律：用sinc 函數進行擬合；(4)設定母函數時參考脈動球源輻射阻抗公式。

(1)歸一化輻射阻經驗公式為

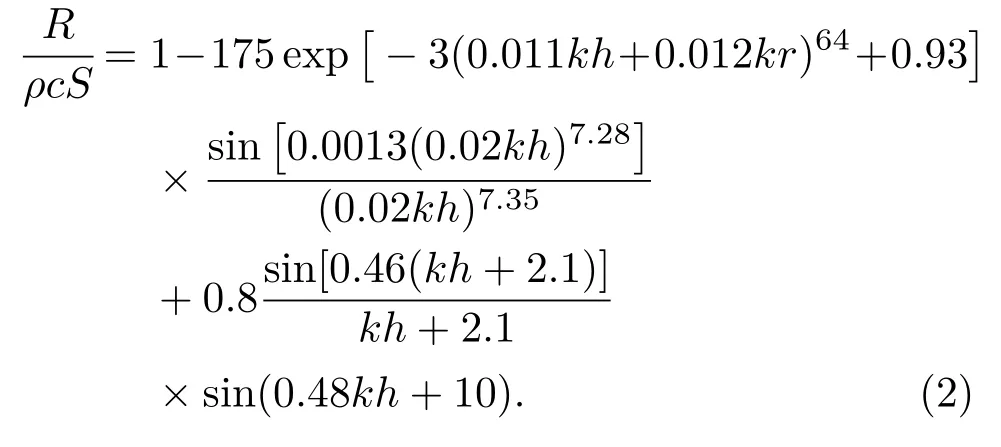
(2)歸一化輻射抗經驗公式為

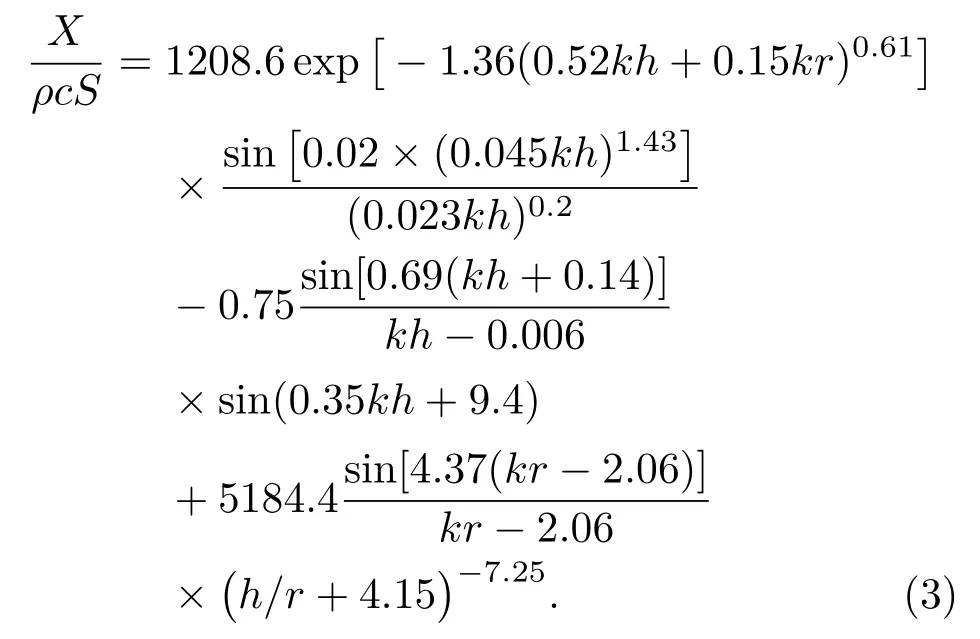
3 輻射阻抗經驗公式模型有效性驗證

為了估計圓管換能器輻射阻抗，Bulter 提出了圓管剛性擴展模型。聲場的瑞利積分可近似考慮成傅里葉級數的疊加，得到的輻射阻抗公式為[8]

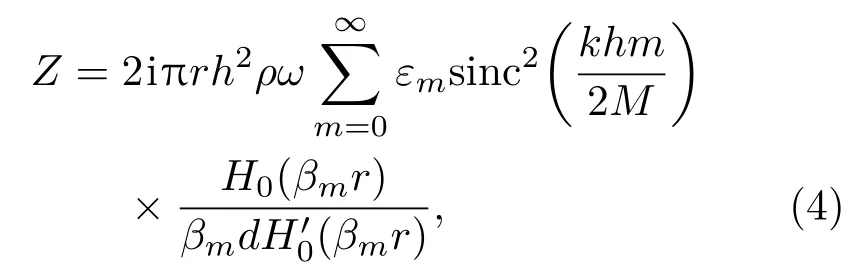
其中，βm=k[1?(m/M)2]1/2，M=d/λ，d為間距。

下面，選取高徑比h/r=1、h/r=1.5、h/r=2三組數據對比分析經驗公式與剛性擴展模型計算輻射阻抗結果。

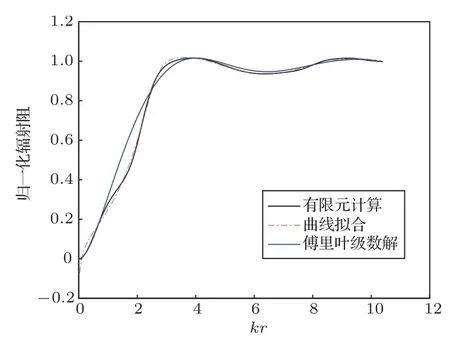
圖4 h/r =1，輻射阻計算方法對比Fig.4 Comparison of radiation resistance calculation results when h/r =1

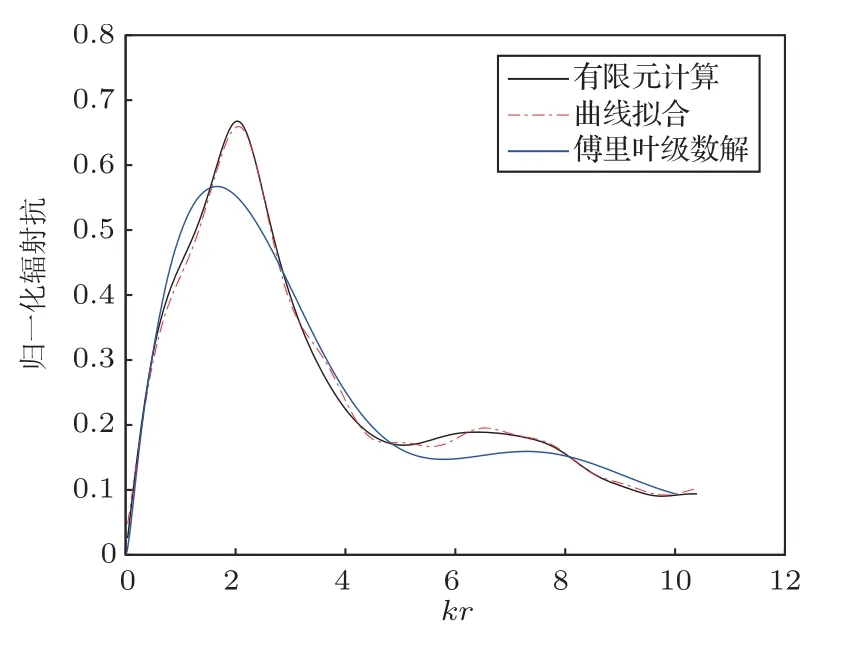
圖5 h/r =1，輻射抗計算方法對比Fig.5 Comparison of radiation reactance calculation results when h/r =1

由圖4～圖9對比可以看出，在1h/r2 的范圍內，經驗公式計算得到的輻射阻抗與有限元結果較為相符，擬合程度較高。隨后計算曲線擬合、傅里葉級數解與有限元計算得到的輻射阻抗的擬合系數，如表1、表2所示。曲線擬合的擬合系數在3種高徑比情況下均大于0.998，而傅里葉級數解擬合系數均不超過0.99，這是由于剛性擴展模型為理想模型，在較低高徑比下存在剛性壁面的反射，導致計算結果與有限元結果出現誤差。

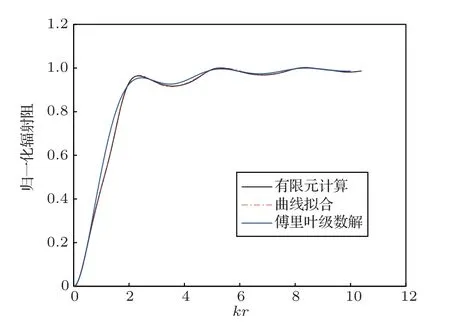
圖6 h/r =1.5，輻射阻計算方法對比Fig.6 Comparison of radiation resistance calculation results when h/r =1.5

圖7 h/r =1.5，輻射抗計算方法對比Fig.7 Comparison of radiation reactance calculation results when h/r =1.5

表1 曲線擬合、傅里葉級數解與有限元計算輻射阻的擬合系數(1 h/r 2)Table 1 Fitting parameters between curve fitting, Fourier series solution and finite element calculation of radiation resistance(1 h/r 2)

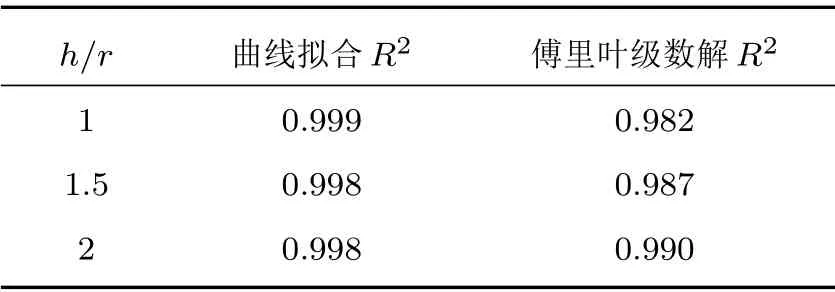
表1 曲線擬合、傅里葉級數解與有限元計算輻射阻的擬合系數(1 h/r 2)Table 1 Fitting parameters between curve fitting, Fourier series solution and finite element calculation of radiation resistance(1 h/r 2)

h/r 曲線擬合R2 傅里葉級數解R2 0.999 0.982 1.5 0.998 0.987 2 0.998 0.990 1

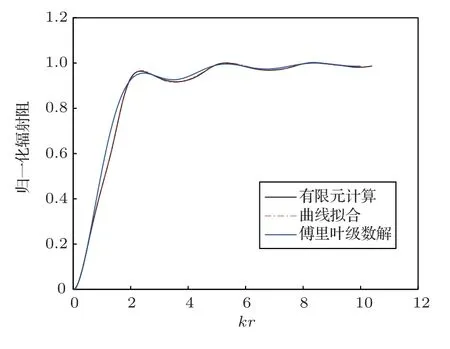
圖8 h/r =2，輻射阻計算方法對比Fig.8 Comparison of radiation resistance calculation results when h/r =2

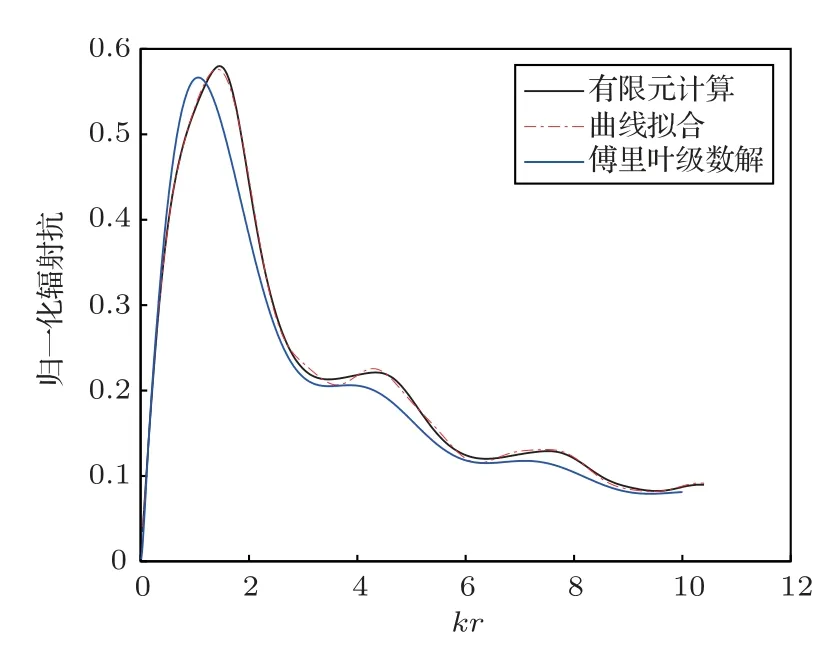
圖9 h/r =2，輻射抗計算方法對比Fig.9 Comparison of radiation reactance calculation results when h/r =2

表2 曲線擬合、傅里葉級數解與有限元計算輻射抗的擬合系數(1 h/r 2)Table 2 Fitting parameters between curve fitting, Fourier series solution and finite element calculation of radiation reactance(1 h/r 2)

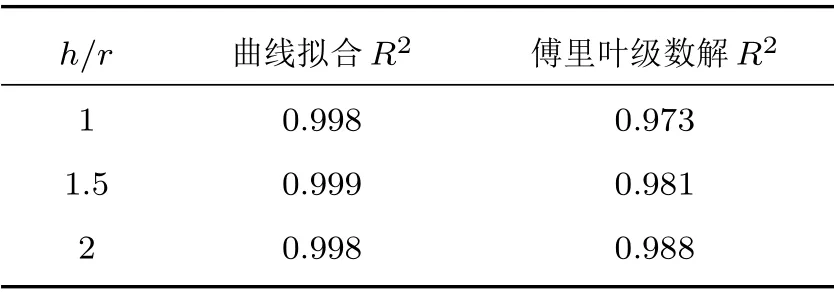
表2 曲線擬合、傅里葉級數解與有限元計算輻射抗的擬合系數(1 h/r 2)Table 2 Fitting parameters between curve fitting, Fourier series solution and finite element calculation of radiation reactance(1 h/r 2)

h/r 曲線擬合R2 傅里葉級數解R2 0.998 0.973 1.5 0.999 0.981 2 0.998 0.988 1

當圓管高徑比進一步減小時(0.8h/r1)，計算曲線擬合、傅里葉級數解與有限元計算得到的輻射阻抗的擬合系數，如表3、表4所示。隨著圓管高徑比的不斷減小，經驗公式模型與有限元計算結果誤差逐漸增大。曲線擬合的擬合系數在兩種高徑比情況下相較之前略有降低，但仍大于0.994，這是由于為了保證經驗公式的計算精度，h/r1 部分的數據未參與經驗公式擬合。然而當0.8h/r1時，傅里葉級數解擬合系數均小于0.98，計算結果與理論值相差較大。此時經驗公式相較于剛性擴展模型仍能較準確描述圓管換能器輻射阻抗。

表3 曲線擬合、傅里葉級數解與有限元計算輻射阻的擬合系數(0.8 h/r 1)Table 3 Fitting parameters between curve fitting, Fourier series solution and finite element calculation of radiation resistance(0.8 h/r 1)

表3 曲線擬合、傅里葉級數解與有限元計算輻射阻的擬合系數(0.8 h/r 1)Table 3 Fitting parameters between curve fitting, Fourier series solution and finite element calculation of radiation resistance(0.8 h/r 1)

h/r 曲線擬合R2 傅里葉級數解R2 0.8 0.994 0.973 0.9 0.996 0.978

表4 曲線擬合、傅里葉級數解與有限元計算輻射抗的擬合系數(0.8 h/r 1)Table 4 Fitting parameters between curve fitting, Fourier series solution and finite element calculation of radiation reactance(0.8 h/r 1)

表4 曲線擬合、傅里葉級數解與有限元計算輻射抗的擬合系數(0.8 h/r 1)Table 4 Fitting parameters between curve fitting, Fourier series solution and finite element calculation of radiation reactance(0.8 h/r 1)

h/r 曲線擬合R2 傅里葉級數解R2 0.8 0.998 0.967 0.9 0.998 0.970

4 結論

由于圓管換能器的輻射阻抗隨圓管半徑、高度和波數而變化，因此輻射聲場很難用解析解表達。為解決這一問題，采用有限元分析法計算了圓管換能器的輻射阻抗，并根據計算結果擬合得到了經驗公式。通過將剛性擴展模型和經驗公式模型的結果與有限元數據進行比較，可以確定當短圓管情況下(1h/r2)，經驗模型的精度在誤差允許范圍內。同時，當圓管高徑比在0.8～1范圍內，經驗公式只存在較小的誤差。因此，當圓管換能器的高徑比較小時，經驗公式模型可以更準確地描述輻射阻抗。這不僅有助于研究圓管換能器的輻射功率和效率，而且有助于進一步優化結構。同時，為類似難以用解析解表達的問題提供借鑒思路。