用于三維散射中心SBR建模的邊緣繞射修正

陸金文，閆 華，殷紅成，張 磊，董純柱

(北京環境特性研究所 電磁散射重點實驗室，北京 100854)

在高頻區，雷達目標總的電磁散射可以由多個局部散射源的響應相干合成，這些局部散射源被稱為散射中心[1]。這些散射中心通常都與特定的散射機理相對應，如鏡面反射、邊緣繞射等。散射中心的參數化模型具有形式簡單、稀疏以及與散射機理和目標屬性相關等優點，廣泛應用于高分辨成像[2-4]、數據壓縮與重建[5-7]、雷達目標識別[8-11]等領域。與一維、二維情形相比，三維散射中心模型更能完整描述目標散射中心的空間分布，研究目標三維散射中心建模方法具有重要的學術和應用價值。

基于電磁仿真計算的散射中心建模主要包括逆向方法和正向方法。逆向建模是在已知散射數據和確定模型形式的條件下實現模型參數反演的方法[12-15]，通常需要計算大量的掃頻、掃角雷達截面積(Radar Cross Section，RCS)幅相數據，計算效率不高。而正向建模方法充分利用目標的精確幾何知識和電磁散射機理來確定模型參數[16-23]，在計算效率方面有較大優勢。文獻[16]在彈跳射線(Shooting and Bouncing Ray，SBR)技術的基礎上推導了圖像域射線管積分(Image Domain Ray Tube Integration，IDRTI)公式，能夠在點頻、單視角下快速生成目標的三維逆合成孔徑雷達(Inverse Synthetic Aperture Radar，ISAR)圖像，并利用迭代峰值搜索算法在ISAR像中提取目標的三維散射中心。文獻[17]通過調整ISAR像生成公式中射線擴散函數的形式，在不增加計算復雜度的情況下能夠提高ISAR像的質量，減少散射中心的提取時間。文獻[18]也提出一種基于彈跳射線技術的海面艦船目標三維散射中心快速建模方法，利用提取的散射中心能夠重建精度較高的一維距離像和二維ISAR像。朱國強等人率先提出了基于部件分解與射線分集的屬性散射中心參數正向推算方法[19]，并陸續實現了三維散射中心位置的精確修正[20]和正向建模的自動化處理[21]。盡管如此，由于上述基于射線追蹤的散射中心建模方法只考慮了目標的物理光學(Physical Optics，PO)貢獻，而物理光學無法描述真實邊緣繞射的貢獻，故針對邊緣繞射形成的散射中心，基于這些方法獲得的模型存在較大的誤差。另外，LI等人[22]提出了基于全波法計算的感應電流分布的散射中心建模方法，BUNGER[23]也利用全波法實現了目標的三維ISAR像快速生成和散射中心提取。盡管上述基于全波法的散射中心建模方法能夠精確計算邊緣繞射形成的散射中心的模型參數，但其計算效率不高，且難以解決多次散射機理的散射中心建模問題。

針對上述問題，綜合考慮目標鏡面反射與邊緣繞射的貢獻，將IDRTI和等效邊緣電磁流(Equivalent Edge Currents，EEC)方法相結合，提出了一種針對基于彈跳射線技術的三維散射中心建模的邊緣繞射修正方法。針對立方體、圓柱體、球頭錐和帶尾翼的球頭錐-圓柱-圓臺組合體(帶翼組合體)四類導體目標，進行了實驗。實驗結果表明，該方法能夠有效提高三維散射中心的提取精度。

1 基于IDRTI技術的三維散射中心提取方法

在平面波入射情況下，根據物理光學方法，目標表面遠區散射電場可表示為

(1)

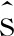
彈跳射線是一種標準的射線追蹤技術，廣泛用于高頻區復雜目標的電磁散射計算[24]。彈跳射線技術的主要步驟是首先向目標區發射大量平行射線，然后利用幾何光學原理追蹤并計算射線在目標表面彈射的路徑以及電磁場傳輸，最后利用上述物理光學公式計算出射點的散射貢獻。利用彈跳射線技術，將IDRTI公式三維擴展并改進后，YUN等人的三維ISAR像快速計算公式[17]為

(2)

其中，下標m表示射線的序號，*表示卷積運算，δ(·，·，·)表示三維狄拉克函數，z、x、y表示徑向距離和兩個正交的橫向距離，zm表示徑向的總距離延遲，橫向位置xm、ym為第一次和最后一次彈射點橫向位置的平均值，αm表示每根射線物理光學貢獻的復幅度值。h(x，y，z)為射線擴散函數，可表示為

h(x，y，z)=sinc(Δk·z)sinc(k0Δφ·x)sinc(k0Δθ·y) ，

(3)

其中，Δk、Δφ、Δθ表示波數帶寬和兩個橫向的角寬度。

獲得三維ISAR像后，利用CLEAN[25]算法可以提取目標的三維散射中心。CLEAN是一種迭代峰值搜索算法，通過逐次搜索殘余圖像中的峰值點來提取對應的散射中心，然后從圖像中剔除該散射中心的點擴散響應。假設第i次迭代提取的散射中心幅度和位置參數為Ai、(xi，yi，zi)，則殘余圖像可表示為

Ri+1=Ri-Aih(x-xi，y-yi，z-zi)。

(4)

2 用于三維散射中心建模的邊緣繞射修正方法

YUN等人的三維ISAR像計算公式(式(2))只考慮了目標的物理光學貢獻，筆者利用EEC方法對彈跳射線技術中的單次邊緣繞射貢獻進行修正，即

E=EPO+EEEC。

(5)

根據EEC方法，任意邊緣C的遠區繞射場可表示為

(6)

對于三角面元模型，邊緣C可以用若干根足夠短的直線段來逼近，式(6)中積分可以離散為照明區多段直邊緣的積分之和。在每小段直邊緣內，Ie和Im為常數，將其提到積分號外，則式(6)可簡化為

(7)

其中，

(8)

下標n表示每小段直邊緣的序號，rn、ln表示第n段直邊緣的中點位置矢量和長度。

ISAR像與遠區散射場之間存在傅里葉變換關系，對繞射場作三維傅里葉變換，則三維ISAR像可表示為

(9)

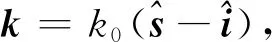
將式(7)代入式(9)，交換求和與積分運算的順序，可得

(10)

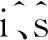
(11)

進一步求解積分，可得

sinc[Δk(z-zn)]sinc[k0Δφ(x-xn)]sinc[k0Δθ(y-yn)]}。

(12)

參考YUN方法[17]，將式(12)轉化為卷積形式，并與式(2)相結合，則最終考慮邊緣繞射修正的三維ISAR像計算公式為

(13)

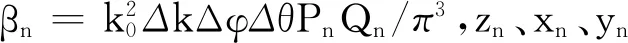
獲得考慮邊緣繞射修正的三維ISAR像后，同樣利用CLEAN算法(式(4))可以提取目標的散射中心，實現考慮邊緣繞射修正的三維散射中心建模。

3 實驗結果與分析

針對立方體、圓柱體、球頭錐和帶翼組合體四類導體目標，分別利用BHALLA方法[16]、YUN方法[17]和本文方法提取目標的三維散射中心，通過對比散射中心重建的與仿真的雷達截面積曲線及ISAR像來驗證本文方法的有效性。仿真法利用基于彈跳射線技術的高頻電磁軟件直接計算目標的雷達截面積數據。

立方體的幾何模型和雷達截面積曲線如圖1所示，尺寸為1 m×1 m×1 m。散射中心提取條件為：俯仰角90°、方位角0°～180°(1°間隔)、垂直-垂直極化、中心頻率10 GHz，ISAR空間三個方向的長度均為3 m，采樣點數均為64，計算ISAR像的帶寬為1 GHz，兩個角寬度均為6°，CLEAN算法的相對閾值(相對最強散射中心幅度下降)30dB。以仿真的雷達截面積為參考基準，BHALLA方法和YUN方法散射中心重建的雷達截面積均方根誤差為5.91 dB和4.97 dB，而本文方法的均方根誤差為0.97 dB。從圖1(b)中可看出，在方位角0°、90°和180°附近，立方體平面的鏡面反射為主要貢獻，BHALLA方法、YUN方法和本文方法散射中心重建的雷達截面積均吻合得較好。但隨著方位角逐漸偏離垂直鏡面方向，直邊緣繞射成為主要貢獻，BHALLA方法和YUN方法重建的雷達截面積存在較大偏差。

(a) 幾何模型

YUN方法和本文方法在方位角135°下的散射中心模型重建的ISAR像如圖2所示，兩幅ISAR像均能準確反映直邊緣散射中心的位置。YUN方法重建的ISAR像中直邊緣繞射強度分別為-6.21 dBsm、-12.54 dBsm和 -12.54 dBsm，而本文方法重建的ISAR像中對應直邊緣繞射強度為-2.07 dBsm、-19.72 dBsm 和 -19.72 dBsm，本文結果更符合立方體的直邊緣繞射機理。雷達截面積曲線及ISAR像綜合對比結果表明，本文方法提取的散射中心能較好地描述立方體直邊緣的散射貢獻。

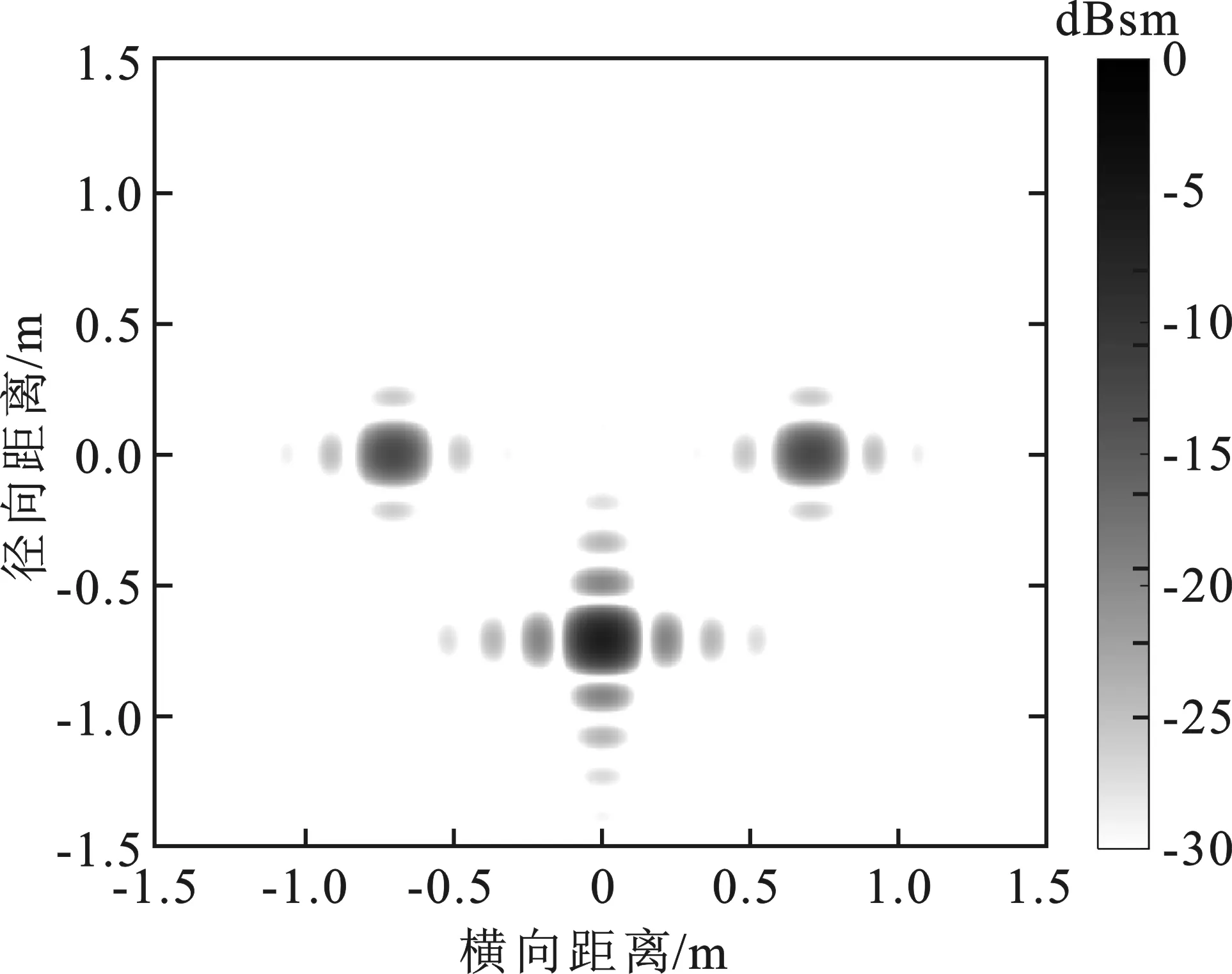
(a) YUN方法

圓柱體的幾何模型和雷達截面積曲線如圖3所示，尺寸為2 m×1 m×1 m。散射中心提取條件為：俯仰角90°、方位角0°～180°(1°間隔)、垂直-垂直極化、中心頻率10 GHz，ISAR空間三個方向的長度均為5 m，采樣點數均為128，計算ISAR像的帶寬為2 GHz，兩個角寬度均為12°，CLEAN算法的相對閾值為30dB。以仿真的雷達截面積為參考基準，BHALLA方法和YUN方法散射中心重建的RCS均方根誤差為6.67 dB和5.63 dB，而本文方法的均方根誤差為1.64 dB。從圖3(b)中可看出，在方位角0°、90°和180°附近，圓柱下底面、單曲面和上底面的鏡面反射為主要貢獻，BHALLA方法、YUN方法和本文方法重建的雷達截面積均吻合得較好。但隨著方位角逐漸偏離垂直鏡面方向，曲邊緣繞射成為主要貢獻，BHALLA方法和YUN方法重建的雷達截面積存在明顯偏差。

(a)幾何模型

YUN方法和本文方法在方位角135°下的散射中心模型重建的ISAR像如圖4所示，兩幅ISAR像均能準確反映曲邊緣散射中心的位置。YUN方法重建的ISAR像中曲邊緣繞射強度分別為-26.05 dBsm、-32.04 dBsm和-32.25 dBsm，而本文方法重建的ISAR像中對應曲邊緣繞射強度為-22.19 dBsm、-33.31 dBsm和-41.65 dBsm，本文結果更符合圓柱體的曲邊緣繞射機理。RCS曲線及ISAR像綜合對比結果表明，本文方法提取的散射中心能較好地描述圓柱體曲邊緣的散射貢獻。

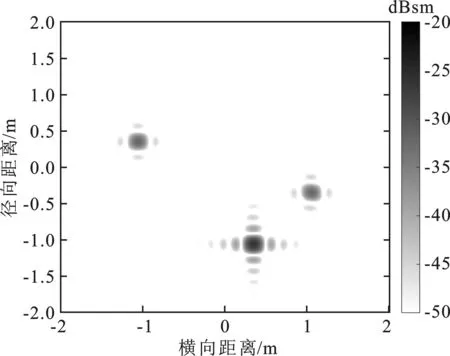
(a) YUN方法

球頭錐的幾何模型和雷達截面積曲線如圖5所示，尺寸為2.7 m×1 m×1 m。散射中心提取條件為：俯仰角90°、方位角0°～180°(1°間隔)、垂直-垂直極化、中心頻率10 GHz，ISAR空間三個方向的長度均為 6 m，采樣點數均為128，計算ISAR像的帶寬為2 GHz，兩個角寬度均為12°，CLEAN算法的相對閾值為 30 dB。以仿真的雷達截面積為參考基準，BHALLA方法和YUN方法重建的雷達截面積均方根誤差為 5.66 dB 和4.09 dB，而本文方法的均方根誤差為1.68 dB。從圖5(b)中可看出，在方位角90°～170°之間，球頭錐底面曲邊緣繞射為主要貢獻，BHALLA方法和YUN方法重建的RCS存在明顯偏差。

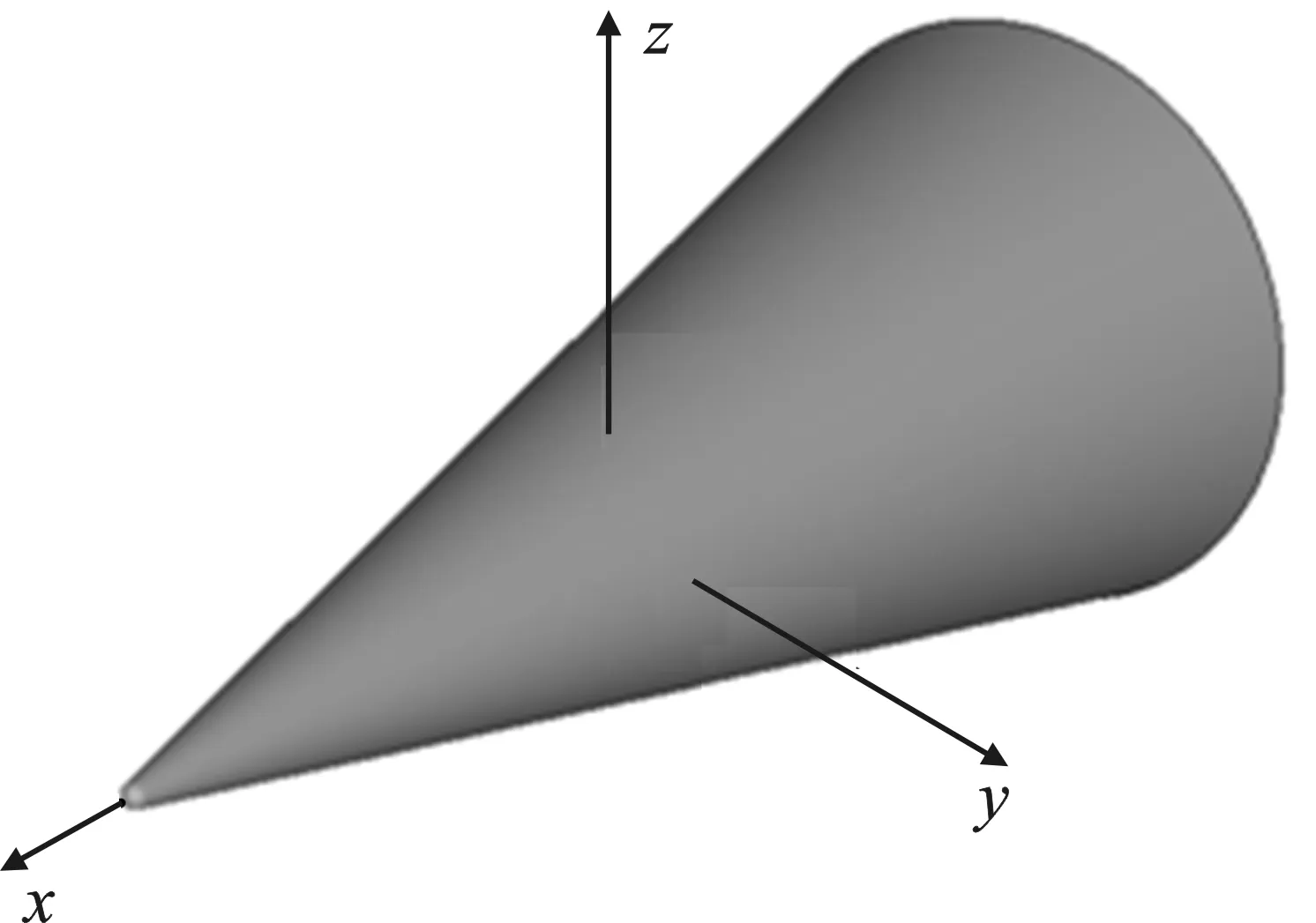
(a) 幾何模型

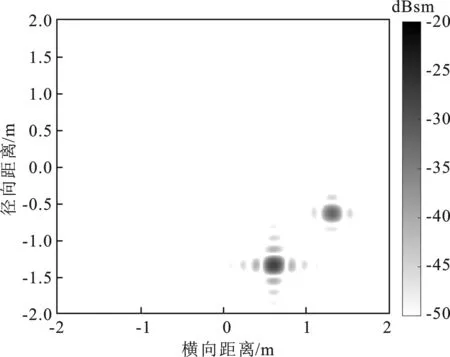
(a) YUN方法

YUN方法和本文方法在方位角135°下的散射中心模型重建的ISAR像如圖6所示。兩幅ISAR像均能準確反映曲邊緣散射中心的位置。YUN方法重建的ISAR像中曲邊緣繞射強度分別為-27.50 dBsm和-31.96 dBsm，而本文方法重建的ISAR像中對應曲邊緣繞射強度為-22.37 dBsm和-31.99 dBsm，本文結果更符合球頭錐的曲邊緣繞射機理。雷達截面積曲線及ISAR像綜合對比結果表明，本文方法提取的散射中心能較好地描述球頭錐曲邊緣的散射貢獻。

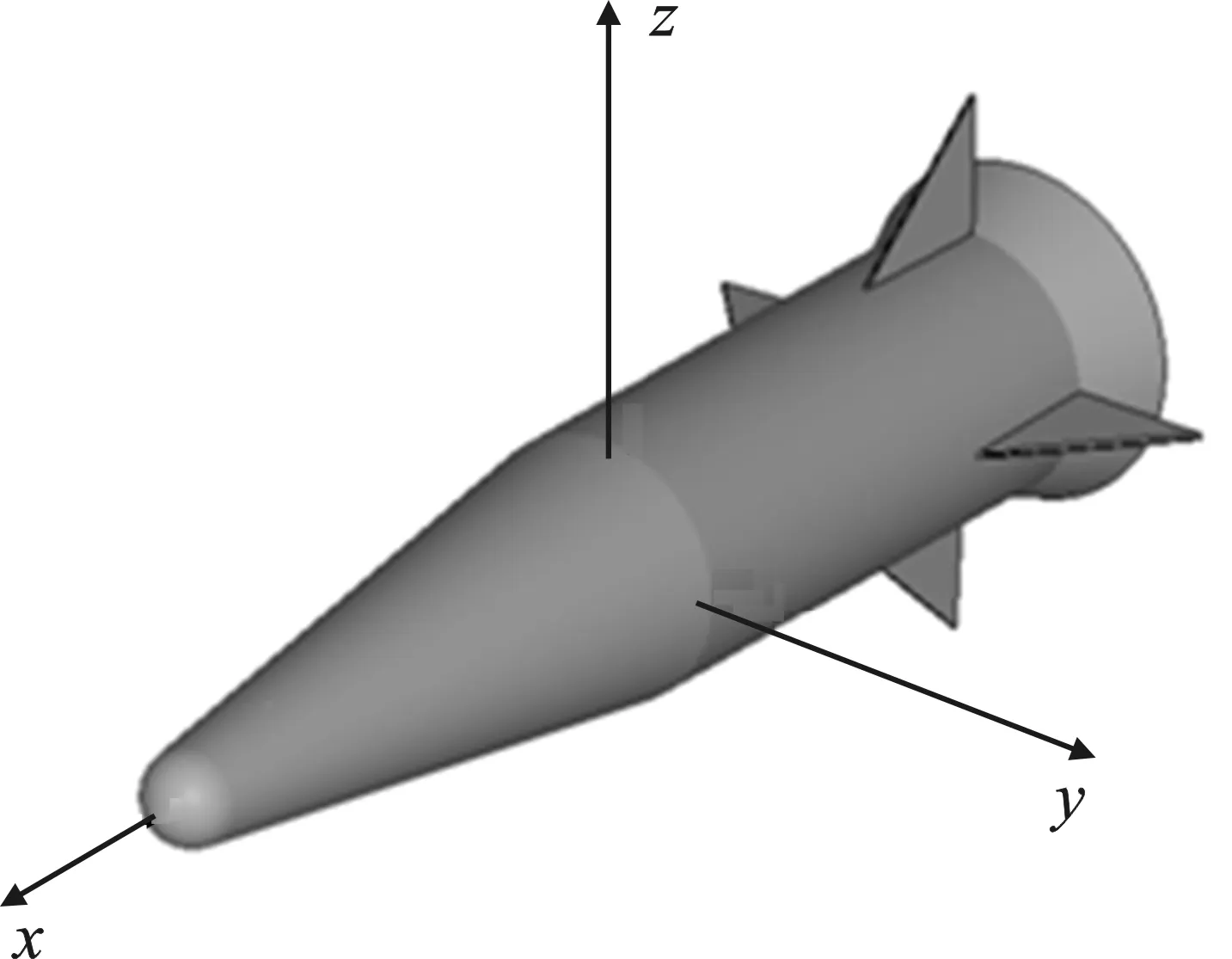
(a) 幾何模型

帶翼組合體的幾何模型和雷達截面積曲線如圖7所示，尺寸為4.2 m×1.6 m×1.6 m。散射中心提取條件為：俯仰角為90°、方位角0°～180°(1°間隔)、垂直-垂直極化、中心頻率10 GHz，ISAR空間3個方向的長度均為9 m，采樣點數均為192，計算ISAR像的帶寬為3 GHz，兩個角寬度均為18°，CLEAN算法的相對閾值為30 dB。以仿真的雷達截面積為參考基準，BHALLA方法和YUN方法重建的雷達截面積均方根誤差為4.33 dB和2.76 dB，而本文方法的均方根誤差為1.43 dB。從圖7(b)中可看出，在方位角90°～170°之間，尤其是140°～160°之間，帶翼組合體的尾翼和底面曲邊緣繞射為主要貢獻，BHALLA方法和YUN方法重建的雷達截面積存在明顯偏差。

YUN方法和本文方法在方位角135°下的散射中心模型重建的ISAR像如圖8所示，兩幅ISAR像均能準確反映尾翼和曲邊緣散射中心的位置。YUN方法重建的ISAR像中尾翼和曲邊緣繞射強度分別為-9.96 dBsm、-29.33 dBsm和-31.80 dBsm，而本文方法重建的ISAR像中對應邊緣繞射強度為-8.25 dBsm、-23.56 dBsm和-35.84 dBsm，本文結果更符合帶翼組合體的邊緣繞射機理。雷達截面積曲線及ISAR像綜合對比結果表明，本文方法提取的散射中心能較好地描述帶翼組合體邊緣的散射貢獻。

(a) YUN方法

針對四類目標，以仿真的雷達截面積為參考基準，BHALLA方法、YUN方法和本文方法提取的三維散射中心重建的雷達截面積均方根誤差如表1所示。從表1中可看出，與BHALLA方法和YUN方法相比，本文方法散射中心重建的四類目標雷達截面積的均方根誤差均顯著減小。四類目標散射中心重建的與仿真的雷達截面積曲線及ISAR像綜合對比結果表明，本文提出的用于三維散射中心建模的邊緣繞射修正方法可以更準確地表達目標的電磁散射特性，驗證了本文方法的有效性。

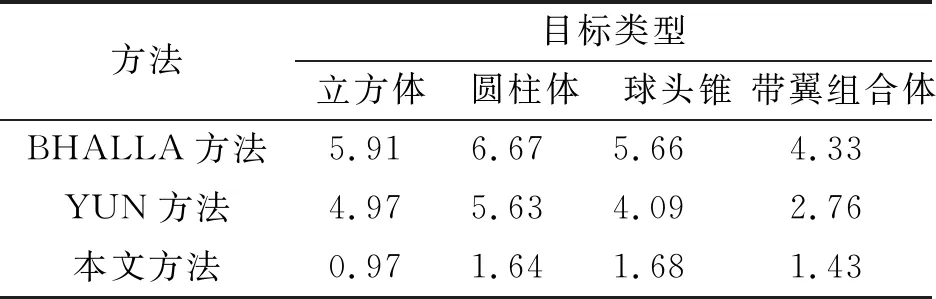
表1 BHALLA方法、YUN方法和本文方法散射中心重建的RCS均方根誤差 dB

4 結束語

筆者提出了一種針對基于SBR技術的三維散射中心建模的邊緣繞射修正方法。結合IDRTI技術和EEC方法，推導了考慮邊緣繞射修正的三維ISAR像計算公式。在生成的ISAR像基礎上，結合CLEAN算法，實現了目標的三維散射中心快速建模。針對立方體、圓柱體、球頭錐和帶翼組合體四類導體目標，以仿真的雷達截面積為參考基準，與BHALLA方法和YUN方法對比表明，基于該方法提取的散射中心模型重建的雷達截面積均方根誤差顯著減小。四類目標散射中心重建的與仿真的雷達截面積曲線及ISAR像綜合對比結果表明，本文方法能夠有效提高三維散射中心的提取精度，尤其對邊緣繞射影響較大的目標來說，可以實現更準確的電磁散射特性表達。