基于ASAPSO的火炮隨動系統模糊控制策略

王繼超, 冷育明, 戚延輝, 王 磊

中國人民解放軍31696部隊，遼寧 錦州 121000)

0 引 言

進入21世紀以來，交流伺服技術與智能控制相結合，使得永磁同步電機(PMSM)在各個領域得到了廣泛的應用。在速度控制和位置控制上，以PMSM為主的交流伺服系統已成為主流，在工業領域和軍事技術等方面均取得了突出的效益。當前，地面火炮控制系統仍采用直流有刷電機作為執行元件。從控制效果看，不僅響應速度慢，而且定位精度一般。因此，從提高武器裝備性能的角度出發，將交流伺服系統應用于火炮隨動跟蹤控制系統勢在必行。

PMSM作為執行元件，應用于火炮隨動系統上，必須適應隨動系統轉動慣量大、位置變化無規律、響應速度快、定位精度高的特點[1]。因此，位置控制器的設計要求必須高。

與常規PID控制方式相比，模糊控制算法并不需要對被控系統建立數學模型。PMSM具有非線性特點，作為火炮隨動系統執行元件時，常規的PID 控制方式難以跟隨系統變化，對火炮隨動跟蹤系統的控制達不到要求。而模糊控制器在解決這一問題時，效果大大優于PID控制器。

模糊控制器性能的好壞，主要取決于4個參數，分別為3個量化參數和1個模糊規則權值[2]。因此，為了保證火炮隨動跟蹤系統的速度和精度，本文采用自適應模擬退火粒子群算法(ASAPSO)對這4個參數進行優化。通過仿真，對比了模糊控制器和傳統PID控制器在火炮隨動跟蹤系統中的控制效果[3]。

1 系統結構

1.1 火炮隨動跟蹤系統基本模型

火炮隨動跟蹤系統由視頻跟蹤器、瞄準線控制器、執行機構和相應的傳感器組成。圖1為獨立穩定的瞄準線控制系統結構圖[4]。

圖1中，目標位置θi與瞄準線位置θo的差值送給視頻跟蹤器，x為跟蹤誤差，M為執行機構的控制力矩。其中，執行機構用來帶動火炮身管高低方向運動。系統采用PMSM替代傳統直流電機，是本文研究的重點對象。

1.2 控制系統結構和模型的建立

以PMSM替代傳統的無刷直流電機作為系統的執行機構，構建空間矢量模型。控制模塊采用dsPIC33F來實現空間矢量控制脈寬調制(PWM)[5]。搭建三閉環位置控制系統如圖2所示。

該隨動控制跟蹤系統的模型大致由以下5個模塊構成:

(1) 角度偏差傳感器模塊；

(2) PI調節器；

(3) 坐標變換模塊；

(4) 空間矢量PWM(SVPWM)模塊；

(5) 模糊控制器。

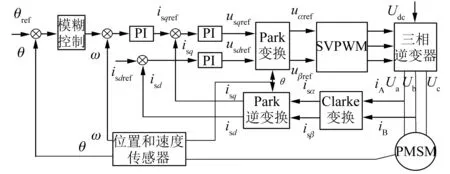
圖2 交流伺服系統三閉環矢量控制系統模型

控制過程為：目標位置與瞄準線位置的差值經視頻跟蹤器處理后得出跟蹤誤差x。模糊控制器放在系統位置環上，輸出速度信號。q軸電流分量由速度PI調節器調節誤差信號后得出，d軸電流分量為設定值零。q軸和d軸電流分量經坐標變換后,得到相電壓分量并通過SVPWM技術，產生PWM信號。控制IGBT模塊，逆變輸出可變頻率的三相正弦電壓輸入到電機定子,達到控制的目的[6]。

2 模糊控制器

2.1 模糊控制器的組成和原理

模糊控制系統的基本工作原理可以用圖3來表示。控制過程為：單片機對被測對象進行采樣并進行A/D轉換，與給定值進行比較，從而得到誤差e。誤差e經過模糊化處理后，代入已經制定好的模糊控制規則，做出模糊決策，輸出控制量u。圖中虛線框內的模糊控制器是核心部分，模糊控制規律可以通過計算機程序設定[7]。

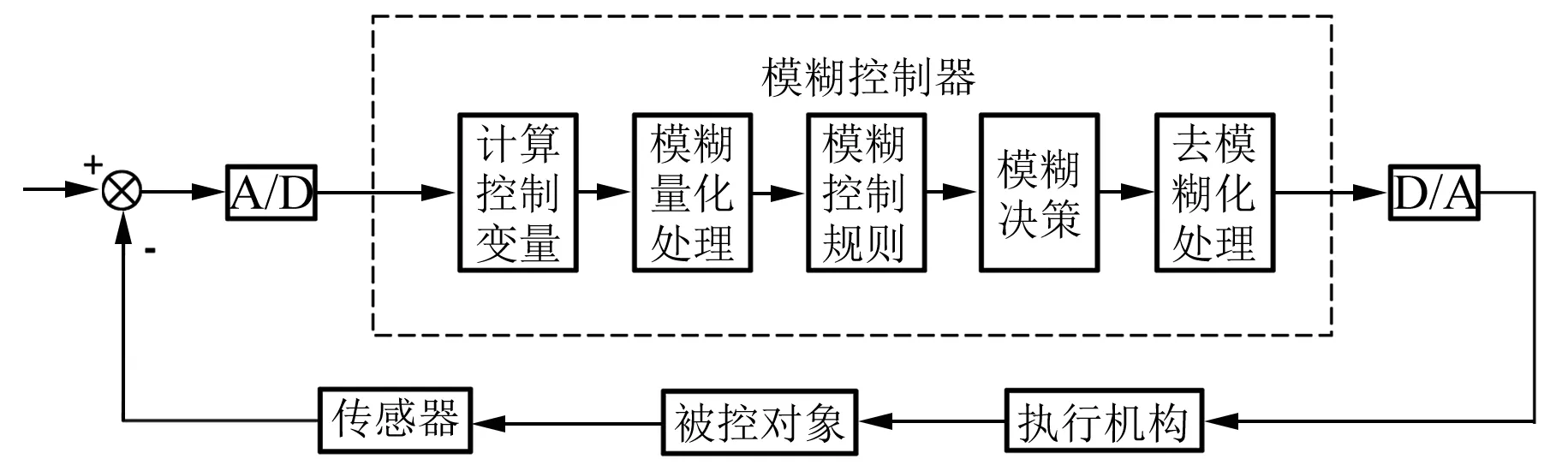
圖3 模糊控制系統原理圖

對于火炮隨動跟蹤系統，圖3中的被控對象就是火炮身管，執行機構采用PMSM，傳感器采用增量式編碼器。模糊控制器通過編寫程序設定在控制系統中。其主要由4個部分組成：模糊化接口、知識庫、模糊推理和去模糊化。

2.2 模糊控制器的設計

2.2.1 模糊化接口

將測得的目標實際位置和火炮瞄準線位置相比較，得到誤差信號e。該信號和變化量ec設定為2個輸入量，執行機構給出的身管轉動速度u作為輸出量。將誤差e、誤差變化率ec和轉速u進行尺度變換，統一采用歸一化處理，即e∈[-1，1]，ec∈[-1，1]，u∈[-1，1]。

輸入量e、ec和輸出量u的隸屬度函數選擇三角形隸屬度函數[8]。隸屬度函數形狀及配置均按圖4所示設置。為了更好地描述三角形分布特點，反映隸屬度函數的控制規律，引入間隔參數sp，間隔參數的大小反映的是三角形頂點的分布情況。當sp>1時，三角形向中間聚攏；當sp<1時，三角形向兩邊聚攏。圖4所示為sp=2時隸屬度函數的形狀。

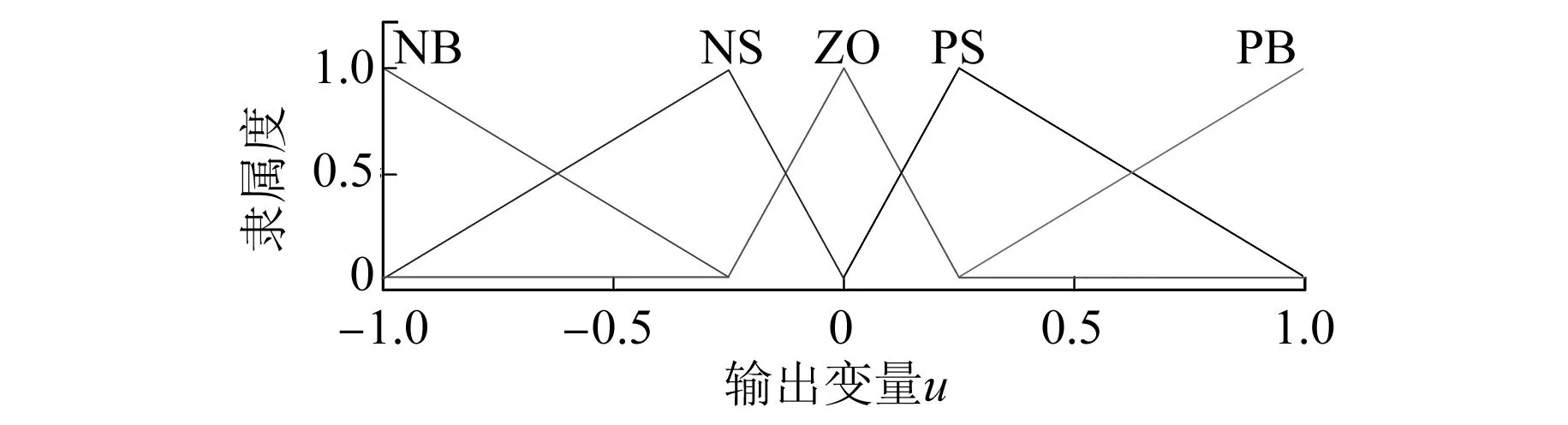
圖4 間隔參數為2時的隸屬度函數

作為輸入量，誤差和誤差變化率的量化因子分別為ke和kec，電機的轉速作為輸出其比例因子設定為ku。綜合考慮電機控制的精度和響應速度，e和ec均選擇了5個模糊子集(NB、NS、ZO、PS、PB)，控制量u選擇了7個模糊子集(增加了NM-負中和PM-正中2個子集)來覆蓋論域。

2.2.2 知識庫和模糊推理

知識庫當中存放的是各個輸入和輸出量在進行模糊化時設定的論域映射關系，以及設定的模糊子集個數。知識庫當中還應當建立語言規則庫，用來設定輸入輸出之間的關系，從而反映出控制規則。這些規則的制定是通過人的經驗和直覺用相應的語言描述出來的[9]。模糊控制規則如表1所示。該控制系統一共有25條模糊規則。

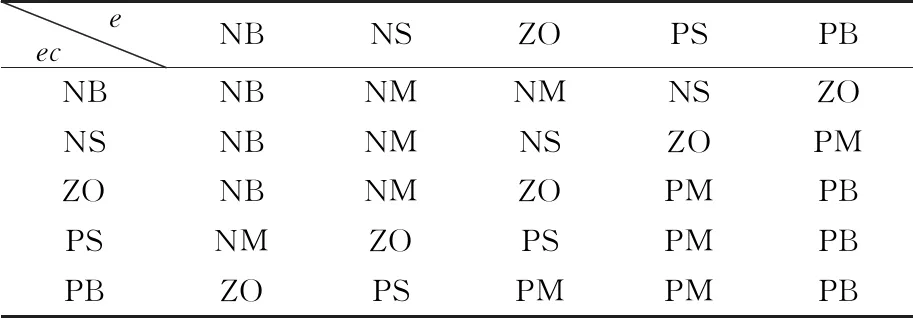
表1 模糊控制規則狀態

2.2.3 精確化計算

模糊量需要轉換為精確量才可以對系統進行控制。本文運用重心法將模糊量轉變成精確量，該方法將面積的重心作為推理結果。運用重心法解模糊的過程類似于加權平均法，其權值為各元素的隸屬度[10]。其計算式如下：

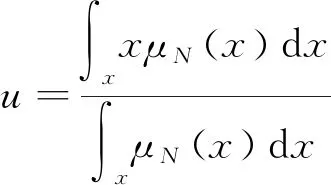
(1)

3 ASAPSO算法

3.1 模擬退火算法

模擬退火算法是受固體退火的原理啟發而形成的[11]。固體加溫的過程中，由于其內部粒子運動速度加快，內能不斷增大，當其達到一定的溫度后開始降溫，內部粒子由快速運動逐漸減慢，內能也逐步減小，粒子趨于穩定，最后在固體溫度達到穩定值常溫時，內能保持在穩定狀態即最小值。

其基本思想是：目標函數f的設定遵循的原則為尋求固體內能E的最小值，其中E為固體在溫度為T時的內能，不同T時內能的改變量為ΔE。算法由初始解i和溫度T演化的控制參數t開始，對當前解重復進行“生成新解—算目標函數差值—判斷是否接受”的迭代，t值不斷衰減，并在終了時得到近似的最優解。退火進程包含了給定初始溫度T開始、每個t值時刻的迭代次數k和停止條件S[12]。

基本流程：

(1) 給定初始溫度T開始(T充分大)及初始解狀態，每個t設定的迭代次數k，最低溫度T終止；

(2) 計算該點的適應值E=f(S)；

(3) 更新計算當前溫度t；

(4) 產生新解S′；

(5) 計算新解的適應值E′=f(S′)以及適應值增量ΔE=f(S′)-f(S)，如果滿足終止條件則停止算法。

3.2 ASAPSO算法優化模糊控制器原理

與標準PSO相比，自適應模擬退火粒子群算法在算法優化過程中能夠根據各個粒子的適應值主動調節學習因子，從而克服了局部收斂的問題[13]。在前一階段利用標準PSO算法尋求優化，以提高算法的運行速度，后一階段結合模擬退火算法，不斷優化更新參數并尋求最優解。

為了提高PSO算法解決全局優化問題的能力，鑒于ASAPSO 算法的尋優特點和能力，在對模糊控制器4個參數的優化上，運用ASAPSO算法對其進行優化。圖5所示為ASAPSO算法對參數尋優的原理圖。

圖5 ASAPSO算法對模糊控制器的參數尋優原理圖

尋優參數為模糊控制器輸入參數量化因子ke和kec、輸出參數比例因子ku以及模糊規則權值[14]。其中ke和ku取值范圍設定為 1～10，kec和模糊規則權值取值范圍為 0～1[15]。適應度函數如下：

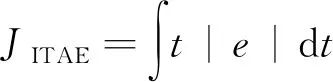
(2)

算法的流程圖如圖6所示。

4 仿真分析

4.1 仿真模型

基于MATLAB/Simulink建立的火炮隨動跟蹤系統控制模塊和執行機構仿真模型如圖7所示[16]。

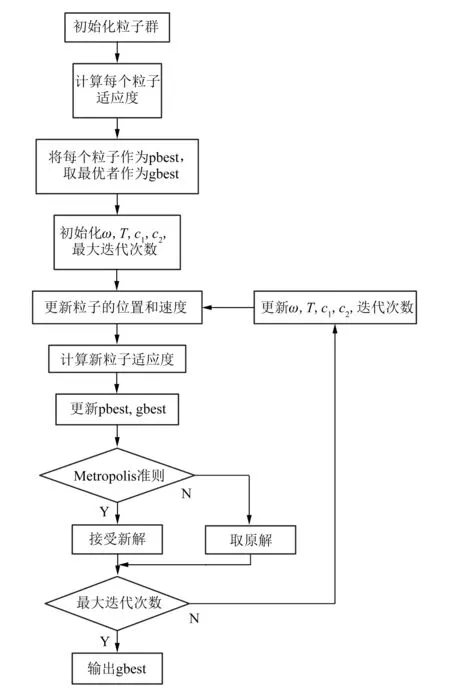
圖6 ASAPSO算法對模糊控制器的參數尋優流程圖

圖7 基于ASAPSO的火炮隨動系統模糊控制仿真模型

4.2 結果分析

PMSM的參數為：電阻R=3.8 Ω，電感L=8.7 mH，永磁磁鏈0.185 Wb,轉動慣量J=1 kg·m2，摩擦系數f=0.398 2×10-3N·m·s，負載轉矩5 N·m，極對數n=3，母線電壓值300 V。

將PD控制器加入系統位置環，設定p=6，d=0.3，設置仿真時間0.4 s，給定目標位置角度值設定為階躍信號。獲得的位置響應曲線如圖8和圖9實線所示。

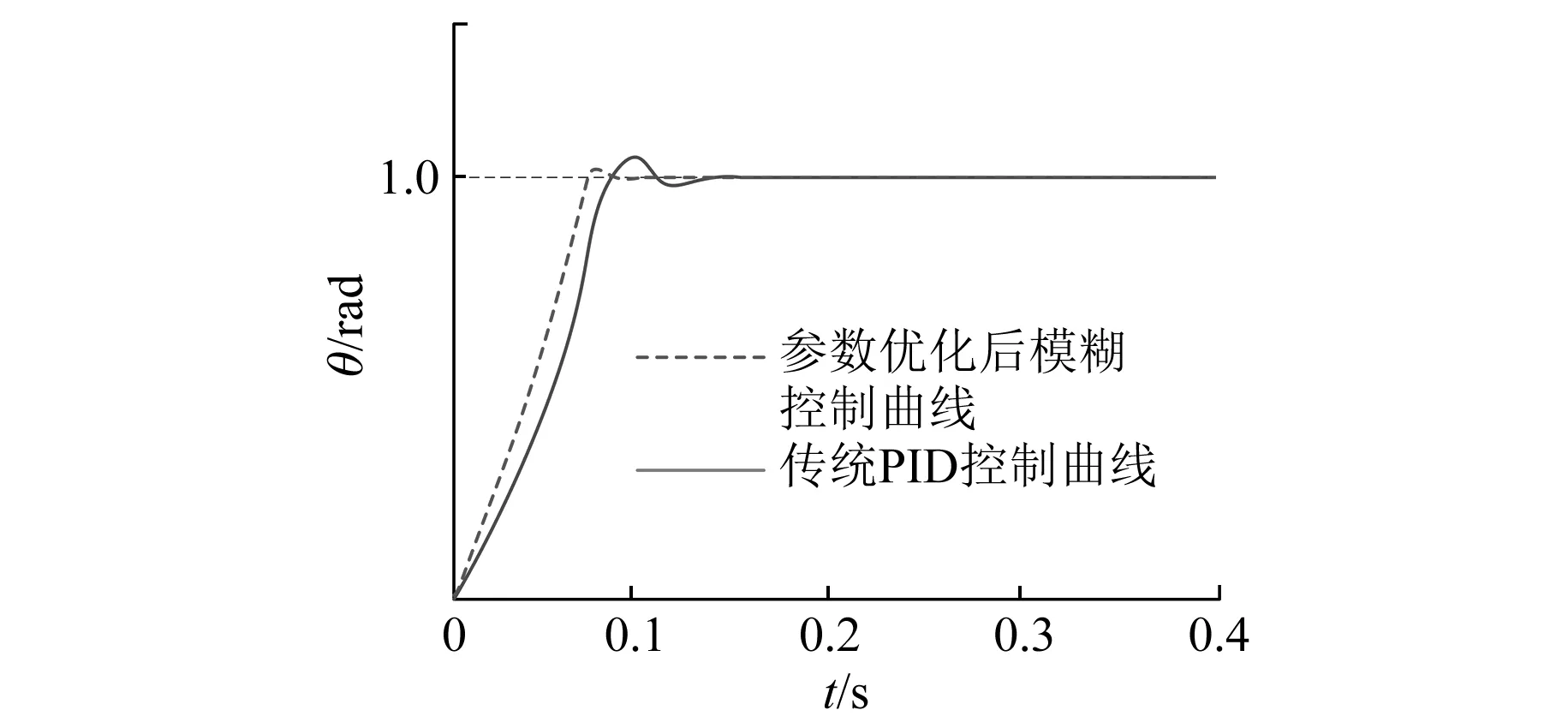
圖8 對比兩種控制器獲得的位置響應仿真波形

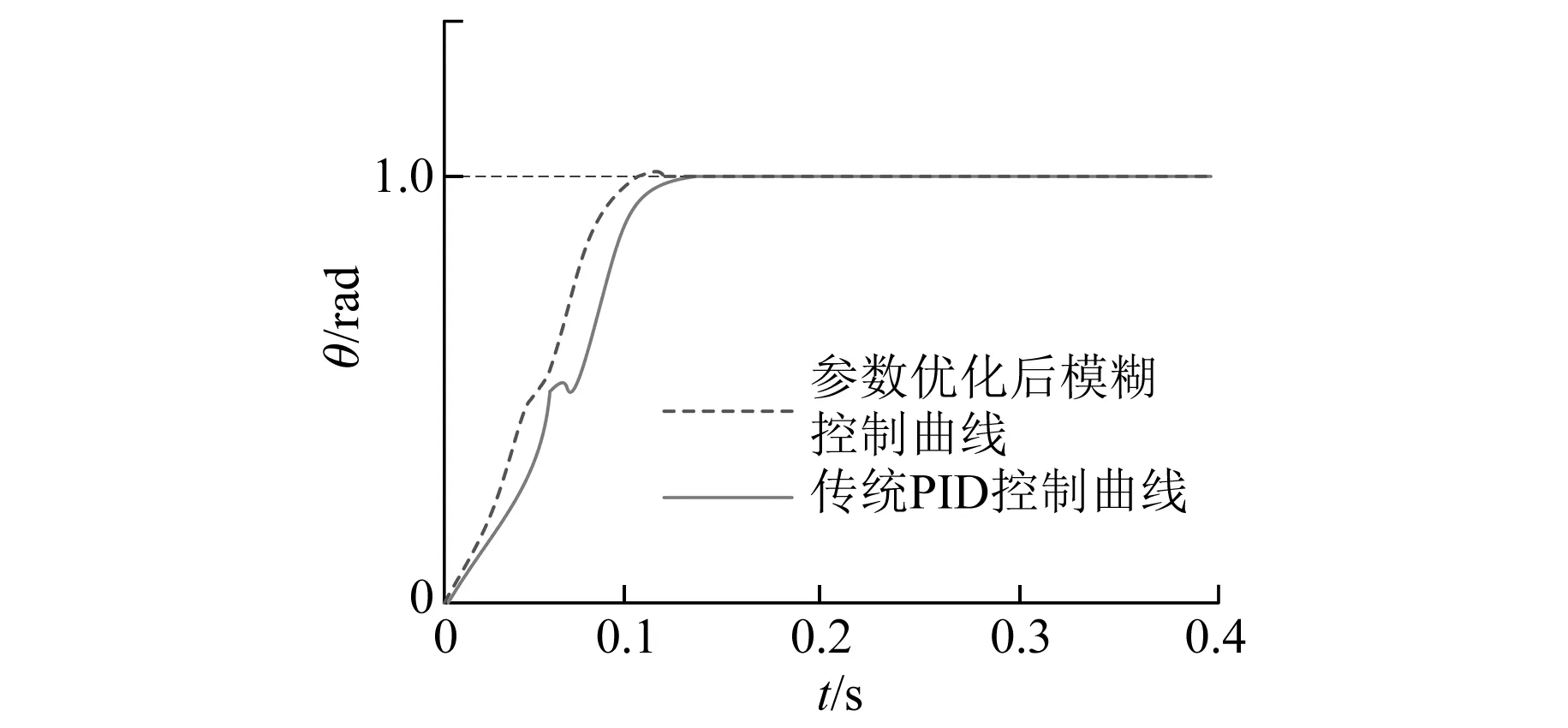
圖9 轉矩擾動對兩種控制器位置響應曲線的影響

量化比例因子分別為ke=5.08，kec=0.12，ku=4.83。將數據代入模糊控制器，替代PD控制器，用圖7所示的仿真框圖進行仿真試驗，仿真結果如圖8和圖9虛線所示。

圖8所示為傳統PID控制器和參數優化后的模糊控制器獲得的位置響應曲線。圖9所示為轉矩擾動對2種控制器位置響應曲線的影響。

圖10 參數優化后模糊控制器的跟蹤響應曲線

分析仿真結果可知：參數優化后，模糊控制器的各項性能明顯優于傳統PID控制器，當給定角度隨時間發生變化時，模糊控制器能夠更快速穩定地響應，且超調量明顯小于PID控制器。圖9顯示出了2種控制方式在轉矩擾動時的控制曲線，從圖9可以看出轉矩擾動對模糊控制器影響較小。

圖10所示為系統的跟蹤性能曲線。根據圖10的仿真曲線分析，跟蹤響應模擬目標運動最大角速度55 mrad/s，目標起始位置600 mrad，火炮身管起始位置0。通過仿真發現，參數優化后的模糊控制器能夠快速響應，具有良好的跟蹤性能。

5 結 語

本文以改進某型地面火炮隨動控制系統跟蹤性能為出發點，提出了以PMSM替代傳統直流電機作為火炮隨動系統高低和方向的執行元件，并在此基礎上研究了火炮隨動系統的位置環控制策略。通過MATLAB仿真，對比了傳統PID控制和經優化參數之后的模糊控制器作為位置控制器的響應曲線。

結果表明,自適應模擬退火粒子群優化算法的優化效果顯著，控制效果較好，系統的靜態特性和動態特性比傳統PID控制更好，能夠有效克服轉矩擾動等非線性因素的影響，系統具有較好的目標跟蹤性能。