基于SNDPSO的多峰值光伏最大功率追蹤控制研究

王 磊，朱金榮

(南京工程學院電力工程學院，江蘇南京 211100)

在實際的光伏陣列工作環境中，由于光照不均勻，往往會出現光伏陣列局部被陰影遮擋的情況。這種情況下，傳統的最大功率點追蹤(MPPT)方法已經不再適用，如電導增量法、擾動觀察法、恒定電壓法等[1-2]，開始研究局部陰影下的追蹤方法。

文獻[3]提出的算法思想是將布谷鳥算法和粒子群算法相結合，雖然一定程度上提高了尋優的精度，但所構建的數學模型比較復雜，不利于實際操作；文獻[4-6]提出的粒子群優化算法僅從權重變化的角度來改進尋優的過程，陰影情況下的改善效果存在局限性。

針對以上多峰值光伏陣列尋優算法中存在的問題，本文提出了基于迭代步長呈正態分布衰減的粒子群算法(SNDPSO)的多峰值最大功率點追蹤方法。通過在粒子的迭代過程中加入最近鄰學習的過程，將當前迭代時刻相對距離最短的粒子和全局最優粒子進行比較，提高了最優解的精度；同時讓粒子群的迭代步長呈正態分布遞減，進一步增強了粒子搜索最大功率點能力，搜索前期全局收斂能力更強，搜索后期局部收斂能力更強。

1 光伏陣列建模與特性分析

1.1 光伏電池模型分析

多個光伏電池經過串聯并聯之后就會組成光伏陣列[7-8]。光伏電池具體模型如圖1 所示。Iph表示光生電流，其大小與光伏電池板的面積和所受的光照強度成正比關系。Id表示暗電流，是指光伏電池在光照強度為零時在外電壓的作用下流過P-N 節的電流。Rs是電池內部等效的串聯電阻，通常由電池表面電阻、電極電阻所組成；Rsh表示光伏電池內部等效并聯電阻[9]。

光伏電池在太陽光照射下，產生光生伏打電動勢，進而實現了電能的輸出與傳遞，這就是光伏電池的工作機理。

由光伏電池等效電路可以得出光伏電池等效的光電流表達式：

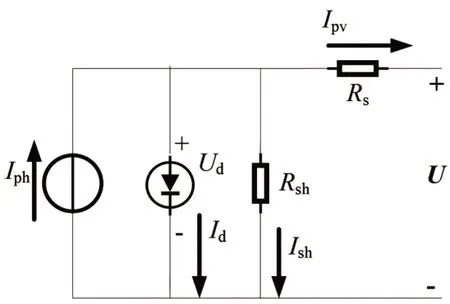
圖1 光伏電池等效電路

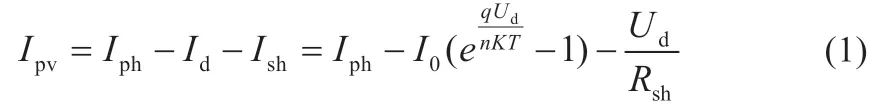
式中：I0為二極管的反向飽和電流；n為二極管的理想因子；T為光伏電池表面所受溫度；q為電子電荷大小[10]。

1.2 光伏電池P-U 特性分析

以光伏電池模型為基礎，在Matlab/Simulink 環境里對三塊光伏電池所組成的光伏陣列的P-U特性進行分析。根據光照條件設置的不同，光伏電池光照模型可以分為有陰影遮擋和無陰影遮擋，實際仿真光照測試環境為：(1)光伏陣列三塊光伏電池光照強度均為1 000 W/m2，溫度均為25 ℃，此時光伏陣列為完全光照，沒有陰影遮擋；(2)光伏陣列三塊光伏電池光照強度分別為1 000、800、600 W/m2，溫度均為25 ℃，此時光伏陣列為不完全光照，發生陰影遮擋。

兩種環境下的運行特性對比如圖2 所示，當光伏陣列內光伏板所受光照強度相同時，P-U曲線只有1 個峰值；當光伏陣列內光伏板所受光照有K種陰影遮擋情況時，P-U曲線就會有K個峰值，如果用常規的MPPT 算法追蹤最大值，就會陷入局部最優，造成追蹤失敗。

圖2 光伏陣列運行特性分析圖

2 局部陰影狀態下GMPPT 控制方法研究

2.1 基本粒子群算法

粒子群算法(PSO)是一種進化計算的算法，因為算法參數少，尋優能力強，已經被廣泛運用在非線性系統的優化問題上[9]。

粒子群算法粒子進行迭代尋優的過程中，始終利用兩個極值來不斷更新，即個體最優Pbest和全局最優Gbest，從而達到自己的最佳位置，這就是粒子群算法的工作原理。標準粒子群算法進行速度和位置更新的公式為：

式中：k表示粒子的迭代次數；w表示粒子迭代的慣性權重；c1表示自我學習因子，通常控制著粒子飛向個體極值的速度；c2表示社會學習因子，通常控制著粒子飛向全局極值的速度；r1和r2表示[0,1]之間的隨機數。

2.2 迭代步長呈正態分布遞減粒子群算法

傳統的標準粒子群算法雖然控制簡單，但由于速度更新、搜索方向、慣性權重和粒子迭代過程不能完全匹配等問題，往往最后追蹤的結果和預期有一定的偏差，有時甚至偏差較大。本文所采用的基于迭代步長呈正態分布遞減的粒子群算法能動態改變慣性權重及位置更新方式，從而加快收斂速度，提高收斂精度[9]。

2.2.1 最近鄰學習

如果在粒子群算法迭代得到當前迭代時刻的全局最優解之后，同時篩選出此時距離其它粒子平均距離最短的粒子并與全局最優解依據適應度的大小進行比較，隨后再將比較后的當前全局最優解輸出，這樣便能提高最優解的精度。

數學上有許多距離表示方式，如歐式距離、曼哈頓距離、切比雪夫距離等，本文采用曼哈頓距離來計算粒子間的距離。二維空間點a(X1,Y1,Z1…)和b(X2,Y2,Z2…)間的距離為：

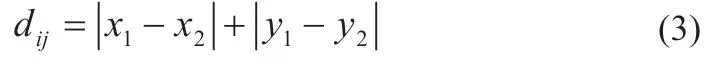
推廣到n維，可得粒子到n維平面其它點a(X1,Y1)和b(X2,Y2)等的平均曼哈頓距離為：

式中：K為算法中所含的粒子總數；n是描述粒子的維數。

t時刻全局最優值的學習按照適應度的大小來進行，假設此時的迭代次數為t，如果平均曼哈頓距離最小的粒子dmin適應度值Gdmin比當前算法得出的全局最優值Gbest的好，就采用粒子Gdmin作為當前全局最優值，否則仍采用最初得到的Gbest。t時刻全局最優解按照式(5)來更新：

2.2.2 粒子群參數改進2.2.2.1 慣性權重的改進

大量研究已經證明，較大的w能夠增強粒子的全局尋優能力，w較小則局部尋優能力增強。由此，本文采用如下余弦式的非線性變化慣性權重：

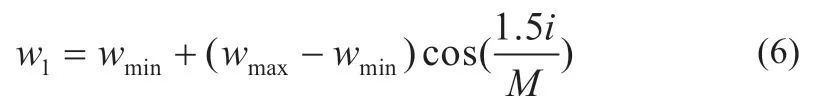
式中：wmax為最大慣性權重，本文取0.9；wmin為最小權重，本文取0.4；i為當前迭代次數；M為最大迭代次數。

圖3 為本文采用的余弦式慣性權重w1、線性遞減權重w2與指數遞減權重w3隨著迭代次數變化而變化的對比圖。w2與w3如式(7)～(8)所示：

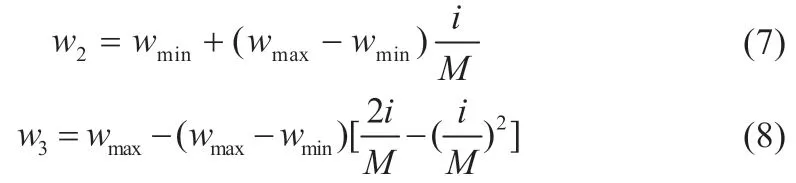
由圖3 可知，余弦遞減慣性權重在迭代初期的權重為0.9～0.85 左右，擁有充分的全局尋優能力，能夠避免陷入局部最優；算法后期，余弦遞減慣性權重為0.45～0.43 左右，擁有充分的局部尋優能力，可以進行精確的局部搜索。

圖3 不同慣性權重隨迭代次數變化曲線

2.2.2.2 迭代步長的改進

基于文獻[9]，為了使迭代步長的變化配合慣性權重的變化節奏，對粒子群算法的迭代步長進行了改進，采用迭代步長呈正態分布遞減的方式來逐步減小步長。由正態分布的特點可知，這樣的步長設置可保證算法在前期擁有較大的迭代步長，可以擴大搜索范圍而避免陷入局部最優；隨著迭代的不斷進行，步長逐漸減小，可以使搜索到的最優值更加精確。采用的位置更新公式為：

式中：λ 表示步長調整因子，隨著迭代次數的變化而變化，符合正態分布。文獻[11]中已經用實驗證明，當θ=0.443 3 時，迭代曲線能獲得最佳性能，所以θ 取值0.443 3。

3 SNDPSO 算法在多峰值MPPT中的應用

SNDPSO 算法在全局最大功率點追蹤(GMPPT)中的應用流程如圖4 所示。具體的應用過程為：首先對粒子群的基本參數進行初始化，初始化完成之后根據適應度函數計算每個粒子的適應度，將光伏陣列的輸出功率設為適應度函數；隨后結合最近鄰學習原則，獲得當前迭代次數的全局最優解，動態更新粒子的速度和位置，最后不斷迭代，滿足條件之后，結束迭代，輸出最優值。

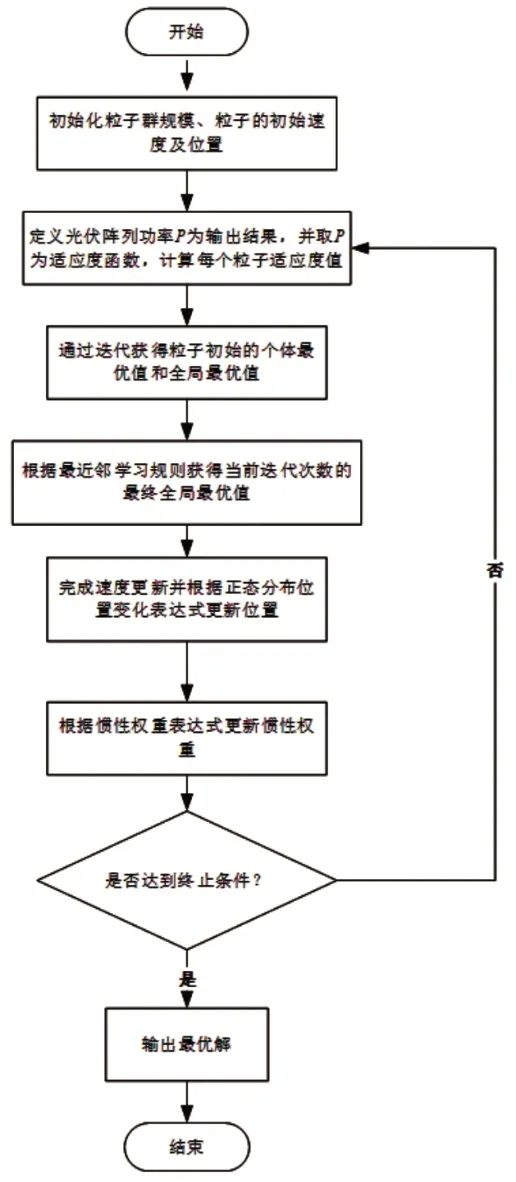
圖4 SNDPSO算法在GMPPT中的應用流程

4 仿真驗證

圖5 SNDPSO多峰值MPPT系統結構圖

SNDPSO 多峰值MPPT 系統結構圖如圖5 所示，基于SNDPSO 的多峰值GMPPT 控制電路主要由光伏電池組成的光伏陣列模塊、SNDPSO-GMPPT 模塊、Boost 阻抗變換器模塊以及負載模塊[10,12]組成。本文的光伏陣列模塊采用3 塊MSX-60 型號的光伏電池串聯而成。仿真測試所用的元件參數為：L1=1 mH，C1=800 μF，C2=300 μF，R=80 Ω。分別在完全光照、靜態陰影、動態陰影的情況下對光伏系統進行仿真。

4.1 靜態環境下的仿真測試

4.1.1 均勻光照下的仿真分析

為了保證仿真結果的精確性，將光伏陣列的三塊光伏電池溫度都設為25 ℃，三塊光伏電池的光照強度都設為1 000 W/m2。至此，均勻光照環境設置完成，此時光伏陣列理論最大輸出功率為178.1 W，均勻光照下三種算法的作用效果如圖6 所示。三種算法都能收斂并找到全局的最大功率，只是精度各有差別。SNDPSO 算法在0.021 s 收斂到了最大功率176 W，線性遞減權重算法在0.024 s 收斂到了全局的最大功率175.2 W，而基本粒子群算法的精度略有不足，在0.025 s 時收斂到了最大功率172.7 W。通過對比可以發現，SNDPSO 算法收斂到峰值的速度以及精度比線性遞減權重算法、基本粒子群算法都有提高。

4.1.2 靜態陰影下的仿真測試

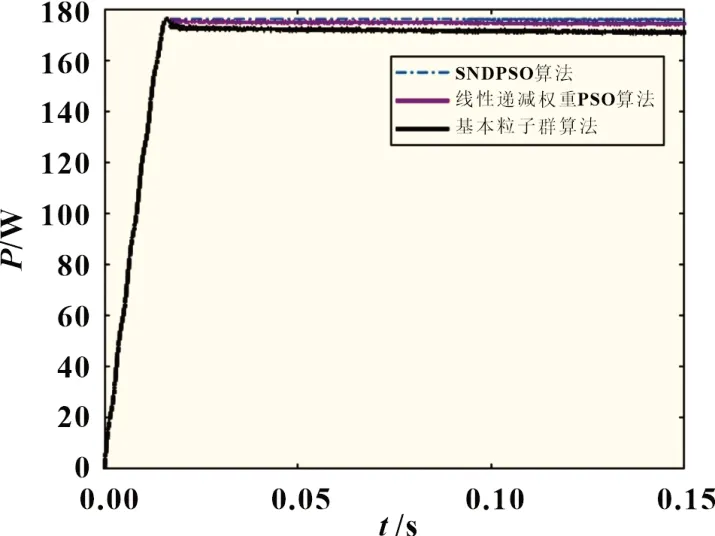
圖6 均勻光照條件下三種算法仿真效果對比圖

現將三種測試對比算法的測試參數除了光照，其它都設為相同的參數。三塊光伏板的溫度都為25 ℃，三塊光伏板的光照強度分別為1 000、800、600 W/m2，此時理論最大輸出功率為118.2 W。圖7 為SNDPSO 算法、線性遞減權重PSO 算法、基本粒子群算法在靜態陰影條件下的仿真效果對比圖。SNDPSO 算法在0.02 s 時收斂到了最大功率116.4 W，線性遞減權重粒子群算法在0.02 s 時收斂到了最大功率114 W，基本粒子群算法在0.03 s 時收斂到了最大功率104.2 W，MPPT 過程不能達到精度要求。通過對比可知，SNDPSO 算法在峰值收斂速度及精度上都有了一定程度的提升。

圖7 靜態陰影條件下三種算法仿真效果對比圖

4.2 動態環境下的仿真測試

動態環境仿真時間為0.5 s，為了模擬實際的光伏陣列所受光照的突變性以及不確定性，對光伏陣列中的三塊光伏板設置如表1 所示的光照變化。

表1 三塊光伏板動態光照強度變化情況

按照表1 中的光照強度變化對系統進行仿真，可得動態陰影條件下三種算法仿真效果，如圖8 所示。

圖8 動態陰影條件下三種算法仿真效果對比圖

按照時間順序，三個時間段的理論穩定峰值分別為135、96.77、127 W。由圖8 可知，SNDPSO 算法第一階段在0.018 s時收斂到了最大功率值133 W，在0.15 s 光照突變后僅需0.01 s 就達到了第二階段的穩定峰值95.29 W，第三階段最終的穩定峰值為125 W；線性遞減權重PSO 算法在0.02 s 達到了第一階段穩定峰值131.8 W，最終達到的峰值為122.4 W；基本粒子群算法最終達到的穩定峰值為115 W。因此，基本粒子群算法在快速陰影變化的情況下陷入了局部最優，追蹤最大值失敗。

5 結論

本文提出的算法通過在粒子迭代過程中加入最近鄰學習過程，提高了全局最優值的精度，使改進的粒子群算法能夠獲得更好的收斂值；同時引入正態分布遞減步長，動態調整步長，增強了系統的尋優能力。仿真結果表明，本文提出的算法在光伏陣列處于局部陰影的狀態下能準確、快速地收斂到最大功率點。