左半三級Sierpinski墊片上的平均捕獲時間
操 芳,吳 波
(南京財經大學 應用數學學院,南京 210023)
0 引言
近年來,復雜網絡因其在自然界中的廣泛應用而越來越受到人們的關注.在復雜網絡的研究中,一個重要的問題就是網絡的擴散效率,而平均捕獲時間就是一個很好的研究指標,它表示的是一個隨機游走者從網絡任意節點到達網絡陷阱點的平均首達時間[1-2].眾多學者對于加權三角網絡[3]、加權樹狀網絡[4]、(2,2)花網絡[5]、Koch 網絡[6]等進行研究,獲得了這些網絡上的平均捕獲時間的精確解析表達式和對應網絡上的擴散效率.上述網絡都是完整的網絡,具有全局自相似結構,但自然界中復雜網絡往往會受到攻擊造成網絡的損壞或缺失,因此,研究相關殘損網絡上的擴散效率很有意義.吳波等[7]考慮了Sierpinski墊片上的垂直切割,通過切割,得到剩余的左半網絡,研究了左半Sierpinski墊片上的平均捕獲時間并得到了該殘余網絡上的擴散效率.
本文基于Sierpinski 墊片上的切割思想,研究了三級Sierpinski 墊片上的切割,得到了左半三級Sierpinski墊片,并考慮了該殘余網絡上的平均捕獲時間.通過比較左半三級Sierpinski墊片和原始網絡上的平均捕獲時間的增長趨勢,發現它們的平均捕獲時間的增長趨勢大致一致,說明在大規模尺度下,對于三級Sierpinski墊片受到攻擊后,該殘余網絡的擴散效率基本沒有影響.
1 左半三級Sierpinski墊片的構建
左半三級Sierpinski墊片的構建:設第t代三級Sierpinski墊片為S3(t),迭代方法如下:
(1)當t = 0,S3(0)是一個等邊三角形,三個節點分別是A,B,C;
(2)當t ≥1,S3(t)由S3(t - 1)通過以下步驟產生:首先將S3(t - 1)中每個小等邊三角形三等分,然后再將等邊節點以平行于對邊的方式依次連接,并挖去中間的三個小等邊三角形.
對于第一代Sierpinski 三角形S3(1),將第一代新產生的7 個節點依次標記為D,E,F,G,H,I,J.除此之外,對于S3(t)中所有的節點,從上到下從左到右依次標上序號1,2,3,….
三級Sierpinski墊片上的切割:設第t代的一半的三級Sierpinski三角形為H3(t),H3(t)是將S3(t)由其對稱軸垂直分割,其中在對稱軸上的邊不屬于H3(t),分割后留下的左半部分即為H3(t),如圖1所示.

圖1 S3(t)與H3(t)從t = 0到t = 2連續三代的迭代圖形
對于第 t 代 S3(t),設 Nt為 S3(t)中的總節點數,Et為 S3(t)中的總邊數;對于第 t 代 H3(t),H3(t)中的總節點數,E~t為H3(t)中的總邊數.根據S3(t)的構建方法以及迭代特征,可以得出以下拓撲性質:
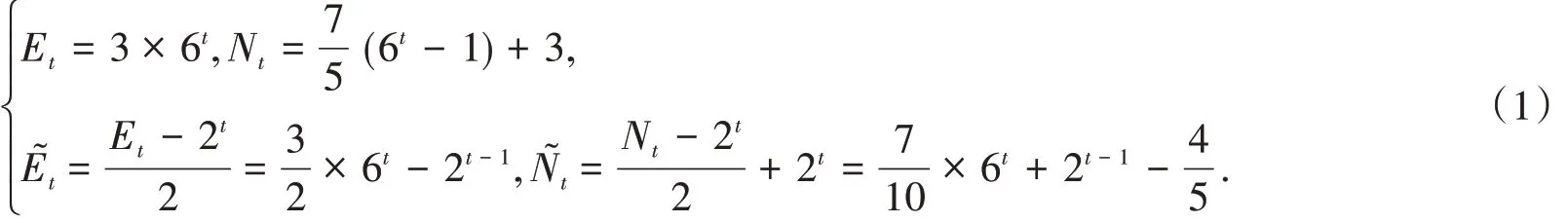
為了方便下面的計算,這里將圖1 中的A 點以及以A 點為頂點的最小三角形的三條邊去掉,所組成
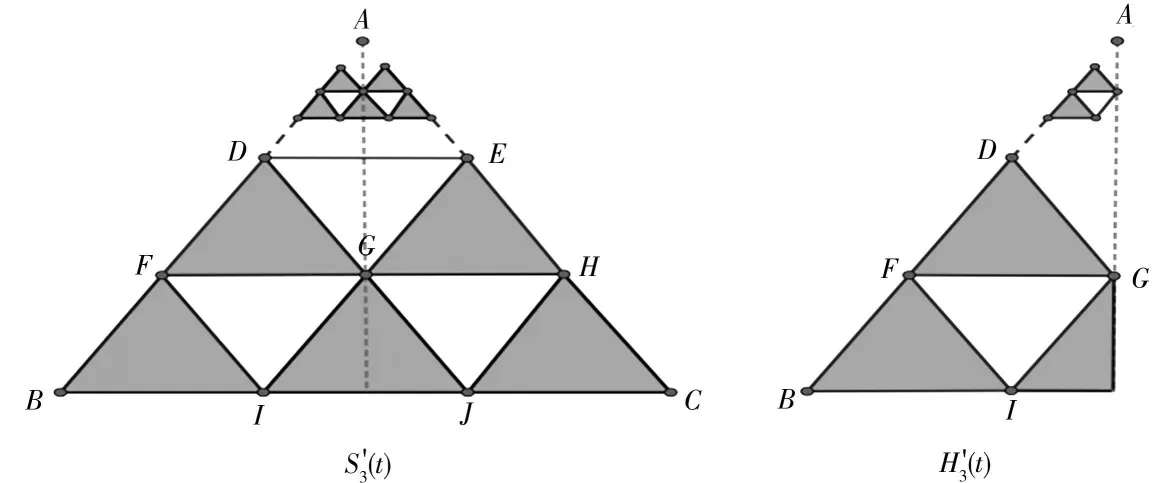
圖2 S′3(t)與H′3(t)的圖形特征

2 平均捕獲時間的解析表達式
為了研究在三級Sierpinski 墊片上的隨機無偏游走,并計算左半三級Sierpinski 墊片H3(t)上的平均捕獲時間,將給出一些定義和記號.
在圖1中,記節點A(1)為隨機無偏游走的捕獲點,Pij為隨機游走過程中節點i到節點j的概率,則

其中:di為節點i的度.
設Tij(t)和別表示節點i 到節點j 在第t 代S3(t)與H3(t)上的平均首達時間,也是在無偏隨機游走中游走者從節點i 到節點j 的期望時間;Ti(t)和為節點i(非捕獲點)到捕獲點的捕獲時間;別為S3(t)和H3(t)的平均捕獲時間,可分別表示為:
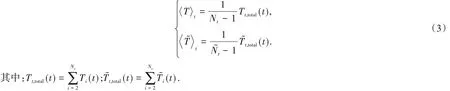
由參考文獻[8],可得
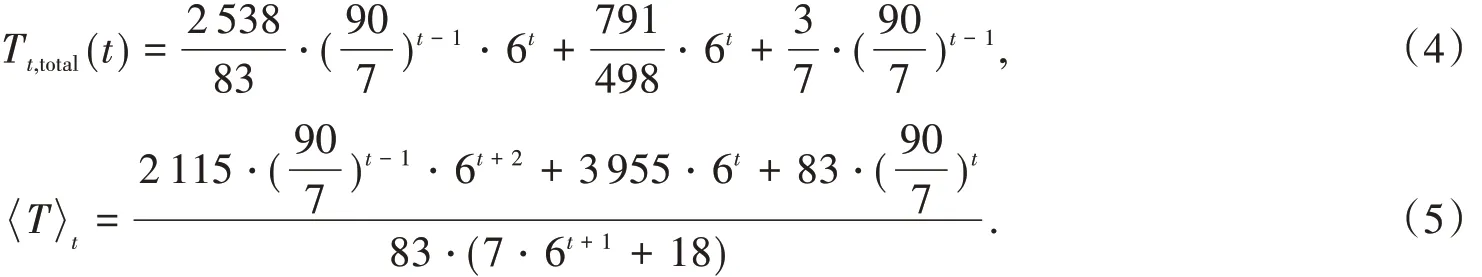
由方程組(3)可知,為了求出H3(t)上的平均捕獲時要先求


對式(7)化簡得
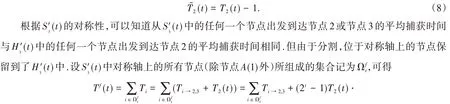
其中:Ti→2,3為S3(t)中節點i到節點2或節點3的平均首達時間.

再結合式(6)得

因此

根據三級Sierpinski墊片S3(t)的自相似性,S3(t)是由6個S3(t - 1)組成,這里將這6個三角形區域分別標記為 Γt1-1,Γt2-1,…,Γt6-1;對于每個 S3(t - 1)又是由 6 個 S3(t - 2)區域組成,可以依次標記為Γt1-2,Γt2-2,…,Γt6-2,S3(t)也是由62個Γtx-2(1 ≤ x ≤ 6)區域組成;由此可見,對于S3(t)中每個S3(y)(0 ≤ y ≤t),都是由6 個S3(y - 1)區域組成,依次標記Γy1-1,Γy2-1,…,Γy6-1,S3(t)是由6t-y個Γyx(1 ≤ x ≤ 6)組成的圖形.因此,根據這種自相似性,將S3(t)劃分為不同的區域.
此外,對于S3(t)中的三角形區域Γy1(1 ≤y ≤t),Γy1三角形上包含了節點A(1)和另外兩個節點,這里將節點A(1)記為ay,其余兩個節點分別記為by,cy,Γy1三角形內的剩下7個節點從左到右從上到下依次標記為 dy(by- 1),ey(cy- 1),fy,gy,hy,iy,jy.對于三角形區域 Γy1+1,顯然 Γy1+1包含三角形區域 Γy1,將節點A(1)記為ay+1,Γy1中的節點by,cy在Γy1+1中變為dy+1,ey+1,如圖3所示.
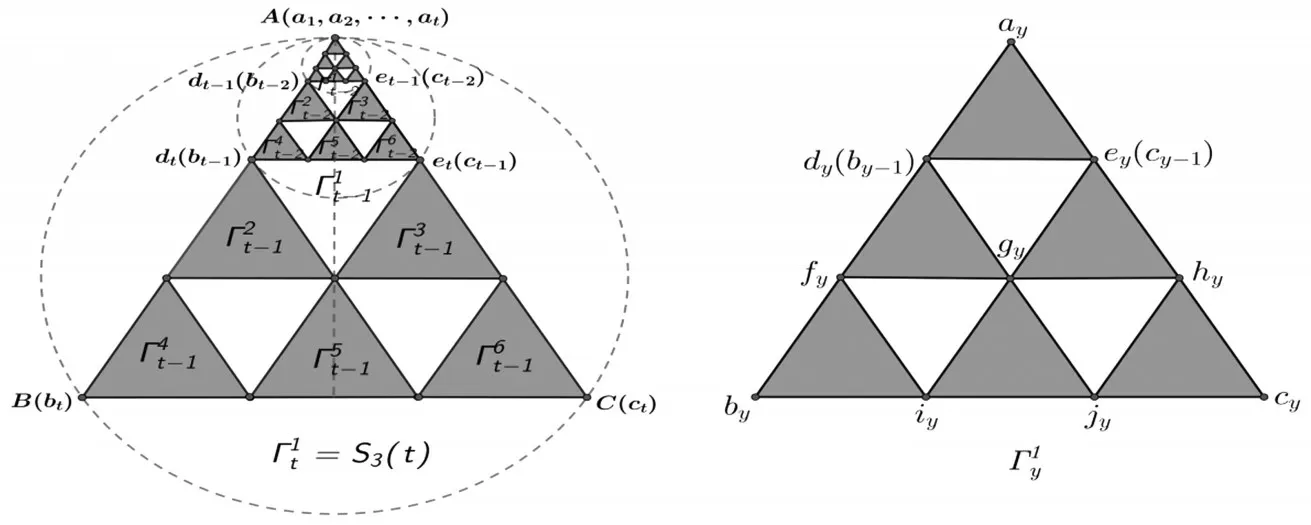
圖3 S3(t)的劃分與三角形區域Γ1y
在 S3(t)中,設 F(t)為節點 A 到節點 B 或節點 C 的平均首達時間,F′(t)為節點 A 到節點 D 或節點 E 的平均首達時間,FD,FE,FF,FG,FH,FI,FJ分別為節點D,E,F,G,H,I,J到節點B 或節點C 的平均首達時間.基于無偏Markovian隨機游走以及S3(t)網絡的自相似性,有

與第t - 1代節點A到節點B或節點C的平均首達時間相等,即

下面考慮三角形區域Γ1y(1 ≤y ≤t).設節點ay,by,cy為捕獲點,T′i(y)為節點i的平均捕獲時間,那么對于對稱軸上并在三角形區域Γ1y上的節點gy,有

由式(13)可得
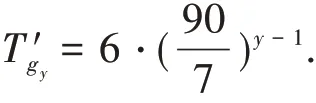
進一步,將考慮從節點gy出發,到達三個捕獲點ay,by,cy的概率,根據網絡的對稱性和自相似性,有

基于以上分析,在三級Sierpinski 墊片S3(t)網絡的無偏隨機游走過程中,從對稱軸上的節點gy出發,游走者概率經間到達捕獲節點A,分別概率到達捕獲節點B,C,且到達節點B或C的捕獲時間相等.因此,從節點gy出發到達捕獲點的捕獲時間為

代入式(17)得

由該分形無標度網絡的迭代特征,在S3(t)中觀察到對稱軸上的節點gy(t)(1 ≤y ≤t)共有(2y- 1)個節點,其中gt(t)有1個節點,gt-1(t)有2個節點,gt-2(t)有22個節點,…,g1(t)有2y-1個節點.由此可得

將式(1),(4),(19)帶入式(11)得
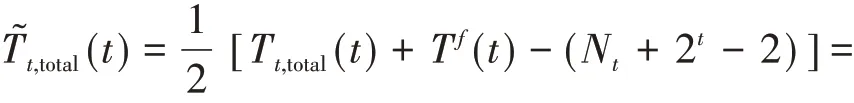
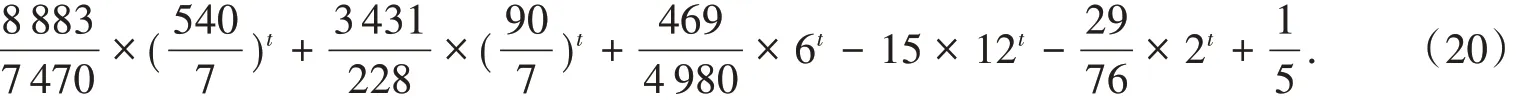
將式(20)帶入式(3)中,即可得到在H3(t)上的平均捕獲時表達式

由于


3 結論
本文主要考慮受到攻擊后的左半三級Sierpinski 墊片的分形網絡上的捕獲問題,通過分析和計算,可以得到該網絡上平均捕獲時間的解析表達式.在大規模網絡中,平均捕獲時間隨著網絡的規模的增長近似呈冪律函數增長,且冪指據本文獲得的左半三級Sierpinski 墊片H3(t)上平均捕獲時表達式以及由文獻[5]得到的原始網絡三級Sierpinski墊片S3(t)上平均捕獲時表達式進行作圖對比,如圖4所示.
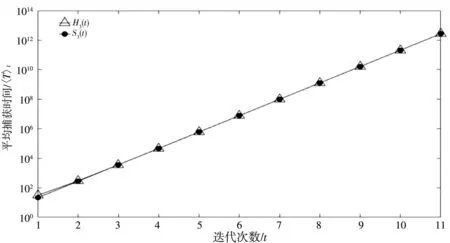
圖4 S3(t)與H3(t)上的平均捕獲時間數值模擬圖

