基于CFD的船舶形狀因子隨縮尺比及弗勞德數變化規律分析

吳思瑩，丁驚雷，陳騫

(上海外高橋造船有限公司，上海 200120)

長期以來，船模試驗被認為是實船性能評估預報最準確及可靠的方法，實船阻力預報多采用模型實驗方法，在此基礎之上線性外插得到實船阻力。外插方式主要有二因次法和三因次法[1]。二因次法也稱為弗勞德方法，其理論存在缺陷，但由于對于常規單體船型具有一定的工程應用價值且相對簡便，目前仍被廣泛應用。三因次法在理論上更為合理，也是目前各水池主要采用的方法。該換算方法引入形狀因子1+k，k為黏壓阻力與摩擦阻力比值，通過試驗或數值仿真獲得，對換算結果起關鍵性影響[2]。

三因次法中船模總阻力可表示為

Ctm=Cfm(1+k)+Cwm

(1)

式中：Ctm、Cwm分別為模型總阻力系數及興波阻力系數;Cfm為摩擦阻力系數，可由國際船模試驗水池會議(ITTC)推薦公式計算得到。

在確保弗勞德數相等的情況下，實船總阻力系數可表示為

Cts=Ctm+(Cfs-Cfm)(1+k)+ΔCf

(2)

式中，ΔCf為實船粗糙度補償系數;下標m代表模型;s代表實船。

模型各項系數可通過實驗及經驗公式得到，結合上述公式可外插得到實船阻力，作為后期船舶阻力優化、推進系統設計的重要基礎。然而計算發現通過三因次法預報的實船阻力與CFD實船模擬結果吻合度往往不夠，導致這一現象的原因十分復雜，k值的取值也是其中之一，由式(2)可知，作為公式中需外部確定的值，k值對實船阻力預報影響甚大。

確定(1+k)值的主要方法有經驗公式法、低速測試法、疊模法，以及波形測量法[3]。采用不同的方法獲得的形狀因子差異較大。ITTC針對該值及船模-實船換算方法進行過大量的研究，但迄今都未形成一個基本確定的、標準化的為各大水池所接受的取值方案及試驗規程。目前，隨著CFD技術及計算機能力的提升，已有不少學者采用CFD方法計算船模疊模并獲得準確結果，如采用CFD疊模計算確定多種類型船舶形狀因子，結果表明基于CFD疊模計算確定船舶形狀因子(1+k)準確性較高，能夠滿足工程需求[4]；基于CFD采用低速測試法計算低速時的粘壓阻力，最終獲得形狀因子。基于數值水池提出一種確定形狀因子1+k的方法，經驗證與試驗結果吻合較好[5]。可見，基于數值仿真的(1+k)值預報已在一定程度上滿足實際工程需要。然而，各水池在預報實船阻力時，不同傅汝德數下模型與實尺k值取值一般均采用同一常數。即認為不同傅汝德數模型與實尺摩擦阻力與粘性阻力比例不變，對任意工況均采用相同(1+k)值顯然是不夠準確的。為此，以某大型貨船為例，參照目前研究方法，基于PISO算法，采用VOF方法，RNG k-ε湍流模型，開展船模實船阻力實驗數值模擬。通過水池模型試驗分析船舶阻力性能，對比其變化規律并與模擬結果對比，驗證CFD計算結果的可靠性，優化計算參數，采用疊模方法不同縮尺比及弗勞德數時船舶形狀因子變化規律，為實際工程提供參考。

1 模型試驗

1.1 船舶主尺度

模型試驗在Maritime Research Institute Netherlands (MARIN)進行，試驗對象為某大型貨船，船舶主尺度見表1。

表1 主尺度參數

1.2 模型

船體模型采用木材加工而成，綜合考慮推進系統尺寸縮尺比選取為30，見圖1。

圖1 船體模型

根據相關要求，在試驗準備階段按照要求調整好船模重量、重心，以及縱向轉動慣量。模型試驗在減壓波浪水池完成，水池尺寸為240 m×18 m×8 m，試驗過程由高速攝像機拍攝，船體縱搖及升沉自由度解開，船模運動及阻力變化曲線由相關設備記錄。

1.3 試驗工況及結果

試驗主要研究該型船舶不同航速時的阻力性能，試驗結果見圖2。

圖2 船舶不同航速時的阻力性能結果

由圖2可以看出，2條曲線趨勢一致，同時摩擦阻力占比較大，達到70%以上，這主要是由于該型船舶航速較低，弗勞德數小，興波占比較小。根據式(1)可知當摩擦阻力較大時k值的變化會較大程度上影響Cwm。因此，對于這類船舶，(1+k)值的準確性會對實船阻力預報造成較大影響。

2 計算方法

基于CFD軟件Fluent計算不同航速時船模阻力性能，通過與試驗結果對比驗證計算方法準確性同時優化各類參數，在此基礎之上采用疊模方法計算不同縮尺比及弗勞德數時船舶形狀因子及其變化規律。

2.1 基礎理論

2.1.1 流體的運動控制方程

根據控制方程及給定的初始條件和邊界條件，可以求解流體中各變量值。根據連續介質假設，流體質量守恒方程(又稱為連續性方程)可表達為

式中：ρ為流體的密度；t為時間；vx、vy、vz分別為流體速度矢量在靜止坐標系沿x軸、y軸、z軸的分量。

動量守恒方程(Navier-Stokes方程)可表達為

(4)

式中：p為流體微團所受的壓力；f為3個坐標軸方向的外力分量，若只考慮重力，即僅有垂直方向的分量為g，其他方向的分量均為零。

2.1.2 VOF方法

用VOF法追蹤流場自由面時，需要在網格化的流場中定義一個稱為流體體積(volume of fluid，VOF)函數的標量函數。每個網格計算單元中的為目標流體(液體)的體積占網格容積的百分比。存在3種情況：①該單元完全被空氣充滿；②該單元完全被水充滿；③該單元部分是氣體，部分是液體，有氣液交界面。通過引入體積分數可高精度重構自由液面。

2.2 數值計算

2.2.1 模型建立

參數設置與模型試驗一致，計算模型見圖3，半模網格總數為150萬，自由液面處加密。為保證計算精度裝置周圍加密，解開模型在縱搖和升沉2個自由度的運動，在動網格設置中隨裝置同步運動。

圖3 計算域網格模型

2.2.2 計算結果

采用VOF模型，經過驗證時間步長可兼顧效率與準確性，RNGk-ε湍流模型基于PISO算法模擬不同速度下船模阻力。阻力計算結果見圖4。

圖4 模擬結果與試驗結果對比

由圖4可知，計算結果表明：數值模擬結果與試驗結果十分接近，變化規律一致，誤差均不超過10%。規律一致，準確度高，說明計算模型采用參數合理，網格大小及時間步長適中。計算方法可作為阻力計算的有效手段。

3 疊模計算

船舶1+k值可通過計算疊加模型并除以摩擦阻力來計算。疊模計算，即采用2個完全相同的模型組成一個疊加模型(水線面為對稱面)，從而避免興波阻力產生。疊合模型通常在水下或風洞中進行，測量難度較大。風洞試驗可以得到較準確的(1+k)值，但試驗結果具有一定的尺度效應；而且試驗費用較高。應用CFD技術計算疊模的粘性阻力，可節約大量時間及費用并且能夠避免試驗中的偶然誤差，從而精確控制流場，得到準確的(1+k)值。因此，考慮基于CFD的方法進行疊模仿真，計算不同縮尺比及弗勞德數時的船舶形狀因子。

3.1 模型建立

與阻力計算模型不同，疊模不需要自由液面故無需設置多相流，在水線處設置對稱面見圖5。靠近船體區域局部加密，設置邊界層，第一層厚度為0.001 5 m。總網格數為200萬。

圖5 計算域網格模型

3.2 計算結果

采用RNGk-ε湍流模型，經過驗證時間步長可兼顧效率與準確性，基于PISO算法模擬不同縮尺比及弗勞德數時船舶形狀因子及其變化規律。計算結果見圖6。

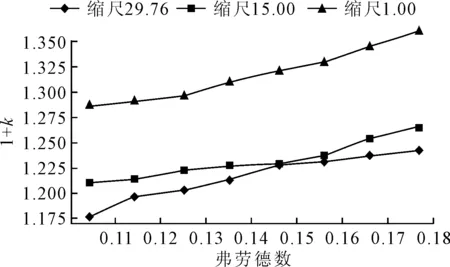
圖6 形狀因子隨縮尺比隨弗勞德數的變化

1)總體上曲線隨傅汝德數增加而增加，這是因為隨著傅汝德數增加，船舶興波與黏壓阻力占比逐漸增加，摩擦阻力相對減小，黏壓阻力與摩擦阻力比值也會略微增加。

2)不同縮尺比時k值也不一致，整體上隨縮尺比減小而增大。

在弗勞德數相同條件下對模型進行縮放時，各縮尺比模型的興波阻力系數基本不變，但這一過程中無法保證雷諾數一致，且隨著縮尺比的減小雷諾數不斷增大。根據ITTC推薦摩擦阻力公式可知，這一過程摩擦阻力系數不斷減小，占比減小。因此，推測粘壓阻力占比減小量較摩擦力要小，最終導致兩者比值呈增大趨勢。在模型尺度下，淺水區KCS的興波阻力系數顯著增大，這表明傳統的外推法必須重新考慮。總的來說，隨弗勞德數與縮尺比變化k值均會受到影響，相比較而言，船模與實船縮尺比帶來的影響更為明顯，建議實船阻力換算時重新確定k值。

4 結論

基于Fluent分析某大型油船的形狀因子及其變化規律。在驗證計算方法合理性和準確性的基礎上采用疊摸方法計算不同縮尺比及弗勞德數時船舶形狀因子，結果表明：

1)基于Fluent計算船舶阻力與模型試驗結果基本吻合，計算方法準確。

2)船舶形狀因子(1+k)隨縮尺比減小而增加。

3)船舶形狀因子(1+k)隨弗勞德數增加而增加。

4)在實船阻力換算時對于不同速度時模型與實船均采用同一k值是不合理的。建議實船阻力換算時重新計算k值。