雙曲線模型在地鐵隧道道床沉降監測中的應用

◇三亞水文地質工程地質勘察院 劉 偉

隨著城市經濟不斷發展和地面交通量的飽和，地鐵已成為現今現代化必不可少的公共交通。但是，運營期的軌道長時間使用，難免會發生軌道道床沉降，過大的沉降變形會危及到列車的行駛安全，因此進行科學的、有針對性的地鐵隧道道床的沉降監測的同時，還要建立模型進行道床沉降分析預報，提前采取預防措施。本文結合武漢某地鐵監測實例，對地鐵隧道道床沉降監測數據進行了分析研究，對變形預報的幾種常用模型，進行了簡要介紹，分析比較了其優勢與不足，分析比較了模型的適用性，結果表明雙曲線模型用于沉降預測的精度較高。

20世紀中葉以來，隨著城市化進展速度不斷的加快，各國城市人口增長迅猛，城市建設規模空前擴張。伴隨而來的便是城市地面交通量呈急劇增長的態勢，地面交通已經不堪重負，導致了城市交通堵塞，人們出行難，用車難等一系列問題。所以為了緩解地面交通問題，合理開發和利用地下空間，使其為公共交通服務成了全世界共同關注的課題。有人說:“19世紀是橋梁誕生的世紀，20世紀是高層建筑蓬勃發展的世紀，那么21世紀則是人類開發和利用地下空間的世紀”。

然而，與其他地下工程相似，地鐵隧道一般建在軟弱的第四紀沖積土層，且地質情況較為復雜，地下各類管線交錯穿插，十分密集。施工又不可避免的穿越城市相較繁華的商業中心。所以必將引起地鐵隧道道床，甚至整個地鐵隧道的縱向沉降，一定范圍內的變形沉降可視為正常情況。然而變形沉降量超過了正常情況下的變形界限，尤其是不均勻沉降。將會引起地鐵隧道道床發生沉降變形，給地鐵正常運行帶來隱患。所以為了避免由于不均勻沉降對地鐵隧道造成的巨大危害，保護隧道道床及隧道的整體結構，避免周圍建筑物受影響，必須對地鐵隧道道床進行沉降監測，對監測數據及時分析反饋，提前采取措施，防止事故發生。

1 常用的預報模型

目前常用的用于地鐵隧道道床沉降的預測方法主要有：雙曲線模型，冪多項式模型，時間序列模型和灰色模型。

1.1 雙曲線模型

在使用該模型時有一個默認的近似假設，即沉降量與時間成雙曲線關系。在作圖時將“沉降—時間”作為時間起點的時間零點，沉降曲線的關系是滿足雙曲線公式，因此時間與沉降之間的關系雙曲線表示。

兩邊取倒數得：

其中：

總的來說，雙曲線模型清晰易懂，簡單實用。可解決地鐵隧道道床的非線性沉降問題。該模型在應用于地鐵隧道道床的沉降預測方面并取得了良好的效果。并且沉降達到一定穩定程度后，模型效果更加準確。

1.2 冪多項式模型

此模型一般用在路堤沉降的預測，很少有研究人員將該模型用在地鐵隧道道床的沉降預測中，直到劉加灣[10]首次在其論文中將冪多項式用在地鐵隧道沉降預測中，并取得很好的預測效果，其原理是：地鐵隧道道床沉降量隨著時間的增大而不斷增大，但其增長速度會逐漸減小并趨于某一定值。同樣，沉降量的倒數和時間倒數也必須滿足：當時間不斷往后推移，即時間不斷增大時，時間倒數減小，那么沉降的倒數也相應的減小，那么沉降量便會增加。

利用該模型時參數得求解可以利用Excel求得，方便快捷，但是冪多項式模型只是一種純數學模型，可以用來計算，不能用來分析地鐵隧道道床沉降的機理等實際問題。

1.3 時間序列模型

通過觀測數據的整個過程我們可以發現，不管采取時間排序還是空間位置排序，這兩種方法之間都會存在不同程度的自相關關系，但是我們常用來處理該類數據的方法都假設他們之間沒有相關性，都是獨立的數據，因此從嚴格意義而言這種方法的處理方式不符合該此類項目的數據處理，所以需要新的方法來解決。此次介紹的方法是一種動態的處理方法，誕生于20世紀20年代的一種方法，經過后來的發展，廣泛用于多個領域。最大的優點在于觀測得到的數據是不連續的，但是在觀測過程中需要考慮到時間順序，通過分析前面所得的數據可以初步也測后面的結果，利用所得的數據結果進行建立數學模型，用來分析具有的相關特征。它與通常所用的回歸模型有很大的區別：主要區別在于回歸模型用來分析某一個隨機變量與其他變量之間的關系，但對于某一時間序列下所獲得的一組數據表示其之間的相關關系，此外，一般而言在實際的生產工程中的情況都是很復雜的，不能用某一條曲線或者某一個公式來展示，因此我們需要利用在這個隨機過程中所產生的數據之間的關系來表示特殊的規律。

在所有的時間序列的不同時刻的隨機變量，彼此之間有相互關系，因此這就是一種較復雜的動態數據模型。

1.4 灰色模型

我國著名學者鄧聚龍教授于20世紀80年代提出了一種新的用來解決信息不完善的分析方法，稱之為灰色模型，經過后期的發展已經得到了很廣泛的應用。一般傳統的方法認為系統產生的過程就是隨機變量產生的過程，從統計角度概率論出發，對所獲得的數據進行分析處理，但是如果對于該過程中所產生的數據較少，不具有統計的最劇本要求時，該種方法的使用就遇到了困難，需要新的方法來解決。灰色分析法將隨機過程認為是在一定范圍內變化的灰色過程，經再次此過程產生的雜亂的數據整理為一定的數列數據，在此基礎上做研究。即用有些數據是已經知道的，有些數據是不知道的樣本數據作為研究對象，通過對這些“小樣本”數據進行開發研究，提取有用的信息的過程。雖然灰色理論產生的數據是雜亂無章的，但具有整體功能，因此灰數的產生就是尋找規律。

Gm（1，1）灰色模型是灰色系統理論里的基本模型，其原理是將一些隨機上下波動的離散數據序列進行累加生成有規律的數據序列，然后進行建模預測。地鐵沉降監測的數據通常都是非等時距的時間序列，因此在建立灰色模型前，首先要對沉降數據進行處理，將其轉化為等時距數據序列。

2 工程實例

結合武漢某地鐵四期的道床實測數據，利用經典曲線方法構建地鐵隧道道床沉降的雙曲線模型，從而對該隧道道床的沉降變形趨勢做預測。

（1）構建雙曲線模型：

（2）取首期觀測時間，即3月11日為時間零點，這時認為它的沉降變形量為零，為雙曲線模型的起始點（0，0）。

（3）以R1為例，計算其雙曲線模型，令：

已知第一期為時間零點，令第二期相對于第一期沉降記作2過程，第三期相對于第一期沉降記作3過程，第四期相對于第一期沉降記作4過程。則。

已知一周期為20天，則：

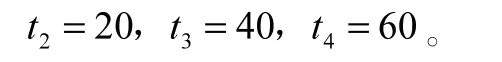
第二期相對于第一期，第三期相對于第一期，第四期相對于第一期的沉降量。所以沉降量如下：

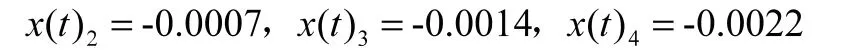
其中：

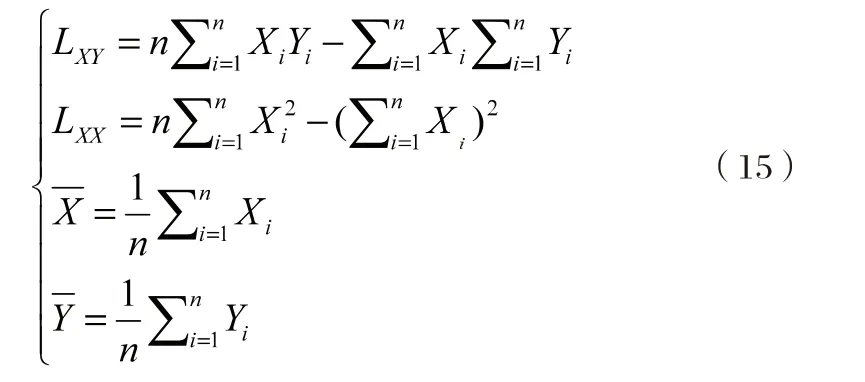
所以帶入式子可求得：

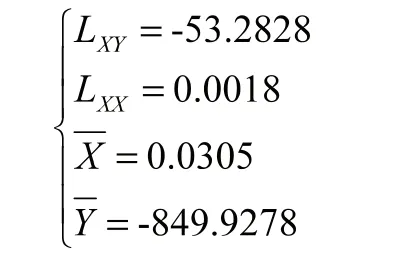
所以可求得：

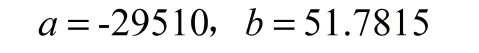
帶入式（9）得雙曲線模型：

所以計算到這就可以得出R1的雙曲線沉降預報模型，將任意時刻的帶入，便可得知該時刻的R1的道床沉降量。

按照此方法，可以將所有監測點的沉降預測模型求出來如下：

表1 各點的沉降預測曲線

驗證模型是否正確：

現已知第五期的實際觀測高程，如表2第五列所示。令第五期觀測距第一期觀測間隔為，則易知。帶入求得的雙曲線模型，可得以下結果：

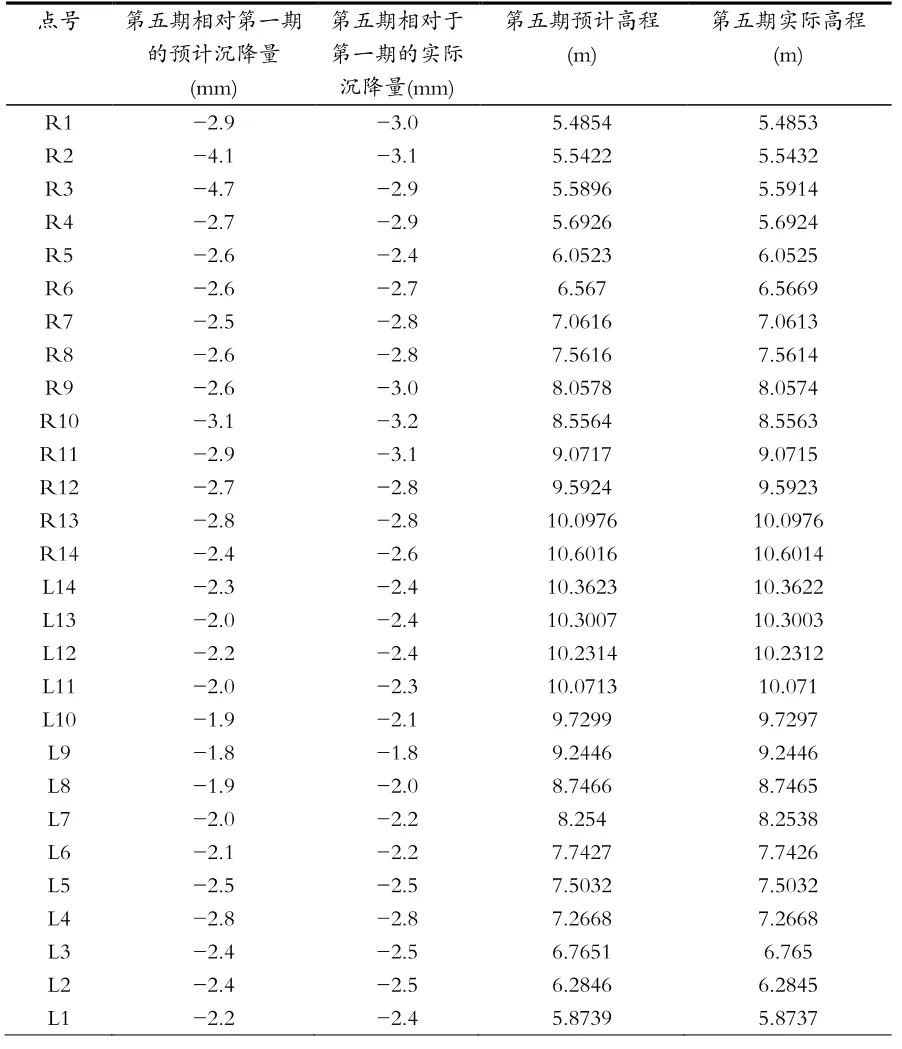
表2 各點的預計和實測高程以及預計和實際沉降量結果

其中，第五期實際高程表示實際觀測結果，第五期預計高程表示通過雙曲線預報模型求得的理論高程，第五期相對于第一期預計沉降量表示表示通過雙曲線預報模型計算出來的第五期相對于第一期的理論沉降量,第五期相對于第一期的實際沉降量為第五期高程與第一期高程之間的差值。

通過計算，我們可以把所有點的沉降趨勢用雙曲線模型表示出來，并繪制第五期相對于第一期的預計和實際沉降量對比如圖1所示。

圖1 第五期相對于第一期的預計和實際沉降量對比圖

可以看出，除了R2，R3兩個點的預計沉降量和實際沉降量相差較大，大約差了1 mm～1.5 mm。剩下的監測點預計沉降累積量和實際沉降累積量大致相同。這就證明了雙曲線模型用在地鐵隧道道床沉降預測具有可行性。

3 結語

雙曲線沉降預測計算方法是以現場實測沉降數據為基礎，并結合沉降隨時間的變化曲線、沉降量的變化趨勢情況，對地鐵隧道道床的最終沉降進行預測，預測效果較好，計算誤差較小，能夠較為準確的預測地鐵隧道道床沉降量。在上述計算過程中，基本上沒有涉及到土體的各項物理和力學性質參數，能夠適用于各種工程地質條件，計算過程簡單快捷，廣泛應用于實際工程的最終沉降預測。