基于耗散性理論的汽車底盤集成非線性魯棒約束優化控制

張家旭 趙 健 施正堂 楊 雄

1.吉林大學汽車仿真與控制國家重點實驗室，長春，1300222.中國第一汽車集團有限公司智能網聯研發院，長春，1300113.浙江亞太機電股份有限公司智能汽車控制系統研究院，杭州，311200

0 引言

目前，自動駕駛電動汽車已經成為國內外汽車產業的主要發展目標之一，而主動前輪轉向(active front steering, AFS)子系統和直接橫擺力矩控制(direct yaw-moment control, DYC)子系統是保證自動駕駛電動汽車在自動緊急轉向等極限工況下安全、穩定行駛的關鍵部件，但二者在自動緊急轉向等極限工況下呈現出強耦合特性，簡單組合的集成控制方式難以解決二者的強耦合特性對系統穩定性和控制性能的影響[1]，因此深入研究二者在自動緊急轉向等極限工況下的集成控制問題是一項具有實際意義的工作。

AFS子系統和DYC子系統的集成控制方法按照控制模型類型可劃分為線性集成控制方法、非線性集成控制方法和智能集成控制方法。線性集成方法多采用線性二自由度汽車模型作為控制模型，并基于線性魯棒控制方法設計AFS和DYC的集成控制器。例如：文獻[2]將輪胎等效側偏剛度作為線性二自由度汽車模型的不確定參數，并采用最優保性能控制方法設計AFS和DYC的集成控制器。文獻[3]將線性二自由度汽車模型轉化成線性分式變換結構控制模型，并采用魯棒H∞狀態反饋控制方法實現AFS和DYC的集成控制。文獻[4]基于左互質分解線性二自由度汽車模型建立變結構內模魯棒控制模型，并通過優化Youla參數化公式中的自由參數矩陣實現AFS和DYC的魯棒集成控制。文獻[5]以線性二自由度汽車模型的傳遞函數為基礎，采用特征軌跡方法計算AFS和DYC的控制輸入量，進而實現AFS和DYC的集成控制。在汽車自動緊急轉向等極限工況下，線性二自由度汽車模型無法準確表征汽車實際的強耦合動力學特性，使得線性集成控制方法具有較大保守性。

非線性集成控制方法和智能集成控制方法對汽車自動緊急轉向等極限工況下呈現出的強耦合特性具有更低的保守性。例如：文獻[6]采用滑模控制方法計算校正汽車橫擺角速度偏差和限制汽車質心側偏角相軌跡運動區域所需的廣義橫擺力矩，并基于輪胎逆模型將廣義橫擺力矩轉化為AFS和DYC的控制輸入，實現AFS和DYC的集成控制。文獻[7]采用非奇異快速終端滑模控制方法分別計算AFS的前輪轉角控制量和DYC的橫擺力矩控制量，并基于汽車質心側偏角相軌跡穩定區域加權AFS的前輪轉角控制量和DYC的橫擺力矩控制量，實現AFS和DYC的協調控制。文獻[8]將四輪車輛動力學模型作為控制模型，并采用非線性模型預測控制方法設計AFS和DYC的集成控制器，提高了汽車的操縱穩定性。文獻[9]基于七自由度汽車動力學模型將AFS和DYC的集成控制問題轉化成非線性最優控制問題，并通過Riccati方程求解該非線性最優控制問題。文獻[10]將七自由度汽車動力學模型作為非線性模型預測控制方法的預測模型，設計AFS和DYC的集成控制器，最小化汽車橫擺角速度和質心側偏角跟蹤誤差，提高汽車的操縱穩定性。文獻[11]采用模糊邏輯控制方法分別計算AFS的前輪轉向角控制量和DYC的橫擺力矩控制量，并基于模糊積分理論計算AFS的前輪轉向角控制量和DYC的橫擺力矩控制量的權重系數，實現AFS和DYC的集成控制。文獻[12]基于多模型切換控制理論設計一系列AFS和DYC集成控制器，并采用模糊邏輯控制方法實現所設計的AFS和DYC集成控制器的平滑切換控制。雖然非線性集成控制方法和智能集成控制方法對汽車自動緊急轉向等極限工況下呈現出的強耦合特性具有更低的保守性，但采用非線性集成控制方法和智能集成控制方法設計的汽車底盤集成控制器通常包含大量的待確定設計參數，需要借助專家經驗來標定這些待確定設計參數，以實現預期的控制目標。本文基于耗散性理論設計了一種標定參數較少的非線性魯棒控制器，以實現AFS和DYC的集成控制。

1 數學模型

簡潔、高效的汽車動力學模型是汽車底盤集成控制系統設計的基礎。忽略空氣阻力和車身的縱向、垂向、俯仰和側傾運動自由度，建立包含車身側向和橫擺運動自由度的汽車底盤集成控制模型，如圖1所示。

圖1 汽車底盤集成控制模型Fig.1 Integrated vehicle chassis control model

如圖1所示，采用汽車質心側偏角β和橫擺角速度γ描述車身的側向和橫擺運動自由度，如下所示[13]：

(1)

(2)

(3)

式中，m為整車質量；Iz為汽車繞通過質心的垂直軸的轉動慣量；vx為汽車縱向速度；Fx1、Fx2、Fx3、Fx4分別為左前、右前、左后和右后輪胎縱向力；Mu為校正橫擺力矩；δf為前輪轉向角；lf、lr分別為汽車質心到前軸和后軸的距離；tf和tr分別為前輪輪距和后輪輪距的1/2；Fyf、Fyr分別為前、后輪胎側向力的均值;Fy1、Fy2、Fy3、Fy4分別為左前、右前、左后和右后輪胎側向力。

將汽車底盤集成控制模型建模誤差考慮成系統的加性不確定性，并且將汽車整車質量、汽車縱向速度等信息測量誤差考慮成系統的乘性不確定性，則式(1)可以修正為

(4)

(5)

(6)

式中，d為系統的加性不確定性,d=[d1d2]T；未知參數θ為系統的乘性不確定性；Fy、Mz分別為汽車的側向力和橫擺力矩。

2 汽車底盤集成非線性L2增益控制

本節在Backstepping設計架構下，基于非線性魯棒控制理論設計汽車底盤集成非線性L2增益控制律，抑制系統的加性不確定性對系統性能輸出的影響。同時，借助投影修正法在汽車底盤集成非線性L2增益控制律中引入系統乘性不確定性自適應律，通過實時估計和補償系統的乘性不確定性來抑制其對系統性能輸出的影響，進一步降低系統的保守性。由AFS和DYC的集成控制目標，可得系統的性能輸出為

(7)

βd=0

(8)

(9)

(10)

(11)

式中，z1、z2分別為質心側偏角偏差和橫擺角速度偏差；σ為滑模面；βd、γd分別為期望的質心側偏角和橫擺角速度；s為拉普拉斯算子；Kγ、Tγ分別為期望橫擺角速度穩態增益和響應時間；Cf、Cr分別為前后輪胎等效側偏剛度；l為汽車軸距。

考慮輪胎-地面附著條件約束，期望的橫擺角速度進一步限制為

(12)

式中，μ為輪胎-路面附著系數峰值；g為重力加速度；ζ為式(12)簡化過程產生的影響因子，本文取ζ=0.85。

在上述分析的基礎上，我們通過李雅普諾夫穩定性理論得到以下定理。

定理針對式(4)描述的系統，設計如下汽車底盤集成非線性L2增益控制律：

(13)

采用如下自適應律更新：

(14)

式中，θmin、θmax分別為乘性不確定性的下確界和上確界；Projθ(·)為投影算子。

若選取的設計參數κ1滿足

(15)

則閉環系統在加性不確定性d≠0時是有限增益L2穩定的；在加性不確定性d=0時其對應的閉環齊次系統是漸近穩定的。

證明：選擇李雅普諾夫候選函數為

(16)

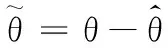
對式(16)求導，可得

(17)

將式(13)描述的汽車底盤集成非線性L2增益控制律和式(14)描述的乘性不確定性自適應律代入式(17)，可得

(18)

根據Young不等式[14]可得

(19)

(20)

將不等式(19)和不等式(20)代入式(18)，可得

(21)

(22)

對式(22)積分，可得耗散不等式

(23)

當系統的加性不確定性d=0時，對式(23)積分，可得

(24)

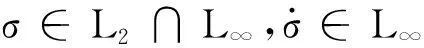
3 校正橫擺力矩約束優化分配

AFS子系統和DYC子系統分別通過調節前輪側向力和四個車輪縱向力對汽車施加校正橫擺力矩。因此，由圖1所示的汽車橫擺力矩與四個車輪輪胎力之間的關系，可得

Mu=HΔu

(25)

H=

[2lfcosδflfsinδf-tfcosδflfsinδf+tfcosδf-trtr]

(26)

Δu=[ΔFyfΔFx1ΔFx2ΔFx3ΔFx4]T

(27)

式中，H、Δu分別為控制效率矩陣和目標輪胎力增量。

目標輪胎側向力增量可以表示為

ΔFyf=-2CfΔα

(28)

式中，Δα為前輪側偏角增量。

由線性二自由度汽車動力學模型可得汽車前輪側偏角與前輪轉向角之間的幾何關系為

(29)

由于車身慣量遠大于車輪慣量，使得車輪狀態變化明顯快于車身狀態變化，因此，基于式(29)可將前輪側偏角增量表示為

Δα=-Δδf

(30)

目標輪胎縱向力增量可以表示為

ΔFxi=ΔTbi/Rwi=1,2,3,4

(31)

式中，Rw為車輪有效滾動半徑；ΔTb1、ΔTb2、ΔTb3和ΔTb4分別為左前、右前、左后和右后車輪制動力矩增量。

基于式(28)、式(29)，將式(25)修正為

Mu=H1Δu1

(32)

H1=[4Cflfcosδf(lfsinδf-tfcosδf)/Rw
(lfsinδf+tfcosδf)/Rw-tr/Rwtr/Rw]

(33)

Δu1=[ΔδfΔTb1ΔTb2ΔTb3ΔTb4]T

(34)

式中，H1為修正后的控制效率矩陣；Δu1為由目標前輪轉向角增量和目標車輪制動力矩增量組成的控制輸入。

由AFS子系統和DYC子系統的動態響應特性約束，可得

|Δδf|≤Δδfmax

(35)

|ΔTbi|≤ΔTbmaxi=1,2,3,4

(36)

式中，Δδfmax和ΔTbmax分別為前輪轉向角增量最大值和車輪制動力矩增量最大值。

為了最小化能量消耗，定義如下目標函數:

(37)

(38)

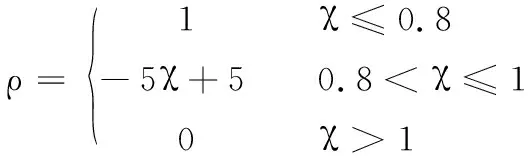
(39)

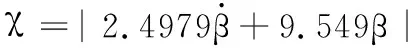
(40)

式中，W為權重矩陣；ε為修正因子，ε=10-4；Fz1、Fz2、Fz3和Fz4分別為左前、右前、左后和右后輪垂直載荷；μ1、μ2、μ3和μ4分別為左前、右前、左后和右后輪胎-路面附著系數；ρ為平滑過渡因子;χ為描述汽車穩定性的因子。

在式(37)描述的目標函數權重矩陣中引入平滑過渡因子，可以使AFS子系統主要工作在汽車質心側偏角相平面穩定區域內。同時，汽車質心側偏角相軌跡越靠近相平面穩定邊界，AFS子系統的權重越大，使得AFS子系統和DYC子系統在提升汽車操縱穩定性方面由共同主導作用平滑過渡到僅DYC子系統起主導作用。

綜上，將校正橫擺力矩約束優化問題轉化為如下的非線性規劃問題:

(41)

采用逐步二次規劃(sequential quadratic programming，SQP)法對式(41)描述的非線性規劃問題進行求解。

4 仿真結果及分析

本節采用汽車動力學仿真軟件CarSim構建模型在環測試系統，對所提出的汽車底盤集成非線性魯棒控制器的可行性和有效性進行仿真驗證。在仿真過程中，車輛參數與汽車底盤集成非線性魯棒控制器參數配置如表1所示。

表1 車輛參數與控制器參數Tab.1 The parameters of vehicle and controller

4.1 調幅正弦轉向工況

在調幅正弦轉向工況中，汽車動力學仿真軟件CarSim的路面附著系數設置為1，初始車速設置為120 km/h，前輪轉向角輸入如圖2a所示，正弦頻率設置為3.14 rad/s，調幅速率設置為0.447 °/s，未施加控制，DYC控制和集成控制的仿真對比結果如圖2b～圖2i所示。

如圖2b～圖2e所示，在系統存在加性不確定性時，未施加控制，DYC控制和集成控制的汽車均保持穩定行駛狀態，但是未施加控制的汽車無法跟隨期望橫擺角速度，呈現出不足轉向趨勢，而DYC控制和集成控制的汽車可以準確跟蹤期望橫擺角速度。如圖2f～圖2i和表2所示，相對于DYC控制的汽車，集成控制的汽車需要的車輪制動力矩更小，對汽車縱向速度的影響更小。因此，本文提出的集成控制器既可以提高汽車操縱性，又可以抑制其對汽車乘坐舒適性的影響。

(a)前輪轉向角輸入 (b)汽車橫擺角速度 (c)汽車質心側偏角

(d)汽車質心側偏角相軌跡 (e)系統加性不確定性 (f)汽車縱向速度

(g)未控制、DYC控制和集成 (h)集成控制的車輪制動力矩(i)DYC控制的車輪制動力矩 控制的前輪轉向角圖2 調幅正弦轉向工況仿真結果Fig.2 Simulation results of sine increasing amplitude sine steering

表2 調幅正弦轉向工況車輪制動力矩均值和方差Tab.2 The mean and covariance of brake torque in sine increasing amplitude steering

4.2 正弦延遲轉向工況

在正弦延遲轉向工況中，汽車動力學仿真軟件CarSim的路面附著系數設置為0.8，初始車速設置為100 km/h，前輪轉向角輸入如圖3a所示，幅值設置為5.82°，未施加控制，DYC控制和集成控制的仿真對比結果如圖3b～圖3i所示。

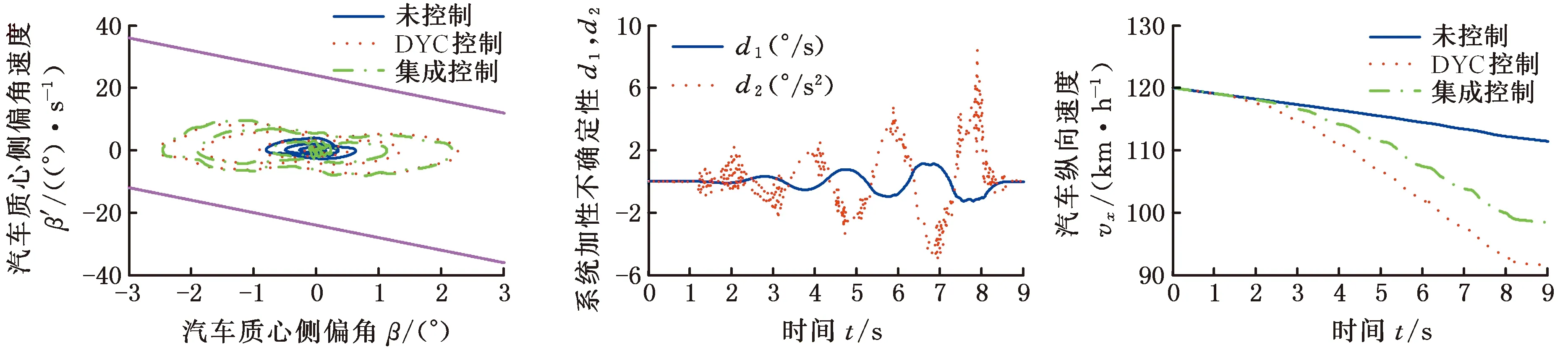
如圖3b～圖3e所示，在系統存在加性不確定性時，未施加控制的汽車在1.3s后失去穩定性，呈現出過多轉向趨勢，而DYC控制和集成控制的汽車均保持穩定行駛狀態，并且可以準確跟蹤期望橫擺角速度。同時，相對于DYC控制的汽車，集成控制的汽車對期望橫擺角速度的跟蹤精度更高。如圖3f～圖3i和表3所示，在正弦延遲轉向工況中，汽車處于極限行駛狀態，集成控制的AFS介入較少，但依然可以降低對車輪制動力矩的需求。因此，相對于DYC控制，本文提出的集成控制器既可以提高汽車操縱穩定性，又可以減小其對汽車乘坐舒適性的影響。

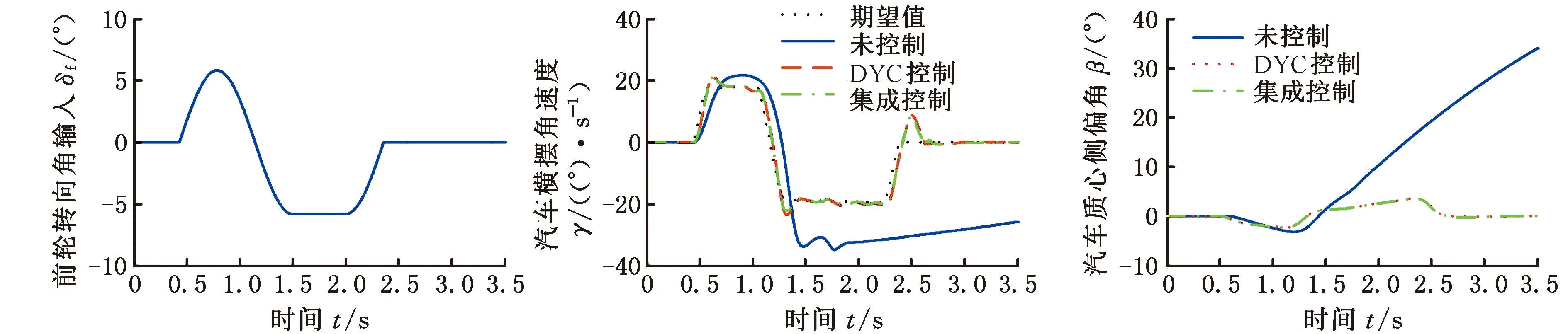
(a)前輪轉向角輸入 (b)汽車橫擺角速度 (c)汽車質心側偏角

(d)汽車質心側偏角相軌跡 (e)系統加性不確定性 (f)汽車縱向速度

(g)未控制、DYC控制和集成 (h)集成控制的車輪制動力矩(i)DYC控制的車輪制動力矩 控制的前輪轉向角圖3 正弦延遲轉向工況仿真結果Fig.3 Simulation results of sine dwell steering

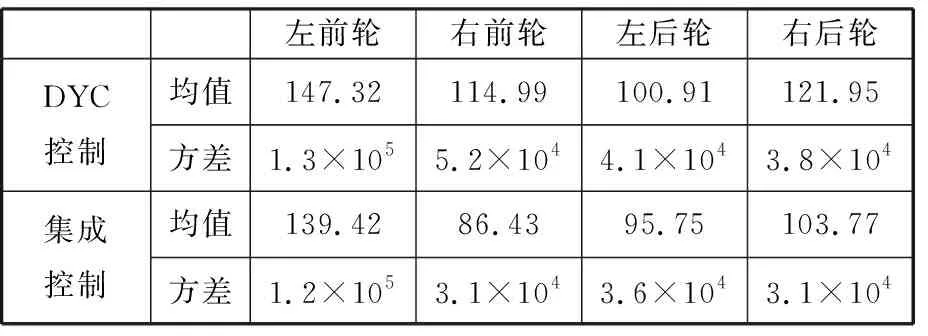
表3 正弦延遲轉向工況車輪制動力矩均值和方差Tab.3 The mean and covariance of brake torquein sine dwell steering

5 結論

(1)將汽車底盤集成控制模型建模誤差考慮成系統的加性不確定性，并且將汽車整車質量、汽車縱向速度等信息測量誤差考慮成系統的乘性不確定性，建立了包含車身側向和橫擺運動自由度的汽車底盤集成控制模型。

(2)基于耗散性理論和投影修正法設計了汽車主動前輪轉向子系統和直接橫擺力矩控制子系統集成非線性L2增益控制律，抑制系統加性不確定性和乘性不確定性對系統性能輸出的影響，并采用逐步二次規劃法來實現了所設計控制律輸出的校正橫擺力矩約束優化分配。

(3)結合車輛動力學仿真軟件對所設計的汽車底盤集成非線性魯棒控制器的可行性和有效性進行仿真驗證，結果表明：本文設計的汽車底盤集成非線性魯棒控制器對系統加性不確定性和乘性不確定性具有強魯棒性，既可以提高汽車操縱穩定性，又可以減小其對汽車乘坐舒適性的影響。

后續將搭建硬件在環試驗平臺，進一步驗證所設計的汽車底盤集成非線性魯棒控制器的可行性和有效性。