數(shù)形結(jié)合思想研究

崔亞瀾

【摘要】數(shù)形結(jié)合的思想方法在整個(gè)中學(xué)數(shù)學(xué)的知識(shí)領(lǐng)域中應(yīng)用頗為廣泛，是學(xué)習(xí)數(shù)學(xué)課程的主線(xiàn)之一，不僅可以作為一種解題方法，還可以提高學(xué)生分析問(wèn)題、解決問(wèn)題的能力.它是一種數(shù)形之間信息的轉(zhuǎn)換方法，根據(jù)具體情況，把圖形性質(zhì)問(wèn)題轉(zhuǎn)化為數(shù)量關(guān)系問(wèn)題，用代數(shù)方法分析數(shù)量關(guān)系從而解決直觀(guān)圖形問(wèn)題，或者將數(shù)量關(guān)系用圖形直觀(guān)地刻畫(huà)出來(lái).本文通過(guò)對(duì)相關(guān)的論文文獻(xiàn)進(jìn)行研究分析，歸納總結(jié)出初中、高中數(shù)學(xué)中數(shù)形結(jié)合的應(yīng)用，從數(shù)軸、韋恩圖、不等式、函數(shù)、立體幾何等多個(gè)方面進(jìn)行探究，整理數(shù)形結(jié)合思想在解題中的具體應(yīng)用.

【關(guān)鍵詞】數(shù)形結(jié)合思想;中學(xué)數(shù)學(xué);歸納總結(jié)

一、數(shù)形結(jié)合概述

（一）數(shù)形結(jié)合思想的發(fā)展由來(lái)

“數(shù)”原本只是計(jì)數(shù)的工具，而如今除了這種用途外，還可以用來(lái)表示數(shù)量;“形”在古時(shí)代表形狀，如今用來(lái)代表空間形態(tài).

在我國(guó)，“數(shù)形結(jié)合”的源頭與著名數(shù)學(xué)家華羅庚先生有著相當(dāng)大的關(guān)系.他的作品：《談?wù)勁c蜂房結(jié)構(gòu)有關(guān)的數(shù)學(xué)問(wèn)題》中的一首小詞中體現(xiàn)了該思想.

在西方，提到數(shù)形結(jié)合就要提到笛卡兒.學(xué)習(xí)了數(shù)學(xué)史的人多多少少都聽(tīng)過(guò)笛卡兒坐標(biāo)系，也就是現(xiàn)在的直角坐標(biāo)系，就是由法國(guó)人笛卡兒創(chuàng)立的.可出乎想象的是，這個(gè)巨大的發(fā)現(xiàn)是他躺在床鋪休息時(shí)得到的.他由于生病臥床不起，閑著無(wú)事就繼續(xù)思考讓他煎熬了數(shù)日的一件事.無(wú)意間的一瞥，出現(xiàn)在天花板上的小蜘蛛激起了他的思緒浪花.小蜘蛛在墻角緩緩地爬著，忙忙碌碌的，從東往西，又從南往北.那么結(jié)完網(wǎng)，它走了多少路呢？笛卡兒就試著去想怎樣才能算出蜘蛛這一路的旅程數(shù).首先他把蜘蛛當(dāng)作一圓點(diǎn)，接著反問(wèn)自己圓點(diǎn)距離墻角的距離.離墻的兩邊會(huì)有多遠(yuǎn)呢？他閉上眼睛繼續(xù)睡著，睡夢(mèng)間他似乎瞥見(jiàn)小黑點(diǎn)離兩邊墻的距離忽大忽小……他似乎悟出了些什么，睜開(kāi)眼，豁然開(kāi)朗：倘若明確圓點(diǎn)位置和兩墻間間隔，就能決定蜘蛛的位置了.明確之后，蜘蛛的位移就可順理成章地解得.于是，一個(gè)定理生成了：

彼此垂直的兩條直線(xiàn)，一個(gè)點(diǎn)可以用到這兩條直線(xiàn)的間隔，也就是用兩個(gè)數(shù)來(lái)表示，這個(gè)點(diǎn)的位置就定了下來(lái).

這個(gè)發(fā)現(xiàn)對(duì)于如今的我們來(lái)說(shuō)并不少見(jiàn)，這不就是我們非常熟悉的坐標(biāo)圖嗎？這既是數(shù)與形的聯(lián)系的首次出現(xiàn)，也是初次用數(shù)形結(jié)合的手法將代數(shù)與幾何聯(lián)系起來(lái)，打開(kāi)了解析幾何學(xué)初級(jí)階段的大門(mén).接著，就是費(fèi)馬對(duì)解析幾何的貢獻(xiàn).他用代數(shù)方法對(duì)古希臘幾何學(xué)進(jìn)行剖析，特別是對(duì)阿波羅尼奧斯圓錐曲線(xiàn)論進(jìn)行了總結(jié)和整理，對(duì)曲線(xiàn)作了一般研究.他曾提到的基本觀(guān)點(diǎn)是兩個(gè)未知量x，y確定的一個(gè)方程式，對(duì)應(yīng)著一條軌跡，可以刻畫(huà)出一條直線(xiàn)或曲線(xiàn)，就這樣，他的研究方向由方程進(jìn)化成圓錐曲線(xiàn).沿著這個(gè)思路繼續(xù)下去，在眾多數(shù)學(xué)研究者的全力探索研究下，數(shù)學(xué)的發(fā)展進(jìn)程發(fā)生了變化，解析幾何學(xué)終被創(chuàng)建出來(lái).

數(shù)形結(jié)合的思想從那時(shí)起就出現(xiàn)了，打開(kāi)了數(shù)形結(jié)合思想發(fā)展的大門(mén)，進(jìn)入了早期研究初級(jí)階段.

（二）數(shù)形結(jié)合內(nèi)涵

數(shù)與形的轉(zhuǎn)化目標(biāo)是呈現(xiàn)“形”的動(dòng)態(tài)性和直觀(guān)性，“數(shù)”的思想的科學(xué)性及嚴(yán)謹(jǐn)性，兩者互相滲透、互相影響，抓住優(yōu)點(diǎn)、因勢(shì)利導(dǎo)，從而解決問(wèn)題.

數(shù)與形不能割裂開(kāi)來(lái)，要把數(shù)或數(shù)量關(guān)系與圖形運(yùn)用一些關(guān)系連接起來(lái)，經(jīng)過(guò)對(duì)圖形的鉆研分析數(shù)量關(guān)系或用數(shù)量來(lái)升華圖形的性質(zhì).數(shù)形結(jié)合是一種典型且非平凡的數(shù)學(xué)思想方法，將抽象問(wèn)題具體化，復(fù)雜問(wèn)題簡(jiǎn)單化是它最直接、最基本的功能.數(shù)形結(jié)合是憑借數(shù)量和圖形之間的聯(lián)系來(lái)領(lǐng)會(huì)研究對(duì)象的數(shù)學(xué)特性、探求處理難點(diǎn)問(wèn)題的一種數(shù)學(xué)方式.一般情況下，在使用數(shù)形結(jié)合思想解題時(shí)，常常側(cè)重于“形”對(duì)“數(shù)”的反映，也就是要頻繁的活用圖形的簡(jiǎn)明直觀(guān)來(lái)完成對(duì)某些或某類(lèi)數(shù)學(xué)問(wèn)題的處理.所以數(shù)形結(jié)合思想可以形象地、直觀(guān)地、快捷地幫助表征問(wèn)題、理解問(wèn)題.

數(shù)形結(jié)合的根本要點(diǎn)，便是由幾何圖形的性質(zhì)來(lái)構(gòu)建數(shù)量上的聯(lián)絡(luò)網(wǎng)點(diǎn)，反過(guò)來(lái)，數(shù)量關(guān)系又制約著幾何圖形的特殊特性點(diǎn).

數(shù)形結(jié)合是數(shù)學(xué)的首要特性，萬(wàn)事萬(wàn)物皆是數(shù)形間的和諧辯證的統(tǒng)一，而非獨(dú)立對(duì)立的.故在數(shù)學(xué)學(xué)習(xí)中抓住數(shù)形結(jié)合思想就等于實(shí)實(shí)在在地握住了數(shù)學(xué)的精華和要領(lǐng)之處.

從許多對(duì)數(shù)形結(jié)合思想的深入鉆研能夠看出數(shù)形結(jié)合有很多優(yōu)點(diǎn)：可以幫助我們直觀(guān)地理解數(shù)學(xué)問(wèn)題;把問(wèn)題簡(jiǎn)潔明了地呈現(xiàn)在我們面前;有利于我們提出突破性的想法，培養(yǎng)發(fā)散思維.但世上的一切都要持辯證客觀(guān)的思想考慮，因此這個(gè)思想就有利有弊.它的缺點(diǎn)是缺乏準(zhǔn)確性和整體性，不能夠全方位的表征問(wèn)題，而且它并不能夠在數(shù)學(xué)問(wèn)題之間畫(huà)等號(hào).

數(shù)形結(jié)合的應(yīng)用概括下來(lái)大致可以分為兩種情形：

第一種是用形的生動(dòng)性和直觀(guān)性來(lái)呈現(xiàn)數(shù)之間的聯(lián)系，等于是將形作為工具，數(shù)作為需要解決的目標(biāo);第二種是通過(guò)數(shù)的準(zhǔn)確性和嚴(yán)謹(jǐn)性來(lái)表現(xiàn)形的某些特殊屬性，等于是將數(shù)作為工具，求得形的關(guān)系為目標(biāo).

本文側(cè)重探究綜合概括初中、高中數(shù)學(xué)中種種數(shù)學(xué)題型中出現(xiàn)的“數(shù)形”互相轉(zhuǎn)換的應(yīng)用.

首先來(lái)到初中，總結(jié)的是以下三個(gè)方面體現(xiàn)的數(shù)形結(jié)合.

二、初中數(shù)學(xué)中應(yīng)用的數(shù)形結(jié)合思想

（二）幾何中的數(shù)形結(jié)合

【例1】有兩棵樹(shù)，一棵高為6米，另一棵高為2米，兩樹(shù)之間間隔5米，小黃鳥(niǎo)從第一棵樹(shù)的樹(shù)梢飛到第二棵樹(shù)的樹(shù)梢，至少飛了多少米？

【分析】解決這道題就是將實(shí)際問(wèn)題轉(zhuǎn)化為數(shù)學(xué)問(wèn)題，構(gòu)建數(shù)學(xué)模型，按照題目條件畫(huà)出圖形（如圖3所示），再用勾股定理求出AB的長(zhǎng)即可.

與初中數(shù)學(xué)相比，高中數(shù)學(xué)的學(xué)習(xí)也是一樣的，對(duì)函數(shù)思想、微積分思想等需要站在數(shù)學(xué)內(nèi)部領(lǐng)域去看待數(shù)學(xué)思想，而對(duì)空間形式和數(shù)量關(guān)系結(jié)合產(chǎn)生的問(wèn)題就需要站在更感性的位置去看待.接下來(lái)，我們?cè)賮?lái)看看高中數(shù)學(xué)中數(shù)形結(jié)合思想的應(yīng)用.

三、高中階段數(shù)形結(jié)合思想的應(yīng)用

高中階段的數(shù)學(xué)知識(shí)中廣泛運(yùn)用了數(shù)形結(jié)合思想，下面筆者對(duì)一些高考數(shù)學(xué)題進(jìn)行總結(jié)歸納.

根據(jù)我國(guó)歷年來(lái)各地的數(shù)學(xué)高考試題總結(jié)發(fā)現(xiàn)，有下面幾類(lèi)數(shù)學(xué)問(wèn)題.

（一）應(yīng)用韋恩圖（Venn圖）來(lái)解決集合問(wèn)題及數(shù)軸的應(yīng)用

上題根據(jù)圖形來(lái)解決，把求陰影部分集合的問(wèn)題轉(zhuǎn)化為求兩個(gè)集合的交集問(wèn)題，將繁難的問(wèn)題簡(jiǎn)化了.

（二）數(shù)形結(jié)合思想在函數(shù)中的應(yīng)用及直角坐標(biāo)系的應(yīng)用

【例1】f（x）=x2+3x-5，x∈[t，t+1]，若f（x）的最小值記為h（t），求h（t）的表達(dá)式.

【分析】先分析函數(shù)f（x）=x2+3x-5圖像的對(duì)稱(chēng)軸與區(qū)間的位置關(guān)系，再探究函數(shù)圖像在x∈[t，t+1]上的增減狀況，接著明確在什么地方能夠取到最值，最小值具體是多少.

【解析】直接計(jì)算比較煩瑣，可利用數(shù)形結(jié)合思想來(lái)解題.觀(guān)察該式，可以發(fā)現(xiàn)這個(gè)式子的結(jié)構(gòu)和計(jì)算直線(xiàn)斜率公式的結(jié)構(gòu)相似，故把它當(dāng)成計(jì)算過(guò)點(diǎn)A（sin 20°，cos 20°）和點(diǎn)B（sin 40°，cos 40°）的直線(xiàn)斜率.如圖8所示，∵∠BOM=∠BOA=20°，且OA=OB=1，∴∠OAM=80°，∴∠OMA=60°，∴直線(xiàn)AB的傾斜角為120°，∴其斜率為tan 120°=-3，即sin 20°-sin 40°cos 20°-cos 40°=-3.

利用三角函數(shù)的本質(zhì)定義，將三角問(wèn)題放到單位圓中去解決.可以把計(jì)算三角函數(shù)值一類(lèi)的難題轉(zhuǎn)換成求直線(xiàn)斜率的問(wèn)題.

（三）依據(jù)式子的結(jié)構(gòu)，數(shù)形結(jié)合方式解決數(shù)學(xué)概念及數(shù)學(xué)表達(dá)式幾何意義的應(yīng)用

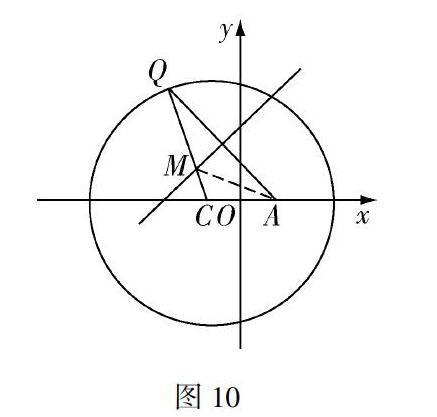
結(jié)合橢圓的定義得出點(diǎn)M的軌跡是一個(gè)橢圓，其中確定a，b，c的值是突破點(diǎn)，繼而求點(diǎn)M的軌跡方程式.另一個(gè)辦法是可以根據(jù)原有方法設(shè)點(diǎn)、找等量關(guān)系、化簡(jiǎn)來(lái)獲得軌跡方程.

四、總 結(jié)

（一）數(shù)形結(jié)合思想的意義及價(jià)值

數(shù)形結(jié)合的思想方法貫串于整個(gè)數(shù)學(xué)體系中，從兒童時(shí)期教師利用直觀(guān)的圖形及實(shí)物來(lái)教學(xué)，到中學(xué)時(shí)代中考、高考題中極為廣泛的應(yīng)用，再到大學(xué)甚至之后的數(shù)學(xué)知識(shí)學(xué)習(xí)中，都涉及此方法.它是對(duì)數(shù)學(xué)進(jìn)行研究學(xué)習(xí)的主要線(xiàn)索之一，不僅是一種解決數(shù)學(xué)題的思想方法，還是能夠讓我們深化學(xué)習(xí)、探究和研究數(shù)學(xué)的強(qiáng)有力手段、工具，能夠培養(yǎng)我們的思維能力.數(shù)形結(jié)合思想緊握“數(shù)”“形”這兩個(gè)數(shù)學(xué)中的精髓要點(diǎn)，直觀(guān)的沖擊讓我們形成對(duì)事物的感性認(rèn)知，擴(kuò)大自己的表征儲(chǔ)備，為我們內(nèi)化定義概念和性質(zhì)做鋪墊.我們對(duì)事物的了解、研究、探究大多都是由圖形作為起點(diǎn)展開(kāi)的.數(shù)和形的相互滲透連接既是數(shù)學(xué)本身發(fā)展所必需的，又是學(xué)習(xí)數(shù)學(xué)知識(shí)的需要.

對(duì)數(shù)形結(jié)合的較深的理解就是“轉(zhuǎn)化思想”，所以我們?cè)谑褂脮r(shí)要注意：第一步，要真正弄清楚概念的實(shí)質(zhì)特性和運(yùn)算的幾何意義及曲線(xiàn)的代數(shù)個(gè)性等，并且對(duì)數(shù)學(xué)題目中給定的已知信息進(jìn)行分析深化;第二步，需要做出恰當(dāng)?shù)募俣ǎ丛O(shè)參數(shù)，用參數(shù)來(lái)聯(lián)系生成條件關(guān)系，完成數(shù)與形之間的轉(zhuǎn)換;第三步，精確的利用數(shù)形結(jié)合解決問(wèn)題.

（二）數(shù)形結(jié)合思想的新發(fā)展

本篇論文說(shuō)的是數(shù)形結(jié)合這種思想方法在數(shù)學(xué)中的應(yīng)用，這僅僅體現(xiàn)了它的冰山一角，在其他的學(xué)科中數(shù)形結(jié)合思想同樣有非常廣泛的運(yùn)用.數(shù)形結(jié)合也為推動(dòng)學(xué)生的發(fā)散思維發(fā)展鋪設(shè)了新的道路，能夠提高學(xué)生的思維水平.

【參考文獻(xiàn)】

[1]趙緒臣.學(xué)會(huì)利用圖形解題[J].中學(xué)生數(shù)學(xué)，2011（08）：23-24.

[2]吳雅平.淺談數(shù)形結(jié)合的解題思想[J].山西煤炭管理干部學(xué)院學(xué)報(bào)，2004（01）：42-43.

[3]吳國(guó)秀.數(shù)形結(jié)合在解題中的巧妙應(yīng)用[J].中學(xué)理科，2001（07）：17-18.

[4]楊艷麗.數(shù)形結(jié)合思想在初中數(shù)學(xué)教學(xué)中的滲透探究[J].教育實(shí)踐與研究，2011（05）：53-55.

[5]高建彪.高中數(shù)學(xué)解題基本方法[M].上海：上海教育出版社，2004.

[6]陸家風(fēng).數(shù)形結(jié)合巧解題[J].黃石教育學(xué)院學(xué)報(bào)，2000（02）：39-41.

[7]汪江松.高中數(shù)學(xué)解題方法與技巧[M].武漢：湖北教育出版社，2006.

[8]尚文斌，聶亞瓊.淺談數(shù)形結(jié)合思想在高中數(shù)學(xué)中的應(yīng)用[J].科教文匯，2008（12）：119-137.

[9]梁國(guó)祥.數(shù)形結(jié)合在最值中的應(yīng)用[J].黔東南民族師專(zhuān)學(xué)報(bào)，2001，19（03）：77-78.

[10]張雄.數(shù)學(xué)方法論與解題研究[M].北京：高等教育出版社，2003.

[11]任小雁.如何在小學(xué)數(shù)學(xué)教學(xué)中滲透數(shù)形結(jié)合思想[J].吉林省教育學(xué)院學(xué)報(bào)，2013（10）：75-76.

[12]吳金華.數(shù)形結(jié)合思想方法在高中數(shù)學(xué)教學(xué)與解題中的應(yīng)用分析[J].數(shù)學(xué)學(xué)習(xí)與研究，2018（23）：35.