不完美排錯下測試覆蓋相關的軟件可靠性模型

張策　呂為工　邱忠銀　高天翼　江文倩　孟凡超

摘 ? 要：準確的建模軟件可靠性并對可靠性趨勢進行有效地度量與預測，對于軟件開發(fā)至關重要，越靠近軟件測試的真實過程，所提出的不完美排錯模型就應該考慮并融入更多具體的影響因素，建立構成要素間更加精準的軟件可靠性增長模型SRGM. 考慮故障檢測、修復與引入三個子過程之間的內在聯(lián)系，建立統(tǒng)一的、柔韌的不完美排錯框架模型TCM-ID，對累積檢測、修復與引入的故障數量之間的關聯(lián)實施研究，從故障檢測率、故障修復率、故障引入率角度衡量軟件測試的整體功效. 進一步，從測試覆蓋的角度，建立測試覆蓋函數相關的可靠性模型，以便于研究其對模型的擾動影響，用以評測模型的性能. 最后，在真實的應用場景下進行驗證所提出模型的有效性與合理性，模型具有較好的擬合與預測性能，整體上優(yōu)于其他模型. 本文所提出的模型，對于選擇合適的不完美排錯下測試覆蓋相關的軟件可靠性增長模型，以及提高測試效率與軟件可靠性具有重要意義.

關鍵詞：軟件可靠性;軟件可靠性增長模型;不完美排錯;測試覆蓋;框架模型

中圖分類號：TP311 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標志碼：A

Testing Coverage Software Reliability Model under Imperfect Debugging

ZHANG Ce，L?Weigong，QIU Zhongyin，GAO Tianyi，JIANG Wenqian，MENG Fanchao

（School of Computer Science and Technology，Harbin Institute of Technology at Weihai，Weihai ?264209，China）

Abstract：Accurate modeling of software reliability and effective measurement and prediction of reliability trends are critical to software development. The closer to the real process of software testing the model gets， the more specific factors should be considered and integrated into the imperfect debugging model， and the software reliability growth model （SRGM） with more accurate factors should be built. Considering the intrinsic relationships among the three sub-processes including fault detection， repair and introduction， a unified and flexible imperfect debugging framework model TCM-ID is established to study the relationships among cumulative detection， repair and introduced faults. The overall efficiency of the software test is measured from the perspective of fault detection rate， fault repair rate and fault introduction rate. Further， from the perspective of test coverage， a reliability model TCM-ID （Testing Coverage Software Reliability Model under Imperfect Debugging） is established to discuss its perturbation effect on the model and to evaluate the performance of the model. Finally， the validity and rationality of the proposed model are verified in real application scenarios. The model has better fitting and prediction performance， and it is better than other models overall. The model proposed in this paper is of great significance for selecting the appropriate SRGM for the test coverage under the imperfect debugging conditions and improving the test efficiency and software reliability.

Key words：software reliability;software reliability growth model（SRGM）;imperfect debugging;testing coverage;framework model

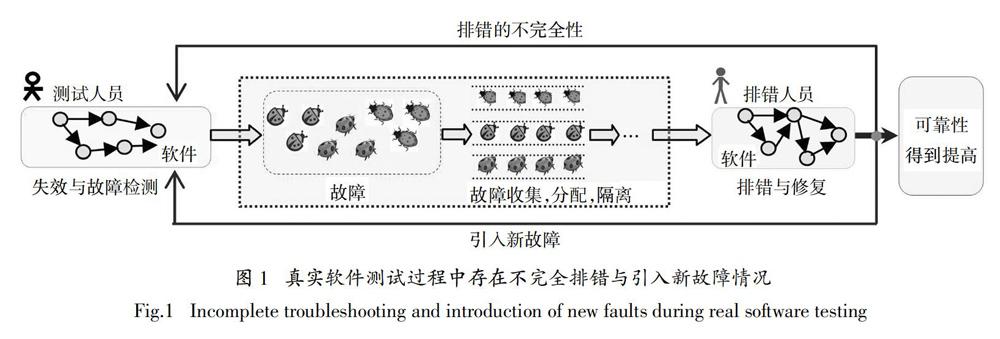
軟件測試是軟件可靠性不斷增長的過程，是提高可靠性必不可少的關鍵環(huán)節(jié). 軟件測試過程是軟件測試人員在某種測試環(huán)境下，按照預定的測試策略或計劃，執(zhí)行測試案例，發(fā)現與檢測軟件運行過程中的失效，定位、收集和記錄故障，并進行故障修復的過程. 整個過程大致由三個部分組成，即故障檢測過程FDP（Fault Detection Process）、故障分析過程FAP（Fault Analysis Process）和故障修復過程FCP（Fault Correction Process）[1]. 圖1描述了軟件測試與排錯過程，可以看出，隨著故障被不斷的檢測和修復，軟件的可靠性得到持續(xù)提高.

由于軟件測試與排錯的復雜性、隨機性和不確定性[2-5]，檢測到的故障在修復階段可能沒有成功排除，出現排錯的不完全現象，如圖1中上面的反饋線;另外，在故障的修復過程中，由于程序的內在結構邏輯可能被破壞，從而存在引入新故障的可能[6-7]，如圖1中下面的反饋線. 包括這兩種情況等實際測試情況在內的復合現象通常被稱為不完美排錯現象. 因此，不完美排錯[5，8-12]是更加靠近真實軟件測試過程的研究，能夠描述更多的實際情形，得到了科研人員的重視. 軟件可靠性增長模型SRGM（Software Reliability and Growth Model）[13-15]可用來對軟件測試過程進行建模，通過數學手段來定量描述故障檢測、修復等關系，是對軟件可靠性進行有效度量與預測的重要工具. 在現有SRGM研究看來，不完美排錯是對實際軟件測試過程的一種近似抽象，包括排錯的不徹底現象[16]、引入新故障現象[9-10]或者是軟件中總故障數量a（t）的不斷增長現象[17]. 這些研究從不同角度和內容對測試過程進行了不完美排錯建模，有力地推動了SRGM的發(fā)展，但對不完美排錯的全面準確描述還不夠深入. 例如，很多大型軟件的測試過程中，故障排錯的不完全與引入新故障通常是同時存在的，二者相互交織在一起. 從測試覆蓋角度來看，包括經典的G-O（Goel L - Okumoto K）模型[18-19]在內的很多完美排錯和不完美排錯模型，均默認或假定測試覆蓋滿足100%，但顯然這是不切合實際的. 測試覆蓋針對程序結構進行測試策略下的測試，涵蓋語句覆蓋、分支覆蓋、條件覆蓋、路徑覆蓋、數據流覆蓋、函數覆蓋、調用覆蓋，因此從測試覆蓋的角度研究可靠性可以更加細膩地剖析可靠性的變動. 事實上，軟件測試過程是較為復雜的隨機過程. 為了得到更加有效的可靠性模型，就需要對測試過程中的隨機因素加以考慮.

本文在現有研究的基礎上提出一種全面考慮不完美排錯的軟件可靠性過程分析方法，明確考慮到了測試覆蓋，所提出的模型能夠更加準確地描述軟件測試過程.

文章結構安排如下：第1節(jié)對考慮真實測試過程的不完美排錯進行建模，提出了一種不完美排錯下測試覆蓋相關的軟件可靠性增長框架模型，進而給出了具體的測試覆蓋函數相關的可靠性模型;第2節(jié)通過公開發(fā)表的失效數據集驗證了所提出模型的有效性與合理性. 最后總結了全文，并指出后續(xù)研究方向.

1 ? 不完美排錯下測試覆蓋相關的軟件可靠性

增長框架模型

1.1 ? 基本假設

基于對測試環(huán)境的認知，遵循SRGM研究所作假設的常規(guī)共識，考慮測試覆蓋下的不完美排錯模型假設如下[18，20-24]：

1）軟件失效隨機發(fā)生，故障檢測與修復過程服從非齊次泊松過程NHPP（Non-Homogeneous Poisson Process）[12，18，25]，即到t時刻累積檢測出的故障數N（t）服從期望函數為m（t）的NHPP分布，滿足m（t=0）=0，則利用NHPP基本性質，能夠得到t時刻檢測到k個故障的概率以及m（t）與故障檢測率λ（t）的基本關系：

Pr [N（t）=k]=，k = 0，1，2，… ? ?（1）

m（t） = λ（τ）dτ ? ? ? （2）

2）軟件失效由軟件中剩余的故障引發(fā);

3）在時間區(qū)間（t，t+Δt）內，最多發(fā)生一個故障，且所檢測到的故障數量與當前剩余的故障總數成比例;

4）在時間區(qū)間（t，t+Δt）內，被修復的故障數量與被檢測的故障數量成比例;

5）故障修復的過程中，存在引入新故障的現象，引入的故障數量與累積修復的故障數量成比例.

1.2 ? 不完美測試框架模型

令m（t）和r（t）分別表示截止至t時刻累積檢測到和修復的故障數量，a（t）表示t時刻軟件中總的故障數量. 則基于上述假設，建立了下面的基于故障檢測率函數b（t）、故障修復函數p（t）和新故障引入函數γ（t）的故障檢測、修復與引入模型，如式（3）所示.

式（3）中第一個方程基于第三條假設，描述了t時刻檢測的故障數量與剩余故障數量的關系;第二個方程基于第五條假設，從t時刻新增加的故障角度建立了總故障個數a（t）的表達式;第三個方程基于第四條假設，對Δt時間內檢測的故障數量與修復的故障數量進行建模.

b（t）是故障檢測率，表示測試人員在測試環(huán)境下運用測試技術檢測出故障的概率，其可以從多種角度來進行設定. 當考慮測試覆蓋時，故障檢測率b（t）可表示如下：

c（t）表示截止至t時刻已經被（測試案例）測試的代碼所占的百分比;1 - c（t）表示到t時刻尚未被測試的代碼所覆蓋的比例. 顯然，c（t）的導數c′（t），則表示t時刻點上的測試覆蓋率. 易知，故障檢測率FDR（Fault Detection Rate）[26]與c′（t）成正比例，且與1-c（t）成反比例，b（t） = c′（t）/[1 - c（t）]. r（t）表示新故障引入率，p（t）表示t時刻故障被成功修復的比例函數.

此微分方程組的邊界條件為：

m（0） = 0r（0） = 0a（0） = a ? ? ? ? （5）

這里，采用如下過程進行求解，為方便令：

至此，完成了測試覆蓋函數下考慮故障不完全修復與新故障引入的不完美測試框架模型的構建，得到了SRGM研究中重要的關鍵內容：m（t）、r（t）和a（t）. 從測試過程的整體來看，截止t時刻，累積修復的故障數量r（t）小于等于累積檢測的故障數量m（t），m（t）小于軟件中故障總數. 將上述模型簡記為TCM-ID（Testing Coverage Software Reliability Model under Imperfect Debugging）.

測試階段的軟件可靠性表示為R（x|T），即假定軟件上一次失效時間是T （T≥0，x>0），依據NHPP基本性質，可得在（T，T+x）內的軟件可靠性表示為：

若假定從T=0開始，則m（t）=0，將式（15）代入式（19），則可以得到更易理解的可靠性R（x），如式（20）所示：

1.3 ? 關于模型的柔韌型討論

TCM-ID采用微分方程組的形式對不完美排錯下的測試過程進行建模，其中融入了故障排錯率p（t）、故障檢測率b（t）和新故障引入率λ（t），因此求解得到的m（t）、r（t）和a（t）是多參數的融合體. 為此，可以看出該模型是具有較強柔韌性的框架模型，可以支持一系列的不完美排錯相關的具體模型的構建.

1）采用方程組的形式建立了不完美排錯相關的軟件可靠性模型;

2）關鍵的故障數量表達式（m（t）、c（t）和a（t））均是通過求解得出，且具體由3個參變量函數來決定，即故障檢測率b（t）、故障排錯概率p（t）以及故障引入率λ（t），這些參變量函數可根據實際情況進行設定，這為模型的框架性、統(tǒng)一性和柔韌性提供了支撐，為SRGM所關注的m（t）等信息提供了更為客觀的依據，從而使其更加直接地受制于實際因素;

3）故障修復過程中存在故障的引入，因此，單位時間內新增加的故障數量應與累積修復的故障數量成比例.

1.4 ? 測試覆蓋函數視角下TCM-ID

故障檢測率FDR：b（t）是可靠性建模中必不可少的構成元素，其描述了測試環(huán)境下故障被檢測出來的能力. 當前研究中以人為設定FDR為某種函數為主，且為求解簡便，多以b（t）=b為常見. 顯然，由于測試環(huán)境的復雜性，測試階段、測試策略等因素的不同會使FDR呈現多種變化形式. 文獻[27-28]認為測試覆蓋函數與FDR緊密相關，可以成為FDR建模的元素，并提出c′（t）/（1-c（t））可用來度量t時刻的故障檢測率b（t）. c′（t）描述了測試用例[29]的執(zhí)行情況，通過c（t）的變動可以獲得不同的FDR函數. 這樣，可以得到下述的不完美排錯過程模型：

依據上述求解過程進行求解，可以得到測試覆蓋函數下的不完美測試模型中的m（t）：

至此，從測試覆蓋函數c（t）的角度得到了SRGM研究中的關鍵待求變量m（t）. 通過設定各類測試覆蓋函數c（t），可以得到一系列相關的m（t）. 為簡化計算，不妨令p（t） = p，γ（t） = γ. 這里令a（t） = （1 - e-btc）[30]，則可求得m（t）如下：

可以看出，本文所提出的模型在測試覆蓋函數視角下，將可靠性研究由傳統(tǒng)的FDR相關演進為不完美排錯下測試覆蓋相關的可靠性模型.

2 ? 數值算例

2.1 ? 參與比較的模型

這里選定了一系列典型的不完美排錯模型參與比較，以對比模型之間的性能差異，如表1所示.

選取4個已被廣泛用來進行驗證可靠性模型性能的失效數據集DS1[24]，DS2[35]，DS3[36]，DS4[22]，它們均來自國際知名公司在系統(tǒng)開發(fā)過程中所搜集的軟件測試失效數據，具有廣泛的代表性，可以表征多樣的軟件測試場景;同時，選取通過可靠性過程仿真獲得的失效數據集DS5[37]進行同步驗證，該數據集來自基于率函數對不完美排錯下的軟件測試情況進行仿真，更加靠近真實情況.

2.2 ? 比較標準

采用均方誤差值（Mean Square Error，MSE），Variation，RMS-PE和回歸曲線方程的相關指數（R-square）度量曲線擬合效果，利用相對誤差（Relative Error，RE）度量模型的預測能力.

式中：yi表示到ti時累積的失效個數，m（ti）表示到ti時利用模型得到的估算值，k表示失效數據樣本數量. 顯然，MSE，Variance，RMS-PE和BMMRE的值越小，R-square值越接近于1，擬合效果越好;RE越趨近于0，模型預測效果越好.

2.3 ? 性能驗證

為了驗證所提出模型的有效性，將表1中的模型在5個公開發(fā)表的真實數據集DS1～DS5上進行實驗. 基于擬合得到的參數值，計算5個失效數據中不同時刻各個模型的m（t），繪制出m（t）與真實失效數據間的擬合曲線，如圖2所示.

從圖2可以直觀看出：

1）在DS1、DS2、DS4和DS5上，個別模型已經嚴重偏離真實的失效曲線（M-1模型與DS1、DS2、DS4和DS5上的失效數據曲線走勢嚴重不符;M-3模型在DS2和DS4上也產生了同樣的情況），表明模型已經嚴重失真. 在DS3上參與比較的模型，在整體趨勢上與真實的失效數據相一致;

2）在DS5上，本文所提出的模型同樣表現出優(yōu)秀性能，與失效數據曲線走勢保持一致，重疊度高;

3）在所有5個數據集上，本文提出的模型TCM-ID與真實的失效數據曲線有較高程度的重合，這表明該模型具有較好的擬合性能.

為了進一步區(qū)分不同模型的性能差異，這里定量化地計算并列出了各模型在5個擬合標準上的數值，如表2所示.

從表2可以直觀看到，與圖2曲線相一致，個別模型的擬合指標數值不理想，反映出其性能較差（M-1模型在DS1、DS2和DS4上性能欠佳;M-3模型在DS2和DS4上也有同樣的情況）. 在DS2數據集上，本文所提出的模型在4個指標上均優(yōu)于其他模型（MSE，Variance，RMS-PE，BMMRE數值越小表明模型性能越好：R-square越接近于1表明模型性能越好），并在數值上具有明顯的比較優(yōu)勢，顯示出了該模型優(yōu)異的性能. 在DS3上，所提出的模型TCM-ID在前4個指標上同樣表現出了優(yōu)秀的性能;在BMMRE指標上與其他模型處于相同量級，沒有出現明顯的差異，綜合來看，可以表明模型TCM-ID具有優(yōu)秀的性能. 在DS4上，M-5和本文所提出的模型均表現出了優(yōu)異的性能，二者在數值上較為接近，處于同一數量級別（M-5在MSE，Variance，RMS-PE這3個指標上略優(yōu)于TCM-ID，TCM-ID在R-square和BMMRE上優(yōu)于M-5），顯示出了TCM-ID的良好性能;綜合全部數據集來看，M-5僅僅在DS4上表現優(yōu)秀，表明該模型具有很強的不穩(wěn)定性能，難以適應更多的數據集. 因此TCM-ID的性能要明顯優(yōu)于M-5. 同樣，M-4也僅僅在DS1上顯示出了優(yōu)秀的性能，同樣具有較強的隨機性，不如本文所提出的模型具有在多個數據集上連續(xù)優(yōu)秀的穩(wěn)定性. 在仿真失效數據集DS5上，TCM-ID在5個具體的指標上均優(yōu)于其他7個模型，同樣顯示出了優(yōu)秀的性能. DS5來自于對不完美排錯軟件測試過程的仿真，這與本文建立的不完美測試框架模型具有一致性，對更加靠近真實故障檢測、修復與引入的實際情況進行了準確描述.

綜上可以看出，本文所提出的模型TCM-ID能夠保持連貫的穩(wěn)定性能，在全部失效數據集上或者處于最優(yōu)或者處于良好（且與某個數據集上表現優(yōu)秀的模型之間差異較小）. 這種原因可以解釋為：

1）TCM-ID在建模中充分考慮到了排錯的不完全性與排錯過程中存在新故障引入這種真實存在的客觀現象，將更多的軟件測試過程中的隨機性納入到模型中，將不完美排錯用微分方程進行了準確的建模. 相比之下，M-4與M-5模型因缺少對真實不完美排錯因素的考慮，或者僅從不完全排錯或新故障引入某個單一方面建模，導致它們僅能在個別數據集上表現優(yōu)秀.

2）在測試覆蓋方面，本文的模型在建模過程中引入了測試覆蓋函數，用以描述和建模測試過程中故障被測試覆蓋從而被檢測出來的程度，更加精準地刻畫了真實測試的情形;相比之下，其他模型認為測試覆蓋是100%，這與真實的測試過程并不相符.

所有這些差異，使得其他模型的綜合性能劣于本文所提出的模型.

關于模型的預測性能，圖3分別繪制了不同模型在5個失效數據集上的相對誤差RE曲線. 整體上看，在失效數據集的后半程時間內，模型開始進行快速地收斂，逐漸向著0曲線靠攏，表明其預測性能在提高. 從圖3可以看出，本文所提出的模型能夠較好地向著0曲線收縮，特別是在測試時間過半之后收縮速度明顯加快.

至此，從圖2、圖3和表2可以看出，本文所提出的模型充分考慮到了軟件測試與排錯過程的不完美特點，并將測試覆蓋作為重要的影響因素進行考慮，所建立的模型具有較好的擬合與預測性能，整體上優(yōu)于其他模型.

3 ? 結論與下一步研究內容

針對測試環(huán)境的復雜性和隨機性，以及當前研究所做假設偏離實際的問題，本文建立了涵蓋故障檢測、修復和新故障引入的統(tǒng)一的不完美排錯框架模型，模型中融入了測試覆蓋因素，使得測試中的實施細節(jié)得以在數學模型中呈現，進而從測試覆蓋的角度研究分類模式下測試覆蓋的能力，對可靠性性能影響評測進行了深入研究. 因考慮到更多真實測試的隨機性，本文所建立的模型不僅具有良好的柔韌性，在擬合與預測兩個方面也均具有較好的性能，整體上優(yōu)于其他模型. 后續(xù)研究中，還應該深入鉆研軟件排錯過程中的隨機性（包括多個測試階段內的延遲、多種測試覆蓋類型函數等），以及針對大型開源軟件和復雜網絡軟件的測試階段可靠性建模與評測，同時要采用人工神經網絡、遺傳算法和隨機過程等數學工具建立更加精準的驗證模型.

參考文獻

[1] ? ?HUANG C Y ，HUANG W C . Software reliability analysis and measurement using finite and infinite server queueing models[J]. IEEE Transactions on Reliability，2008，57（1）：192—203.

[2] ? ?許家俊，姚淑珍. 軟件可靠性增長模型的不確定性量化研究[J]. 軟件學報，2017，28（7）：1746—1758.

XU J J，YAO S Z. Characterizing uncertainty of software reliability growth model[J]. Journal of Software，2017，28（7）：1746—1758. （In Chinese）

[3] ? ?WANG J Y，ZHANG C. Software reliability prediction using a deep learning model based on the RNN encoder-decoder[J]. Reliability Engineering & System Safety，2018，170（2）：73—82.

[4] ? ?PENG R，MA X Y，ZHAI Q Q，et al. Software reliability growth model considering first-step and second-step fault dependency[J]. Journal of Shanghai Jiaotong University （Science），2019，24（4）：477—479.

[5] ? ?LI Q，PHAM H. A generalized software reliability growth model with consideration of the uncertainty of operating environments[J]. IEEE Access，2019，7：84253—84267.

[6] ? ?王金勇，張策，米曉萍，等. Weibull分布引進故障的軟件可靠性增長模型[J]. 軟件學報，2019，30（6）：1759—1777.

WANG J Y，ZHANG C，MI X P，et al. A software reliability growth model based on Weibull distribution introduced faults[J]. Journal of Software，2019，30（6）：1759—1777 .（In Chinese）

[7] ? ?米曉萍，王金勇. 考慮排錯過程引進故障的開源軟件可靠性模型研究[J]. 計算機應用研究，2019，36（7）：2070—2080.

MI X P，WANG J Y. Software reliability models for open source software considering correction process and fault introduction[J].Application Research of Computers，2019，36（7）：2070—2080. （In Chinese）

[8] ? AGGARWAL A G，GANDHI N，VERMA V，et al. Multi-release software reliability growth assessment：an approach incorporating fault reduction factor and imperfect debugging[J]. International Journal of Mathematics in Operational Research，2019，15（4）：446—463.

[9] ? ?KAPUR P K，PHAM H，ANAND S，et al. A unified approach for developing software reliability growth models in the presence of imperfect debugging and error generation[J]. IEEE Transactions on Reliability，2011，60（1）：331—340.

[10] ?SINGH O，KAPUR R，SINGH J，Considering the effect of learning with two types of imperfect debugging in software reliability growth modeling[J]. Communications in Dependability and Quality Management，2010，13（4）：29—39.

[11] ?SARAF I，LQBAL J. Generalized multi‐release modelling of software reliability growth models from the perspective of two types of imperfect debugging and change point[J].Quality & Reliability Engineering International. 2019，35（7）：2358—2370.

[12] ?SARAF I，LQBAL J. Generalized software fault detection and correction modeling framework through imperfect debugging，error generation and change point[J]. International Journal of Information Technology，2019，11（4）：751—757.

[13] ?張 策，孟凡超，考永貴，等. 軟件可靠性增長模型研究綜述[J]. 軟件學報，2017，28（9）：2402—2430.

ZHANG C，MENG F C，KAO Y G，et al. Survey of software reliability growth model[J]. Journal of Software，2017，28（9）：2402—2430.（In Chinese）

[14] ?ALMERING V，VAN GENUCHTEN M，CLOUDT G，et al. Using software reliability growth models in practice[J]. IEEE Software，2007，24（6）：82—88.

[15] ?ERTO P，GIORGIO M，LEPORE A. The generalized inflection S-shaped software reliability growth model[J]. IEEE Transactions on Reliability，2020，69（1）：228—244.

[16] ?GOSEVA-POPSTOJANOVA K，TRIVEDI K S. Failure correlation in software reliability models[J]. IEEE Trans on Reliability，2000，49（1）：37—48.

[17] ?AHMAD N，KHAN M G M，RAFI L S. A study of testing-effort dependent inflection S-shaped software reliability growth models with imperfect debugging[J]. International Journal of Quality & Reliability Management，2010，27（1）：89—110.

[18] ?GOEL L，OKUMOTO K. Time-dependent error-detection rate model for software reliability and other performance measures[J]. IEEE Transactions on Reliability，1979，R-28（3）：206—211.

[19] ?SAMEERA M S，KANCHARLA G R，PRASAD R S. Software reliability measurement using combined Goel OKUMOTO and ANOM perfect debugging model[J]. Journal of Advanced Research in Dynamical and Control Systems，2019，11（S）：780—787.

[20] ?CHIU K C，HUANG Y S，LEE T Z. A study of software reliability growth from the perspective of learning effects[J]. Reliability Engineering & System Safety，2008，93（10）：1410—1421.

[21] ?HUANG C Y，LYU M R，KUO S Y. A unified scheme of some nonhomogenous poisson process models for software reliability estimation[J]. IEEE Transactions on Software Engineering，2003，29（3）：261—269.

[22] ?PHAM H. Software reliability and cost models：perspectives，comparison，and practice[J]. European Journal of Operational Research，2003，149（3）：475—489.

[23] ?PHAM H，NORDMANN L，ZHANG X. A general imperfect-software-debugging model with S-shaped fault-detection rate[J]. IEEE Transactions on Reliability，1999，48（2）：169—175.

[24] ?WOOD A. Predicting software reliability[J]. Computer，1996，29（11）：69—77.

[25] ?NAGARAJU V，WANDJI T，FIONDELLA L. Improved algorithm for non-homogeneous poisson process software reliability growth models incorporating testing-effort[J].International Journal of Performability Engineering. 2019，15（5）：1265—1272.

[26] ?PHAM T，PHAM H. A generalized software reliability model with stochastic fault-detection rate[J]. Annals of Operations Research，2019，277（1）：83—93.

[27] ?PHAM H，ZHANG X M. NHPP software reliability and cost models with testing coverage[J]. European Journal of Operational Research，2003，145（2）：443—454.

[28] ?ANNIPRINCY B，SRIDHAR S. An efficient software reliability growth models with two types of imperfect debugging[J]. European Journal of Scientific Research，2012，72（4）：490—503.

[29] ?鄒北驥，張保國，李軍義，等. 基于形式規(guī)約的軟件測試用例自動生成技術研究[J].湖南大學學報（自然科學版），2004，31（3）：81—85.

ZOU B J，ZHANG B G，LI J Y，et al. Research on automatic test case generation based on form specification[J]. Journal of Hunan University （Natural Sciences），2004，31（3）：81—85. （In Chinese）

[30] ?GOKHALE S S，PHILIP T，MARINOS P N，et al. Unification of finite failure non-homogeneous Poisson process models through test coverage[C]//Proceedings of ISSRE'96：7th International Symposium on Software Reliability Engineering. IEEE，1996：299—307.

[31] ?YAMADA S，TOKUNO K，OSAKI S. Imperfect debugging models with fault introduction rate for software reliability assessment[J]. International Journal of Systems Science，1992，23（12）：2241—2252.

[32] ?PHAM H，ZHANG X. An NHPP software reliability model and its comparison[J]. International Journal of Reliability，Quality and Safety Engineering，1997，4（3）：269—282.

[33] ?ZHANG X，TENG X，PHAM H. Considering fault removal efficiency in software reliability assessment[J]. IEEE Transactions on Systems，Man and Cybernetics，Part A：Systems and Humans，2003，33（1）：114—120.

[34] ?OHBA M，CHOU X M. Does imperfect debugging affect software reliability growth？[C]// Proceedings of the 11th International Conference on Software Engineering. Pittsburgh，PA，USA：ACM，1989：237—244.

[35] ?STRINGFELLOW C，ANDREWS A A. An empirical method for selecting software reliability growth models[J]. Empirical Software Engineering，2002，7（4）：319—343.

[36] ?ZHANG X，PHAM H. Software field failure rate prediction before software deployment[J]. Journal of Systems and Software，2006，79（3）：291—300.

[37] ?ZHANG C，CUI G，BIAN Y L，et al. Component-based software reliability process simulation considering imperfect debugging[J]. High Technology Letter，2014，20（1）：9—15.

收稿日期：2020-04-19

基金項目：國家自然科學基金資助項目（61473097），National Natural Science Foundation of China（61473097）;山東省重點研發(fā)計劃項目（GG201703130116，GG201703040002），Key Research and Development Project of Shandong Province（GG201703130116，GG201703040002）;威海市科技發(fā)展計劃項目（ITEAZMZ001807），Weihai Science and Technology Development Plan Project（ITEAZMZ001807）

作者簡介：張策（1978—），男，吉林永吉人，哈爾濱工業(yè)大學副教授，博士，碩士生導師

通信聯(lián)系人，E-mail：zhangce@hitwh.edu.cn