戲說復變函數閉路積分

（西安工業大學 陜西·西安 710032）

復變函數是高等院校工科專業的一門專業基礎課，在其后續的專業課中有著廣泛的應用。復變函數主要的研究對象是解析函數，而復變函數的積分是研究解析函數的重要工具，因此學好復變函數的積分特別是閉路積分成為了一個亟待解決的問題。但課程本身由于內容抽象，知識點多，部分同學數學底子差等，所以導致學習效果并不盡如人意。為了提高同學的學習興趣，使得同學們對知識更容易識記，本文嘗試在“戲說方式下創造一個的情景”，引入復變函數閉路積分的各種方法，并附以相應的例題，并且分析了“積分方法一家子”的區別和聯系，以幫助進一步加深理解和記憶，從而輕松解決閉路積分的相關問題。

1 復變函數閉路積分方法“群英會”

話說復變函數的閉路積分，真可謂方法眾多、功能各異，他們就如那“八仙過海，各顯神通”，在積分計算的大舞臺上大放著異彩。

其中龍頭老大當屬柯西-古薩（定理）（也稱柯西積分定理），它獨樹一幟，做事干脆利索。管你被積函數形式再復雜，猴子猴孫（被積函數的奇點）再多，只要你不犯我地盤（奇點不落在積分路徑內），我決定放你一馬，多余的功夫跟你不費，結果為0，一遍好好歇著！

柯西-古薩定理：

積分路徑有一奇點？哈哈，你還敢來煩老大——柯西-古薩（定理）？好自為之，趕緊繞道吧（柯西-古薩定理不再適用）。那誰來替俺主持公道（那咋算）？哼哼，江湖自有英雄！

積分方法1：迎面走來“例題哥”（典例結果）

嗯，例題哥在那弄啥咧？莫非相親嗎？大哥快來！柯西積分公式大聲呼叫高導公式：咱也湊湊熱鬧，打個擂臺，看看俺們行不行？

積分方法2：打扮好（變了形）的柯西積分公式精彩亮相：

積分方法3：換了造型（變了形）的高導公式盛裝出席：

恁倆啊？說中也中，說不中也不中；有時中，有時不中；要看對象是誰咧。

啥？還有比俺們高的神？

積分方法4：羅朗展式法。

例3還可以用如上留數規則1計算（其實柯西積分公式與其一致，但此處更容易，因為不需要對被積函數進行變形整理）。

留數計算規則2（m級極點）：

積分方法6：

例4還可以用如上留數規則2計算。（其實高導公式與其一致）

例3還可以用如上留數規則3計算（比柯西積分公式和留數規則1更容易，因為不需要對被積函數進行變形整理，另外計算更簡便，且本質上是一回事）。厲害了，額滴那個神啊！

神仙偶爾也失手，你來看看有沒有？

路徑里面多奇點，只能復合閉路“挖奇點”，加上積分的留數新知識，剛好整出積分計算之留數兩定理。留數定理一上場，從此積分它最響（盡量都用留數方法做）。內部不行轉外部，無窮遠點留數（規則4）來幫助。這種方法好處多（方法指的是留數定理并留數計算規則），簡便易行少繁瑣（不用“挖奇點”）；這種方法思路闊，所有積分都能做。

積分計算方法8留數定理+規則4：

山外青山樓外樓，無窮遠點（的留數法）你最牛。

哈哈，兄弟們！有緣千里來相會，贊來贊去也不是個事兒！

其實咱們都是一家子，所以千萬別客氣。為求積分聚一起，奇點在哪是大問題：

路徑內部無奇點，柯西-古薩最長臉。路徑內部一奇點，積分方法腦海閃。

路徑內部多奇點，留數定理來幫咱。各種方法來列隊，積分不再是個事（兒）。

2 聊聊復變函數閉路積分方法的“一家子”

說復變函數閉路積分方法都是一家子，其實是因為復變函數閉路積分的幾種方法相互之間都有著緊密的聯系，有的甚至是一回事。在授課過程中，我們是這樣處理的，在柯西-古薩定理的基礎上推出了復合閉路定理；利用復合閉路定理和“例題哥”結果引出了柯西積分公式的思考，并在復合閉路的基礎上證明了柯西積分公式；根據柯西積分公式證明高階導數公式；“例題哥”又是柯西積分公式和高導公式的特殊情況（被積函數分子為1）；在高導公式的基礎上，推出了解析函數的泰勒級數和洛朗級數；并對解析函數的羅朗展式兩端進一步進行積分探討，引出了留數定義；并利用復合閉路定理給出了復變函數閉路積分的留數定理；從此就將復變函數的積分運算轉化成了留數的計算；緊接著根據孤立奇點的分類，進一步探討了留數計算的四個常用規則。當積分路徑內部只有一個奇點時，柯西積分公式計算積分跟利用“留數定理和規則1”計算是一回事；高導公式計算積分跟利用“留數定理和規則2”計算也是一回事。特別是當積分路徑內多奇點時，利用留數定理和幾個規則聯合處理，就省去了“挖奇點”或者利用柯西積分公式和高導公式常常要把被積函數對著適用的函數特征進行整理的麻煩；特別是連同無窮遠點處的留數一起切切實實解決了前面的那些方法在某些問題上不能解決的麻煩。

舉例說明柯西積分公式與“留數定理+規則1”的一致性，如下：

當積分路徑內部有唯一奇點且是一級時，可以用柯西積分公式，也可以利用留數定理+規則1的計算方法。這里要注意公式和定理中的被積函數的書寫形式，原來定理中符號雖然一樣，其實意義不同，這里區分開來，后者用表示，因為是被積函數的一級極點，所以可以寫成這樣的形式，，所以有：

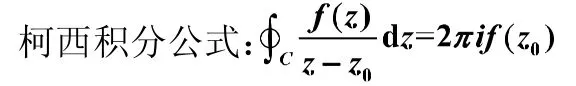
留數定理+規則1：

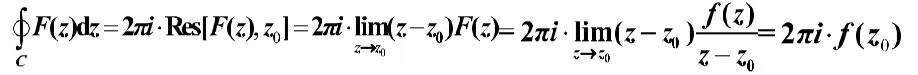
由此看見兩者是一致的。

3 小結

文中在戲說各種閉路積分方法時，采取情景化的模式，自然引出各個積分方法和對應的例題分析，并進一步分析了各種方法之間的聯系，理清了方法的本質，分析了各方法的優劣。總之，在積分計算時，當積分路徑內部沒有奇點時，利用柯西-古薩定理直接結果為0；當積分路徑內部有奇點時，不管一個還是多個，最好采取“留數定理+留數計算規則”的各種組合模式。當然了，有的同學可能會先入為主，喜歡用前面的積分方法也是可以的，總之，多記一些方法和例題，認真分析和揣摩，舉一反三才能順利應對各種復變函數閉路積分計算的問題。