基于離散余弦變換的單像素相機測量矩陣的性能評估

程 濤，吳小龍，楊 明

(廣西科技大學機械與交通工程學院,廣西 柳州 545006)

0 引言

根據壓縮感知(compressed sensing, CS)理論可知，如果信號是稀疏的就能以遠低于奈奎斯特(Nyquist)采樣頻率的采樣率采集信號，并能高概率精確恢復信號[1-4]。但是，電、光、聲、磁、熱和機械等一維、二維或多維信號多非稀疏，可壓縮。可壓縮信號需做稀疏變換，才能滿足壓縮感知的稀疏化要求[4-6]。基于可壓縮信號的壓縮感知數學模型如式(1)所示：

min‖α‖0s.t.y=ΦΨTα(x=ΨTα,ΦR=ΦΨT)

(1)

式(1)中：y是測量信號，y∈RM；Φ是測量矩陣，Φ∈RM×N；Ψ是稀疏變換基，Ψ∈RN×N；x是可壓縮信號，x∈RN；α為x的稀疏變換域系數，α∈RN；ΦR為重構矩陣；M是測量矩陣的行數，N為測量矩陣的列數[7-8]。壓縮感知主要分為數據采集壓縮的測量階段和數據解壓恢復的重構階段。在測量階段，通過測量矩陣Φ采集得到測量數據y；在重構階段，通過式(1)解算得到稀疏變換域系數α，通過逆變換從而求得信號x[3,8]。

常用的測量矩陣有高斯矩陣、哈達瑪矩陣和伯努利矩陣等。這些矩陣盡管能很好滿足壓縮感知的約束等距性要求，但多為稠密矩陣，元素所需存儲空間大[9-10]；而且由于其非結構化的本質導致計算復雜度高，不利于編程和硬件實現。對于可壓縮信號，重構矩陣性能的好壞與稀疏變換基和測量矩陣有關。文獻[11—12]在稀疏變換基已經確定的情況下，以列相關性最小化或平均化為目標來優化重構矩陣，得到優化后的重構矩陣。盡管經過優化的重構矩陣有更好的重構能力，但是對應的測量矩陣已不是原來的測量矩陣，實用價值不高。針對稀疏信號，基于0-1循環矩陣提出的測量矩陣優化算法實現了在測量階段采用事先確定的測量矩陣采集測量數據，在重構階段采用優化后的測量矩陣重構稀疏信號，取得了很好的效果[13]。

基于數字微鏡(digital micromirror device,DMD)的單像素相機采用的0-1隨機矩陣盡管易于硬件實現且所需存儲空間小[4,14-15]，但在利于編程和運算速度方面依然不如0-1循環矩陣。離散余弦變換(discrete cosine transform, DCT)是影像和視頻壓縮中廣泛使用的通用技術[8]。DCT除了具有正交變換性，還能很好地描述可壓縮信號的相關特征。對于可壓縮信號，壓縮感知的重構效果不但受到測量矩陣的影響，也取決于稀疏變換基與測量矩陣的相互作用。因此，本文以DCT矩陣作為式(1)的稀疏變換基，以單像素相機的0-1隨機矩陣[4,14]和0-1循環矩陣作為式(1)的測量矩陣，在驗證檢驗矩陣優化算法通用性的同時，開展單像素相機測量矩陣的比較評估。進而理論分析稀疏變換基與測量矩陣的相互作用機理。

為便于與已有文獻對比，測量矩陣大小設置為128×256。0-1循環矩陣初始行向量為32個隨機分布的1，每一行向量都是前一行向量各元素右移兩位的結果。0-1隨機矩陣各行向量包含32個隨機分布的1。

1 基于不同測量矩陣的重構矩陣優化前后的性能對比

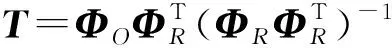
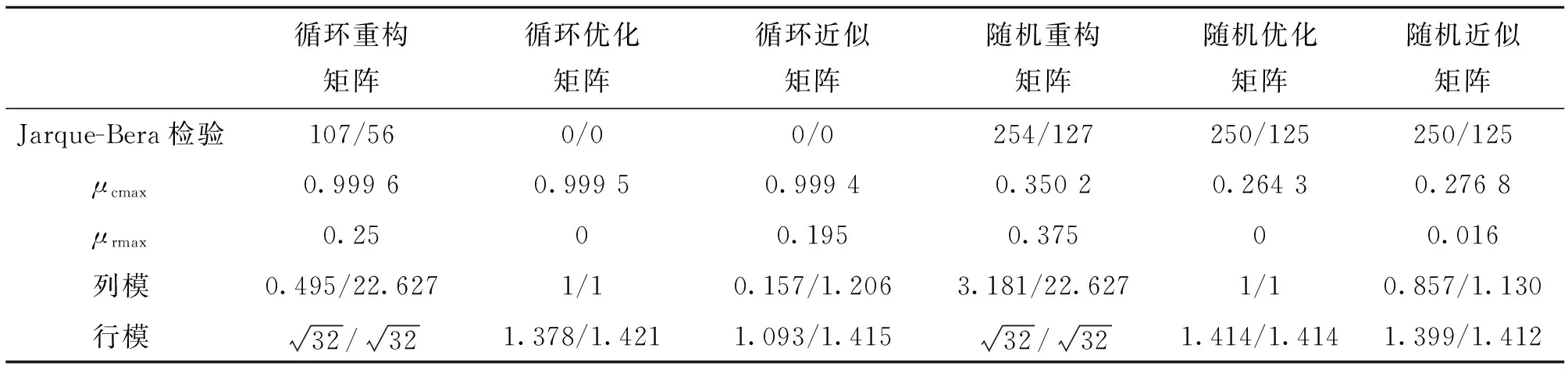
表1 6類矩陣的相關參數Tab.1 Parameters of 6 matrices

表1為測量矩陣分別采用0-1循環矩陣和0-1隨機矩陣，稀疏變換基采用DCT矩陣，n=100次時相應重構矩陣、優化矩陣和近似矩陣的各種統計參數。Jarque-Bera檢驗這一行“/”左邊的數據表示服從高斯分布的列數；“/”右邊的數據表示服從高斯分布的行數。μcmax表示各列間相關系數絕對值的最大值；μrmax表示各行間相關系數絕對值的最大值。行模和列模這兩行中“/”左邊表示最小值，“/”右邊表示最大值。

根據文獻[8,13]可知，經過行向量正交規范化和列向量單位化的優化矩陣和近似矩陣的性質與高斯矩陣相近，具備高斯矩陣對各類稀疏信號的普適性。本文以此為依據，通過圖1—圖4比較分析循環重構矩陣和隨機重構矩陣在迭代優化過程中的優化矩陣和近似矩陣的性質變化。

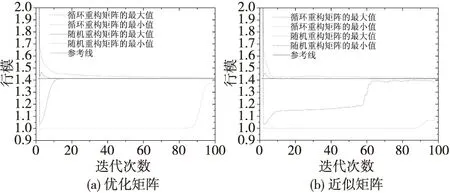
圖1 基于循環重構矩陣和隨機重構矩陣的優化矩陣和近似矩陣的行模極值與迭代次數的關系Fig.1 Row norms extreme value of optimization matrix and approximate matrix based on circulant reconstruction matrices and random reconstruction matrices vs. iteration

由圖2(a)可知，隨機優化矩陣的列相關系數絕對值最大值和行相關系數絕對值最大值在第3次迭代后收斂，列相關系數絕對值最大值接近于0.26，行相關系數絕對值最大值接近于0；循環優化矩陣的列相關系數絕對值最大值接近于1，行相關系數絕對值最大值接近于0。由圖2(b)可知，隨機近似矩陣的列相關系數絕對值的最大值在第3次迭代后收斂，接近于0.27，行相關系數絕對值最大值在第62次迭代后收斂，接近于0；循環近似矩陣的列相關系數絕對值的最大值接近于1，行相關系數絕對值的最大值在第95次迭代后接近于0.2。隨機優化和近似矩陣的不相關性都好于循環優化和近似矩陣。

圖2 基于循環重構矩陣和隨機重構矩陣的優化矩陣和近似矩陣的列相關系數的絕對值最大值與迭代次數的關系Fig.2 Maximum value of absolute value of the row and column correlation coefficient of optimization matrix and approximate matrix based on circulant reconstruction matrices and random reconstruction matrices vs. iteration

由圖3(a)可知，隨機優化矩陣服從高斯分布的列和行在第62次迭代后收斂，服從高斯分布的列數接近于250，服從高斯分布的行數接近125；循環優化矩陣服從高斯分布的列數和行數在第2次迭代后迅速收斂于0。由圖3(b)可知，隨機近似矩陣服從高斯分布的列數和行數在第62次迭代后收斂，服從高斯分布的列數接近250，服從高斯分布的行數接近125；循環近似矩陣服從高斯分布的行數和列數在第2次迭代后迅速收斂于0。隨機優化和近似矩陣服從高斯分布的行列數都好于循環隨機和近似矩陣。

由圖4可知，隨機近似矩陣列模的極大值和極小值在第5次迭代后收斂，極大值接近于1.1，極小值接近于0.9；循環近似矩陣的列模的極大值在第3次迭代后收斂于1.2，最小值收斂于0.15，相差較大。隨機優化和近似矩陣的列模的收斂性都好于循環優化和近似矩陣，前者更接近于1。由圖1—圖4可見，隨機優化和隨機近似矩陣的性能都好于循環優化和循環近似矩陣的性能。

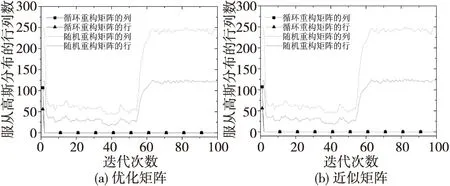
圖3 基于循環重構矩陣和隨機重構矩陣的優化矩陣和近似矩陣的服從高斯分布的行列數與迭代次數的關系Fig.3 Number of row and column which follows the Gaussian distribution of optimization matrix and approximate matrix based on circulant reconstruction matrices and random reconstruction matrices vs. iteration

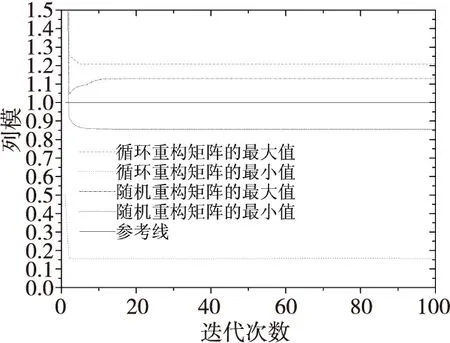
圖4 循環和隨機重構矩陣的近似矩陣各列模極值與迭代次數的關系Fig.4 Column norm extremum value of approximate matrix of circulant and random reconstruction matrices vs. iteration

2 稀疏變換基與測量矩陣的相互作用

圖5是循環和隨機重構矩陣的灰度圖。隨機重構矩陣的灰度圖依然保持很好的隨機性；循環重構矩陣的灰度圖呈左右對稱結構。即使只取循環重構矩陣的左半部分或右半部分，甚至各半部分的1/4來研究，其μcmax也達到0.7，各列高度相關。測量矩陣與稀疏變換基的轉置矩陣相乘就可得到重構矩陣。DCT是一種空間域的低通濾波器，可將信號從空間域轉換到頻率域。DCT相當于長度約是它兩倍的離散傅里葉變換，是特殊的離散傅里葉變換。采用DCT矩陣作為稀疏變換基時，測量矩陣與稀疏變換基的轉置矩陣相乘，在物理幾何意義上等價于對測量矩陣各行作一維離散余弦變換。0-1循環矩陣是確定性矩陣，每一行向量都是前一行向量各元素循環移位的結果。各行元素順序結構相似。重構矩陣的各行就是測量矩陣各行作離散余弦變換后的稀疏變換域系數。這些稀疏變換域系數在不同頻域反映著0-1循環矩陣各行向量的順序結構信息。從而導致循環重構矩陣各列高度相似。即使對循環重構矩陣做優化也不能提高其隨機性，各列依然高度相關(如表1和圖1—圖4所示)。由此可見，稀疏變換基與測量矩陣的相互作用，對重構矩陣的性能有著重大的影響。0-1循環矩陣不宜和DCT矩陣組合為重構矩陣；但0-1隨機矩陣可和DCT矩陣組合為重構矩陣。

圖5 循環和隨機重構矩陣的灰度圖Fig.5 Grayscale image of circulant and random reconstruction matrices

3 基于不同測量矩陣的重構矩陣優化前后的重構效果

為進一步驗證循環重構矩陣及其優化和近似矩陣的性能，分別用循環重構矩陣和隨機重構矩陣及其優化和近似矩陣對高斯稀疏信號采用正交匹配追蹤(orthogonal matching pursuit,OMP)算法重構。對每個稀疏度的信號在MatlabR2015b中重復試驗500次，計算準確重構概率，如圖6所示。

當測量矩陣為0-1隨機矩陣時，隨機優化矩陣和隨機近似矩陣的信號重構概率明顯好于隨機重構矩陣；當測量矩陣為0-1循環矩陣時，循環優化矩陣和循環近似矩陣的信號重構概率不但不明顯好于循環重構矩陣，而且3個矩陣的重構概率都小于1。

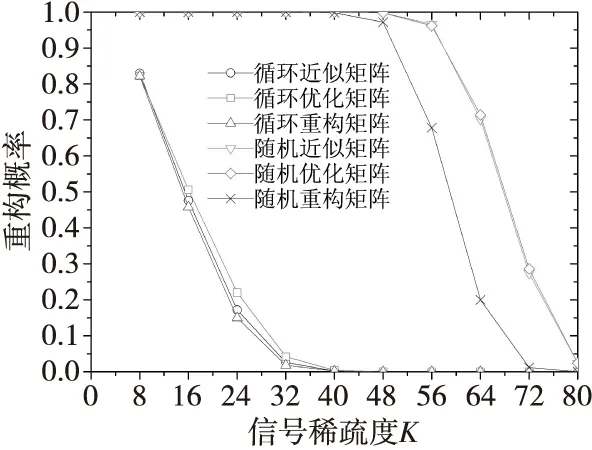
圖6 6種矩陣的信號準確重構概率與稀疏度關系Fig.6 Prob. of exact recovery vs. the sparsity by 6 matrices

4 結論

基于DMD的0-1循環矩陣易于編程和硬件實現，但是當單像素相機采集可壓縮信號時，測量矩陣與稀疏變換基相互作用，導致重構矩陣性能很差，即使使用矩陣優化算法也不能有效改善其性能。對比分析了以DCT為稀疏變換基的基于0-1隨機矩陣和0-1循環矩陣的重構矩陣，及其優化前后的重構效果。研究發現：單像素相機不能使用0-1循環矩陣作為測量矩陣，可使用0-1隨機矩陣作為測量矩陣，并能對相應重構矩陣做有效優化。同時給出了測量矩陣和稀疏變換基作用機理的理論解釋。為單像素相機測量矩陣的選型和設計提供了方向指導，利于設計制造出性能更優的單像素相機。