考慮休班公平及同班次約束的呼叫中心排班優化問題
胡修武,徐 悅,王秀利
(南京理工大學經濟管理學院,江蘇南京210094)
1 引 言
呼叫中心(Call Center/Contact Center)是通過電話等電信媒介手段為顧客提供產品售后支持、訂購交易等服務的組織實體.呼叫中心屬于勞動密集型行業,人力成本占運營成本的70%左右;呼叫中心人力運作管理引起了學術界廣泛研究興趣[1,2].近年來,隨著更多制造商專注于核心業務能力提升而愿意把產品售后電話服務外包出去,國內從事呼叫服務業務的呼叫中心企業越來越多,行業規模擴展迅速[3].實際調研發現,呼叫中心企業面臨著年輕員工自我意識強、對工作條件及環境要求較高和離職率居高不下等情況.坐席人力排班時,企業除了考慮勞動法規合同要求,越來越注重納入人性化管理因素來提高員工滿意度,從而有助于提升服務效率.
呼叫中心人力運作管理研究大致可分為人力需求計算、路由策略和人力排班.人力需求計算或路由策略研究成果很多,而呼叫中心排班問題研究相對較少[4?7].最近,Defraeyen和van Nieuwenhuyse對呼叫中心排班問題研究成果進行綜述[7].一些呼叫中心排班問題研究假設計劃周期為日期,考慮日內各種實際場景因素,如坐席人員多技能[8,9]、區段人力需求隨機動態性[10]、各班次不同成本及交叉培訓成本[11]、或連續區段人力需求關聯性[12]等,構建坐席人員排班問題(隨機)整數規劃模型,并分別提出最優算法以及啟發式或智能算法.這些研究因計劃周期是日期,不涉及員工休班及不同日期班次關聯等決策問題.也有少數學者研究計劃周期為單周的呼叫中心排班問題,構建整數規劃模型并提出優化算法[13,14].與行業內文獻[13,14]不同,本文研究明確納入了雙休日休班公平性考慮,并通過同班次用工約束來保證員工上班規律性.我們注意到,近些年來其它行業(如醫療[15?17]、運輸物流[18,19]和零售[20]等)的人力排班研究中,考慮了雙休日休班或其它方式的排班公平性.不難看出,呼叫中心行業在用工規定、業務需求分布和人力班次結構等方面與這些行業不同.盡管本文排班問題也同樣納入雙休日休班公平性等因素,但呼叫行業本身特點決定了研究模型方法不同于這些行業人力排班問題.
與國外同行業普遍周薪制不同,國內呼叫中心通常實行月薪制,通過編制月度排班表對坐席人力進行計劃管理.班表編制時,通過保證雙休日休班公平和周內同班次當班來體現企業人性化管理理念.針對該實際排班場景,本文給出了制定排班方案的優化模型和方法,并且量化分析了這些人性化管理因素對人力成本控制的影響.本文創新性體現在兩方面,一是通過分析推導,取得了反映排班問題優化規律的一些理論結果;二是在借鑒已有研究成果基礎上,通過利用問題本身結構和優化性質,提出了求解排班方案的優化模型和算法.實例計算驗證了排班模型和算法的有效性;研究表明在兼顧休班公平性和上班規律性情況下,仍能夠對排班人力成本進行有效控制.
2 坐席人員排班模型
研究的排班問題中,假設用工制度除了反映國內勞動法規要求,還包括以下兩點體現人性化管理的約束因素.首先,基于生活、社交和子女教育等原因,大多數員工愿意雙休日休班.為了照顧員工生活方便性及體現公平性,排班時在班表周期內要保證每個員工雙休日休班不少于規定次數.其次,由于坐席人員排班的復雜性,手工排班經常致使周內當班班次不同的員工占比偏高.當班班次頻繁切換對員工工作及生活具有很大負面影響.為了保證工作時間規律性,規定每個員工周內工作日同班次當班.
本文排班問題具體描述為,在滿足服務水平指標要求和企業用工制度約束情況下,確定連續4周內坐席人員當班與休班日期,以及當班日期班次,使得坐席人員使用數量最少(即優化人力成本).具體說明如下.
呼叫服務系統可用排隊論模型來描述,其中假設顧客電話到達率服從泊松分布,坐席人員服務率服從指數分布.服務水平指標通常采用隊列中顧客呼入電話在給定等待時間內接通的百分率(Telephone Service Factor,TSF)刻畫.給定服務指標TSF,使用排隊論方法Erlang C可計算出達到指標TSF需要的最少坐席人員數量[1,2,7].目前,Erlang C 因簡單易用,仍然是最為廣泛使用的人力需求計算方法.該方法由于沒有考慮服務隊列中的棄話現象,計算的人力需求往往偏大.若考慮隊列棄話現象并假設顧客耐心時間服從指數分布,就是模型Erlang A.很多學者推薦使用Erlang A來計算坐席人力需求[2,7,14].本文采用Erlang A計算坐席人力需求,用計算出的最少坐席人員需求數量來刻畫服務指標TSF要求.
企業用工制度既反映國內勞動法規合同要求,也體現企業自身管理偏好.本文假設用工制度包括,S1:員工每周當班天數不應超過5天,每天最多1 個班次當班.S2:員工4 周內至少1 個雙休日休班.S3:員工雙休日兩天要么全當班,要么全休班.S4:員工周內工作日當班班次相同,不同周當班班次可以不同.約束S1反映國內勞動法規對員工休班天數的規定.在4周排班表中,由于每周雙休日總需要安排部分員工當班來提供呼入話務服務,盡管大多數員工愿意雙休日休班,客觀上只能安排部分員工雙休日休班.規定S2通過保證每個員工至少1個雙休日休班來體現周末休班公平性.規定S3既反映員工雙休日完整休班意愿,又方便企業安排更多員工雙休日休班.其它行業人力排班研究中也考慮了用工規定S2 和S3(如見綜述文獻[19]).規定S4保證員工周內上班時間規律性,有助于提升員工服務效率.計劃周期假設為4個連續完整周,利用上述排班問題優化解,適當補充改動后很容易獲得月度排班優化方案.為了方便問題模型和算法描述,定義的參數與決策變量符號見表1.

表1 參數和決策變量說明Table 1 The description of parameters and decision variables
下面構建坐席人員排班優化問題的整數線性規劃模型(ILP1)
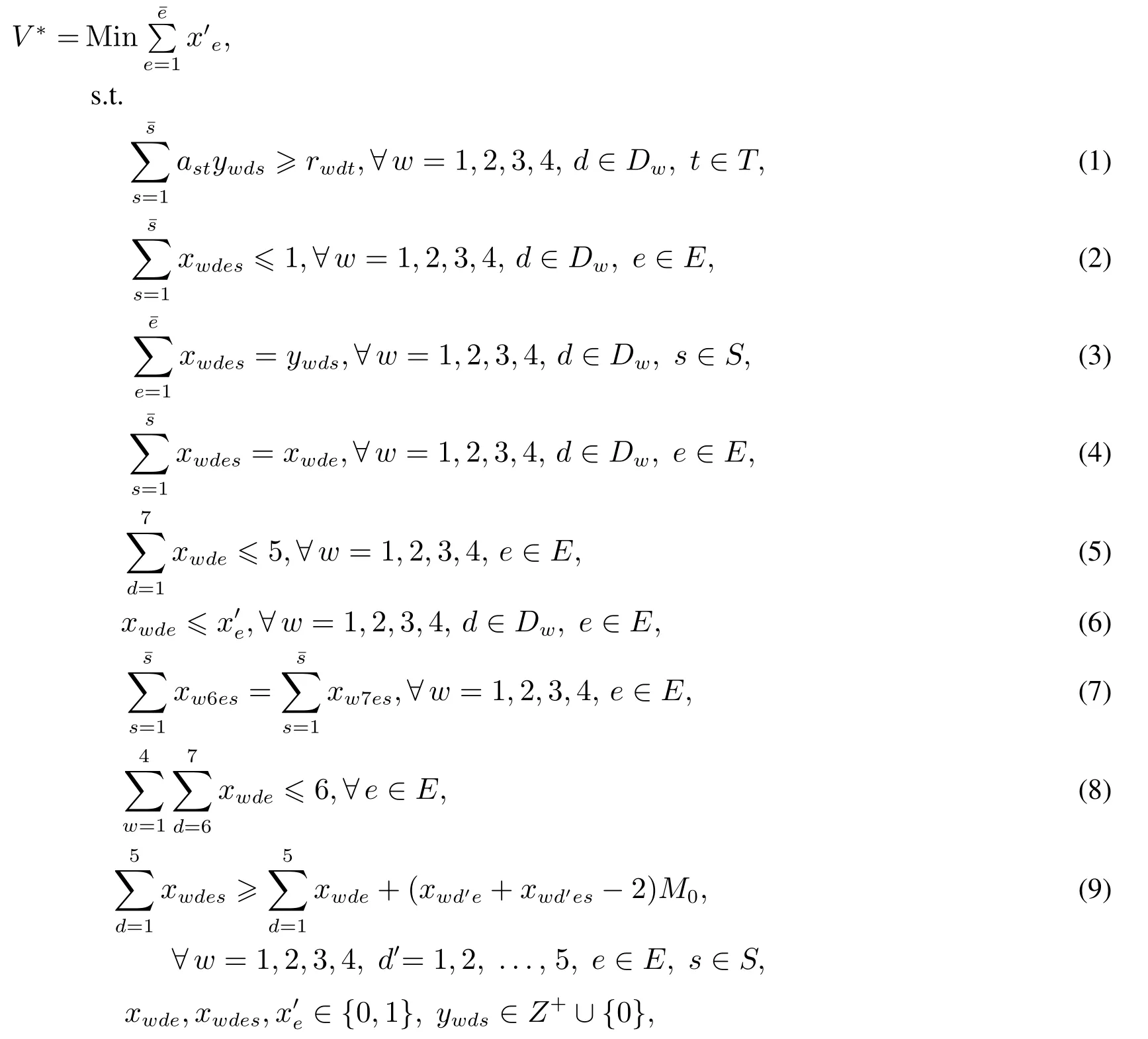
其中式(1)描述達到指標TSF要求的區段當班坐席人力.式(2)表示S1規定的員工每天最多1個班次當班.式(3)和式(4)描述決策變量之間關系.式(5)表示S1規定的員工周內當班天數限制.式(6)表示最優解方案中員工4周內至少當班1天.式(7)表示S3規定的員工雙休日要么全休班,要么全當班.式(8)(結合式(7))描述S2規定的4 周內員工至少1個雙休日休班.式(9)描述S4規定的員工在周內工作日同班次當班約束,式中M0取充分大正整數.每個員工e在周w內的工作日是否當班和周內當班班次均為決策變量,這意味著規定S4蘊含著可能出現的25|S|種同班次當班情況.對每個員工e,式(9)通過包含的5|S|個具體約束式(s ∈S和d′=1,2,...,5)來刻畫所有同班次當班情況.在5|S|個約束式中,至少存在1個式子以條件”某個班次當班天數不少于當班總天數”成立,來保證員工e滿足規定S4;而其它式子會因右邊第2項取充分小負整數,在邏輯上成立但不起約束作用.反之,如果員工e在周內當班班次不同,則在5|S|個約束式中總存在不能成立的式子.
3 問題分析
本節首先給出人力需求計算方法,然后分析坐席人力需求特征和推導問題優化性質.本文人力需求泛指基于呼入話務量的當班人力需求或納入用工制度約束后的坐席人員數量需求.
3.1 人力需求計算
呼叫服務系統中,呼入電話到達率或坐席人員處理時間都是隨機變量.當話務處理時間相對區段長度較短情況下,則系統在區段內會很快進入穩定狀態.在該情況下,可把每個區段的呼叫服務過程看作獨立馬爾科夫生滅過程(Markovian birth-death process),即滿足SIPP(stationary independent period-by-period)條件[1,2,14].若假設日期d內區段t的呼入電話到達率服從數學期望為λtd的泊松分布,std個坐席人員話務處理時間和顧客耐心時間分別服從數學期望為htd(服務率μtd=1/htd)和b的指數分布,則可用排隊論模型Erlang A 來近似計算坐席人力需求.
在馬爾科夫生滅過程中,令Ptd(n)表示在日期d的區段t內,呼叫服務系統有n個顧客的狀態概率,則下列關系式成立,即

式(10)和式(11)表明,隨著n增大,該生滅過程中的電話死亡率會逐漸超過出生率(到達率),從而會導致狀態概率以超過幾何速度變小.為了能夠顯式表達狀態概率,可在規定誤差范圍內,忽略高階狀態概率.把顧客等待隊列長度限定在上界為N的狀態空間內,使得被截去隊列長度大于N的狀態概率之和不會超過給定誤差ε.令ρ=λtd/{std/htd+(N ?std)/b},考慮如下關系式
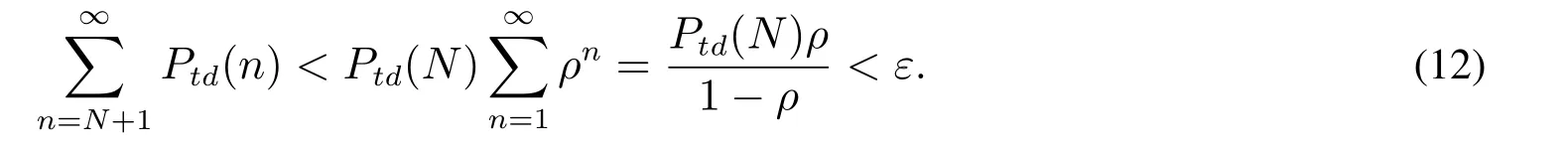
式(12)意味著只要確定充分大N,則能夠使得被截去狀態概率之和小于ε.確定N后,在隊列長度為0至N的狀態空間內,可重新歸一化計算概率(n),使得
在馬爾科夫生滅過程X={X(t)|t0}中,令Pr{W > τ|X=n}表示系統中有n個顧客情況下,顧客等待時長W超過給定時間τ的概率.Pr{W >τ|X=n}可根據下列定理計算.
定理1(見文獻[21])在馬爾科夫生滅系統中,對任意給定的τ >0,有
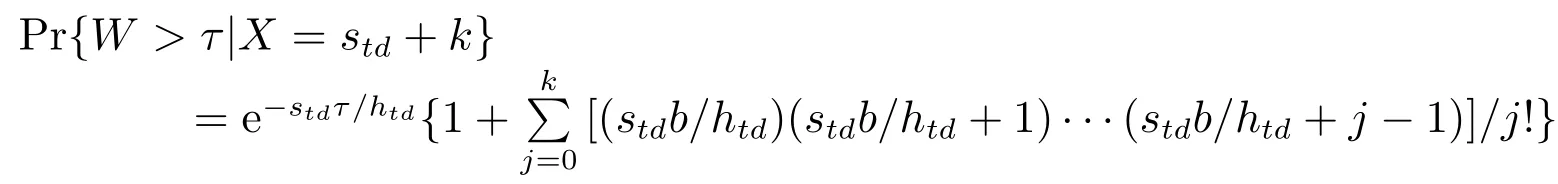
成立.
設Ltd表示日期d內區段t的服務指標TSF,即所有等待顧客在不超過時長τ內接通電話的百分占比.根據以上分析,則有
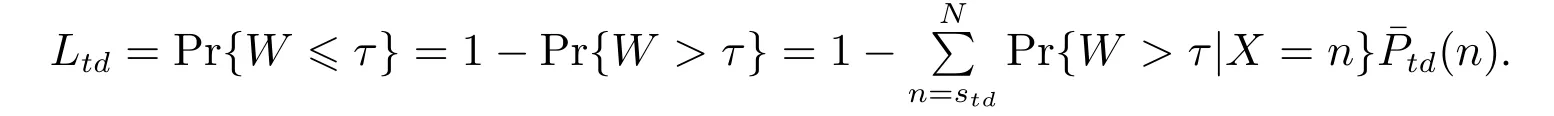
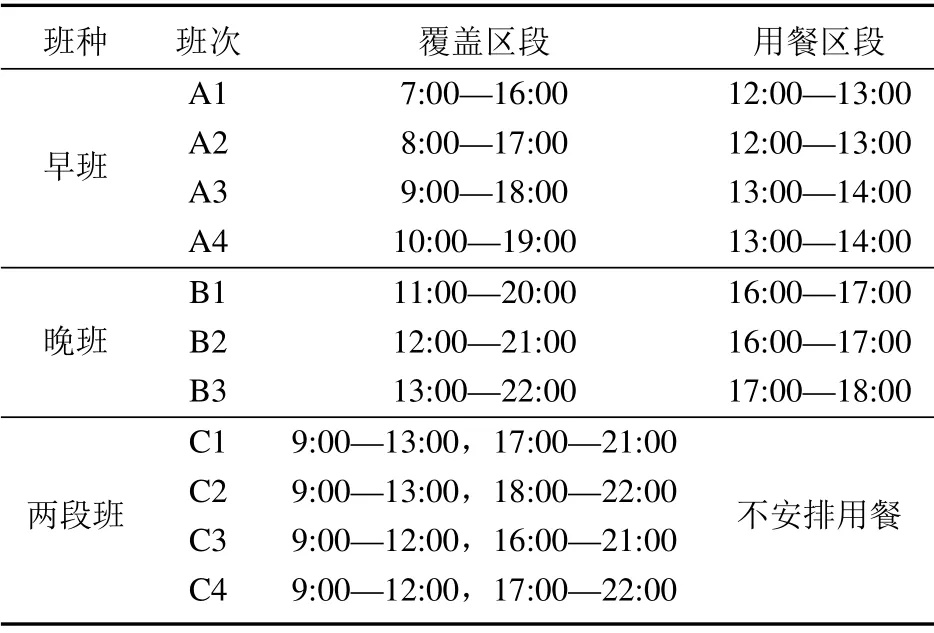
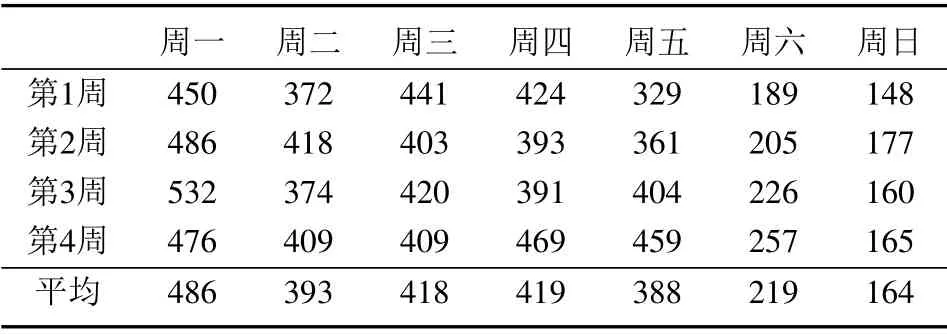
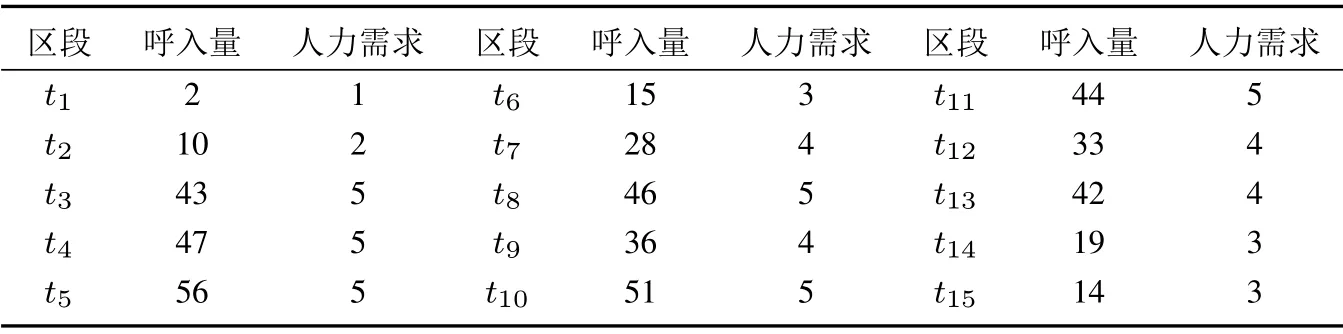
給定TSF指標Ltd,可計算需要最少坐席人員數量rtd如下:初始化,設坐席人員數rtd=和確定狀態概率截斷誤差ε(如10?5),計算出TSF指標L′td.若L′td 由于考慮休班和同班次等用工約束,問題模型ILP1求出的員工數量可能多于班表具體日期內所需要的坐席人力數量.下面首先通過構建整數規劃模型界定為了滿足話務服務指標要求而每日需要的最少坐席人力,然后通過分析每日最少坐席人力需求與排班周期內用工制度約束之間的關系,推導出問題ILP1下界. 令Q?wd表示在周w的日期d達到日內話務服務指標要求所需要的最少坐席人力,這里w=1,2,3,4和d=1,2,...,7.給定日內區段人力需求,則Q?wd可由下列整數規劃模型(ILP2)求出,即 令Aw6=Q?w6和Aw7=Q?w7.設Aw表示周w雙休日需要的最少當班坐席人員數量.考慮用工制度規定S3,則有Aw= max{Aw6,Aw7}.模型ILP2描述的日排班調度問題盡管與問題ILP1不同,但容易看出,模型ILP1最優解方案在周末日期d的排班結果也是該日期模型ILP2的可行解,從這個意義來說,模型ILP2求出的最優員工數量是模型ILP1的下界.進一步分析,根據用工制度規定S2,每個雙休日除了要安排一些員工當班來滿足日內所有區段人力需求,還可能要安排部分員工休班.同時考慮排班周期內4周雙休日當班和休班人力情況,可給出排班問題下界. 引理1問題最優目標值V ?滿足下列條件: 1)V ?max{A1,A2,A3,A4}; 2)V ?(A1+A2+A3+A4)/3,這里表示不小于“·”的最小整數. 證明1) 結論顯然成立.2) 令uw表示最優解中周w雙休日休班坐席人員數量.則對于w= 1,2,3,4,有V ?Aw+uw成立.故4V ?(A1+u1)+···+(A4+u4) = (A1+···+A4)+(u1+···+u4)成立.根據用工制度規定S2,則有u1+···+u4V ?成立.于是有3V ?A1+···+A4.考慮到V ?為整數,故結論2)成立.證畢. 若僅考慮每周內具體工作日人力需求,令Bwd表示周w工作日d需要的最少當班坐席人員數量,則Bwd=Q?wd,這里w= 1,2,3,4 和d= 1,2,...,5.由于規定S1要求每個員工周內雙休日或工作日至少休班2 天,同時考慮每周工作日當班和休班人力情況,可導出如下結論. 引理2問題最優目標值V ?滿足下列條件: 1)V ?max{Bwd|w=1,2,3,4;d=1,2,...,5}; 2)V ?[2Aw+(Bw1+···+Bw5)]/5,其中w=1,2,3,4. 證明1) 結論顯然成立.下面證明結論2).在問題最優解中,令uw和vw分別表示周w雙休日或工作日休班的坐席人員數量; 令uwd表示周w工作日d休班的坐席人員數量.對所有日期d= 1,2,...,5,V ?Bwd+uwd成立.于是,成立.注意到和V ?Aw+uw,有7V ?成立.考慮到每個坐席人員周內至少休班2天,且要么在雙休日休班,要么在工作日休班,故V ?uw+vw成立.因此,成立.注意到V ?,Aw和Bwd均為非負整數,故結論2)成立.證畢. 由模型ILP2求出最優解Aw6,Aw7和Bwd后,這里w= 1,2,3,4 和d= 1,2,...,5,根據引理1和引理2,可確定問題ILP1的下界,記為M. 如果不要求坐席人員周內工作日當值班次相同,即松弛用工制度S4,稱之為原問題ILP1的松弛問題.在模型ILP1中,去掉約束條件式(9)后,即為松弛問題整數規劃模型描述,記為SILP1.對于松弛問題SILP1,有如下結論. 定理2松弛問題SILP1最優解需要坐席人員數量為M. 證明明顯的,松弛問題SILP1的最優解中員工數量不會少于M.若M個員工可生成松弛問題SILP1的一個可行解,則結論成立.具體分析如下. 不失一般性,假設問題ILP1的下界M在第1周取得.考慮下列4種所有可能的情況:i)M=A1; ii)M=1+A2+A3+A4/3;iii)M=B1d,這里d ∈D1和iv)M=[2A1+(B1,1+···+B1,5)]/5. i)當M=A1時 該情況下,可安排所有M個員工在本周雙休日當班; 而在其它3周雙休日分別安排M ?A2,M ?A3和M ?A4個員工休班.于是,所有員工在4周雙休日休班的次數為(M ?A2)+(M ?A3)+(M ?A4)=3M ?(A2+A3+A4).由引理1可知,M(A1+A2+A3+A4)/3,注意到M=A1,則有A2+A3+A42M.于是,有(M ?A2)+(M ?A3)+(M ?A4)M.該式意味著能夠保證M個員工每人在4周內至少有1 個雙休日休班. 由引理2可知,M(2A1+B1,1+···+B1,5)/5.注意到M=A1,于是,有B1,1+···+B1,53M.該情況下,考慮到員工均在本周雙休日當班,則本周5個工作日中需要安排2M個休班日期.由于周內工作日需要當班班次總數為B1,1+···+B1,5,而5M ?(B1,1+···+B1,5)2M,于是,M個員工每人可在工作日安排至少2天休班.另一方面,安排2M個休班日期之后,員工在周內工作日仍可當值3M個班次.由于本周人力需求B1,1+···+B1,53M,故總可以滿足周內工作日人力需求.所以,該情況下M個員工可生成本周內可行解方案. ii)當M=(A1+A2+A3+A4)/3時 該情況下,4周雙休日可安排休班員工數依次為M ?A1,M ?A2,M ?A3和M ?A4.于是,在雙休日休班的員工總數為4M?(A1+A2+A3+A4).考慮到A1+A2+A3+A43M,則4M?(A1+A2+A3+A4)M.該式意味著能夠保證M個員工每人至少有1個雙休日休班. 該情況下,本周5個工作日中需要安排2A1個休班日期.由引理2可知,M(2A1+B1,1+···+B1,5)/5,即5M ?(B1,1+···+B1,5)2A1成立.該式意味著本周5個工作日內可安排另外2A1個日期休班.另一方面,安排2A1個休班日期之后,員工在周內工作日仍可當值5M ?2A1個班次.由于本周人力需求B1,1+···+B1,55M ?2A1,故總可滿足本周內工作日人力需求.所以,M個員工可生成本周內可行解方案. 針對情況iii)和iv),通過與情況ii)相似分析,可以說,M個員工能夠生成松弛問題SILP1本周內的可行解方案.對于第2周、第3周或第4周,通過與第1 周情況相似分析,可以斷定M個員工能夠生成該周內可行解方案.于是,結論成立.證畢. 由引理1和引理2可知,問題ILP1最優解方案至少需要M個坐席人員.由定理2可以推斷,若在用工制度S4約束下,M個坐席人員也能生成問題ILP1可行解,則得到其最優解方案.一般情況下用工制度規定S4可能導致問題ILP1需要更多坐席人力. 定理2保證M個坐席人員可生成松弛問題SILP1最優解.不難找出1個問題實例,使得M個坐席人員是問題ILP1的最優解;也就是說,問題ILP1的下界M是最大下界.在問題ILP1 最優解中,有的坐席人員可能不止1個雙休日休班.在算法設計中,如果能夠合理利用最大下界M,則可以有效避免雙休日休班過量指派.M個坐席人員排班需要同時考慮用工制度約束S2和S4;而其它坐席人員均可安排在雙休日休班,在工作日當班只要滿足約束S4即可. 基于上節分析,啟發式算法可采用結構分解技巧.一是基于松弛問題SILP1最優解是問題ILP1最大下界,可把候選坐席人員列表從數量上分為一定或僅可能屬于最優解兩部分;針對兩類坐席人員采用不同指派策略.二是把表征人力需要的待指派班次分為屬于雙休日或工作日兩部分,分別采用不同指派策略.在工作日班次指派中,無論當班日期或班次選擇都進行局部優化和體現貪婪搜索思想.提出的啟發式算法描述如下. 啟發式算法H 步驟1由模型ILP2分別計算問題下界Aw和Bwd;并由引理1和引理2確定最大下界M.設定坐席人員列表集E1={1,2,...,M}. 步驟2對E1中員工進行雙休日班次指派.對w= 1,2,3,4,設mw=M ?Aw和ˉmw= ˉmw?1+mw,這里=0.對w=1,2,3,4,依次進行下列操作: 2–1 設k0=0和b0=0.確定kw和bw,使得ˉmw=kwM+bw成立,這里0bw 2–2 在模型ILP2分別求出的周六和周日最優解中,針對個相同當班班次(即滿足x?w6es=x?w7es=1)需求,把E1中未安排休班的個員工指派到這些雙休日班次當班. 2–3 對Aw6?個其它當班班次,把E1中尚未指派的Aw6?個員工指派到周六這些班次當班;對Aw7?個其它當班班次,把E1中尚未指派的Aw7??個員工指派到周日這些班次當班. 2–4 若Aw6 步驟3對w=1,2,3,4,把E1分為E′w={iw,1,iw,2,...,iw,M?Aw}和E′′w={iw,M?Aw+1,iw,M?Aw+2,...,iw,M}兩個子集,其中,E′w中員工在本周雙休日休班,而E′′w中員工雙休日當班.設Uw=(rwdt)5×ˉt為周w工作日區段人力需求矩陣;對工作日d=1,2,...,5,設Uwd=(rwd1,rwd2,...,rwdˉt)T為周w日期d的區段人力需求向量. 步驟4對w=1,2,3,4,就E′w和E′′w中員工工作日進行班次指派.對員工e=iw,1,iw,2,...,iw,M?Aw和員工e=iw,M?Aw+1,iw,M?Aw+2,...,iw,M,依次進行下列操作: 4–1 在Uw中選擇區段(d′,t′),使得rwd′t′=max{rwdt|t ∈T,d=1,2,...,5}成立;若有多個t′使得rwd′t′相同,則選擇使集{rwdt′|d=1,2,...,5}含正整數元素最多的區段(d′,t′); 4–2 若e ∈E′w,則令當班日期集D′w=Dw{6,7},轉入步驟4–3;若e ∈E′′w,則確定當班日期集如下: 4–3 設?S={si|si ∈S,asit′=1}和={rwdt1,rwdt2,...,rwdtc}表示由Uwd中c個最大值組成的子集.對每個si ∈和d ∈D′w,定義指標ζw(si,d)={rwdt|asit=1,rwdt ∈,rwdt >0}為班次si覆蓋中非零元素的子集. 4–5 對所有d ∈D′w和班次覆蓋區段t,如果rwdt >0,則令rwdt ←rwdt?1;使用新rwdt更新替換Uw和Uwd中相應位置元素. 4–6 當Uw >0時,區分以下情況:i)若e=iw,k且k 當Uw=0時,則令E′w和E′′w中e之后的所有員工在本周工作日休班;若存在下個周w使得Uw>0成立,則令e ←iw+1,1,轉入步驟4–1;否則,則由E1中坐席人員已生成解方案,結束. 步驟5設e=M+1和E2={e},進行下列操作: 5–1 對所有的Uw1,...,Uwh >0,安排員工e在這些周的雙休日休班,并通過與步驟4–1至步驟4–5 相似的操作,把員工e指派到這些周工作日當班;同時,對其它滿足Uw=0 的周,安排員工e該周內休班. 5–2 若存在至少1個周使得Uw >0成立,則令e ←e+1和E2=E2∪{e},轉向步驟5–1;否則,則由E1∪E2中坐席人員已生成解方案,結束. 在假設工作區段數ˉt和班次數ˉs給定情況下,排班問題規模可用人力需求輸入參數 來刻畫.容易看出,步驟4的每個員工指派過程中,至少存在1個周,使得該周工作日當班班次至少覆蓋1個區段的有效人力需求(即指派后該區段剩余人力需求滿足rwdt ?10);另一方面,每個員工4 周內當班/休班指派的計算時間不會超過O(max{4×52×,4×5×ˉs}),其中大括號內前項計算確定員工當班日期(步驟4–1 和步驟4–2),而后項確定當班班次(步驟4–3和步驟4–4).考慮到ˉt和ˉs是問題常數,所以說,步驟4 的計算時間為O(rsum).相似分析可推斷步驟5的計算時間也不超過O(rsum).另外,其它步驟2和步驟3計算時間并不占優.因此,在步驟1 使用模型ILP2求出最大下界M之后,算法H中步驟2 至步驟5 的計算時間復雜度為O(rsum). 在算法H中,步驟2在每個周w雙休日總是指派Aw個坐席人員當班.無論周六或周日需要當班員工數不會超過Aw,因此,生成解能夠滿足雙休日人力需求.在每個周w的工作日,步驟4至步驟5依次把坐席人員指派到具體班次當班,直至周內工作日區段人力需求Uw= (rwdt)5×ˉt被滿足.所以,生成解也能滿足工作日人力需求. 由引理1和引理2可知,問題最少需要M個坐席人員在4周計劃周期內當班.從步驟2至步驟4 可以看出,對集E′w中M個坐席人員,每周有M ?Aw個人至少在雙休日休班,而Aw個人至少在工作日休班2天.若生成解中還有另外|E2|個坐席人員當班,由步驟5可知,這|E2|個坐席人員至少會在周內雙休日休班.所以,生成解能夠滿足用工制度約束S1. 在步驟2的2–1中,每周指派M ?Aw個不同坐席人員雙休日休班,4周共指派4M ?(A1+A2+A3+A4)個雙休班.由引理1 的2)可知,4M ?(A1+A2+A3+A4)M.進一步分析步驟2–1可知:指派始于第1周的情況i)k1=k0= 0,對所有情況i)ki=ki?1= 0 指派后,必然出現情況iii)kw=kw?1+1 = 1的指派.當該情況出現時,由于=M+bw=+mwM和< M,則bwmw.于是,在該情況下對坐席人員Aw+1,Aw+2,...,M的休班指派必然覆蓋坐席人員bw?1+1,bw?1+2,...,M.因此,考慮到所有ki=ki?1= 0情況已對坐席人員1,2,...,bw雙休日休班進行指派,情況iii)休班指派之后,已經可保證集E1的M個坐席人員均在雙休日至少休班1次.對于生成解中其它坐席人員,步驟5均指派他們在每周雙休日休班.因此,生成解能夠滿足用工制度約束S2.另外,從步驟4至步驟5容易看出,生成解也滿足用工制度S3和S4.總結以上分析,有以下結論. 定理3啟發式算法H生成問題ILP1的可行排班方案. 由定理2和定理3可知,若算法H結束于步驟4,則生成解是最優排班方案.由于用工制度規定S4可能致使需要更多坐席人力配置,步驟5通過采用類似步驟4 的局部優化策略來補充配置更多坐席人力. 某呼叫中心企業承包若干制造商電子產品售后電話服務業務.企業把坐席人員分為若干服務群組,每個服務群組由十幾到幾十個坐席人員不等組成,提供由相近產品組成的產品線話務服務支持.坐席人員的當班班種班次設置見表2.假設日內區段時長為1 h,根據區段電話實際呼入量以及承包合同指標TSF要求,使用該群組坐席服務時間統計量,采用Erlang A方法可計算出所有區段坐席人力需求數量rwdt;該參數用來表示排班服務指標TSF要求.計算使用臺式計算機的CPU為Intel 酷睿i7四核處理器,主頻為2.8GHz.計算實驗采用CPLEX 12.1求解整數規劃模型;使用C++編程實現啟發式算法H. 表2 某呼叫中心的班種班次列表Table 2 List of shift-types and shifts in a call center 下面通過問題實例,說明啟發式算法H的計算過程及結果. 1)區段人力需求計算 呼叫中心服務群組工作時間如表2中班次覆蓋的15個區段,依次分別用符號t1,t2,...,t15來表示.企業承包制造商服務合同的指標TSF 要求取值85%.根據該群組最近半年(26周)實際數據樣本,通過檢驗擬合分析,確定坐席人員服務率μtd取值0.305/min,顧客耐心時間b取值3.45 min.表3列出該實例每日電話呼入統計量.由表3可看出,周內不同日期電話呼入量差異明顯,需要合適指派員工當班/休班日期來滿足不同日話務量服務需求.使用Erlang A可計算出4周所有工作區段人力需求.表4列出第2周的周一所有區段電話實際呼入量和人力需求計算結果.由表4可看出,日內不同區段電話呼入量存在波峰波谷現象,需要通過合適安排員工班次來有效應對日內人力需求變化. 表3 問題實例每日電話呼入統計量Table 3 Daily inbound calls of the problem instance 表4 某日內區段呼入量和計算的人力需求分布Table 4 Inbound calls of intervals and calculated labor demands one day 2)員工雙休日指派情況 算法H中,步驟1通過模型ILP2計算的(A1,A2,A3,A4)=(6,6,7,7),計算的所有Bwd依次列表為(8,7,7,8,7; 9,9,8,8,8; 8,8,7,8,7; 9,7,9,9,8).由引理1和引理2計算出M=12.步驟2通過對M個坐席人員4個周末當班/休班指派,一方面保證滿足每個雙休日人力需求,另一方面保證每個坐席人員至少1個雙休日休班.由于M個坐席人員尚未覆蓋4周所有工作日人力需求,需要通過步驟5 指派坐席人員e13在一些工作日當班.該情況下,坐席人員e13在4個雙休日休班.坐席人員雙休日當班/休班情況見表5. 表5 坐席人員雙休日當班/休班情況Table 5 Attendance of agents on weekends 3)員工工作日指派情況 算法H中,步驟4對坐席人員e1至e12的每周工作日進行休班或當班班次指派.步驟4的班次指派,都是挑選覆蓋周內工作日區段人力需求最多的班次,體現了局部貪婪優化思想.步驟5指派坐席人員e13在第4周工作日當班情況為s11{1,3,4,5},其它周工作日均休班.所有坐席人員工作日當班/休班情況見表6.表中符號,如s3,表示坐席人員周內所有工作日班次s3當班;s2{4,5}表示坐席人員在周內周四和周五休班,其它工作日班次s2當班;“—”表示坐席人員周內所有工作日休班. 表6 坐席人員周內工作日當班/休班情況Table 6 Attendance of agents on weekdays 5.2.1 性能評估 從呼叫中心小規模服務群組選擇10個問題實例,分別使用ILP1模型和啟發式算法H求解排班問題,記錄了算法計算時間(s)和計算出的坐席人員數量.這里假設若在1小時內尚未得到最優解,則認為模型ILP1無法獲得最優解.具體計算結果見表7. 根據表7,從計算成本與優化性能兩方面,對模型和算法分析如下,①模型ILP1 對10個實例的平均計算時間為1 916.5 s,其中2個實例在3 600 s 內未能獲得最優解.這表明該排班問題本質上是非常復雜組合優化問題.模型ILP1盡管理論上說可求得問題最優解,但由于其計算成本過大,只適合求解小規模問題.②啟發式算法H對10個實例的平均計算時間為35.6 s,遠小于模型ILP1的計算成本.這表明該算法具有良好的計算性能.③從優化性能上看,算法H 發現10個實例中的5個最優解,其它實例情況只與最優解(或下界)多1人.這表明算法H無論逐步分解結構,或者班次覆蓋區段人力需求特征指標刻畫以及局部優化員工指派,能夠充分反映該排班問題內在優化規律.算法H能夠獲得小規模問題實例的最優解或次優解. 表7 小規模問題實例計算結果Table 7 Experimental results of the small-scale problem instances 從較大規模服務群組選擇了10個問題實例.由于無法在合理計算時間(1小時內)使用模型ILP1獲得問題最優解,通過下界來評估啟發式算法H的性能.定義算法H 的性能誤差率=(算法H的解評估下界M)/評估下界M.計算結果見表8. 根據表8,對算法H進一步分析如下,①盡管在理論上很難給出步驟1中模型ILP2 求下界M的計算時間復雜度,但如節4中分析所示,步驟2至步驟5的計算時間成本O(rsum)是隨著問題規模而線性增長的.對于10個較大規模問題實例,模型ILP1在1小時內無法獲得最優解;但算法H的平均計算時間僅為61.4 s.另外,與表7對照可以看出,算法H隨著問題規模變大其計算時間增長并不很大.據此可說,算法H能夠用來求解大規模排班問題.②從優化性能來看,算法H與評估下界M比較,平均性能誤差率不超過5.8%.注意到下界M可能小于最優解(參照表7),表中所示誤差率可能低估了算法H的優化性能.據此可說,算法H能夠發現大規模排班問題優化解. 表8 較大規模問題實例計算結果Table 8 Experimental results of the large-scale problem instances 5.2.2 問題討論 排班問題中,用工制度規定S2+S3體現了坐席人員雙休日休班公平性; 規定S4 保證坐席人員周內工作日當值相同班次.這些排班規定體現企業人性化管理理念.通過是否保留模型ILP1中描述用工制度規定S2+S3及S4的約束條件式,或者使用算法H(適當修改),可計算討論這些規定因素對排班人力成本控制的影響.計算結果見表9. 表9 用工制度規定對人力成本影響計算結果Table 9 Experimental results about the influence of labor restrictions on human cost ①從表9可看出,無論考慮保證每個員工至少1個雙休日休班,或者保證每個員工每個周內工作日同班次當班,都有可能增加排班用工成本.如果同時考慮兩者,用工成本增加可能會更多.表中用工成本最小增長率為0%,意味著針對該實例,借助優化模型算法可實現成本最優,同時兼顧員工雙休日休班公平性和保證周內工作日上班規律性. ②保證員工周內工作日上班規律性(S4)比保證員工雙休日休班公平性(S2+S3)可能需要更多人力成本.從呼叫中心話務呼入量分布不難看出,一方面,周末呼入量通常比工作日偏少(如見表3),這給員工雙休日休班提供了較多機會;只要借助優化模型算法,可較好實現人力成本控制和保證周末休班公平性雙重目標.另一方面,周內不同工作日呼入量分布具有不均衡性,同班次規定某種程度上限制了不同工作日人力匹配靈活性,從而引起人力成本上升. ③從表9可看出,呼叫中心業務規模越小,周末休班公平性和同班次用工制度引起的人力成本增加越大.這意味著小規模呼叫中心企業面臨著突出的用工成本控制與人性化管理兩難問題.當呼叫中心企業規模較大時,人力成本與人性化管理比較容易平衡. 針對呼叫中心企業管理實際需求,研究納入周末休班公平性和周內工作日同班次約束的多周排班優化問題.通過分析認識問題結構及優化規律,構建問題整數規劃模型和提出構造性啟發式算法.計算實驗表明規劃模型適合求解小規模排班問題最優解,而啟發式算法能夠以小計算成本獲得較大規模排班問題優化解.研究結果表明在排班問題中納入諸如員工訴求及人性化管理因素,盡管對企業長期發展有利,但也可能導致人力成本稍許增加.考慮諸多用工實踐情景的坐席人員排班問題,本質上通常是非常復雜的組合優化問題,給學術界提供很多研究機會.3.2 優化性質
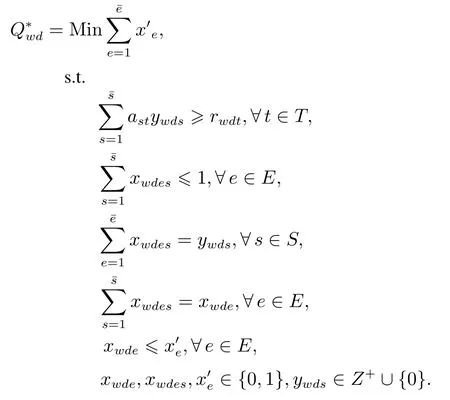
4 啟發式算法

5 計算實驗
5.1 實例計算
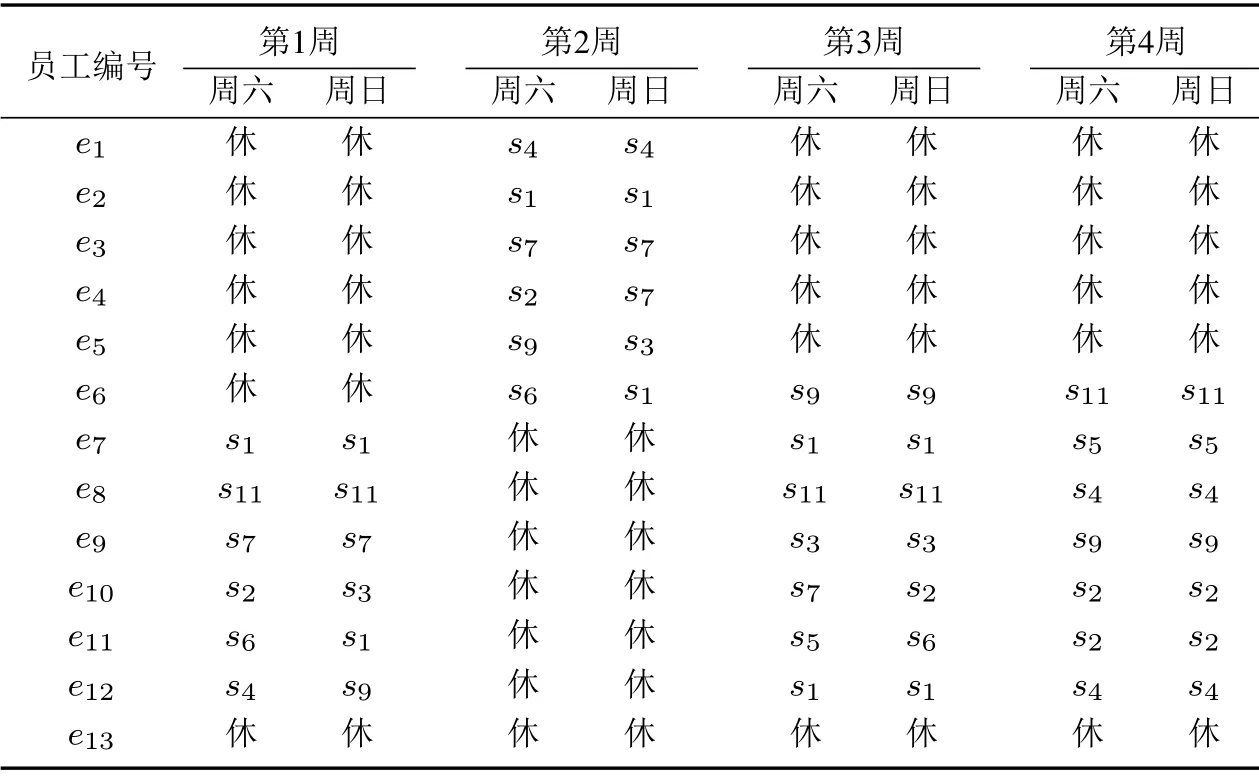
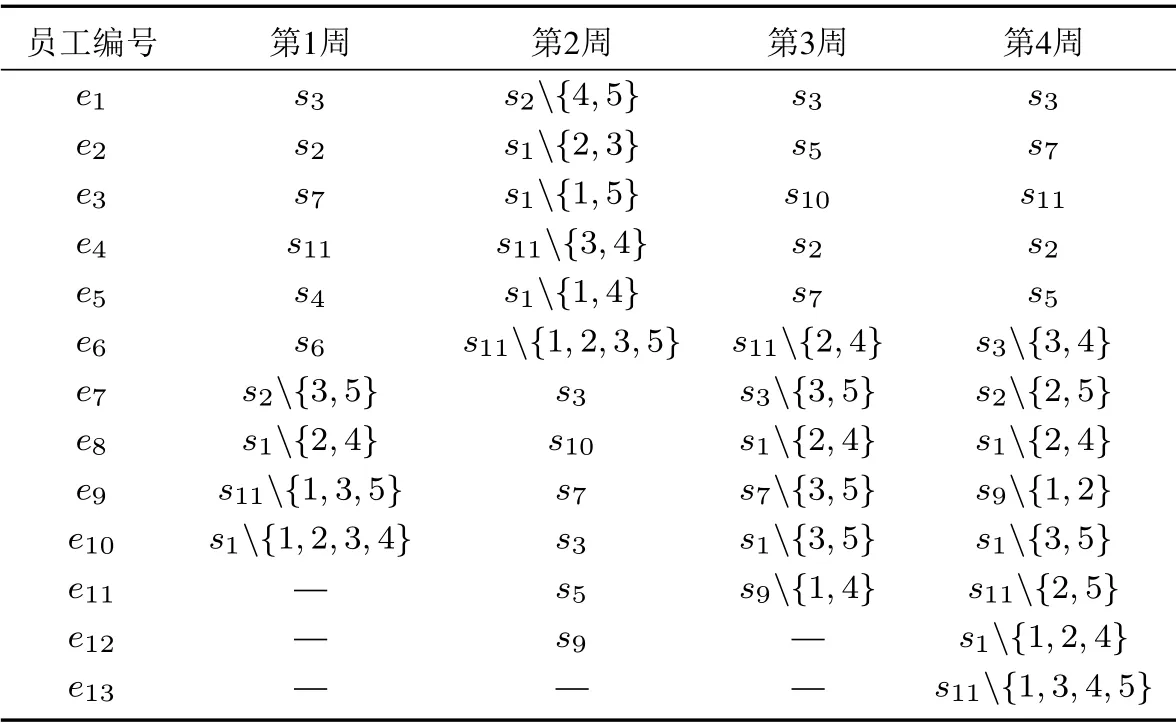
5.2 實驗分析

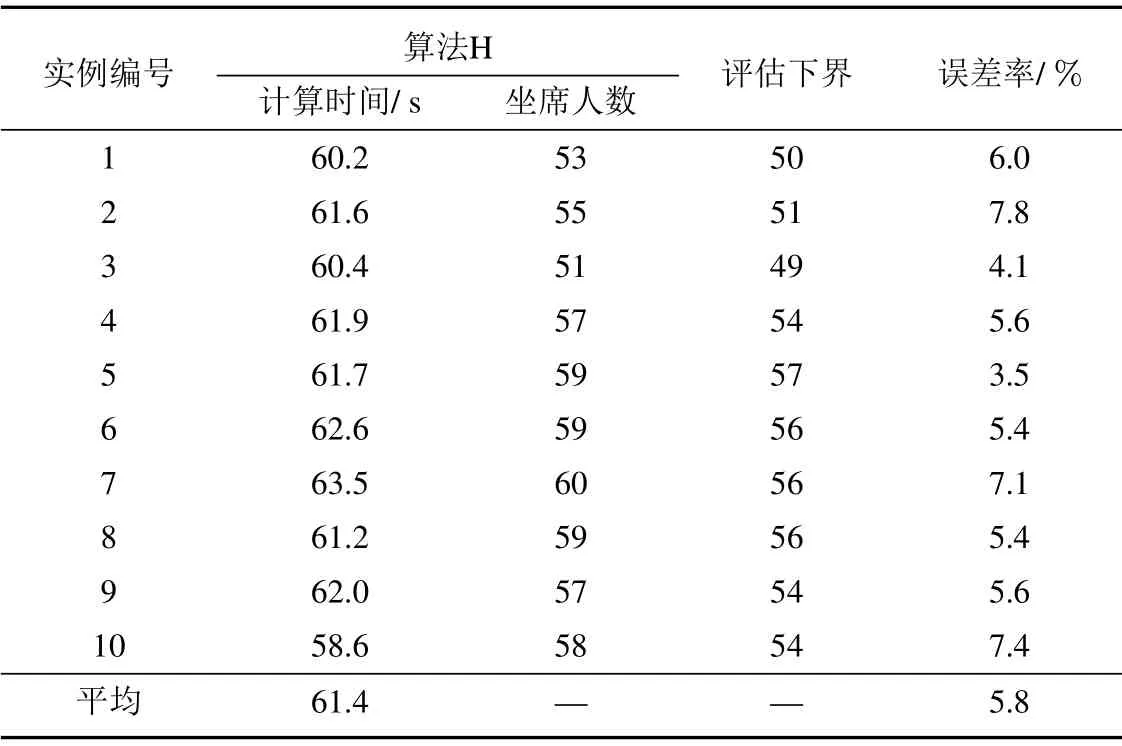
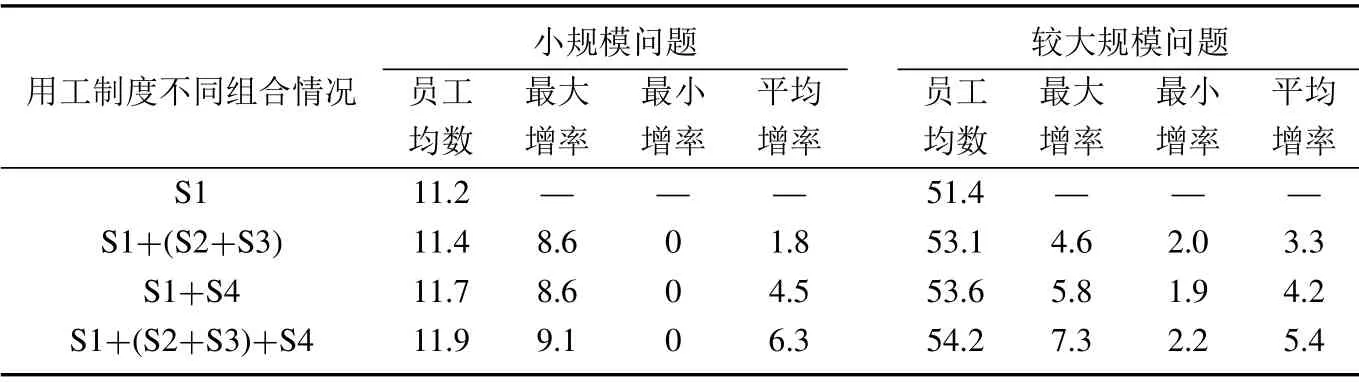
6 結束語

