從選考試題看對分查找算法問題的 解題策略

傅琳璐

對分查找算法作為程序設計中的經典算法之一，是一種高效的查找方法。縱觀浙江省2015—2020年的信息技術選考試題，可發現對分查找算法是每年選考試題中的必考內容。從最開始簡單的查找區間計算，到算法思想應用……再到今年的對分查找變形程序分析，試題考查內容的角度在變，難度也在逐步增大。這就要求學生在平時的學習過程中不僅要深入理解對分查找算法思想，建立良好的算法思維和計算思維，還要掌握一定的解題策略，具備良好的解題能力，只有這樣才能在選考考試中做到“倉里有糧，心中不慌”。

● 勤用列表追蹤查找過程

例1.（2017.4選考真題）某對分查找算法的VB程序段如圖1所示。數組元素a（1）到a（10）的值依次為“8，17，24，30，36，40，55，58，61，66”，文本框Text1中輸入的值是30，執行該程序段，文本框Text2中顯示的是（? ）。

A.40 24? ?B.40 24 36

C.36 24? ?D.36 17 24

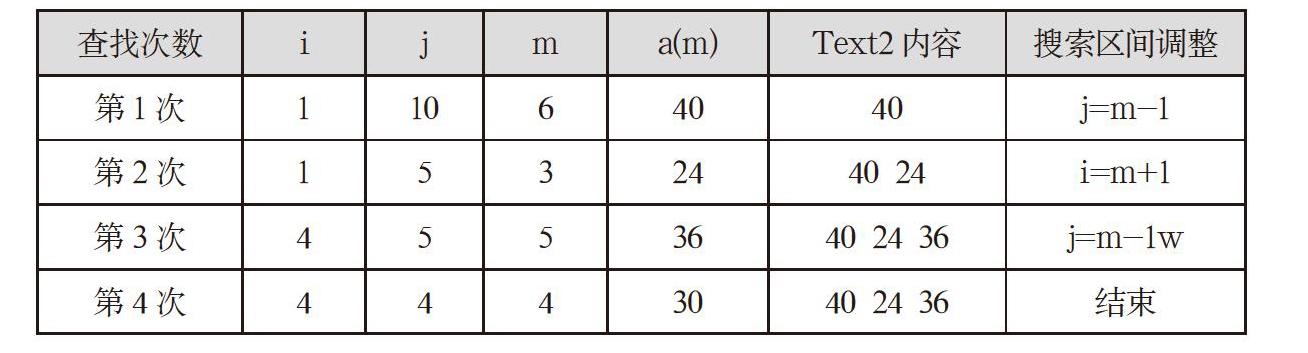
剖析：此題為對分查找過程分析題，查找鍵key值已知，所求文本框Text2中顯示的內容為對分查找過程中找到key值之前依次訪問到的數據a（m），解題時可用列表法記錄對分查找過程中各個變量值的變化（如下表）。

點評：列表法是解決對分查找問題最簡單有效的方法，過程清晰，一目了然。用列表法將對分查找算法執行一遍，可以清楚準確地觀察到查找過程中各個變量值的變化，同時還可以幫助學生鞏固算法過程，加深對算法思想的理解，答題正確率高，非常適合算法的初學者。但是列表法比較費時，在遇到對分查找次數較多或查找鍵key值未知，查找過程不唯一的問題時，解題效率不高。

● 活用特征判斷程序結果

例2.（2017.11選考真題）某對分查找算法的VB程序段如下頁圖2所示，數組元素a（1）到a（7）的值依次為“24，35，38，41，45，69，78”。若該程序段執行后，文本框Text1中顯示的內容可能是（? ?）。

A.RL? ? B.LMR

C.RLR? ? D.LRLM

剖析：此題為對分查找過程分析題，key值未知，查找過程不唯一，不適用列表法求解，但分析題目發現本題可直接運用對分查找的特征結論來排除部分選項。

特征：①無論查找鍵key是否在被查找數組中，n個數的對分查找最多查找次數為int（log2n）+1。②如果查找鍵key在被查找數組中，n個數的對分查找最少查找次數為1次;如果查找鍵key不在被查找數組中，n個數的對分查找最少查找次數為int（log2n+1）。

分析程序可知，程序有兩個結束出口：一是查找成功立即退出，字符串s以“M”結尾;二是查找不成功，字符串s中沒有“M”。因此“M”不可能在字符串s中間，排除B選項;查找不成功時，對分查找最少要查找int（log2n+1）=3次，排除A選項;n個數的對分查找次數最多查找int（log2n）+1=3次，排除D選項。

點評：用對分查找算法的特征結論可以快速準確地完成試題分析，達到事半功倍的效果，對分查找算法還有如下3個特征：①如果查找鍵key在被查找數組中，則對分查找一定可以找到key，且查找結束時變量i，j的關系一定為i≤j。②如果查找鍵key不在被查找數組中，則對分查找結束時變量i，j的關系一定為i>j，且i=j+1。③如果查找鍵key不在被查找數組中，則對分查找結束時變量i，j一定指向與key值最接近的兩個數。

● 巧用二叉樹羅列查找分支

例3.（2020.1選考真題）某對分查找算法的VB程序段如圖3所示。數組元素a（1）到a（10）的值依次為“2，3，5，8，9，10，13，17，19，20”。在文本框Text1中輸入待查找的數，執行該程序段，則文本框Text2中顯示的內容可能是（? ?）。

A. 9? 3

B. 9? 3? 5

C. 9? 17? 19? 13

D. 9? 3? 5? 8? 19

剖析：此題為對分查找變形程序，查找成功時沒有立即結束，一直進行到沒有可查找區間（i>j）時結束，查找次數多。且查找鍵key值未知，查找過程不唯一，查找分支多，不適合用列表法解題。但只要畫出二叉樹模擬所有查找分支，就可快速解出此題，明確只有B選項符合。

點評：二叉樹作為一種特殊的樹形結構，是計算機科學領域中一種重要的數據結構。二叉樹的樹形結構剛好可以模擬出對分查找過程中依次訪問到的中間位置元素，直觀形象、條理清晰。所以，當遇到查找鍵key值未知，查找過程不唯一，需要考慮所有查找分支的試題時，用二叉樹求解尤為方便快捷，解題效率會比列表法高。

● 善用數軸分析算法思路

例4.（2018.4選考真題）數組a為一組正整數，奇數在前，偶數在后。奇數與偶數已分別按升序排序。依據對分查找思想，設計一個在數組a中查找數據Key的程序。實現該功能的VB程序段如圖4所示。程序中方框處可選語句為：①i=m+1，②j=m-1，③If Key

A.①、②、③? ? B.①、③、②

C.②、①、③? ? D.③、②、①

剖析：此題為對分查找算法在特殊數列中的應用。因為被查找數據是前奇后偶的兩個升序段，且查找鍵key值未知，所以不能直接用標準對分查找程序進行對分查找，需要根據數據的特點分情況討論來調整下一次的查找區間，本題可分三種情況來討論分析：

情況1：如果查找鍵key為奇數，中間位置元素a（m）為偶數[Key Mod 2=1 And a（m） Mod 2=0]。因為奇數在前偶數在后，所以應調整下一次的查找區間為前半部分，即修改變量值j=m-1。

情況2：如果查找鍵key為偶數，中間位置元素a（m）為奇數[Key Mod 2=0 And a（m） Mod 2=1]。因為奇數在前偶數在后，所以調整下一次的查找區間為后半部分，即修改變量值i=m+1。

情況3：如果查找鍵key與中間位置元素a（m）的奇偶性一致，那么根據key值與a（m）的大小關系調整下一次的查找搜索區間。

點評：對分查找在特殊數列上應用的試題，強調考查學生的算法思維和算法分析能力，而算法分析正是教學中的重點也是難點內容。在算法分析過程中如果可以先使用圖表畫出數據特點，化抽象為具體，則可以使程序變得形象化、具體化。

本文以近幾年選考卷中的對分查找算法試題為例，總結提出了4種針對對分查找算法問題的解題策略，并分析了不同解題策略所適用的試題題型。希望學生們在面對對分查找類試題時，可以靈活運用各種解題策略，迅速找到最合適的解題方法，準確高效地解出題目。但是試題千變萬化，高中信息技術一線教師在平時的算法教學中，除了要讓學生掌握解題策略，提高解題能力之外，更重要的是要讓學生理解算法思想，建立算法思維，提高算法閱讀能力和分析能力，培養計算思維能力，將信息技術學科的核心素養培養落到實處。