一種兩階段變量選擇的LIBS定量分析方法
郭宇瀟,史晉芳,王慧麗,邱 榮,鄧承付
(1.西南科技大學制造科學與工程學院 教育部制造過程測試技術重點實驗室,四川 綿陽621010; 2.西南科技大學 極端條件物質特性聯合實驗室,四川 綿陽 621010)
1 引 言
激光誘導擊穿光譜是一種原子發射光譜技術,在分析物質成分方面有很大潛力。LIBS定量分析一直是一個研究難題[1],已有研究表明,機器學習方法能顯著提升LIBS定量分析效果,例如支持向量回歸(Support Vector Regression,SVR)[2-3]、人工神經網絡(Artificial Neural Network,ANN)[4-5]、隨機森林(Random Forest,RF)[6-7]、偏最小二乘回歸(Partial Least Squares Regression,PLSR)[8-9]、最小絕對收斂選擇算子(Latest absolute shrink and selection operator,Lasso)[10]等。然而,如何從數以萬計的光譜信息中提取有效信息,進行高效的變量選擇,是建立高質量定量分析模型的關鍵[11]。
LIBS定量分析的變量選擇方法可以分為兩類:(1)基于先驗知識的手動變量選擇[12];(2)基于機器學習中優化方法的自動變量選擇[13]。前者需要一些基體的知識,所選的變量往往包含基體元素的發射線。例如,Sirven[14]在使用LIBS結合ANN分析土壤中Cr的含量時,同時選擇了目標元素Cr和基體元素Fe的發射線作為ANN的輸入變量。然而,在大部分場景(例如:土壤)先驗知識往往難以獲得。目前,研究者更致力于探索基于機器學習方法的變量選擇。Guezenoc[11]使用LIBS定量分析土壤中的K,采用經典的PLS-VIP進行變量選擇,最終建立并比較了3種PLS模型,不過,作者在研究中仍然手動排除了H、Ca的發射線和608~1000 nm波長范圍的變量。除此之外,連續投影算法(Successive Projection Algorithm,SPA)[15]、遺傳算法(Genetic Algorithm,GA)[16]在LIBS分析中也有應用,但是這些方法的計算量都非常龐大。Duan[15]使用LIBS定量分析土壤中的Cu、Ba、Cr,分別以SPA和GA作為變量選擇方法,計算時間分別為7200 s和1200 s。Yan[17]在使用LIBS定量分析煤炭的熱值時,提出一種小波變化(Wavelet Transformation,WT)結合平均影響值(Mean Influence Value,MIV)的變量選擇方法并取得了較好的結果,不過MIV閾值的不當選擇可能導致丟失重要信息。
針對LIBS定量分析的變量選擇問題,提出一種結合排序和搜索策略的兩階段變量選擇方法,該方法無需先驗知識,能自動、快速完成變量選擇。將之結合不同機器學習方法,提升LIBS定量分析的精密度和準確度。
2 LIBS實驗
2.1 樣品制備
LIBS實驗以標準土壤樣品GBW07387(GSS-31)作為分析物。首先,將10份純凈的、不同質量的(C2H3O2)2Sr混合PE微粉(HDPE,1810)和標準土壤,在瑪瑙研缽中均勻研磨,得到10個Sr濃度在110~850 ppm之間的土壤樣品。然后,每個樣品在20 MPa壓力下壓成薄片(φ12 mm×2.3 mm)。
如表1所示,根據濃度從高到低,將樣品標記為C1~C10。C2和C9作為驗證集,其他樣品作為定標集。
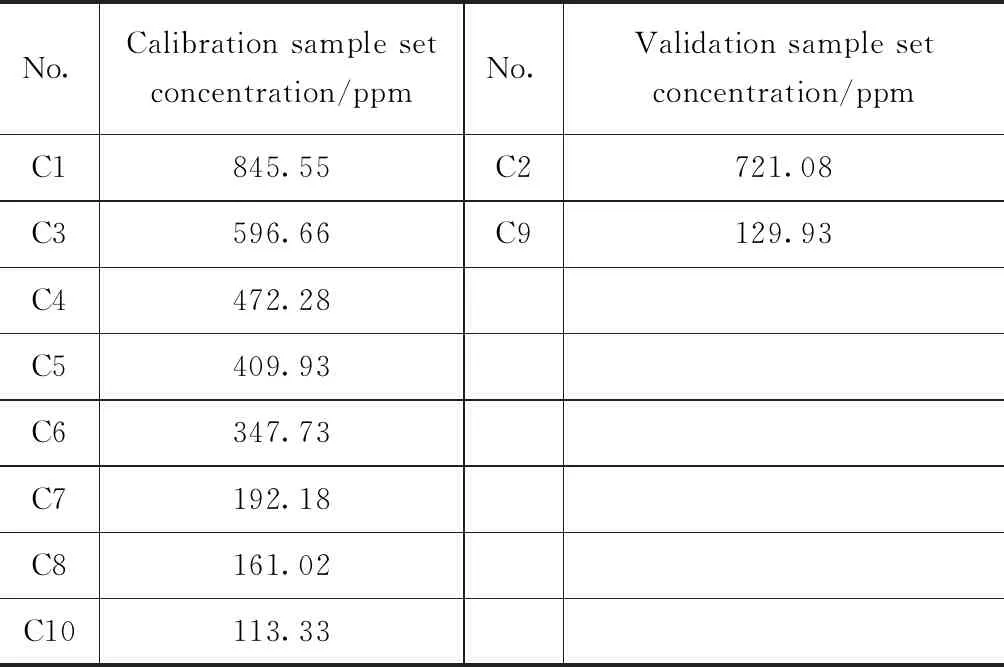
表1 樣品分類
2.2 數據采集
LIBS設備如圖1所示。光源為兩個調Q Nd-YAG激光器(λ1=355 nm,λ2=1064 nm)。激光器1(Spectral Physics,LAB-190-10)能量為45 mJ,脈沖持續時間10 ns。激光器2(Innolas,Spitlight 600)能量45 mJ,脈沖持續時間7 ns。樣品置于X-Y-Z平臺(LTB,XYZ-Tish)。兩道激光光束通過透鏡(focal length=300 mm)匯聚于樣品表面2 mm以下。等離子體輻射由透鏡(focal length=150mm)聚焦,由光纖采集,用光譜儀(LTB,Aryelle200)進行分析。光譜儀的光譜間隔在193~793 nm之間,分辨率為0.02 nm。延遲由延遲生成器(DG645,stanford)生成。優化實驗參數后,將兩個激光器的延遲固定為1 μs,將光譜儀采集延遲設定為第二次激光脈沖后3.3 μs,ICCD(Andor,i-star)積分時間為1 s。
在每個樣品的表面5×5矩形方陣上一共采集25幅光譜,除去離群值后,10個樣品一共獲得220幅光譜。由于每一幅光譜有42870個波長,即42870個強度值,可以得到一個光譜矩陣X[220,42870]和標簽矩陣y[220,1]。
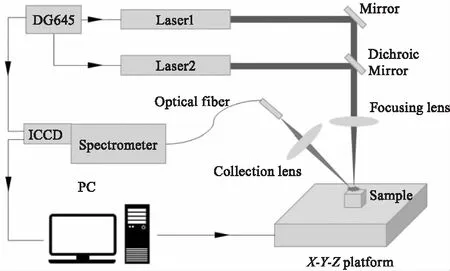
圖1 LIBS原理
3 變量選擇方法
在實際測量的光譜中,由LIBS實驗得到的光譜矩陣為X[m,n],待測元素濃度矩陣為y[m,1],其中,m為光譜數量,n為一幅光譜擁有的強度值數量。一幅LIBS光譜由大量波長對應不同的強度值構成,一幅光譜可以記為[x1,x2,…,xn]。大多數情況下,待測元素原子發射光譜譜線強度值x與待測元素的濃度y符合塞伯-羅馬金(Schiebe-Lomakin)公式:
x=a·yb
(1)
式中,a、b在一定條件下為常數,常數b與譜線的自吸收有關,當譜線自吸收可以被忽略時b=1,此時元素的發射線強度x與該元素的濃度y呈線性關系。
3.1 基于皮爾遜相關系數的排序策略
皮爾遜相關系數r是用于計算兩個變量之間線性相關性的統計準則,它可以與實驗獲得的光譜數量m構成統計量F:
首先,完善集成電路產業的風險投資機制:一方面,由國家在技術創新初期投入一定比例的種子基金,建立風險投資基金,通過風險投資機構以股份的形式向社會公開募集;另一方面,通過稅收優惠等政策,吸引國外風險投資基金尤其是跨國公司投資我國的集成電路產業。同時,政府可以設立專項資金,成立集成電路產業風險擔保基金,為一些國家戰略重點發展的技術項目提供部分的融資擔保。
(2)
其中,std( )是標準偏差;cov( )是方差。
通過計算待測元素濃度y與光譜中每個強度變量{xi|xi∈[x1,x2,…,xn]}的F,獲得集合[F1,F2,…,Fn]。變量xi的得分Fi越高,則xi與待測元素濃度y之間的線性相關性越強。通過皮爾遜相關系數可以快速得出每個強度變量xi與待測元素濃度y的相關性,變量的排序策略如圖2所示。通過變量評價準則F計算每個變量xi的得分Fi,選擇前k個得分最高的變量從而快速排除與待測元素濃度y無關、弱相關的變量,并將保留的變量記為S1,S1=[x1,x2,…,xk]。
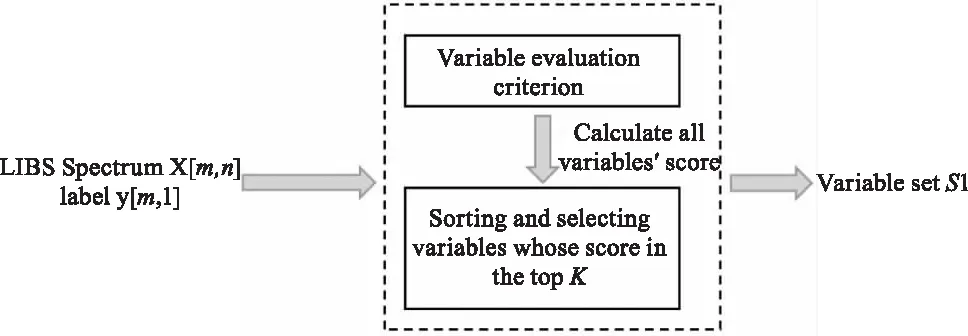
圖2 變量排序過程
3.2 基于近似馬爾科夫毯(AMB)的搜索策略
排序策略并不能消除冗余變量,變量集合S1中的冗余變量會干擾機器學習模型的準確度和精密度,本文中使用近似馬爾科夫毯消除S1中的冗余變量。
在變量集合U中,對于變量x∈U,變量集合MB∈U(x?MB),若有:
x⊥U-MB-x|MB
(4)
認為當MB存在時,x對問題沒有貢獻,可以被刪除。由于馬爾科夫毯的時間復雜度極高,實際中,近似馬爾科夫毯常被用于消除冗余變量。下列條件滿足時,變量xi是變量xj的AMB:
(5)
其中,MIC(x,y)表示變量x和變量y的最大信息系數。
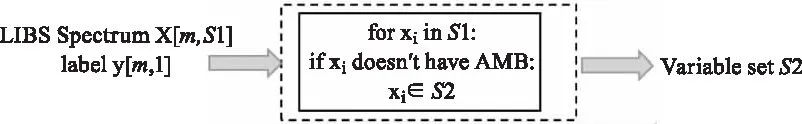
圖3 變量搜索過程
3.3 基于兩階段變量選擇的LIBS定量分析方法
基于兩階段變量選擇的LIBS定量分析流程如圖4所示。首先通過離散小波變換(Discrete Wavelet Transform,DWT)對原始LIBS光譜進行降噪和去基線,然后通過排序策略得到變量集合S1,之后通過搜索策略得到變量集合S2,最后將S2作為機器學習方法的輸入變量,得到土壤中目標元素Sr的濃度預測模型。
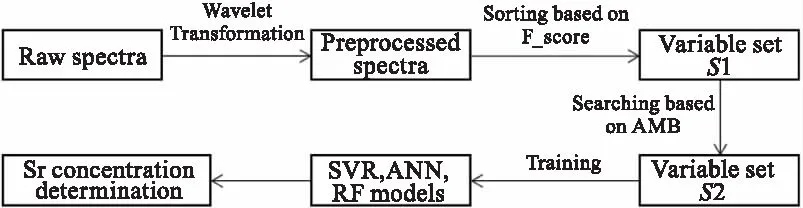
圖4 基于兩階段變量選擇的LIBS定量分析流程
4 數據處理
實驗采集的典型LIBS光譜如圖5所示,根據NIST數據集,圖中標注了Sr I 460.73 nm,小圖中的黑線代表原始光譜,紅線代表DWT對原始光譜降噪和去基線的效果。
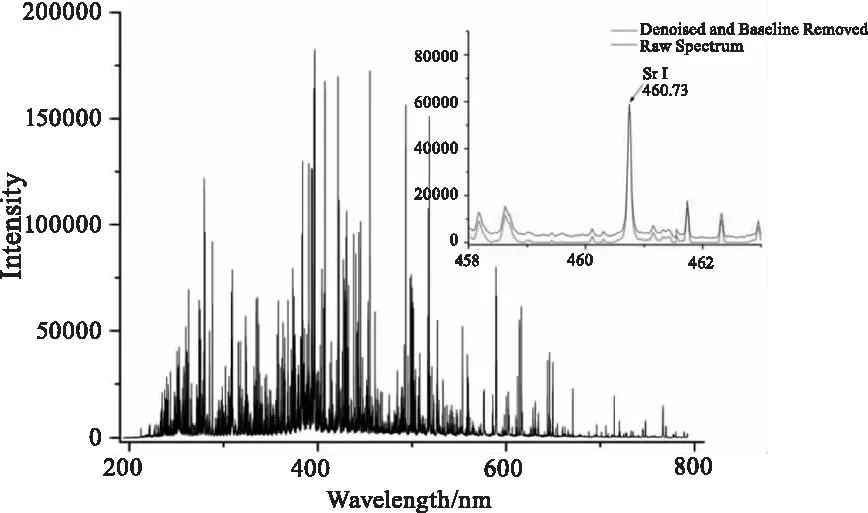
圖5 樣品C2的平均光譜
4.1 兩階段變量選擇
LIBS變量選擇由兩階段組成。在第一階段,通過排序策略從原始光譜X[220,42870]中保留178個與目標元素Sr濃度相關性最大的變量,保留的變量集合記為S1,這個階段保留的變量數目k一般參考定標集中光譜的數量[18]。在第二階段,通過搜索策略從S1篩選出14個沒有AMB的變量,保留的變量集合記為S2。與S1不同的是,第二階段保留的變量數目是唯一確定的。圖6的(a)和(b)分別顯示了S1和S2中的變量。完成變量選擇后,光譜矩陣由X[220,42870]變為X[220,14],其中的時間成本為3.75 s。
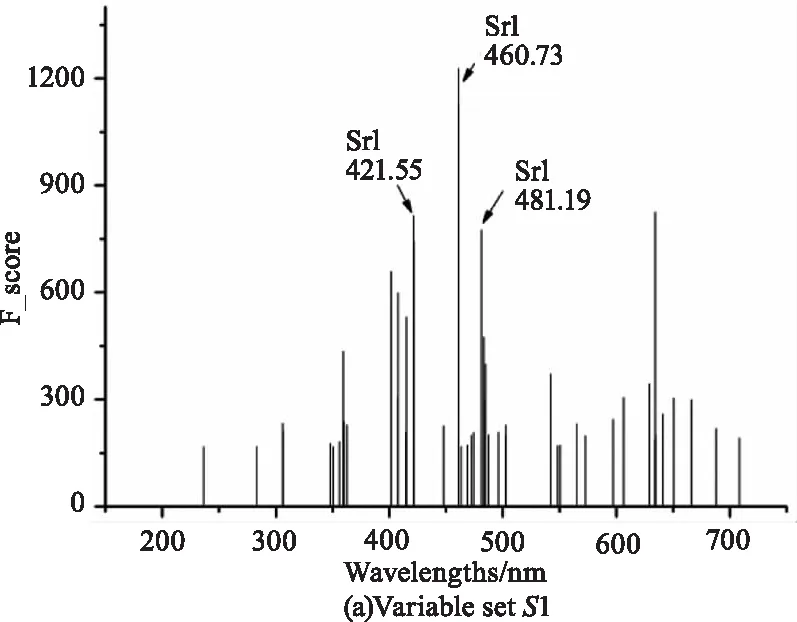
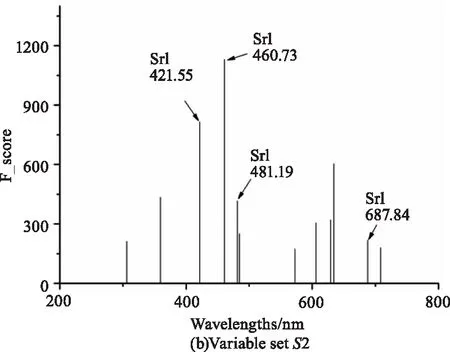
圖6 Wavelengths stored by sorting and searching strategy
4.2 LIBS定量分析模型
以變量集合S2結合SVR、ANN和RF,獲得的3種定標模型性能如表2的No.1,2,3所示,定標曲線如圖7所示。本文通過絕對系數R2、均方根誤差RMSE、相對偏差RE、相對標準偏差RSD來全面評價模型的質量。
就準確度而言,三種模型的R2均高于0.99,REC(RE of Calibration set)和REP(RE of Validation set)均低于5 %,RMSEC和RMSEP均低于22 ppm,表明三種模型都有很好的預測能力。就精密度而言,三種模型的RSD均低于20 %,說明模型對同一樣品表面不同位置的光譜預測偏差較小。
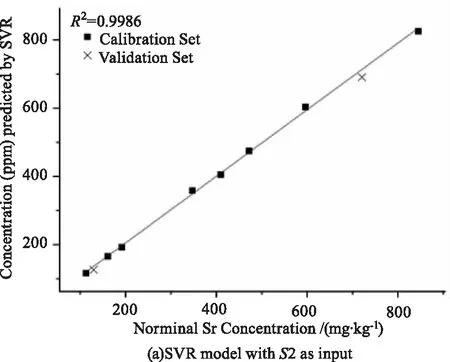
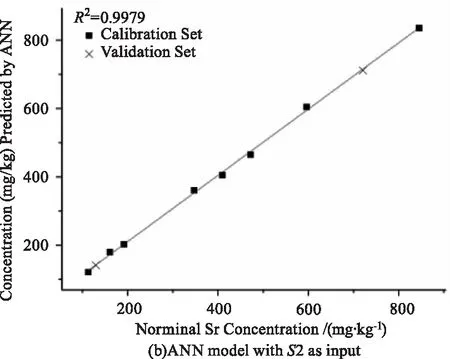
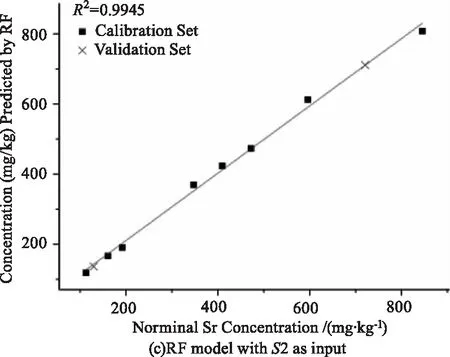
圖7 以S2為輸入變量建立的3個定標模型
將本文提出的變量選擇方法與經典的變量選擇方法PLS-VIP作比較。在實踐中,一般選擇VIP值大于1的變量作為機器學習模型的輸入變量[11]。通過PLS-VIP方法,從X[220,42870]中篩選出9994個VIP值大于1的變量,將此變量集合記為S3。完成變量選擇后,光譜矩陣由X[220,42870]變為X[220,9994]。將S3分別作為ANN、SVR和RF的輸入變量,得到的定標模型的性能如表2的No.4,5,6所示。
可以發現,無論是準確度還是精密度,以S2為輸入的3種定標模型均優于以S3為輸入的3種定標模型。
5 結 論
本文針對LIBS定量分析中的變量選擇問題,提出一種兩階段的變量選擇方法,并將該方法結合機器學習方法用于土壤中Sr的定量分析。將該方法得到的14個變量集合記為S2,將PLS-VIP方法得到的9994個變量集合記為S3。通過比較分別由S2和S3生成的ANN、SVR、RF發現:以S2生成的模型,R2大于0.99,RE低于5 %,RMSE低于22 ppm,RSD低于20 %,準確度和精密度均優于以S3生成的模型。研究結果證明了該方法的高效性和普適性,在LIBS定量分析中有著重要作用。
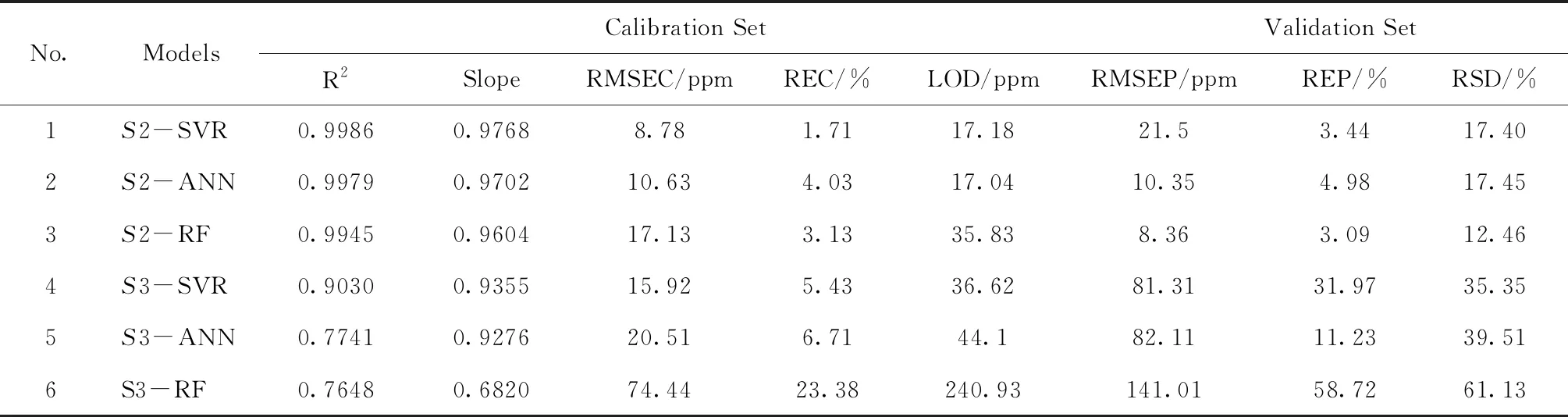
表2 分別以S2、S3為輸入的SVR、ANN、RF模型的表現

