變形L1正則化的高光譜圖像稀疏解混

李 璠,吳朝明,張紹泉,胡 蕾,鄧承志

(1.南昌工程學院 江西省水信息協同感知與智能處理重點實驗室,江西 南昌330099； 2.江西師范大學計算機信息工程學院,江西 南昌330022)

1 引 言

高光譜遙感具有光譜分辨率高、圖譜合一和光譜波段數目多等特點,已成為地質制圖、植被調查、海洋遙感、環境監測等領域的重要技術[1]。然而,受成像光譜儀空間分辨率的限制和自然界地物復雜多樣的影響,混合像元普遍存在于高光譜遙感圖像中,其極大地限制了高光譜圖像的應用范圍[2]。混合像元分解是解決混合像元問題有效的方法,是保證高光譜遙感技術向定量化發展的前提[3]。

隨著端元光譜庫的普及以及稀疏表示理論[4]的迅速發展,Iordache等用已知端元光譜庫替代從圖像中選取端元集合,將稀疏約束引入到混合像元分解中,提出了稀疏解混的理論與方法[5]。稀疏解混不需要假設圖像中有純端元存在,同時不需要估計圖像中包含的端元數目,是當前解混的研究熱點[6]。稀疏解混的基本模型是一個非凸的組合優化問題,通常采用非平滑項“L0范數”表示。近年來,針對“L0范數最小化問題”提出了近似求解方法,最常見的是用L1范數代替L0范數[5]。對于L1稀疏正則化問題,變量分裂與增廣拉格朗日方法(Sparse unmixing by variable splitting and augmented lagrangian,SUnSAL)[7]被證實是有效的求解方法,可以得到較滿意的結果。然而,由于光譜庫中的端元數量與通常參與混合像元的組分數量之間的不平衡,導致L1正則化解混的稀疏性和穩健性并不好。為了更好地表征稀疏度,目前已涌現出一些方法,如吳澤彬等[8]采用迭代加權L1正則化方法、Sun等[9]采用L1/2稀疏正則化方法、Deng等[10]采用平滑L0稀疏正則化方法、Chen等[11]采用Lp稀疏正則化等。這些方法雖然改善了稀疏性,但當p<1時,Lp范數函數不是Lipschitz連續的,因此對于較小的p值存在數值求解問題。針對該問題,有學者提出利用指數函數、對數函數或sigmoid函數等Lipschitz連續函數逼近L0范數[12-13]。

TransformedL1(TL1)正則化函數[14]是一個由絕對值函數組成的雙線性變換的單參數族,與Lp(p∈(0,1])范數類似,通過控制參數a∈(0,∞)可任意表征L0和L1之間的范數,并滿足無偏、稀疏和Lipschitz連續的性質。鑒于TL1正則化函數具有的這些優勢,本文利用TL1正則化函數建立稀疏解混模型,并提出凸函數差分(Difference of Convex,DC)算法求解,即DCATL1算法。DCATL1算法收斂于滿足一階最優條件的駐點,對端元光譜庫矩陣是否滿足有限等距條件(Restricted Isometry Property,RIP)不敏感。

2 稀疏解混模型

線性混合模型假設在任何給定的光譜波段中,每個像元光譜是該像元中所有端元光譜的線性組合[2]。假設具有l個光譜波段,線性混合模型可描述成如下形式:

y=Mx+n

(1)

其中,y∈Rl×1表示某個像元的測量光譜；M∈Rl×q表示端元矩陣,q為端元數；x=[x1,x2,…,xq]T表示豐度向量；n∈Rl×1表示系統噪聲。

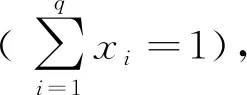
Iordache等[5]提出用已建立的地物光譜庫取代端元矩陣,以避免圖像中純凈像元不存在時無法提取完備的端元光譜。用已知的端元光譜庫A代替端元集合M,線性混合模型轉化為:

y=Ax+n

(2)

其中,A∈Rl×m是包含m條光譜曲線的端元光譜庫;x∈Rm×1為對應A中各端元的豐度向量。

光譜庫A中的端元光譜數m遠遠大于式(1)中的實際端元個數q,經稀疏分解獲取的豐度向量x也是稀疏的,即x中非零值的個數q?m,由此得到L0優化問題:

(3)

其中,第一項為重構誤差項,第二項為稀疏性約束項；λ是平衡保真項和正則項之間權重的參數；‖x‖0表示x的L0范數,用L0范數來統計x中非零元素的個數；x≥0和1Tx=1分別表示ANC和ASC。由于該問題是典型的非凸優化NP難問題,求解困難。2006年,Tao和Candès[14]合作證明了在滿足有限等距條件時,L0范數問題等價于L1范數凸優化問題:

(4)

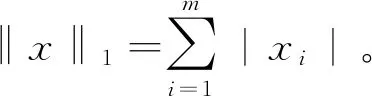
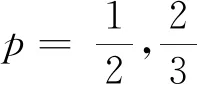
因此,本文提出了一種比L1范數更稀疏且易于求解、對端元光譜庫是否滿足有限等距條件不敏感的函數作為豐度稀疏約束項。

3 TL1正則化稀疏解混模型

TL1正則化函數ρa(x)[15]的定義:

(5)

ρa(x)是一個由絕對值函數組成的雙線性變換的單參數族,具有無偏性、稀疏性和連續性[16-17]。隨著參數a的變化,ρa(x)可以準確表征L0和L1之間的任意范數,近似Lp(p∈(0,1])范數。

從圖1中可看出,a的值越大,曲線越接近|x|,a的值越小,曲線越趨于坐標軸。從圖2中可看出,當a→∞,p=1時,ρa(x)和xp近似,逼近L1范數；當a→0,p→0時,ρa(x)和xp均趨于指示函數,逼近L0范數；在0≤x≤1范圍內,ρa(x),a∈(0,∞)和xp,p∈(0,1]可以相互近似。

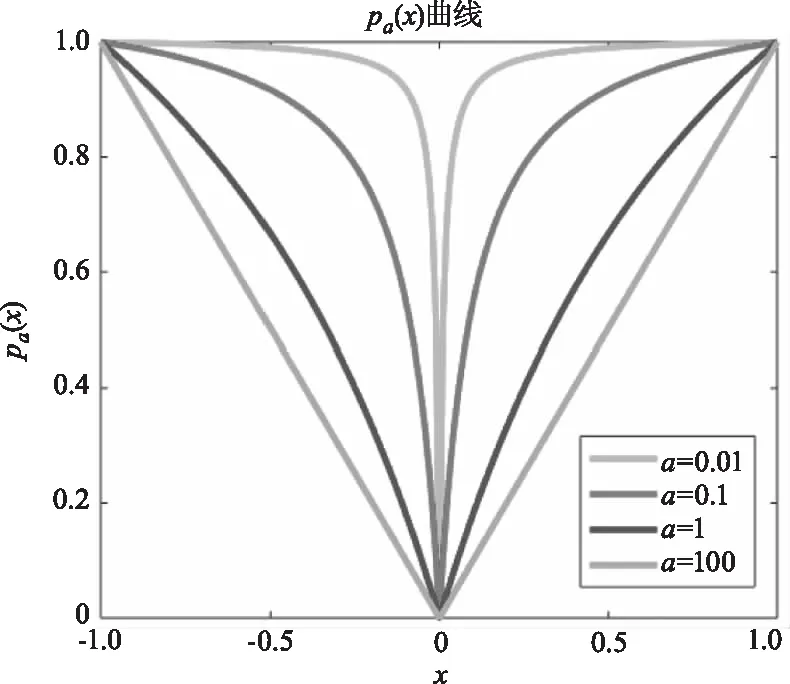
圖1 參數a=0.01,a=0.1,a=1,a=100時,ρa(x)的曲線

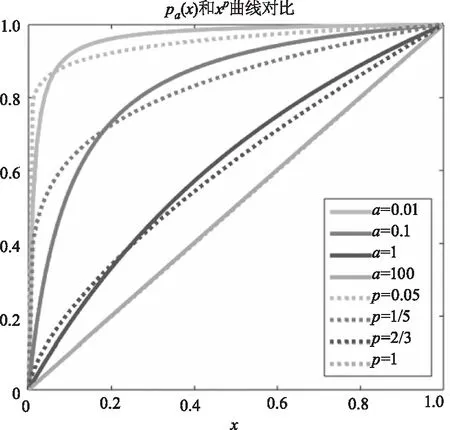
圖2 參數a和p取不同值時,ρa(x)與xp曲線對比

將TL1的定義擴展到向量空間,向量x=(x1,x2,…xN)T∈RN,定義:

(6)

通過調整參數a,用TL1代替L0范數來解決高光譜稀疏解混問題,得到TL1正則項最小化模型:

(7)

4 TL1正則化解混數值求解

本文采用凸函數差分(DC)算法求解TL1正則化稀疏解混變分問題,即DCATL1算法。DCATL1求解算法包括外層和內層循環迭代,外層循環采用DC算法,將非凸的TL1正則化函數表示為兩個凸函數之差,每步迭代求解一個強凸的L1正則化子問題,內層循環采用交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)[7]求解L1最小化問題。

將TL1正則化函數ρa(·)表示為兩個凸函數之差:

(8)

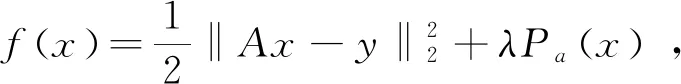
(9)

(10)

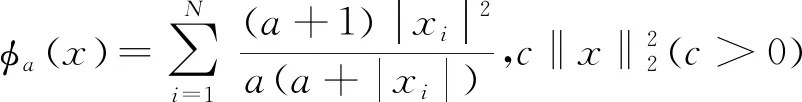
在迭代點xn,用函數h(x)近似表示其仿射函數hn(x)[19]:

hn(x)=h(xn)+〈x-xn,vn〉,vn∈?h(xn)

?h(xn)=λ?φa(xn)+2cxn

次微分?h(x)在x∈dom(h)是閉凸集,可做如下等價變換[19]:

inf{g(x)-hn(x):x∈RN}?inf{g(x)-〈x,vn〉:x∈RN}

定義上式的最優解為xn+1,則每步迭代解決以下強凸的L1正則化子問題:

(11)

使用ADMM方法求解式(11),引入變量z,并定義增廣拉格朗日函數:

(12)

其中,uT是拉格朗日乘子;δ>0是罰參數。

對目標函數L(x,z,u)求偏導,分別得到x,z,u的最優解表達式:

xk+1=B-1W

(13)

(14)

uk+1=uk+δ(xk+1-zk+1)

(15)

其中,B=ATA+2cI+δI,W=ATy+vn+δzk-uk。

shrink(·,·)是軟閾值算子,定義如下:

shrink(x,r)i=sgn(xi)max{|xi|-r,0}

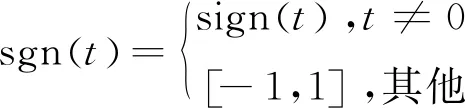
考慮ANC和ASC條件,最優化問題轉換為:

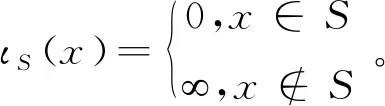
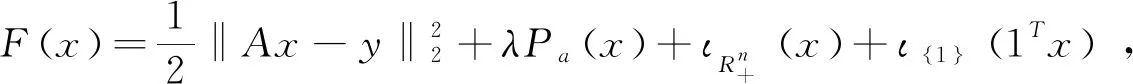
(16)

相應地,求最優解xn+1的子問題轉換為:

(17)

使用ADMM方法求解式(17),可得:

xk+1=B-1W-C(1TB-1W-1)

xk+1=max(xk+1,0)

其中,C=B-11(1TB-11)-1。

綜上所述,TL1正則化稀疏解混模型在ANC和ASC約束下的DC求解算法DCATL1如下:

5 實驗與分析

5.1 模擬數據實驗

模擬實驗端元光譜庫A由USGS光譜庫splib06(包括498條光譜,每條光譜224個波段)中任意選擇240條光譜曲線構成,即A∈R224×240,光譜范圍0.4～2.5 μm。每個模擬高光譜圖像由100個混合像元構成。豐度系數矩陣隨機生成,且滿足Dirichlet分布。生成3組高光譜模擬數據SD1、SD2、SD3,端元數k分別為2、4、6。在高斯白噪聲污染的情況下進行實驗,信噪比分別為30 dB、40 dB、50 dB。

采用信號重建誤差比(Signal-to-Reconstruction Error,SRE),進行定量分析,其定義如下:

(18)

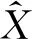
明算法的解混精度越高。同時,采用稀疏度(sparsity)[20]評價各解混算法豐度系數的稀疏性。稀疏度越小,表明得到的解越稀疏,解混效果越好。

表1給出不同信噪比和端元數情況下,SUnSAL和DCATL1算法獲得的SRE(dB)和sparsity值(均為100次平均值),以及相應的正則化參數取值。可以看出DCATL1算法在所有情況下都獲得了比SUnSAL算法高的SRE(dB)值,表明DCATL1算法的解混精度優于SUnSAL。在端元數量較少時(k=2),DCATL1的性能優勢更加明顯。同時,與SUnSAL算法相比,DCATL1算法獲得更稀疏的結果,表明TL1正則化模型能夠增強解的稀疏性。

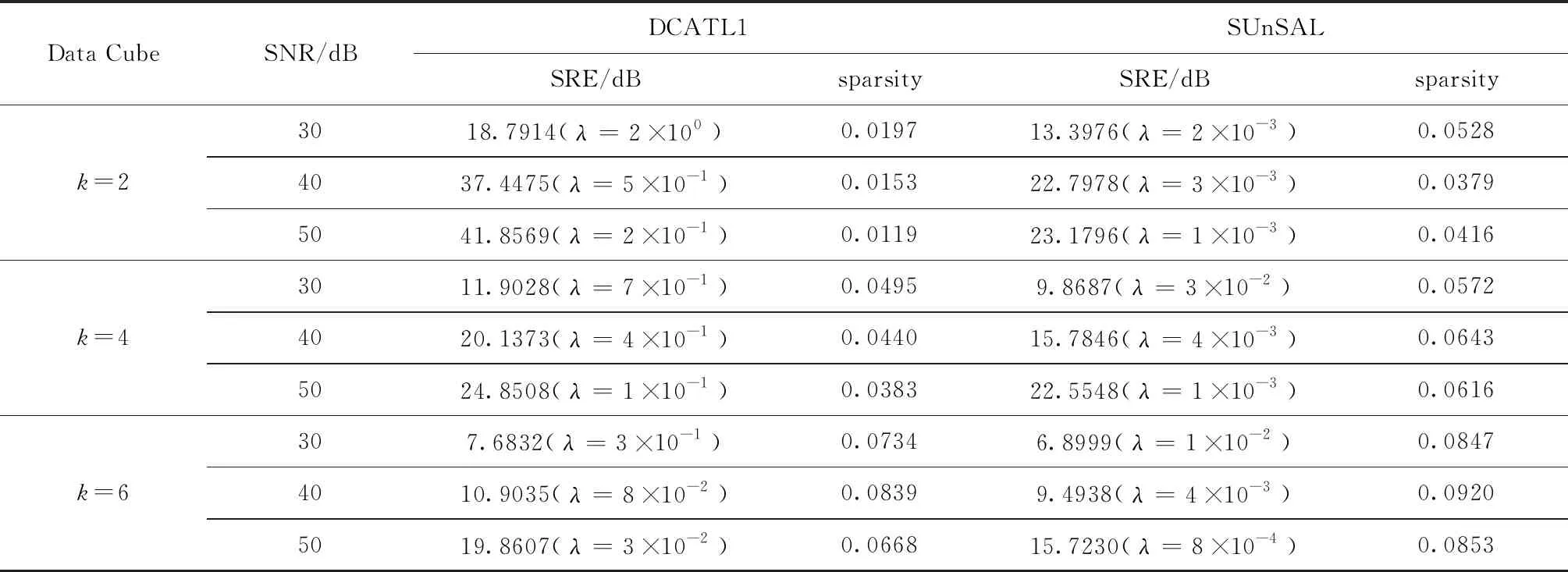
表1 各解混算法得到的SRE(dB)(a=100)和sparsity值

為進一步說明DCATL1的性能,圖3給出在信噪比為30 dB的模擬數據集SD1上,兩種解混算法的估計豐度圖及真實豐度圖。從圖中可以看出,DCATL1估計出的豐度圖比SUnSAL更接近于真實的豐度。SUnSAL估計出的豐度圖中存在較多干擾豐度或者噪聲,而DCATL1消除了大部分干擾,體現了TL1正則化模型比L1模型具有更好的稀疏性和更高的解混精度。

在稀疏解混算法中正則化參數λ可以平衡解的精確性和稀疏性。為分析參數λ對DCATL1算法的影響,圖4繪制了信噪比分別為30 dB、40 dB和50 dB的情況下,端元數分別為2、4和6時,SRE(dB)值隨參數λ的變化曲線。從圖4中可以看出,隨著信噪比的增大,λ最優取值越小,隨著端元數減少,λ最優取值越大。在這幾種不同的情況下,λ最優取值趨勢基本類似,且參數的可選范圍較大。

5.2 真實數據實驗

為了驗證DCATL1算法在真實高光譜圖像場景下的有效性,采用美國內達華州的AVIRIS Cuprite(赤銅礦)遙感圖像數據進行實驗。選取250×191的像元子集,包括224個光譜波段,波長范圍0.4～2.5 μm。去除1～2、105～115、150～170和223～224等低信噪比和水蒸氣的吸收波段,剩下188個光譜波段數。圖5顯示了1995年通過USGS拍攝得到的礦物圖,利用Tricorder 3.3軟件[21]產品反映Cuprite礦區數據中各礦物的分布情況。在實驗中,圖5顯示的礦物圖作為各算法定性分析的參考,用它來判斷各算法是否將該數據中的礦物分解出來了。

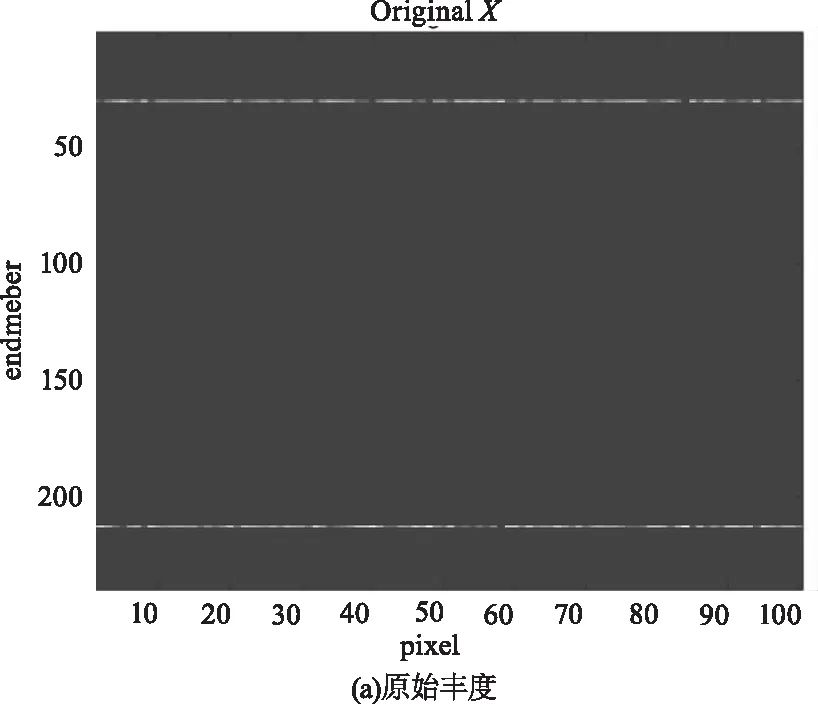
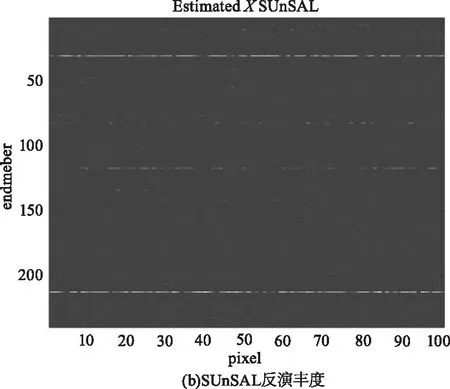
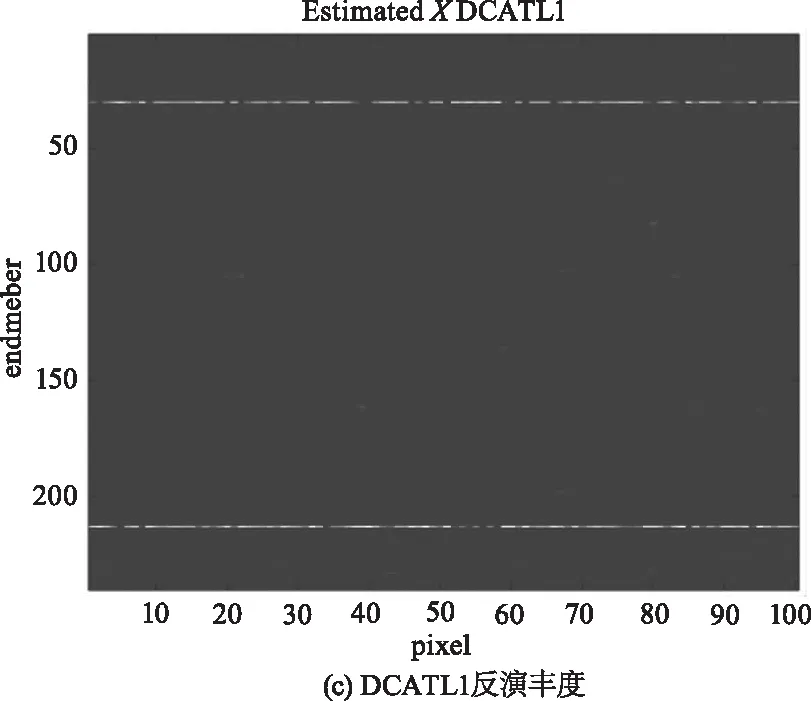
圖3 SNR=30 dB時,模擬數據 SD1的反演豐度與原始豐度對比

實驗利用SUnSAL和DCATL1算法分別對該Cuprite高光譜數據進行混合像元分解,估計出各端元的豐度圖像并進行展示。選擇Alunite(明礬石)、Buddingtonite(水銨長石)和Chalcedony(玉髓)三種礦物的Tricorder 分類圖作為定性分析的參考,分析兩種算法的性能。實驗中,SUnSAL和DCATL1算法的正則化參數經驗性地分別設置為λ=0.001,λ=0.2。

如圖6所示,兩種算法分解出來的效果與Tricorder分類圖都較相似,表明了稀疏解混算法的有效性。

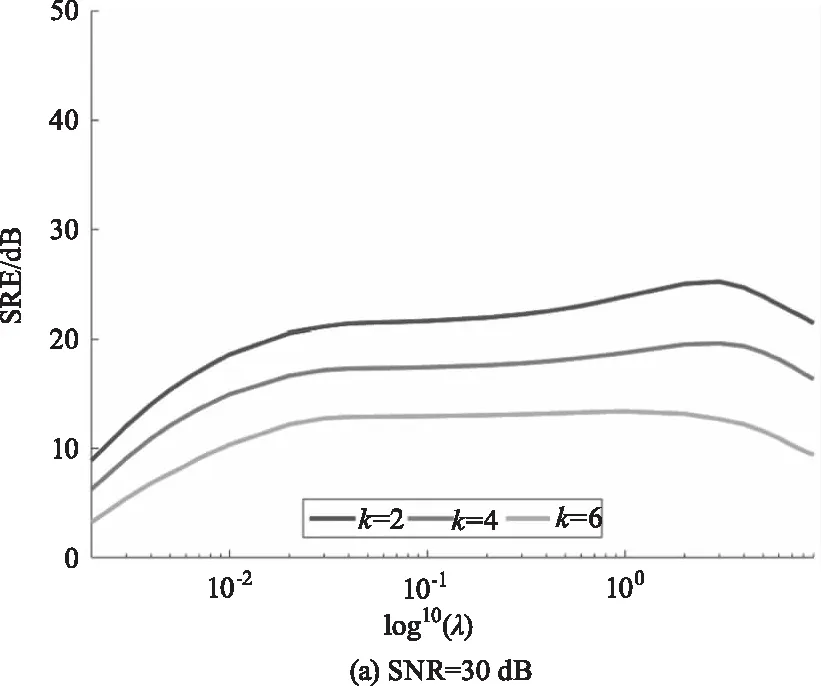
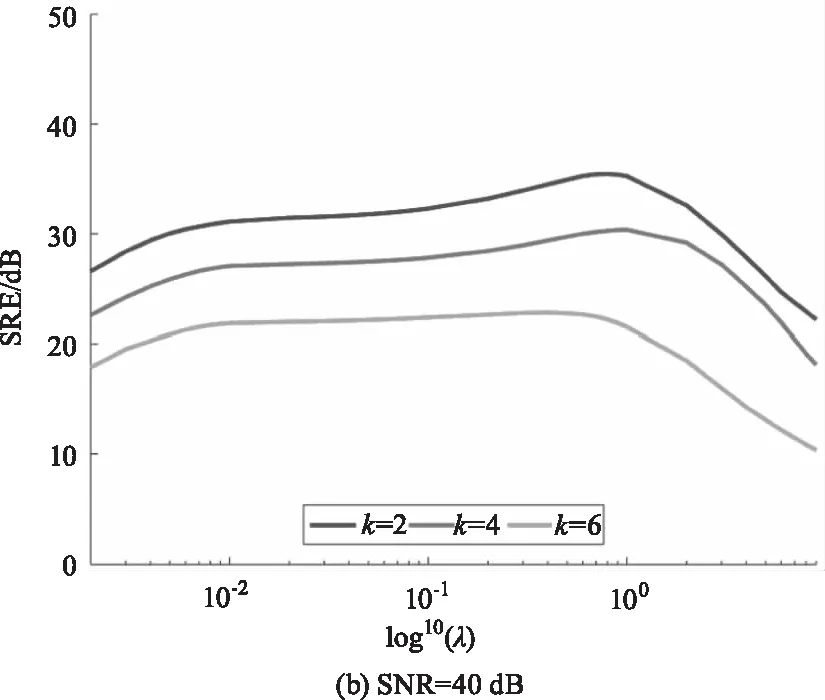
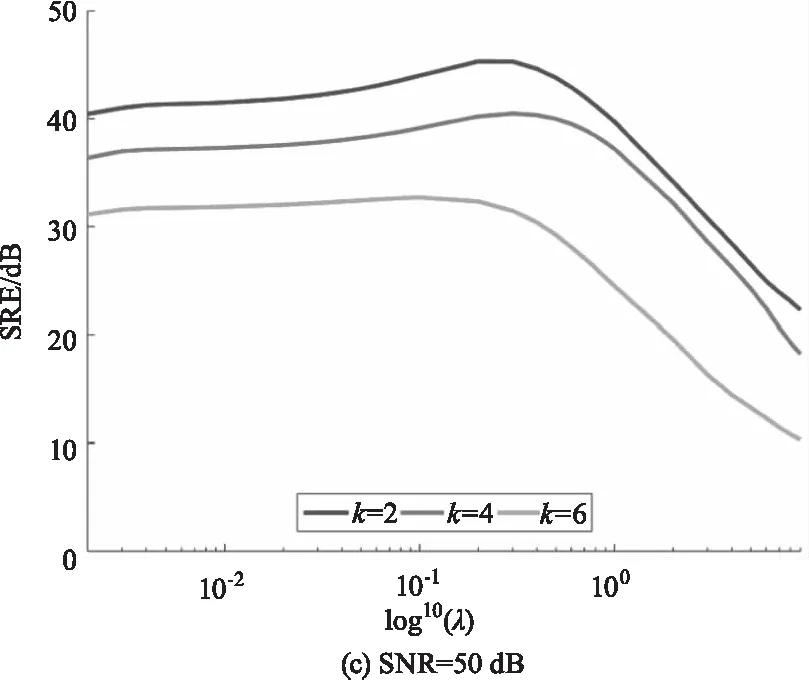
圖4 不同信噪比和端元數情況下,DCATL1算法

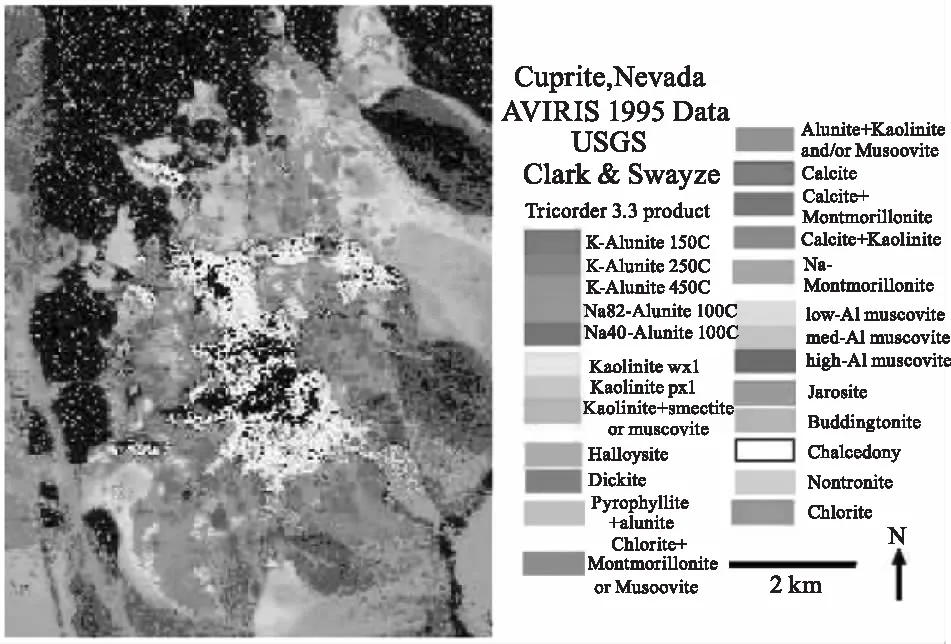
圖5 USGS獲得的內華達州赤銅礦區不同礦物所在的位置

然而,從圖6中可以看出,DCATL1算法估計的豐度圖(如Alunite明礬石)噪聲較少,更接近于真實的參照圖。此外,也計算了SUnSAL和DCATL1算法獲得的稀疏度(sparsity),分別為0.0718和0.0459。從這些小的差異可以得出結論,本文提出的DCATL1算法使用了更少數量的像元來表達數據,具有更高的稀疏性。通過真實數據實驗得到的結果表明,DCATL1算法能夠提高解混精度。

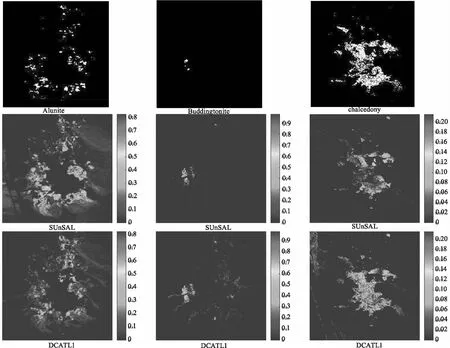
圖6 在真實數據實驗下SUnSAL和 DCATL1算法分別得到的礦物豐度圖

6 結 論

本文提出TL1正則化的高光譜圖像稀疏解混模型及其求解算法DCATL1,用稀疏、Lipschitz連續的TL1正則項代替稀疏回歸模型中的L0范數,利用DC算法將非凸的TL1正則項函數分解為兩個凸函數之差,再運用ADMM算法解決凸的子問題。TL1正則化模型比L1正則化模型具有更好的稀疏性和更高的解混精度。通過模擬和真實的高光譜數據集進行實驗,驗證了該方法的有效性和準確性。參數a依賴先驗知識進行初始化。下一步將研究參數a的自適應選取,使目標函數由近似L1范數開始,當算法收斂到初始最優解時,通過迭代更新得到L0范數最小化的精確近似值,以提高算法自適應能力。