基于多智能體深度確定策略梯度算法的有功-無功協調調度模型

趙冬梅 陶 然 馬泰屹 夏 軒 王浩翔

（1. 華北電力大學電氣與電子工程學院 北京 102206 2. 國網紹興供電公司 紹興 312000）

0 引言

我國資源和負荷分布不均勻，能源利用不充分，遠距離輸電的格局已基本形成。文獻[1-3]做出了關于“未來一體化大電網調控系統”的前瞻性研究，設計了大電網全局決策和監控框架。有功-無功協調調度是實現大電網智能調控、自動巡航的關鍵一環，是保證電網經濟和安全運行的前提之一。

文獻[4-6]基于網絡特性，利用二階錐松弛理論，實現配電網有功-無功的協調優化計算。然而，二階錐松弛技術的計算速度無法達到較大電網的調度需求[7]。文獻[8]分析了無功電壓優化對新能源消納的影響。文獻[9]基于模型預測控制研究了配電網動態無功優化方法。文獻[10]基于多目標優化算法研究了中壓配電網中有功-無功的協調優化。文獻[11]研究了考慮配網重構的多時間尺度無功優化。文獻[12]研究了光伏并網系統的有功-無功控制問題。有功控制對象和無功控制對象通常分屬于不同的地區和調度主體，部分控制目標之間存在沖突。在決策角度上，上述研究不能較好地解決有功-無功調度間的矛盾。

進而，實現有功-無功協調調度需要智能組織電力系統中的靈活調控資源，系統的靈活調控資源包含可調度常規能源、需求側管理、儲能和與其他互聯市場的交易等[13]。但是，靈活多調控資源在最大化自身收益和優化區域調控指標間具有難以調和的矛盾，智能組織多種靈活調控資源是當前一大熱點和難點。

多智能體技術是一類基于協同一致性原理，用于探索環境、解釋未知、自主更新和協調沖突的有效技術。實現多智能體系統的“智能”可以運用強化學習方法。強化學習通常分為兩類：①值迭代（value based）；②策略迭代（policy gradient）。文獻[14-21]將值迭代類型的強化學習方法運用到電力系統中的優化調度、控制等領域。而受到Q 表存儲和搜索的限制，智能體的狀態空間和動作空間必須是離散的、低維的。上述研究均是采用將連續動作空間離散化的類似處理方法。在運用到有功-無功協調中時可能會損失一部分精度，且對訓練過程中新出現的未知狀態和動作適應性不強。

相比值迭代類的強化學習方法，采用策略迭代更加適用于解決電力系統有功-無功協調這類擁有連續、高維狀態和動作空間的問題。由于該種算法直接由策略梯度更新神經網絡參數，各智能體的動作選擇差異會導致環境發生變化，影響了智能體在動作選擇時的收斂性。所以，此類方法在電力系統中的應用較少。針對上述問題，本文在對各類算法和多智能體環境探索的基礎上，提出適用于本文控制模型的改進多智能體深度確定策略梯度算法（Multi-Agent Deep Deterministic Policy Gradient,MADDPG）。在智能體更新時考慮其他智能體的動作選擇，從而提高在多智能體環境中各智能體的訓練效果。同時，搭建分層多智能體有功-無功協調調度框架；設計電力系統多智能體環境；構造狀態空間、動作空間和智能體獎勵函數表達。最后，通過算例仿真和對比分析，驗證本文所提模型及算法的優勢和有效性。

1 分層多智能體有功-無功協調框架

多智能體系統是分布式控制中的一種技術體現，分布式系統通常有四種組織形式[22]。分布式（distributed）的系統組織形式在通信成本、運行成本和可行性等方面具有一定優勢。

基于此，將受控電網劃分為不同的區域。統籌區域內靈活有功-無功調控資源，參考國際能源署（International Energy Agency, IEA）對靈活調控資源的定義，將區域中的有功-無功調控資源分為：常規機組智能體（Conventional Unit Agent, CUAgent）、電儲能智能體（Electric Energy Storage Agent,EESAgent）、風/光電智能體（Wind-Solar Power Agent，WSAgent）、可投切電容器智能體（Switchable Shunt Capacitor Agent, SSCAgent）、有載調壓變壓器智能體（On-Load Tap Change Agent, OLTCAgent）和連續無功補償智能體（Continuous Reactive Power Compensation Agent, CRPCAgent）。智能體組織關系如圖1 所示。

圖1 智能體組織關系示意圖Fig.1 Schematic diagram of organization of agents

全局主智能體（Global Master Agent, GMAgent）直接協調各區域智能體（Regional Agent, RAgent），RAgent 控制了區域中的各個智能體：常規機組智能體CUAgent、電儲能智能體EESAgent、風/光電智能體WSAgent、無功補償智能體（Q Compensation Agent, QCAgent)。其中，QCAgent 下設可投切電容智能體SSCAgent、連續無功補償智能體CPRCAgent、有載調壓變壓器智能體OLTCAgent。全局主智能體GMAgent 監控全網狀態，根據調度中的功率平衡需求確定調度方向，并將調度方向信息下發，調度方向的確定有利于提高各智能體的訓練速度和輸出正確的調度指令。區域智能體RAgent 接受GMAgent的信息，之后將采集到的本區域電力系統的狀態信息經篩選和歸一化處理后發送給下級各智能體。模型建立以省-地兩層調度為基礎。

1）常規機組智能體CUAgent 建模

CUAgentj的運行成本主要考慮發電成本和輔助服務補償。輔助服務補償包括響應自動發電控制（Automatic Generation Control, AGC）補償、啟停調峰補償、深度調峰補償和冷/熱備用補償，如式（1）所示。

視常規機組發電成本為二次函數，則

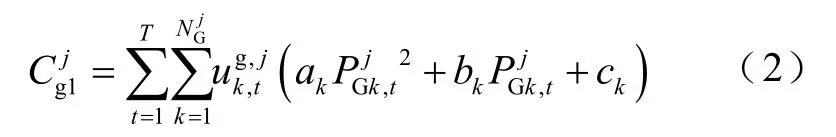
式中，T為調控周期；上標j為CUAgent 的控制區域；為常規機組數量；為機組啟停0-1 狀態變量；為常規機組出力；ak、bk和ck為發電機二次成本函數系數。

當電網中功率波動需要AGC 作用時，安裝AGC裝置的發電機需要動作，可能失去在電能量市場獲利的機會，并對機組產生損耗，除了機組在爬坡過程付諸的成本外，還需要按調節容量和調節電量獲得補償，如式（3）～式（5）所示。

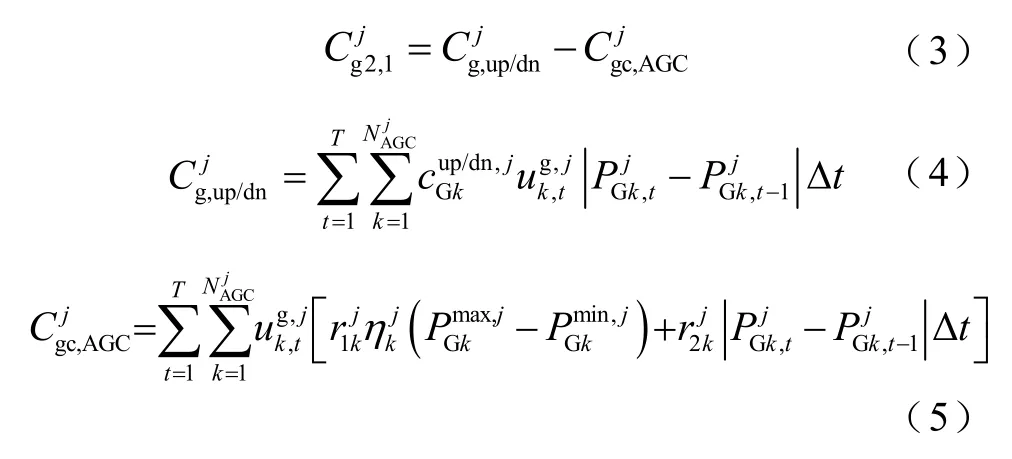
當電網中因為調峰要求需要啟停機組，除了計算啟停成本外，如果在停機后24h 內又因為調峰原因開啟同一臺機組，則按停機容量進行補償[23]，如式（6）所示。

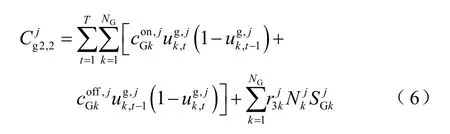
當機組運行在基本調峰需求基準以下時，稱為深度調峰，按少發電量進行補償[24]。

因電網調峰需求停機，在24h 內啟機則按啟停調峰進行補償，若在24h 內繼續保持停機，則按機組冷備用進行補償；若機組出力高于深度調峰基準，而又未達到機組計劃出力，則按機組熱備用進行補償，如式（8）所示。

綜上所述，常規機組智能體CUAgentj的綜合收益為

2）電儲能智能體EESAgent 建模

EESAgentj的運行成本主要考慮購電成本和運維成本，如式（10）所示。

式中，上標j為在EESAgentj的控制范圍內；為電儲能數量；為電儲能k的離網/并網0-1狀態變量；為第k個電儲能向電網購電的價格，元/(MW·h)；為電儲能k的單位運維成本，元/(MW·h)；分別為電儲能k的充、放電功率。

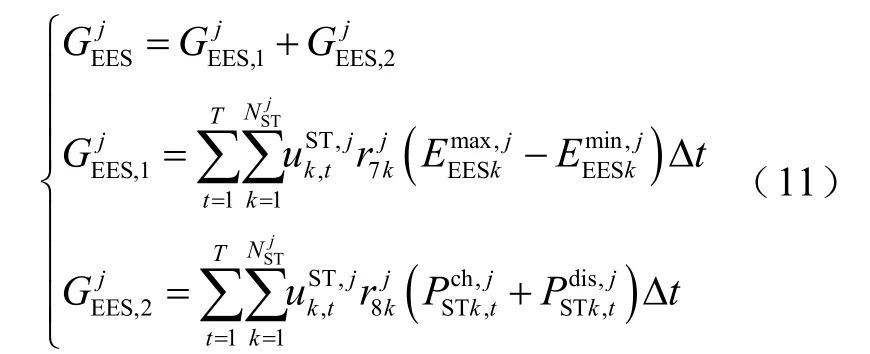
綜上所述，電儲能智能體EESAgentj的綜合收益為

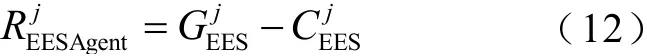
3）風/光電智能體WSAgent 建模

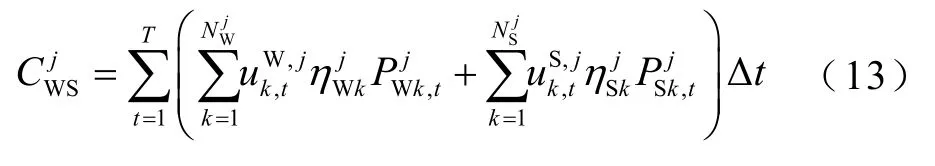
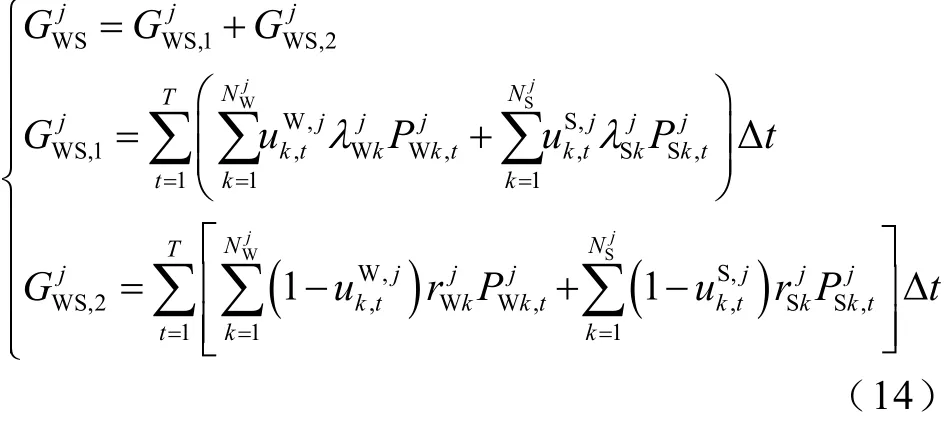
綜上所述，風/光電智能體WSAgent 的綜合收益為

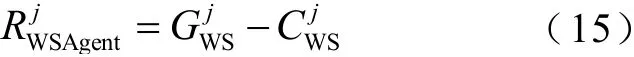
4）無功補償智能體QCAgent 建模

區域無功調度任務由常規機組智能體CUAgent、可投切電容智能體SSCAgent、有載調壓變壓器智能體OLTCAgent 和連續無功補償智能體CRPCAgent共同完成。SSCAgent、OLTCAgent 和CRPCAgent的無功補償功能本質上是相同的，只在約束條件上稍有差別，且在運行過程中沒有額外成本的產生。因此，只對這三種智能體設有“動作執行”的功能，而向上設置具有通信、決策、動作等完全功能的無功補償智能體QCAgent。

SSCAgent、OLTCAgent 和 CRPCAgent 接收QCAgent 的無功控制指令是沒有差別的，只受到網絡拓撲的影響，根據獎勵函數不同做出不同的動作，需要設計綜合網損和節點電壓偏差量的收益函數，并將OLTCAgent 的擋位調整的動作轉換成注入無功功率的調整。控制區內電壓與無功的關系由式（16）含靈敏度矩陣的線性方程組給出。

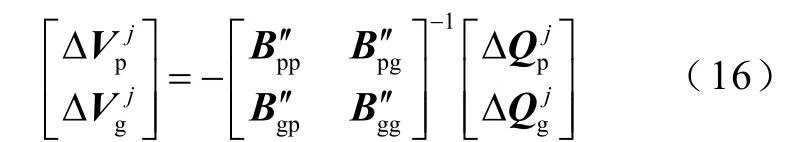
OLTCAgent 檔位調整與無功/電壓的關系為

式中，bii和bij分別為節點i的自導納和支路ij的互導納。

QCAgentj的運行成本CQCAgent為

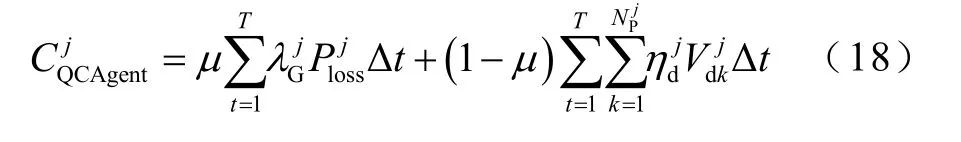
在CUAgent 與QCAgent 通信過程中，得到信息需要響應QCAgent 的無功控制指令時，由于受到發電機功率極限的限制，常規機組不得不放棄在電能量市場獲利的機會，而為區域提供無功支撐。CUAgent 少獲得的利潤記為QCAgent 的調節成本，如式（20）所示。

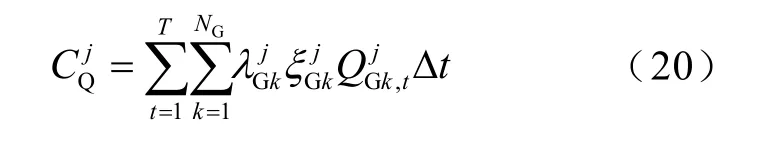
式中，為常規機組k的有功-無功轉換系數，表征受發電機功率極限圖限制下的無功出力對應的有功功率。

式（9）、式（12）、式（15）和式（20）是對各智能體收益的數學表達，即為各智能體在訓練中的目標函數。

2 深度強化學習算法設計

2.1 MADDPG 算法

多智能體深度確定策略梯度算法（MADDPG）是一種適用于多智能體系統的深度強化學習算法[27]，它最先由OpenAI 的研究人員提出[28]。

MADDPG 算法構建演員網絡（Actor Network）和評論家網絡（Critic Network）兩個神經網絡。演員網絡將策略梯度和狀態-行為值函數相結合，通過優化神經網絡參數θ來確定某狀態下的最佳行為。評論家網絡通過計算時間差分誤差（temporal difference error）來評估演員網絡產生的行為。每一個演員網絡和評論家網絡中又同時構建兩個結構完全相同，但參數不同的神經網絡，分別稱為估值網絡（evaluation network）和目標網絡（target network）。估值網絡的參數是隨著訓練而不斷更新的，目標網絡不進行訓練，它的參數是一段時間前的估值網絡的參數。MADDPG 算法中神經網絡結構如圖2所示。

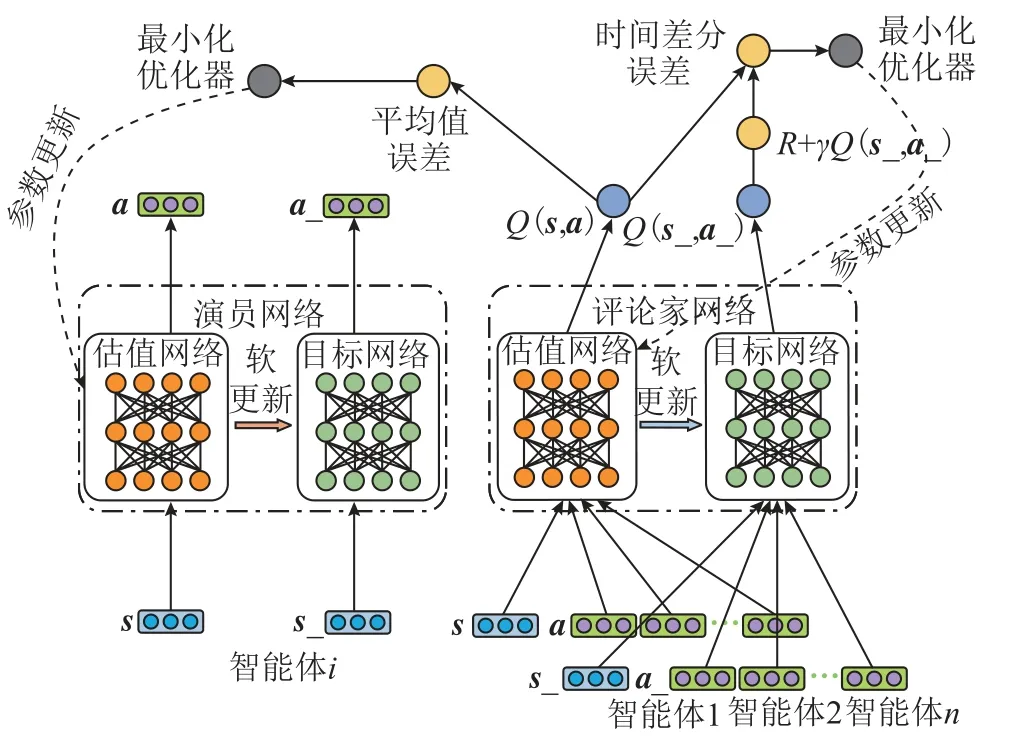
圖2 MADDPG 算法神經網絡結構Fig.2 Neural network structure of MADDPG algorithm

圖2 中，s和s_分別表示輸入估值網絡和目標網絡的所有智能體的狀態。MADDPG 算法實際上是一種部分觀測的馬爾科夫決策，它對狀態集的要求并不嚴格，對分區智能體可以只對神經網絡輸入本區域內智能體的狀態s，即觀測o。a和a_分別表示輸入估值網絡和目標網絡的所有智能體的動作。

設有n個智能體，n個智能體是集中訓練、分散執行。n個智能體的權重參數集為觀測集為；動作集為策略集為

智能體i獎勵的期望值的策略梯度（下文簡稱為策略梯度）為

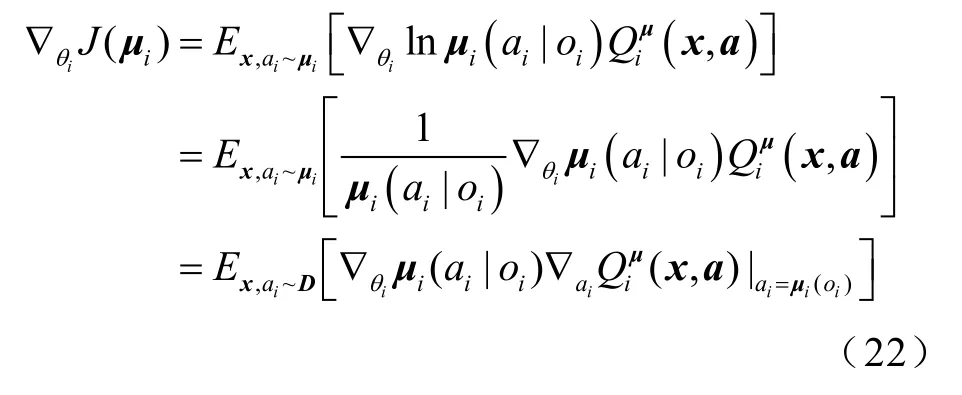
演員網絡通過最大化狀態-動作值函數Q(s,a)來更新網絡參數，目標函數及參數更新規則分別為

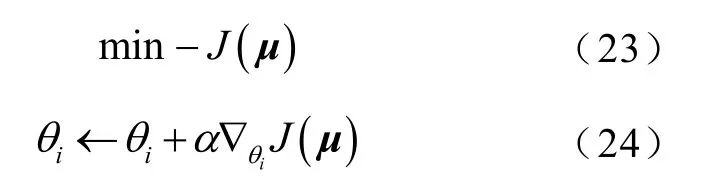
式中，α為更新步長，即學習率。

評論家網絡的損失函數為

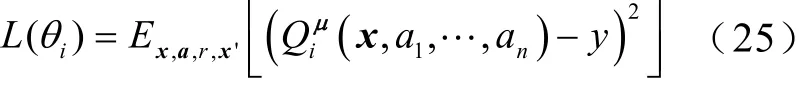
其中

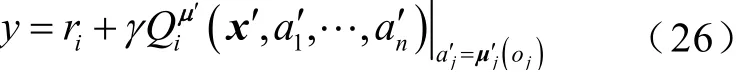
評論家網絡通過最小化時間差分誤差來更新網絡參數，目標函數及參數更新規則分別為

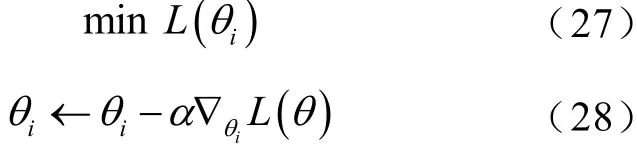
為了提高神經網絡訓練時的收斂速度和防止過擬合，每一次訓練時，都從經驗回放緩存區中隨機采樣一組記憶，輸入到神經網絡進行訓練。

最后，即可通過式（29）所示的軟更新策略，更新目標網絡的參數。

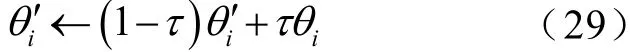
式中，τ為軟替換（soft replacement）系數，且分別為智能體i的目標網絡參數和估值網絡參數。

2.2 狀態-動作空間

對于電力系統的有功無功協調控制模型，狀態空間的選取既要可以表征智能體執行某一動作iA后電力系統全面而真實的物理狀態，又不能對神經網絡的訓練帶來太多的計算負擔。因此，本文將系統中每一個節點的電壓相角、電壓幅值、節點注入有功功率和無功功率作為電力系統的狀態量輸入進神經網絡，如式（30）所示。

式中，Va、mV、Pbus和Qbus分別為節點的電壓相位、電壓幅值、注入有功功率和注入無功功率的向量。

本文智能體的動作設計比較直觀，均為各智能體的動作值。如CUAgent 的動作空間是其出力上下限的連續實數集。

2.3 獎勵函數

獎勵函數的正確設計是強化學習算法高效運作的必要條件。本文模型中獎勵函數的設計有兩個要點：①可以被準確量化并分布到智能體的每一動作；②獎勵值必須來源于環境或與環境具有較強的關聯。而僅按智能體實際收益設計CUAgent、WSAgent、EESAgent 的獎勵函數與電力系統環境的耦合度依然不足，系統中平衡節點機組的有功出力容易越界，既不符合電力系統運行要求，又增加了智能體在不可行空間的探索次數。

由于CUAgent、WSAgent 和EESAgent 在環境中探索過于貪婪或保守，可能導致平衡節點機組出力越界。因此，需要附加智能體j的過貪婪/過保守懲罰量PUNAgentj。智能體j的綜合獎勵函數為

式中，rP為越界懲罰系數；為平衡節點機組的上網電價；分別為平衡節點機組的出力下、上界；為平衡節點機組出力；αj和βj分別為智能體j的過貪婪和過保守懲罰系數，計算式為

3 算例仿真

本文在某節點系統的基礎上進行改進，從某電網SCADA 系統采集連續100 天真實節點有功、無功負荷數據（采樣周期為15min），用以訓練智能體的神經網絡。設置5 個CUAgent（所在節點：1,2,3,6,8）；1 個WSAgent，含一個風電機組群（所在節點：5）和光伏機組群（所在節點：7）；1 個EESAgent（所在節點：4）；2 個SSCAgent（所在節點：9,10）；3 個OLTCAgent；2 個CRPCAgent（所在節點：11,12）。模型中的各參數按照其單位同比縮放。使用Python 編程，利用tensorflow 框架，搭建多智能體神經網絡計算圖（Graph）。

仿真測試硬件平臺：Intel(R) Core(TM) i7-9700 CPU @ 3.00GHz；8GB 2666MHz RAM；GPU：NVIDIA GeForce GTX 1660 Ti；軟件平臺：Deepin 15.11（Linux 4.15）；Python 3.7.3；Tensorflow 1.14.0。

神經網絡結構及超參數見表1。

表1 神經網絡結構及超參數Tab.1 Neural network structure and hyperparameters

在神經網絡訓練過程中，使用Google 開發的深度學習可視化工具Tensorboard，采樣并導出各個智能體評論家網絡的狀態-動作值函數Q(s,a)、估值網絡與目標網絡參數的時間差分誤差?Q(s,a;θ)來評估各智能體演員網絡和評論家網絡的訓練效果，計算式為

為了便于歸一化分析，狀態-動作值函數Q(s,a)也取其時間差分ΔQ(s,a;t)，計算式為

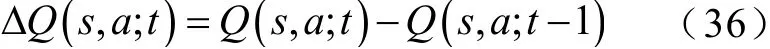
訓練結束時，各智能體狀態-動作值函數時間差分值、神經網絡參數的時間差分誤差分別收斂于數量級，智能體的動作選擇趨于穩定，估值網絡和目標網絡參數更新也不再明顯，驗證了MADDPG 算法在本文所提模型與調度問題中運用的有效性。

4 對比分析

4.1 與傳統有功-無功解耦調度模型對比

選取除訓練集外的某電網SCADA 系統采集的1 天96 個時段的真實節點有功、無功負荷數據，用以對比分析本文所提有功-無功協調模型（下稱：協調調度）與傳統有功-無功解耦調度模型（下稱：解耦調度）的調度效果。解耦調度以經濟調度[29]與無功優化為基礎，并用二階錐松弛技術[4]處理非凸、非線性的潮流方程約束，目標函數是最大化智能體收益的總和。

比較分析CUAgent、WSAgent 在兩種調度模型下的動作情況，以及系統非壓控節點電壓幅值變化、網損變化。協調調度和解耦調度對比分析效果如圖3a～圖3h 所示。系統總有功、無功負荷如圖3i 所示。

如圖3a、圖3b 所示，采用協調調度的CUAgent相比采用解耦調度的CUAgent 在動作選擇傾向上，有明顯的不同。采用解耦調度的各CUAgent 基本跟隨負荷的變化呈現同升同降的趨勢，而采用協調調度的各CUAgent 在均衡各自收益下，不斷維持最大化自身收益，并保證功率的實時平衡。CUAgent 2、4、5 的出力在96 時段中，出力基本持平，而將系統跟隨負荷變化的調度任務交給性能更好的CUAgent 1、3。如圖3c、圖3d 所示，協調調度：96 時段總棄風207.53MW（3.65%）、總棄光171.89MW（9.6%）、總棄風/光新能源379.42MW（5.08%）；解耦調度：96 時段總棄風399.16MW（7.02%）、總棄光0MW（0%）、總棄風/光新能源399.16MW（5.34%）。盡管解耦調度中沒有出現棄光的情況，但從風/光新能源消納的總量上來看，協調調度較解耦調度提高風/光利用19.74MW（0.26%），說明協調調度是一種“協調統一、均衡收益”的策略，對電網調度機構、風電和光電等都較為公平與合理。如圖3e、圖3f 所示，采用協調調度控制，各非壓控母線電壓波動幅度更小，且沒有節點電壓越界，而采用解耦調度控制的節點電壓波動更大，且節點7、9、10、11 的電壓幅值，在部分時段越上界。如圖3g 所示，協調調度中，系統96 時段總網損為417.99MW（1.28%），解耦調度中，系統 96 時段總網損為 441.18MW（1.35%），協調調度較解耦調度降低系統有功網損23.19MW（0.07%）。如圖3h 所示，協調調度中，1～30 時段，風電大發，EESAgent 選擇在此時段調用自身容量儲備用以消納風電；在50～62 時段，光伏大發時，EESAgent 無可用容量，只得選擇棄風。解耦調度中，EESAgent 通過經濟調度優化算法，選擇在24～50 時段風電和光伏總和較大時，調用自身容量，減少風、光的棄用。

圖3 協調調度與解耦調度效果對比圖Fig.3 Comparison of coordination and decoupling dispatching

以上對比分析說明，協調調度相比解耦調度，在均衡各智能體收益，協調電力系統不同控制主體間的利益矛盾，消納風/光新能源，控制節點電壓波動、優化系統網損方面具有一定的優勢。

4.2 MADDPG 與其他強化學習算法對比

基于相同的電力系統環境配置，在策略迭代算法中選取DDPG 算法[30]，在值迭代算法中選取深度Q 網絡（Deep Q-Network, DQN）和深度雙Q 網絡（Double DQN, DDQN）[31]算法，與本文MADDPG 算法在神經網絡訓練效率、智能體動作選擇、電力系統網損和節點電壓偏差方面進行比較。值迭代算法DQN 和DDQN 狀態值的輸入與MADDPG 算法保持一致，但其動作值的輸入必須是離散的、有限的。為盡量保證與MADDPG 的可比性，將各智能體的連續動作區間均勻離散成 10 000 份，記為DQN-10 000 和DDQN-10 000。

將SCADA 系統每一個采樣周期時采集到的電力系統節點有功、無功負荷作為一個訓練集，共9 600 個訓練集。在智能體神經網絡訓練的每一個回合中，隨機采樣一個場景進行訓練，為了便于可視化說明，以下對比結果分析僅展示其中一個場景的訓練效果。

系統中非壓控母線的節點電壓幅值在訓練過程中的變化情況如圖4 所示。

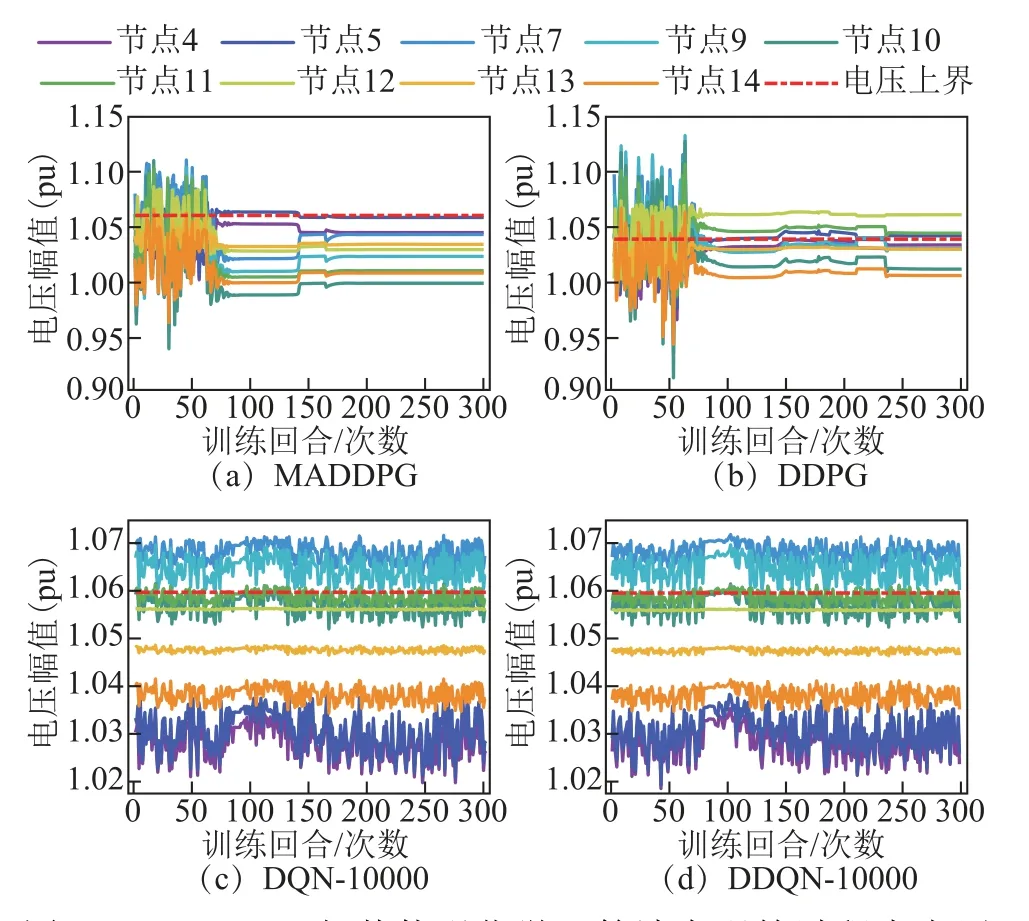
圖4 MADDPG 與其他強化學習算法在訓練過程中電壓幅值的變化Fig.4 Voltage amplitude changes during training of MADDPG and other reinforcement learning algorithm

MADDPG 和DDPG 分別在約160 和約260 訓練回合后，結束神經網絡訓練。而DQN-10 000 和DDQN-10 000 無法在可接受的時間內收斂。MADDPG 算法的訓練性能優于其他強化學習算法。MADDPG 算法中，所有節點電壓均在設定的范圍內，且逼近基準值1.0(pu)。而在DDPG 算法中，節點5、12 和13的電壓幅值越上界，且其余節點電壓逼近上界。在DQN-10 000 和DDQN-10 000 算法中，節點7、9 和11 電壓越限明顯。說明MADDPG 在控制節點電壓幅值相比其他強化學習算法具有一定優勢。

圖5 所示為算法訓練過程中CUAgent 動作選擇變化。各智能體的輸出層均采用雙曲正切激活函數，可以保證除CUAgent1 外各智能體的動作輸出不越界。為便于可視化分析，在DQN-10 000 和DDQN-10 000 算法中僅列出CUAgent1 的訓練結果。

圖5 中的兩條點劃線分別表示平衡節點機組智能體的出力上下界，分別為2.233(pu)和0.558(pu)。MADDPG 算法在第160 回合收斂，且平衡機組的出力保持在上、下界之間，而DDPG 算法中，在訓練過程中，平衡節點最終收斂到越過下界的值0.556(pu)。DQN-10 000 和DDQN-10 000 算法中的CUAgent1均未在可接受的時間內選擇到合適的動作值。

MADDPG 和其他強化學習算法訓練過程中全網網損的變化如圖6 所示。

DDPG 在神經網絡訓練時，沒有考慮其他智能體的動作。雖然網損優化結果（3.53MW）優于MADDPG 算法（7.13MW），但網損的優化是由于平衡節點機組出力越下界和抬高節點電壓以至于電壓越界而實現的，總有一部分智能體在環境中占據優勢，獲得更多的收益，而另一部分智能體則處于劣勢，導致某些電力系統的狀態量超出規定限度。DQN-10 000 和DDQN-10 000 在訓練中，全網的網損在10MW 附近變化，最終未能收斂。

在值迭代算法DQN-10 000 和DDQN-10 000 中，盡管將動作均勻離散成 10 000 份，但若想達到MADDPG 算法的動作選擇精度，則需要將動作進一步細化。而從上述給出的DQN-10 000 和DDQN-10 000 仿真結果來看，進一步切分動作會使算法收斂性進一步劣化。盡管理論上DDQN 算法的適應性強于DQN 算法，但DDQN-10 000 和DQN-10 000整體上區別不大，可見基于值迭代的方法無法較好地適用于本文模型。

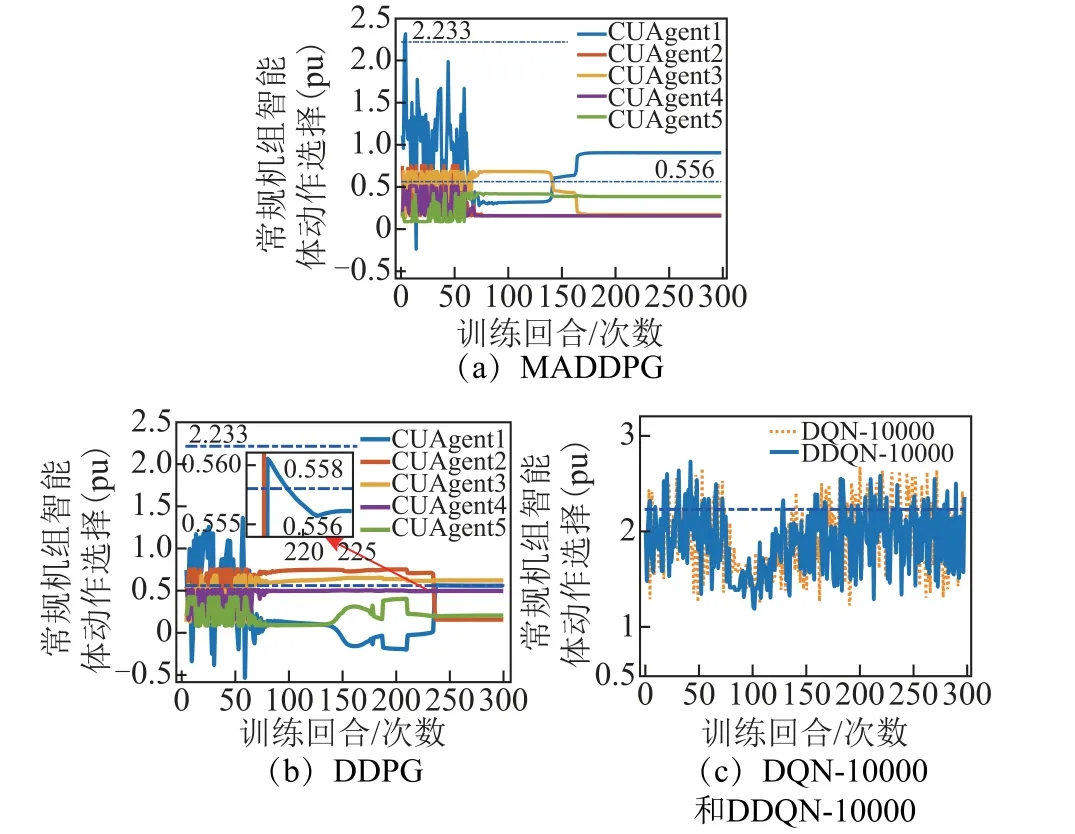
圖5 MADDPG 與其他強化學習算法在訓練過程中CUAgent 動作選擇變化Fig.5 Action choices of CUAgent during training of MADDPG and other reinforcement learning algorithm

圖6 MADDPG 和其他強化學習算法在訓練過程中網損的變化Fig.6 Transmission losses changes during training of MADDPG and other reinforcement learning algorithm

綜上所述，MADDPG 算法無論是在實現各智能體間收益的均衡、協調各智能體間矛盾、還是輸出符合約束的電力調度指令上，都具有一定的優勢。

4.3 計算性能對比

本文所提算法與對比分析中算法的計算性能對比見表2。

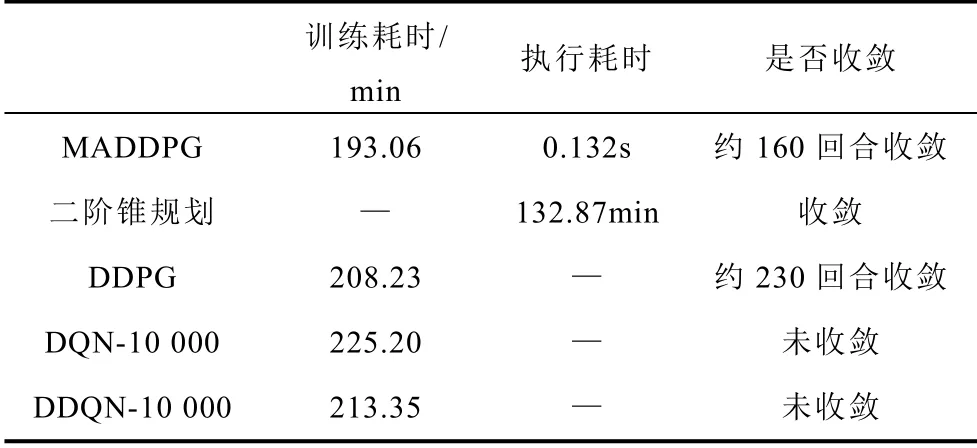
表2 不同算法的性能對比Tab.2 Comparison of algorithms performance

現有有功-無功協調模型主要采用二階錐規劃法。雖然MADDPG 算法的耗時相比二階錐規劃法更長，但本文所提模型是一種“離線訓練，在線執行”的框架，完成訓練后的執行時間較短，為0.132s，而二階錐規劃算法的每一次優化都需要重新計算。同時，采用本文所提方法的優化效果要優于二階錐規劃方法。在強化學習類算法中，本文采用的MADDPG 相比DDPG、DQN 和DDQN 算法在優化效果和計算性能上均具有優勢。

5 結論

1）本文將具有連續狀態空間和連續動作空間的深度強化學習算法引入電力系統有功-無功協調調度領域，構建分層多智能體有功-無功協調調度框架，智能組織靈活多調控資源，使得多個控制主體在最大化自身收益的同時，優化區域內電壓合格率、網損等指標，實現系統各個智能體收益的均衡和各個相沖突的控制目標的協調。

2）改進多智能體深度確定策略梯度算法，設計電力系統多智能體環境、狀態函數、動作函數和獎勵函數，在智能體更新時考慮其他智能體的動作選擇，有效地解決電力系統環境在各智能體動作執行時的不穩定性，顯著提高各智能體訓練效果。

3）與傳統調度模型相比，本文所提模型在均衡智能體收益，協調各智能體動作執行，提高風/光電消納，維持節點電壓穩定，優化網損等方面具有一定的優勢。

4）本文對比了同屬策略迭代類型的DDPG 算法和基于值迭代的DQN 算法和DDQN 算法。對比分析結果表明，本文所用MADDPG 算法在智能體的收斂性能、模型的求解效果和輸出符合規定的調度指令方面具有一定的優勢。

目前，本文針對調度計劃的制定，設計了分層多智能體有功-無功協調調度模型，取得了一定的效果。未來，針對電力系統實時有功-無功協調控制，提高智能體的性能，結合數字仿真，將進一步研究投入數字仿真中的多智能體深度強化學習算法及有功-無功協調控制模型。