渦扇發動機氣路故障的信息融合診斷方法
陶金偉, 王浩楠
(中國航發商用航空發動機有限責任公司,上海 201108)
航空發動機結構復雜、工作環境惡劣、裝配的傳感器數量有限,根據有限的傳感器測量信息診斷發動機部件性能是研究的難點[1]。近年來,發動機健康管理技術(Engine Health Management,EHM)成為當前研究熱點[2],在EHM系統中進行部件故障診斷主要采用以下3種方法:基于物理模型的方法[3](如卡爾曼濾波算法)、基于數據驅動的方法[4](如神經網絡)和基于知識經驗的方法。其中,基于知識經驗的方法過于依賴以往的專家經驗和先驗知識,并不能較好地針對具體工作情況進行準確的診斷,有一定的局限性[5]。基于模型的方法需要精準部件級模型,用于反映真實發動機的物理特性,物理模型的精度對診斷算法的精度影響極大。然而,由于發動機工作環境惡劣且存在大量的不確定因素,故容易因建模誤差導致基于模型診斷算法的漏診甚至誤診。基于數據驅動的方法不依賴于系統模型而只依賴于傳感器搜集到的信息,但算法自身的局限性和測量噪聲等都會對診斷結果造成不利影響[6]。
目前,出現了以各種智能算法為基礎的信息融合技術,如Kuo等[7]采用人工神經網絡(Artificial Neural Networks,ANN)在特征層進行信息融合,完成機器故障診斷。Essawy等[8]提出了一種基于模糊神經網絡的直升機變速箱故障診斷。這類融合能在一定程度上解決單一智能算法存在的缺陷,但是由于沒有考慮到不同發動機的物理特性,片面地從數據出發,一旦發動機的部件特性發生輕微變化或出現新的故障類型,就會嚴重影響部件的診斷精度[9]。因此,眾多研究結合基于模型算法與基于數據驅動算法的特點,如李業波等[10]采用極限學習機(Extreme Learning Machine,ELM)對部件健康參數進行估計,并采用改進迭代約簡最小二乘支持向量回歸機(Improved Recursive Reduced Least Square Support Vector Regression,IRR-LSSVR)算法將基于IDE-ELM(Improved DE-ELM)和基于SVD-Kalman濾波估計的結果在特征層進行融合。由于基于模型算法與基于數據驅動算法的結果互相獨立,當兩者的診斷結果互相沖突時,這就容易導致融合后的結果發生漏診甚至誤診,所以Lu等[11]提出了一種基于量子粒子群尋優(Quantum Particle Swarm Optimization,QPSO)的自調整決策融合機制,通過混淆矩陣計算兩種算法的權值系數,對航空發動機部件性能進行融合診斷。氣路部件融合診斷在全包線內受到基于數據驅動算法的泛化性能的限制,因此需要針對發動機飛行狀態點對基于數據驅動方法計算加權系數。
本文提出一種決策融合算法以EKF與RB-ELM估計得到的部件健康狀況證據體信息為基礎,通過基準值偏差設計概率賦值函數,分別利用混淆矩陣計算基于EKF結果的權值系數,根據飛行狀態點與訓練點距離計算基于RB-ELM結果的權值系數,最后利用D-S證據理論對兩個診斷子系統的決策進行融合,獲得發動機氣路故障融合診斷結果,通過某型渦扇發動機仿真實驗,完成了單個算法、經典D-S合成方法與加權D-S合成方法驗證。
1 故障診斷算法
1.1 EKF算法
擴展卡爾曼濾波(Extend Kalman Filter,EKF)的基本思想是將非線性系統一階近似線性化,再使用線性卡爾曼濾波算法解決問題。EKF是線性卡爾曼濾波算法向非線性系統的延展,該算法在泰勒級數展開中保留了一階導數項,可達到一階近似精度[12]。
對于本文使用的某型雙轉子混合排氣渦扇發動機部件級模型:
(1)
式中,xk=[NL,NH,SE1,SW1,SE2,SW2,SE3,SW3]T為系統狀態變量;k為時間刻度,uk=[Wf,A8]T為系統控制輸入量:zk=[NL,NH,T22,P22,T3,P3,T5,P5]T為傳感器測量值;f(·)和h(·)分別為發動機狀態方程和輸出方程;wk和vk分別為系統互不相關的過程噪聲和測量噪聲,二者均為白噪聲,且滿足wk~N(0,Q2),vk~N(0,R2),其中,Q、R分別為協方差矩陣。具體信息如表1所示。

表1 發動機參數符號示意
EKF算法描述具體如下。
估計:
(2)
更新:
(3)
式中,P為協方差陣;K為卡爾曼增益陣;A、C為雅克比矩陣:
(4)
1.2 RB-ELM算法
將RBM與ELM相結合,可得到RB-ELM算法[13]。在RB-ELM算法中,通過RBM的訓練過程初始化輸入-隱含層參數,改善了ELM隨機生成初始值方式帶來的學習效果不穩定的問題,同時,因為RBM的訓練速度很快,RB-ELM的快速性也有所保障。RB-ELM結構如圖1所示。
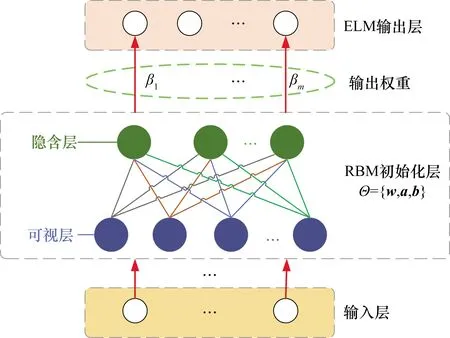
圖1 RB-ELM算法示意圖
RB-ELM的隱含層輸出矩陣較傳統ELM有所不同:
(5)
P(θ;xi)=σ(w·xi+b)
(6)
式中,σ為Sigmoid激活函數。基于RB-ELM的渦扇發動機氣路部件故障診斷包括訓練與測試兩個階段。RB-ELM的訓練過程如圖2所示。

圖2 RB-ELM訓練過程
其中,CD-K算法的參數更新為
(7)
2 融合診斷機制
基于EKF及RB-ELM的加權D-S證據理論的決策融合過程如圖3所示。

圖3 加權D-S合成流程
主要分為以下步驟:
① 構造系統識別框架;
② 基于識別框架的證據體;
③ 針對各證據體,構造各證據體的基本信任分配函數;
④ 計算各證據體的加權系數,進一步生成加權基本信任分配函數;
⑤ 利用D-S證據理論的合成規則得到合成后的基本可信度分配函數;
⑥ 根據合成后的基本可信的分配函數得出診斷結論。
其中,系統的識別框架為Θ={SE1,SW1,SE2,SW2,SE3,SW3,θ},分別為各健康參數,Θ為不確定性。
根據各健康參數偏差可判斷發生故障的部件;各證據體即為分別基于EKF和RB-ELM估計的健康參數結果;根據各估計健康參數與期望輸出的偏差確定基本概率賦值函數;通過混淆矩陣V計算EKF對應的加權系數W1[11],根據飛行狀態點與訓練點間的距離,并根據最小距離計算對應飛行點RB-ELM算法的加權系數W2。加權D-S證據理論合成規則如下:
(8)
(9)
式中,Wmi(A)為加權基本可信度分配函數;m*(A)為加權后的兩個證據融合的基本可信度分配函數;K為加權后的沖突因子,公式為
(10)
3 仿真驗證
在飛行包線內5個訓練點為:H=0 km、Ma=0,H=2 km、Ma=0.8,H=4 km、Ma=1.2,H=8 km、Ma=0.7,H=11 km、Ma=1.1。為了測試融合診斷算法的泛化性能,選取兩個測試點H=2 km、Ma=0.6和H=15 km、Ma=1.5,位置如圖4所示。

圖4 飛行包線內訓練點與測試點的選取
根據部件退化及發生故障的位置,給定10種發動機氣路部件故障模式[12],以及1種無故障模式,如表2。

表2 渦扇發動機的11種健康模式
圖5為100%轉速下兩個子診斷系統在靠近訓練點的測試點1與遠離訓練點的測試點2注入故障模式2的氣路部件健康參數估計結果。

圖5 100%轉速下兩個子診斷系統注入故障模式2的氣路部件健康參數估計結果
從圖5可以看出,在測試點1和測試點2的仿真中,基于EKF估計的SE2都在真實值上下波動,如圖5(a)、圖5(c)所示。但是因為缺少渦輪間傳感器的原因,SE3在仿真時會發生較大的波動,最大偏移量超過1%,從而對診斷結果造成干擾。從圖5(b)可以看出,在靠近訓練點時SE2能按預期變化,且偏移的健康參數與未偏移的健康參數分離度較高,RB-ELM算法在該點的診斷結果具有一定的優越性。在測試點2的仿真結果如圖5(d)所示,RB-ELM的診斷結果中SW2噪聲較大,不能完全反映故障信息,容易造成誤診。
因此,為了克服單診斷算法的局限性,分別對兩個子證據體進行經典D-S理論合成與加權D-S理論合成。在H=15 km、Ma=1.5飛行狀態下,100%相似轉速下分別求取權值系數進行加權融合,在故障模式3和故障模式6下選擇經典D-S融合結果與加權D-S融合結果進行對比,結果如圖6所示。

圖6 測試點2在故障模式3和故障模式6下融合診斷結果
從圖6(a)、圖6(c)可以看出,在高空高馬赫數的情況下,經典D-S融合結果相應性能參數mass函數值分別在0.8和0.7附近波動,可對故障進行診斷。由于RB-ELM估計結果中噪聲較大,導致經典D-S融合結果波動較大,不能完全分離發生偏移的健康參數,可能會有一定的誤診。加權D-S融合結果如圖6(b)、圖6(d)所示,該方法降低了基于數據驅動估計結果的權重,既保證了基于模型方法診斷結果的基本趨勢,同時降低了RB-ELM估計結果中噪聲影響,使偏移健康參數與未偏移的健康參數分離明顯,提高了診斷精度。
4 結束語
本文以擴展卡爾曼濾波算法和受限玻爾茲曼極限學習機算法為基礎,根據兩種算法的估計結果與基準值的偏差構建基本概率賦值函數,兩種算法分別利用混淆矩陣和飛行狀態點與訓練點距離計算權值系數,最后采取D-S理論對兩個子系統的診斷結果進行加權融合,得到系統的故障模式。采取加權D-S融合診斷算法,避免了單獨使用EKF估計時因缺少渦輪間傳感器使結果中高壓渦輪效率發生偏移的問題。同時在遠離訓練點時,降低RB-ELM算法估計結果的權重,從而提高了基于數據驅動算法的泛化性能。通過對渦扇發動機的典型故障模式仿真,驗證了所提出的加權D-S融合診斷算法的有效性,具有較高的診斷精度,該方法可以進一步應用于民用大涵道渦扇發動機的健康預測中。

