基于圖論模型的認知無線電頻譜分配仿真建模研究

劉新浩 馬昕睿 王大為

（山西師范大學物理與信息工程學院，山西 臨汾 041000）

1 引言

無線通信不斷發展壯大，但是目前可以合理分配的頻譜資源較稀缺，對其需求卻不斷提高，頻譜分配資源的短缺已經成為阻礙現代無線通信技術的一個重要問題。然而，有一些科學研究結果表明，傳統的固定式頻譜分配體制，存在著頻譜分配不均，甚至浪費等不良現象，如美國聯邦通信委員會（FCC）的大量調查結果顯示，授權頻譜利用率一般在15%~85%之間[1]。認知無線電技術，可在不對已授權頻段用戶通信造成影響的前提下，實現頻譜分配的動態管理，使非授權用戶機會式地利用游離的授權頻譜資源，使頻譜資源合理利用[2]。本文在圖論模型的基礎上,通過建模仿真提高認知無線電頻譜分配利用率，以得到“頻譜分配”的高效合理利用。

建模中，設置二維頻譜可用矩陣L，其值為0或1，作為非授權用戶n對于m頻譜的可用情況。效益矩陣B為同行列數二維矩陣，其值為正實數，描述非授權用戶在獲得相應頻譜后可得的網絡效益。設置三維矩陣C(M個二維矩陣)，表示用戶在同時使用頻道m時的沖突情況，其值為1表示不同用戶在使用同一信道時會產生干擾。終極頻譜分配的策略將會儲存在無干擾分配矩陣A。本文通過仿真建模將頻譜分配最優化問題抽象成用戶平均效益目標函數求最優解問題，實現頻譜分配的最優化，解決頻譜分配效益低的問題。

2 基于圖論模型的認知無線電的模型建立

2.1 模型主要參數介紹

認知無線電網絡主要由非授權用戶、授權用戶和認知基站共同構成[3]。建造認知基站方便實現了授權與非授權用戶之間的實時通信，在不對授權用戶造成不利影響的情況下，非授權用戶也可以使用該授權頻段，且在實際通信的環境中，授權用戶和非授權用戶均可能會因外界各種因數而發生動態的變化。本文考慮在極短的時間以至于該時間范圍內信道環境保持恒定不變的情況。信道環境參數大致包括效益矩陣B，頻譜可用性矩陣L，干擾分配矩陣C，無干擾分配矩陣A。設置在通信環境中允許可用的頻譜數為M,非授權用戶數量為N，以下對環境參數簡單介紹[4]：

（1）將頻譜效益矩陣B設置為N×M二維矩陣，B={bn,m|bn,m∈R+}N×M，bn,m取正實數，其值可用于表示非授權的用戶n在獲得頻譜m后可以帶來的網絡效益。

（2）頻譜可用性矩陣L同樣為N×M二維矩陣，L={ln,m|ln,m∈{0,1}}N×M，若ln,m=1則認為信道m可對于非授權用戶n使用。

（3）干擾約束矩陣C為用戶在第m個頻段上的沖突情況，設置M個N×N構成的三維矩陣C={cn,k,m|cn,k,m∈{0,1}}N×N×M，在各二維的矩陣中，cn,k,m=1表示授權用戶n和授權用戶k會在同時使用信道m時造成干擾；cn,k,m=0則表示無干擾。

（4）無干擾分配矩陣A也看作N×M的二維矩陣，A被用來保存某時段M個頻譜對N個非授權用戶的最后分配策略，其一般的形式為A={an,m∈{0,1}}N×M，an,m=1表示頻譜m在該時段對n可用。但需特別注意，無干擾分配條件是無干擾分配矩陣才有意義的必要條件。

2.2 解空間的壓縮

頻譜分配最優結果是通過無干擾分配矩陣A進行記錄，對A直接編碼，其中對于維數N×M的編碼難度較高。因A在可用性矩陣L的控制下，值為0的元素所對應A的元素必然為0，因此我們只要從其中提取出值為1的元素實行編碼[5]，優化完成后再按照其相應的關系進行還原。例如圖1，L為4×4二維矩陣，經過簡單地縮減后成為一個1×4一維矩陣X，解的維數由16縮減為4，搜索空間由216降低成24，有效地降低了解空間的復雜度。

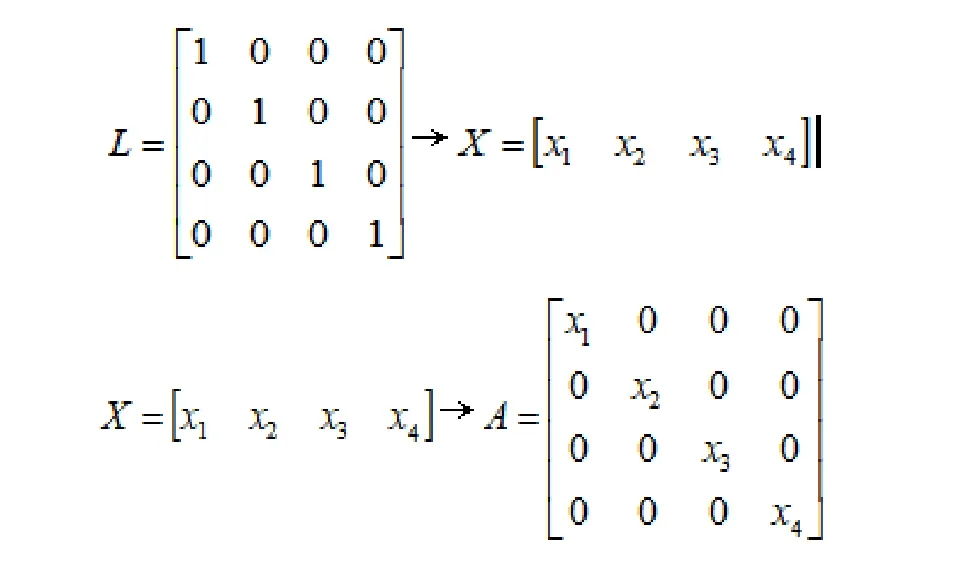
圖1 解縮減實例

2.3 建模算法

無干擾矩陣受可用性矩陣約束，將L中為1的元素提取編碼，優化后根據對應關系還原便可，基于該原理可用設計認知無線電建模算法并縮減其解空間，最終實現頻譜的最優化分配。

基于圖論模型的認知無線電頻譜分配流程圖如圖2所示。

（1）生成可用頻譜矩陣L和干擾約束矩陣C，其中L和C維數已確定，但取值未必合理，故調整保證取值符合要求如圖2所示。

（2）求壓縮后的L，縮減解空間，降低編碼難度如圖3所示。

（3）求壓縮后的干擾約束矩陣C，其中第i列儲存的是和xi不能同時使用同一信道的用戶信息如圖4所示。

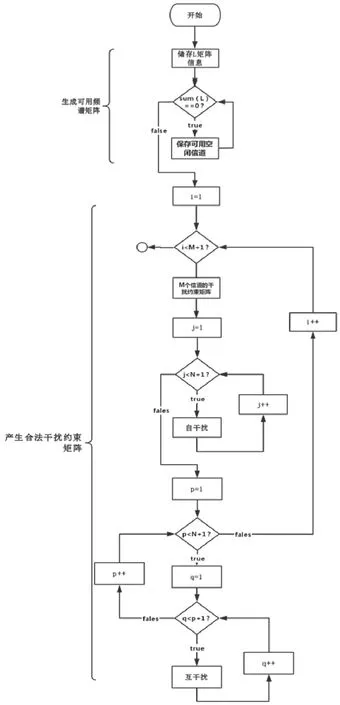
圖2 產生合法L和C

（4）根據縮減后的可用頻譜矩陣，使其對應縮減前對應位置元素1的效益，可得縮減后的效益矩陣B如圖5所示。

得到基于圖論的認知無線電頻譜分配算法如下所示：

%%產生L和C

1返回L矩陣信息

2 while（sum（L）==0）

3生成L矩陣，保證有可用信道

4 end

5 for i=1：M

6生成M個信道的干擾約束矩陣

7 for j=1:N

8 自干擾

9 end

10 for p=1：N

11 for q=1：p

12 互干擾

13 end

14 end

15 end

%%縮減解空間

16保存縮減前后解的映射關系

17確定空間維數

18存放L中1的坐標

19保存縮減后L和原L的映射關系

%%求壓縮后的C

20壓縮后L的頁數

21求壓縮后的L中第i個和第j個元素之間存在的干擾條件

22 if同一個信道可分配給兩個用戶且兩個用戶同時使用該信道會存在干擾

23列數i和每列元素不能同時使用一個信道

%%求壓縮后的效益矩陣

24初始化壓縮效益矩陣

25 for i=1:1：Dim

26儲存L中為1元素對應的效益

27 end

28 end

3 仿真實驗與分析

為探究基于圖論的建模仿真可以優化認知無線電頻譜分配，以提高頻譜利用率。通過建模仿真，對最大網絡總效益和不同認知數和頻道數下平均效益分析研究。其中環境參數L、B、C、M、N設置為：隨機生成的0、1矩陣L；B元素為實數，大小可從1-10隨機選取；C中各二維矩陣是隨機生成的0、1二元對稱矩陣；IBPSO算法參數設置同文獻[6]：種群大小SN=20；c1=c2=4;δ=2，最大的迭代次數設置成1000。

3.1 最大網絡效益比較

假設信道環境在極短時間內不發生改變，頻譜分配可將最大網絡效益作為目標函數。本文以IBPSO算法在圖論模型認知無線電頻譜分配模型下仿真，在分別仿真30次后得到了平均網絡總效益的收斂曲線如圖6所示。

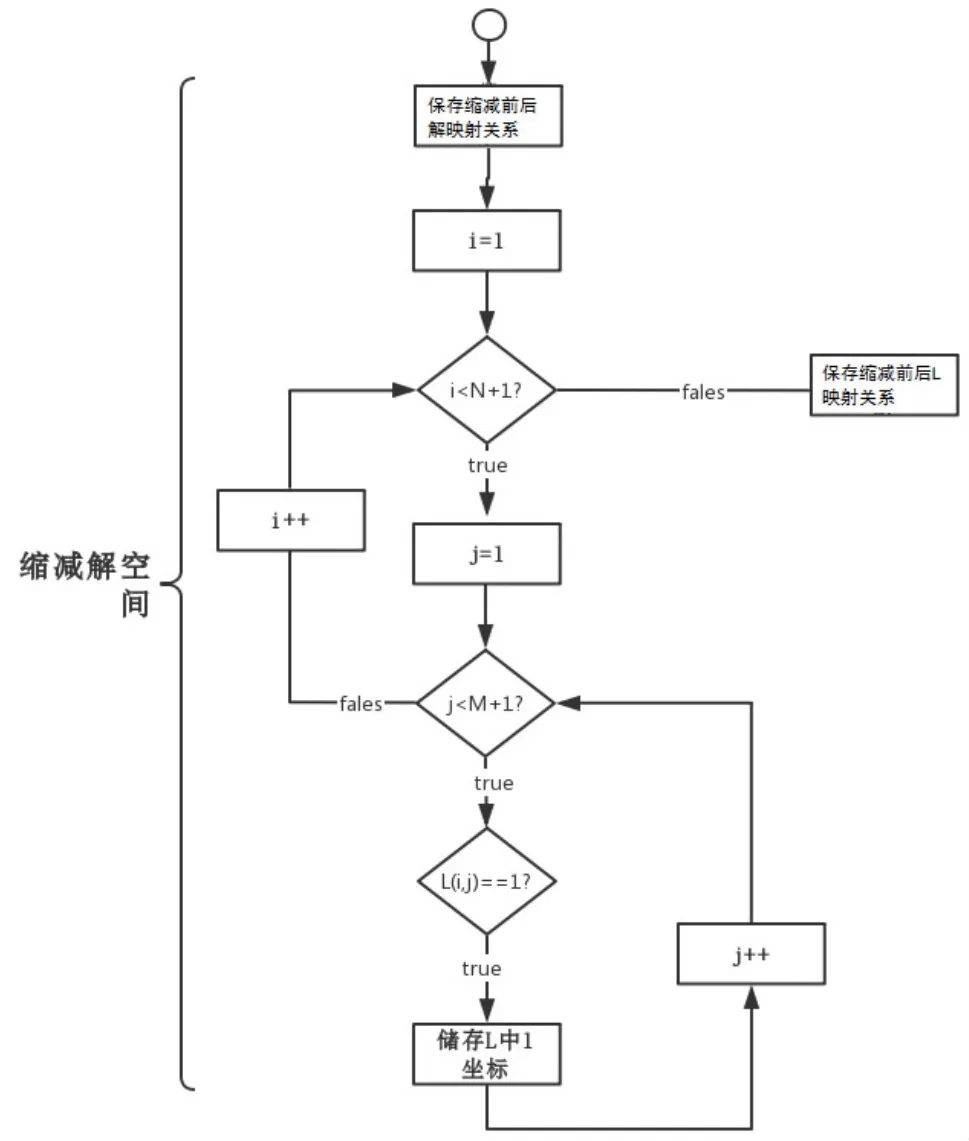
圖3 縮減解空間

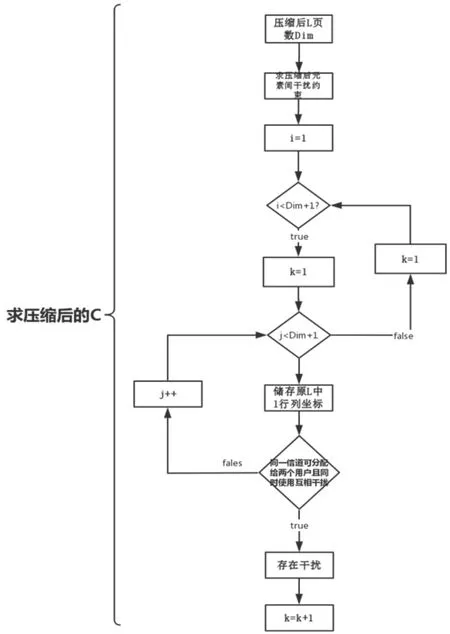
圖4 壓縮后C

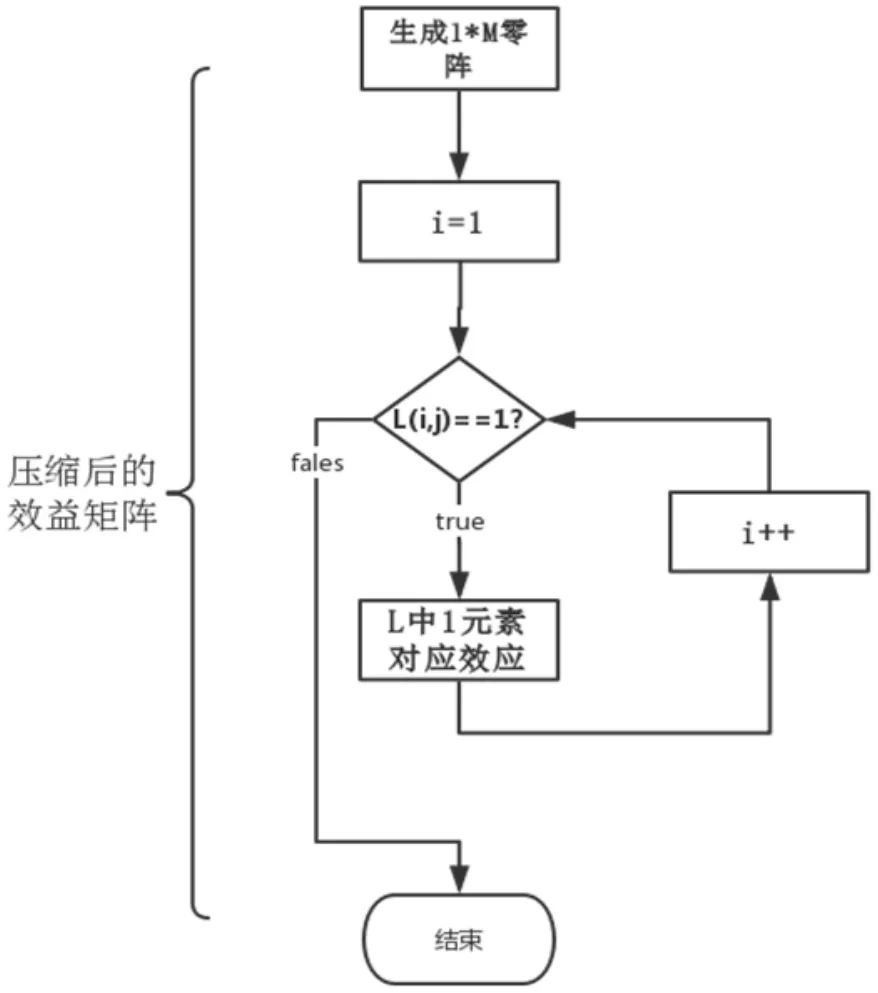
圖5 壓縮后B

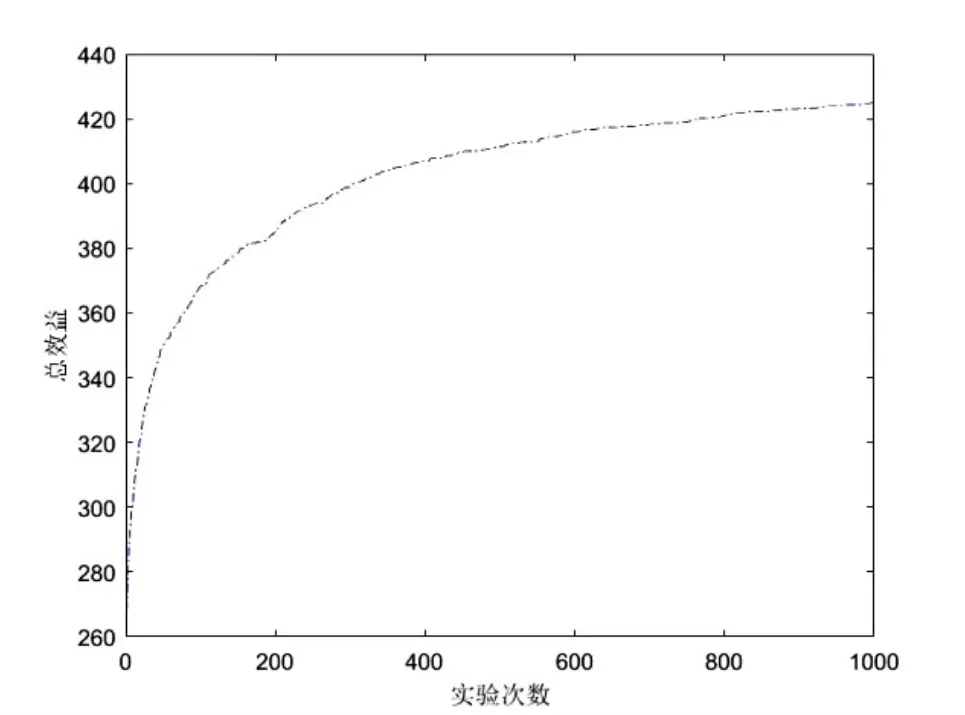
圖6 平均網絡總效益

由IBPSO算法對于平均效益的收斂曲線分析可以清楚地看到，IBPSO算法取得了較好的尋優效果，保證了在進化過程中各個種群的連續性。說明了圖論模型下認知無線電頻譜分配建模可以得到較好的尋優效果。

3.2 不同用戶數下的平均效益

在可用頻譜數M恒定為30，認知數逐漸增加時，仿真得到圖7。可以看出，伴隨認知數增加，平均每個認知用戶所取得的平均效益總體上呈遞減的變化。可見通過圖論模型的無線電建模與實際的頻譜分配時的平均效益相符合。

3.3 不同信道數下的平均效益

設仿真中認知用戶數N恒定為20，可用頻譜M的增加，得到單個用戶獲得的平均效益如圖8所示，可看出伴隨可用頻譜數的逐漸增加，單個用戶已經獲得了較好的平均效益。

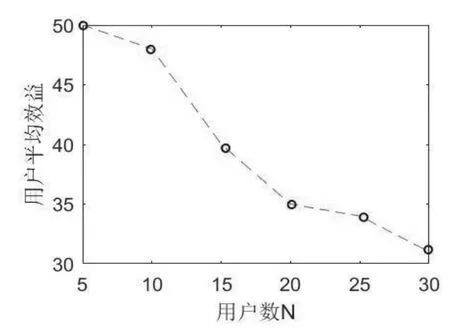
圖7 N增加時的平均效益

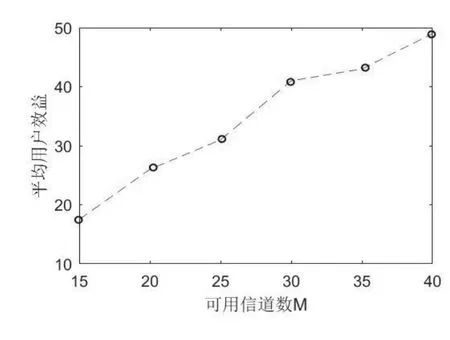
圖8 M遞增時的平均效益

4 結束語

優化頻譜分配，提高頻譜利用率是當前無線通信必須解決的問題之一。頻譜分配模型類似N-Hard約束優化問題[7]，通過圖論模型下的仿真建模可以有效協助解決頻譜分配最優化問題。本文提出了解空間的壓縮方法，可很大程度上降低矩陣編碼難度，大大縮減解空間，還原時只需根據壓縮前對應關系填充即可。在進行仿真實驗與分析時，借鑒IBPSO算法，通過對平均網絡總效益以及在不同的認知用戶數和信道數下的平均效益進行分析，驗證了基于圖論的建模仿真能夠優化認知無線電頻譜分配問題。實驗表明，基于圖論的認知無線電頻譜分配仿真建模研究有利于優化頻譜分配，解決當下頻譜資源緊張問題。