基于密度峰值聚類的大學生異常行為檢測研究
李慧芳 鐘新成 付曉麗
(長治學院計算機系,山西 長治 046011)
1 引言
大學生健康安全成長是高等教育管理者所關注的重點工作。有些大學生因存在掛科、網貸、孤僻等異常行為成為學校的重點關注對象。如何及時發現學生群體中的學生異常行為并進行心理疏導和關懷,已成為高校學生心理健康管理工作的一項重要任務。
目前,常見的異常行為檢測方法包括有監督的異常檢測方法和無監督的異常檢測方法。有監督的檢測方法需要一個事先標記好的訓練集,從而達到訓練分類器識別異常數據的目的。對于異常用戶特別稀少的情形,往往需要大量時間,尋找數據的效率較低。常采用支持向量機、神經網絡等建立檢測模型。無監督的檢測方法不僅不需要提前標記訓練集,在新的異常數據類型出現后,該方法能夠更快更有效率地進行檢測。常采用k-means、近鄰傳播等聚類方法對異常數據進行檢測。這些算法通過對樣本按照相似性分為若干簇,使得屬于同一簇的樣本之間的距離盡可能小而不同簇間的個體間的距離盡可能大[1]。
密度峰值聚類算法于2014年在《Science》上發表,受到了廣大學者的關注[2-4]。目前,已有許多領域采用該算法檢測異常數據特點問題。文獻[5]通過優化初始聚類中心,采用密度峰值聚類檢測算法改善電力大數據異常值的檢測復雜度。文獻[6]通過直方圖均衡化原理優化類間距離,實現密度峰值聚類的短期光伏功率預測。文獻[7]通過密度峰值聚類算法對未知鏈路進行分類,依據分類結果完成鏈路預測。文獻[8]提出一種基于網格的密度峰值聚類方法,該算法的基本思想是采用雙重網格劃分方式對雷達信號脈沖進行實時聚類。實驗結果表明,實時雷達分選聚類很好地處理了雷達信號的重疊嚴重問題。
本文將密度峰值聚類算法應用于大學生異常群體預測,首先采用加權歐式距離應用于樣本點間距離優化,然后建立基于局部密度和高密度距離的決策圖,最后識別正常樣本點與異常樣本點。
2 學生異常檢測算法
2.1 密度峰值距離算法原理
密度峰值聚類算法屬于一種可以發現非凸簇類的無監督學習算法,可以直觀地找到簇數量,也很容易發現異常樣本點。該算法的簇中心具有兩個特點:1)樣本點被相對密度較低的鄰居樣本點所包圍;2)樣本點與更高密度樣本點對象具有相對較大的距離。
為了便于深入分析大學生群體行為,假設學生樣本集X包括m個對象,每個數據對象有n個屬性特征,則X={x1,x2,x3,…,xm},xi=(xi1,xi2,…,xin)。
對樣本點xi的局部密度和高密度距離定義如下:(1)局部密度的定義:

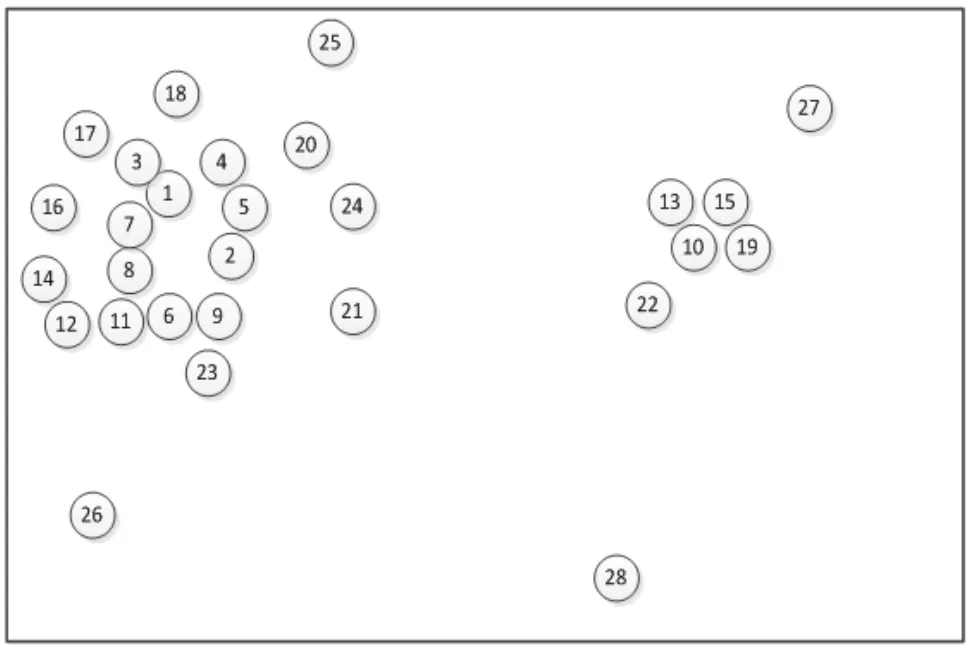
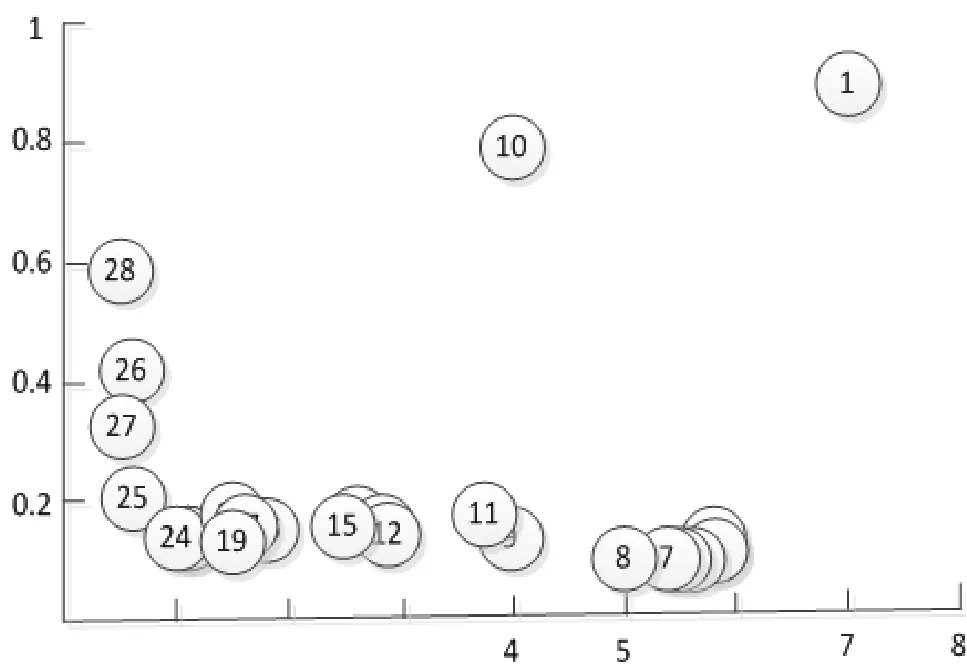
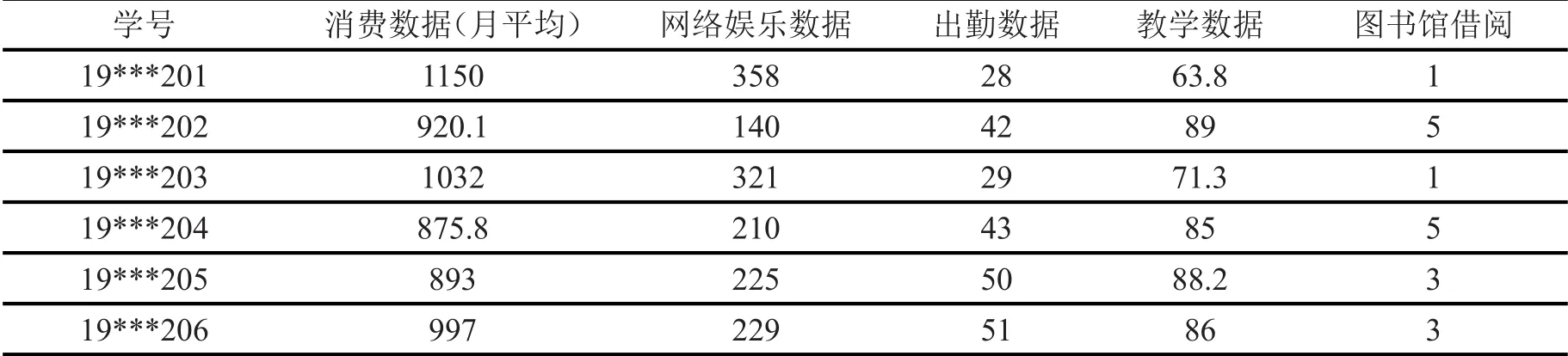
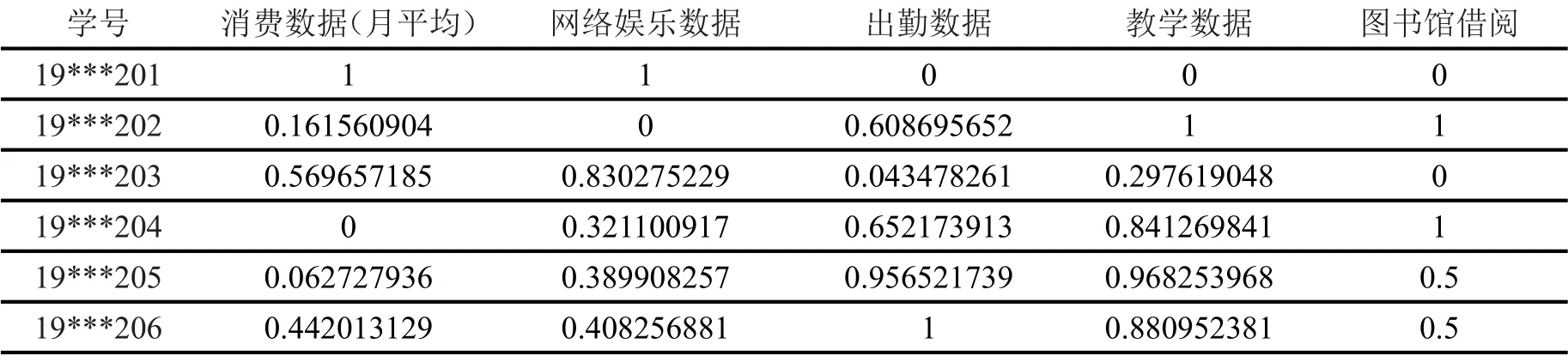
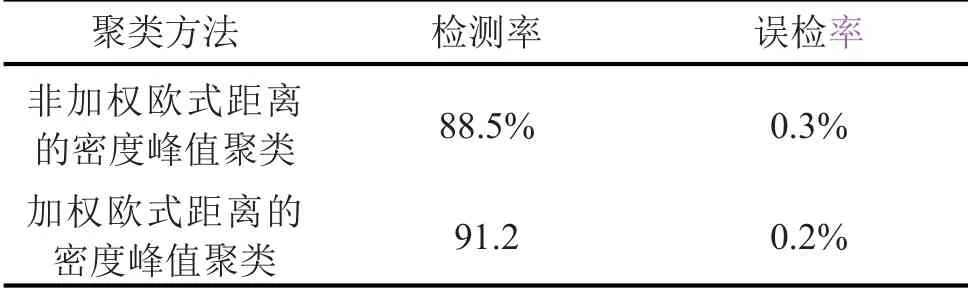
其中i為第i個樣本點,j為第j個樣本點,dij為點xi和xj間的距離,參數d c為截斷距離,φ(x)是分段函數,當dij (2)高密度距離的定義:大于自身局部密度的樣本點中,與離自身最近的樣本點之間的間距。對于任一點xi的高密度距離δi可表示為: 在密度峰值聚類中,距離度量方法會直接影響聚類算法的結果。常見的度量方法有歐式距離和馬氏距離。歐式距離又稱為歐幾里得距離,可以通過樣本之間的距離計算兩個樣本的相似度,距離越近就越相似[9]。在n維空間中,xi和xj間的歐式距離可表示為: 上述的歐式距離公式中樣本點在每個位置的屬性對樣本集的影響認為是均等的,沒有考慮樣本各個維度之間的尺度不一致的問題,會導致判定結果產生誤差。本文提出的屬性加權距離度量方法直接作用到各個維度,將各個維度都滿足標準正態分布。兩個樣本點的加權歐式距離表示為: 其中Sk表示第k維度的標準差。 (1)簇類中心的識別 簇類中心是同時具備較大局部密度和較大高密度距離的樣本點,可表示為: 由簇類中心的定義可知,當樣本點i成為聚類中心點時,其必然具有較大的密度ρ和距離δ,根據上述計算公式,此時樣本點也應具有較大的γ值。該異常檢測算法以局部密度ρ為橫坐標距離δ為縱坐標進行繪制據決策圖。圖1為28個樣本點的分布情況,圖2為依據局部密度和高密度距離都大的樣本點繪制的決策圖。從圖2可以看出樣本點1和樣本點具有較高的局部密度和高密度距離并可以選取為簇類中心。 (2)異常點的識別 為了識別異常點樣本,將屬于某一簇但是距離其他簇不超過d c的樣本點的集合定義為邊界區域,同時將邊界區域中局部密度最高的點定義為ρb。簇中局部密度等于或小于ρb的樣本點分離為異常點。 圖1 樣本點分布 圖2 決策圖 基于密度峰值距離算法的學生異常行為檢測的步驟如下: 輸入:高校學生數據樣本集X={x1,x2,x3,…,xm} 過程: Step1:計算任意兩樣本點之間的距離d ij,構造相似度矩陣。 Step2:將矩陣前1%~2%的值作為截斷距離dc。 Step3:根據公式計算數據樣本集中各個對象的局部密度和高密度距離。 Step4:生成有關的決策圖,標識具有高局部密度和高密度距離的點為簇類中心。 Step5:將非簇類中心分配到最近的高密度簇。 Step6:將局部密度不超過邊界區密度的樣本點視為異常點。 表1 月平均樣本數據(部分) 表2 歸一化后的月平均樣本數據(部分) 輸出:輸出學生樣本集的聚類簇以及學生異常點樣本。 本文所用的驗證數據集均為在長治學院智慧校園系統平臺上采集,將13個系部30個班級共1500名大學生作為觀察對象。采集數據分為消費數據、出勤數據、教學數據、娛樂數據、圖書館借閱數據五大類。消費數據包括學生食堂消費金額、網購快遞次數。出勤數據包括學生運動出勤時間、公益活動時間、社團活動參與時間、食堂寢室時間、圖書館進出次數。教學數據包括課程作業完成情況、課堂參與度、早晚自習、課程成績。網絡娛樂數據包括網絡游戲、網絡追劇。圖書借閱數據包括借閱次數、借閱書籍類型。 樣本集的標準化對實驗結果影響很大,因此在聚類前需要對樣本點進行歸一化處理,使得每個樣本的屬性值轉換為[0,1]之間的數值。 樣本數據如表1所示。 歸一化處理后的樣本數據如表2所示。 為了驗證算法的性能和效果,本文采用未加權的歐式距離密度峰值聚類算法和加權歐式距離的密度峰值聚類算法進行比較,評價指標包括檢測率和誤檢率。檢測率用來表示被正確檢測的異常學生個體占整個異常學生個體的比例。誤檢率用來表示正常學生個體被檢測為異常學生個體數占整個正常學生個體數的比例。實驗結果如表3所示。 表3 各算法聚類檢測率和誤檢率比較 通過對有關班級輔導員和學生代表進行詢問,實驗結果篩選的部分學生異常個體符合對應學生的日常生活和學習行為。部分學生異常個體如表4所示。 表4 部分異常個體 從表3可以分析得出,19***201和19***203兩位學生個體在校園活動記錄較少,該生在圖書館進出次數、運動次數都較少、校園消費金額高、上網時間過長,該生可能存在不經常參加校園活動、作息不規律等行為,可將其認定為異常學生個體。該生輔導員有必要對其學習和生活狀態進行了解,并與其適當進行交流和督促。 本文從高校校園大數據入手,采用密度峰值聚類算法設計并實現了異常學生個體的檢測方法,并在聚類過程中選擇特征加權的距離度量方法。通過實驗證明,本文采用的檢測算法能夠獲得較好的聚類效果和異常識別效果。本文的研究有助于高校管理者充分分析學生行為特點,而且能夠更深層次地挖掘學生異常行為。在今后的工作中,會進一步研究學生屬性之間的關聯對聚類結果的影響。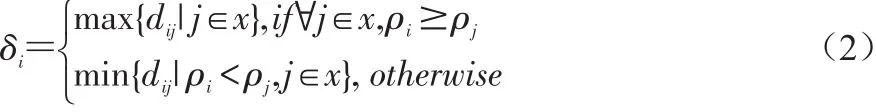
2.2 特征加權的距離度量


2.3 簇類中心和異常點的識別

2.4 算法流程
3 實驗與分析
3.1 實驗數據及預處理
3.2 實驗結果與分析

4 結語

